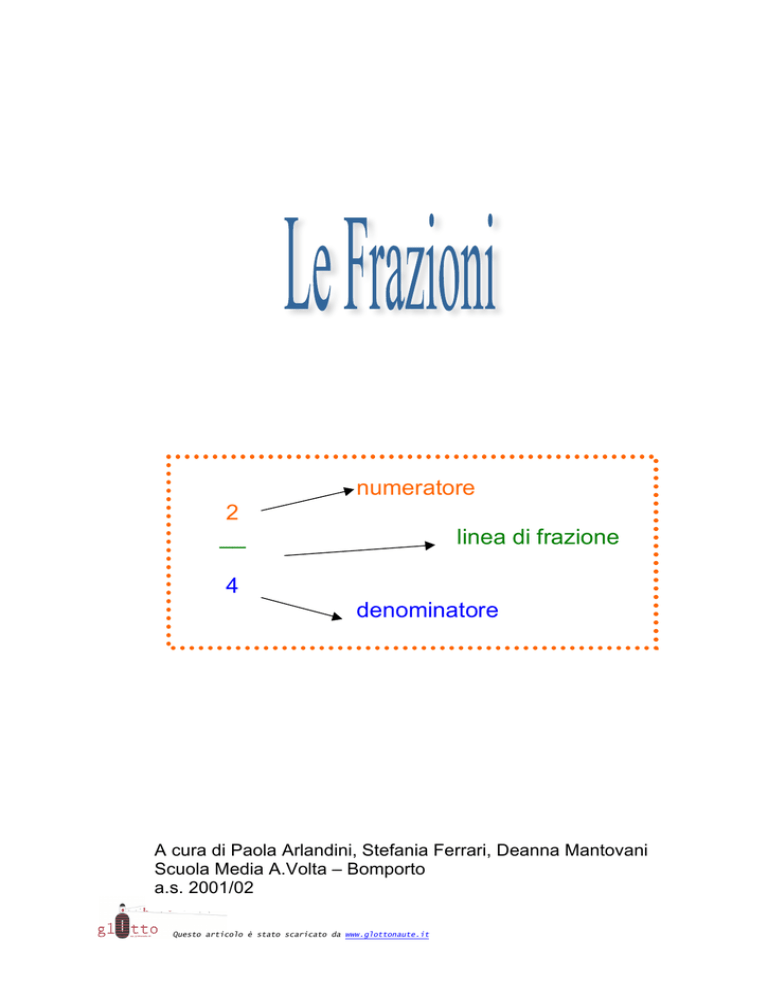
numeratore
2
__
linea di frazione
4
denominatore
A cura di Paola Arlandini, Stefania Ferrari, Deanna Mantovani
Scuola Media A.Volta – Bomporto
a.s. 2001/02
Questo articolo è stato scaricato da www.glottonaute.it
INDICE
Le frazioni, introduzione ………………………………………………p. 3
Le frazioni unitarie …………………………………………………..…p. 6
Scriviamo in simboli frazioni di un segmento …………………….…p. 8
Opero con le frazioni ………………………………………………..…p. 10
Trasformo le frazioni: frazioni e numeri decimali ………………...…p. 13
Frazioni proprie, improprie e apparenti ………………………………p. 16
Frazioni equivalenti ………………………………………………….…p. 19
Proprietà invariantiva …………………………………………………..p. 22
Riepilogo operativo ………………………………………………….…p. 24
Riduco ai minimi termini ……………………………………………..…p. 25
Riduco al minimo comune denominatore ………………………….…p. 29
Addizioni e sottrazioni di frazioni ………………………………………p. 32
Moltiplicazione di frazioni …………………………………………….…p. 38
Divisione di frazioni ……………………………………………………...p. 41
2
2
4
è una frazione. Si legge due quarti
numeratore
2
__
linea di frazione
4
denominatore
ü Prendi un intero
(L’intero può essere un cerchio,
un triangolo, una torta, ecc.)
ü Dividi l’intero in quattro parti uguali
ü Colora due parti
ü La parte colorata è la frazione 2
4
La frazione 2/4 rappresenta 2 delle 4
parti in cui è stato diviso l’intero.
2 è il numeratore della frazione 2/4
4 è il denominatore della frazione 2/4
3
Lavoriamo insieme
Colora una parte , cioè 1 su 4
•
si dice
•
si scrive
un quarto
1 ( è una frazione unitaria )
4
Questo è un intero. Questo intero è diviso in 6 parti:
•
ogni parte è
1
6
dell’intero ( = frazione unitaria )
•
colora due parti, cioè 2 su 6.
si dice due sesti
si scrive
•
2 : ( non è una frazione unitaria)
6
se coloriamo 4 parti, cioè 4 su 6
si dice quattro sesti
si scrive
…….. : questa non è una frazione unitaria
6
Lavoriamo insieme
1. Osserva il disegno e completa:
Ø L’intero è diviso in ………. parti uguali
Ø E’ colorata ……… parte,
cioè …… su ……….
Ø Si dice: un ottavo
Ø Si scrive: ………
2. Osserva il disegno e completa
Ø L’intero è diviso in ….. parti …………..
Ø Ogni parte è ……. dell’intero
Ø Sono colorate 2 parti dell’intero, cioè …… su
…….
Ø I …….. dell’intero sono colorati
Ø Si scrive: …………….
4
3. Colora i 5 della figura A
6
Ø Dividi la figura A in 6 parti uguali
Ø Colora 5 parti
Figura A
Ø La parte non colorata è …… della figura A
5
6
….
4. Colora le parti di autobotte piene di benzina.
Ø La benzina occupa i 2 dell’autobotte
5
Ø La benzina occupa i 3 dell’autobotte
5
Ø L’autobotte è piena di benzina. Un benzinaio
1
compra della benzina. Colora la benzina che
5
rimane.
Esercizi: libro di aritmetica
pag. 355 n. 17-18,
pag. 356 da n.19 a n.25,
pag. 357 dal n. 26 al n. 33
5
Autobotte
Quando il numeratore di una frazione è uguale a uno, la frazione si chiama
frazione unitaria (o unità frazionaria)
Queste sono tutte frazioni unitarie
LE FRAZIONI UNITARIE
1
2
1
3
1
4
1
5
1
6
1
7
1
8
1
9
1
10
1
11
1
12
1
13
1
14
1
15
1
16
Un mezzo
1
17
1
18
1
19
1
20
1
30
1
40
1
50
1
60
1
70
1
80
1
90
1
100
1
200
1
500
1
1000
Un terzo
Un quarto
Un quinto
Un sesto
Un settimo
Un ottavo
Un nono
Un decimo
Un undicesimo
Un dodicesimo
Un tredicesimo
Un quattordicesimo
Un quindicesimo
un sedicesimo
Disegna le frazioni sul quaderno
Esempio
1
6
6
Un diciassettesimo
Un diciottesimo
Un diciannovesimo
Un ventesimo
Un trentesimo
Un quarantesimo
Un cinquantesimo
Un sessantesimo
Un settantesimo
Un ottantesimo
Un novantesimo
Un centesimo
Un duecentesimo
Un cinquecentesimo
Un millesimo
Completa la tabella
Frazione
2
3
3
15
8
9
13
7
2
5
4
19
15
2
1
120
77
24
Numeratore Denominatore
2
3
Scrivi in lettere
7
2
5
3
21
4
18
5
11
6
9
7
3
8
14
9
Sette mezzi
Esercizi:
16
17
23
18
2
19
17
20
1
33
1
45
1
59
1
61
3
100
libro di aritmetica pag. 354
7
Frazione
unitaria
1
3
Scriviamo in simboli frazioni di un segmento
Segui le frecce e disegna i 3 del segmento AB.
5
• il segmento AB rappresenta l’intero
• dividi l’intero in 5 parti uguali
A
B
A
B
1
5
• prendi 3 di tali parti
1
5
1
5
A
B
3
5
• ottieni il segmento AC che è i 3 di AB
5
A
C
• in simboli : AC = 3 . AB
5
STOP
“Il segmento AC è i 3del segmento AB” in simboli si scrive : AC = 3 . AB
3
5
Lavoriamo insieme
Segui le frecce e disegna i 2 del segmento MN.
3
<via
M
Nnnn N N
N
• il segmento MN è l’ ....................
dividi l’intero in ...........uguali
M
N
• ogni parte rappresenta .................
del segmento MN
• colora ........ di tali parti
M
N
Esercizi :
libro di
aritmetica
pag. 358 dal
n° 34 al 45
pag.359 dal n°
52 al 55
• disegna il segmento MO che è i
2 di MN
3
• in simboli : MO = ,,,,,,, MN
8
LAVORIAMO INSIEME.
Dato il segmento AB, disegna il segmento AC che è i 4 di AB
6
a) Dividi AB in 6 parti uguali
A
B
b) Colora 4 di tali parti
A
B
c) Disegna il segmento AC
A
C
AC = ..........AB
DISEGNI
• Dato il segmento AB disegna:
A
a) il segmento AC = 5 . AB
6
B
b) il segmento DE = 3 . AB
6
c) il segmento EF = 2 . AB
3
• Dato il rettangolo A disegna:
d) B = 1 . A
4
A
e) C = 3 . A
8
f)
D=2.A
4
Disegna la figura B che è i 7
10
del rettangolo A
Disegno
A
in simboli :
B = .................. A
in simboli :
B = .................. A
Disegna la figura B che è gli 8
16
del quadrato A
• ottieni ancora un quadrato?
A
Disegno
9
Possiamo calcolare la lunghezza di un segmento AC sapendo che questo e’ i
2
di un altro
3
segmento AB lungo 12 cm.
2
2
Ricorda AC =
di AB, cioè AC = di 12
3
3
:3
significa ( 12 : 3 ) x 2 = 8
oppure 12
x2
4
8
SEGUI L’ESEMPIO
Via
Segui il diagramma di flusso e
Calcola la lunghezza del segmento:
•
AC e’ i 3 del segmento AB [ AB e’ lungo 20 cm.]
5
•
il segmento AB è lungo 20 cm. AB e’ l’intero
•
dividi il segmento AB in 5 parti uguali:
ogni parte è lunga 4 cm; infatti
20 : 5 = 4 ( cm )
•
prendi 3 di tali parti, per cui:
A
20 cm
AC = 4 x 3 = 12 ( cm )
•
3
5
in sintesi: AC = 3 di AB, AB = 20 cm
5
quindi AC = 3 di 20
5
di 20 = ( 20 : 5 ) x 3 = 12 ( cm )
:5
•
oppure
20
12 cm
Stop
x3
4
12 ( cm )
10
Operiamo insieme
Segui il diagramma di flusso,
calcola la lunghezza del segmento AC.
AC e’ i 5 del segmento AB. AB e’ lungo 32 cm.
8
• disegna l’intero. L’intero e’…………….cm.
• dividi l’intero in ……………parti uguali
Ogni parte ha la lunghezza di ………………cm
Infatti :………………=……………………..cm
• prendi solo…………………..
parti
5
AC =
x 32 =………………………( cm )
8
32 cm.
STOP
• Determina la lunghezza del
7
segmento AC. AC e’ i
del
10
segmento AB.
•
•
•
•
•
AB e’ lungo 100 cm.
La lunghezza dell’intero
AB e’ ……………..cm
In quante parti uguali devi dividere il
segmento?……………………….
……………………………..
La lunghezza di ogni
parte e’
……………………………
Quante parti
prendi?………………………….
La lunghezza del segmento
A
B
……………………………..
………………………………
AC e’…………………….
………………………………
7
x 100 =……………..( cm)
10
• In sintesi:
…..
oppure
100
11
……
……
……=……( cm)
PROVA TU E VERIFICA
Il segmento AB e’ lungo 16 cm,
determina la lunghezza del segmento
AC sapendo che il segmento:
5
• AC e’ i di AB
4
A
AC = ………………………….
• AC e’ i 7 di AB
8
AC = ……………………….
B
• AC e’ i 16 di AB
16
AC =…………………….
Determina la lunghezza del segmento AC, sapendo che e’ i 3 del segmento AB. AB e’ lungo 28
cm.
7
3
• Il problema chiede di determinare i
di 28 cm
7
7 x
• La soluzione e’ 28 :
:7
Oppure : 28
cm.
3
= ……………………..( cm)
x3
4
12 ( cm ). La risposta e’ allora : il segmento AC e’ lungo 12
ESERCIZI PAG. 359 N0 46, 47, 48, 49,50, 51,
12
0, 1, 2, 4, 5, 6, 7, … eccetera sono numeri naturali
0,325 è un numero decimale finito (< 1)
0,7777777….. è un numero decimale infinito (< 1)
(cioè il 7 si ripete all’infinito)
Ricorda: La divisione
10
:
dividendo
5
=
divisore
2
quoziente
Maggiore: >
5>1
5 è maggiore di 1
Minore <
3 < 10
3 è minore di 10
Uguale =
5=5
5 è uguale a 5
10 = 10:5 = 2
5
il quoziente della frazione è un numero naturale
5 = 5:2 = 2,5
2
il quoziente della frazione è un numero decimale finito
2 = 2: 3 = 0, 6666666
3
il quoziente della frazione è un numero decimale infinito
Una frazione può diventare un numero naturale o un numero decimale
13
1. Guarda l’esempio e completa la tabella
La frazione
a = (b ≠ 0)
b
m =m:n
n
Il quoziente è un
numero naturale o un
numero decimale?
Il quoziente è
>, < , = 1
2
3
2 = 2:3 = 0,66666… 0,666666… < 1
3
1
2
1 = 1:2 = ………
2
…………….
1
6
2
6 = 6:2 = …………
2
…………….
1
3
4
3 = ……… = ………
4
…………….
1
2
9
2 = ……….= ………
9
…………….
1
50
6
50 = ………=………
6
…………….
1
2. Segui gli esempi e completa la tabella
Dalla divisione
a: b
Al quoziente
a
b
7:2
7
2
20 : 4
………….
8:2
…………
3:7
………….
11 : 4
…………...
13 : 8
…………...
c:d
…………..
14
Decimale
………………………….
………………………….
………………………….
………………………….
………………………….
Ø Trasforma le frazioni in numeri naturali
decimali
7 = 7 : 11 = 0,63636…
Esempio:
11
0 = ………
8
9 = 9:11 = 0, 8181818…
11
100 = ……….
100
9 = ………
11
8 = ………..
5
3 = ………..
2
9 = ……….
17
15 = ……….
7
11:7 = 11
7
60:2 =
18:2 =
21:6 =
Ø Trasforma le divisioni in frazioni
19 : 7 =
11 : 2 =
14 : 7 =
1: 4 =
5: 9 =
15
27 : 9 =
Ø Se il numeratore è minore del denominatore, la frazione è propria
Esempio:
3
7
, 3 < 7, numeratore < denominatore = FRAZIONE PROPRIA
Ø Se il numeratore è maggiore o uguale al denominatore, la frazione è impropria
Esempio:
19 , 19 > 3, numeratore > denominatore = FRAZIONE IMPROPRIA
3
Ø Se il numeratore è multiplo del denominatore la frazione è impropria apparente
Esempio:
8 , 8 è multiplo di 4 (4 x 2 = 8) = FRAZIONE IMPROPRIA APPARENTE
4
Guarda l’esempio:
Data una frazione n , dove
d
Scopri se la frazione è
n = numeratore
d = denominatore
PROPRIA
IMPROPRIA
APPARENTE
Frazione propria, impropria o apparente?
1
Frazione propria
2
16
4
5
9
1
3
25
5
n<d
n>d
n multiplo di d
Frazione propria, impropria o apparente?
8
64
17
3
18
19
1
4
81
3
16
Segui l’esempio
Data una frazione n dove n e’ il
d
numeratore e d il denominatore,
N
D
numeratore
n
d
5
7
denominatore
5
7
3
2
3
2
Impropria
10
5
10
5
Apparente
scopri se la frazione e’
•
•
•
Propria
Impropria
apparente
Propria
Ricorda
frazione impropria
frazione apparente
frazione propria
• Se il numeratore n e’ minore del • Se il numeratore n e’ maggiore o • Se il numeratore n e’ diverso da
uguale al denominatore d, allora
0 e multiplo del denominatore d
denominatore d allora la frazione
e’ una frazione impropria
allora la frazione e’ apparente
e’ propria. ES. n = 5
ES.
n
=
3
3
>
2
es.
n
= 10 10 multiplo
d 7
d 2
d 5 di 5
Operiamo insieme
Completa la tabella e scrivi se
la frazione e’
Propria
Impropria
Apparente
…………….
3
n
d
2
3
7
……………
7
2
0
7
1
……………
1
1
12
3
……….
3
4
N
numeratore
D
denominatore
A,B,C
•
Propria
•
Impropria
……………. •
Apparente
…………………
………………….
……………. ………………….
Se trasformi la frazione in divisione e calcoli il quoziente puoi dire se una frazione e’ propria,
impropria o apparente.
17
Segui l’esempio e operiamo insieme
Indica con una crocetta se e’ una frazione propria, impropria o apparente.
n
n =n:d
Il quoziente e’ < 1 Il quoziente e’> 1 Il quoziente e’ un
d
d
frazione propria
frazione impropria numero naturale
±0
frazione apparente
4
4 : 5 = 0,75 < 1
…propria……..
…………………. ………………….
5
10
2
10 : 2 = 5 > 1
…………………. …………………. ………………….
11
2
11 : 2 = …….< 1
…………………. …………………. ………………….
5
1
………
………. …………………. …………………. ………………….
7
12
………
………. …………………. …………………. ………………….
Prova tu e verifica
•
Quali frazioni sono proprie, improprie,
apparenti?
•
Quali frazioni sono proprie , improprie,
apparenti?
Rispondi dopo aver calcolato il quoziente
a) 7 e’ una frazione…………….
11
b) 26 e’ una frazione…………….
13
c) 13 e’ una frazione…………….
12
d) 4 = 4 : 25 e’ una frazione…………….
25
e) 18 = 18 : 6 e’ una frazione…………….
16
2 è una frazione propria : numeratore < denominatore 2 < 3 ; 2 : 3 = ……
3
• 3 è una frazione impropria : numeratore > denominatore 3 > 2, 3 : 2 = 1,5 >1
2
• 6 è una frazione apparente : 6 è multiplo di 2
2
(≠ 0 ) ; 6 : 2 = 3 ∈ N
•
Es.61 pag. 360 ; pag 361 no 62- 73- 74- 75- 76 ; pag. 362 no 78- 79- 80-84
18
Due frazioni sono equivalenti se hanno lo stesso valore.
Es. 2 = 2 : 3 = 0,666666.... ;
3
2
3
e
4
6
4 = 4 : 6 = 0,666666......
6
hanno lo stesso valore, quindi sono equivalenti
Dato un segmento AB :
A
B
• disegna CD = 2 AB
3
A
C
B
• ora disegna EF = 4 AB
6
A
E
F
• Confronta
C
E
D
F
CD e EF
D
B
Se CD = EF le due frazioni 2 e 4 sono equivalenti.
3
6
Dato il numero 50:
• calcola i 2 di 50
5
50 : 5 x 2 = 20
• ora calcola i 4 di 50
10
50 : 10 x 4 = 20
• confronta i due risultati
20 = 20
Se i due risultati sono uguali allora le due frazioni 2 e 4 sono equivalenti.
5
10
19
LAVORIAMO INSIEME
1)
Dato un segmento AB :
A
B
• disegna CD = 1 AB
2
A
C
B
D
• ora disegna EF =2 AB
4
A
E
F
• Confronta
C
E
D
F
CD e EF
B
• le due frazioni sono equivalenti ? ..............................
• allora puoi scrivere ..................................................................
2) Dato il numero 100 :
• calcola i 3 di 100
4
• calcola i 15 di 100
20
• confronta i due risultati
Le due frazioni sono equivalenti ?
3) Dato il numero 70 :
• calcola i 70 di 70
10
• ora calcola i 10 di 70
70
• confronta i due risultati
Le due frazioni sono equivalenti ?
....................=..............
....................=..............
...........................
..........................
....................=..............
....................=..............
...........................
..........................
20
esegui
gli
esercizi
Segna con una crocetta le coppie di frazioni equivalenti.
1) A
C
B
D
E
F
4 e 2
10
5
CD = 4 AB
10
EF = 2 AB
5
2) 7 di 21 = 21 : 3 x 7 = 49
3
7 e 14
3
7
14 di 21 = 21 : 7 x 14 = 42
7
3) 13 di 12 = 12 : 2 x 13 = 78
2
13 e 26
2
4
26 di 12 = 12 : 4 x 26 = 78
4
4) 4 di 20 = 20 : 5 x 4 = 16
5
4 e 5
5
4
5 di 20 = 20 : 4 x 5 = 25
4
Esercizi
pag. 365 n° 119; pag. 366 n° 120 - 121
21
Quando moltiplichiamo o dividiamo il numeratore ed il denominatore per uno stesso numero
troviamo una frazione equivalente
Segui l’esempio
4_
10
Data la frazione:
X
•
Se moltiplico ( o divido) il numeratore
e il denominatore per uno stesso numero
ottengo una frazione a essa equivalente
4
______
10
=
X
•
Oppure piu’ sinteticamente:
3
:2
12
_____
30
;
4
___
10
3
=
2
____
5
:2
4
4x 3
12
___ = ______ = ____
10
10 x 3
30
4
4 : 2
2
____ = _____ = __
10
10 : 2
5
Operiamo insieme
20
___
12
Data la frazione:
X
•
Scrivi una frazione equivalente
a) moltiplica numeratore e denominatore per 4
b) dividi numeratore
e denominatore per 2
20
______
12
=
X
•
Oppure piu’ sinteticamente:
4
:2
…..
_____ ;
……
4
20
20 x … …..
___ = ______ = ____
12
12 x … …..
22
20
___
12
=
.….
____
…..
:2
20
20 : … ...
____ = _______ = __
12
12 : …
…
Prova tu e verifica
a)= …x 10…
b)=……….
c) = ………..
7
__ =
10
25
5
___ = ___
75
15
88
8
___ = _____
11
Scrivi l’operazione mediante
la quale si e’ passati
dalla prima frazione a quella equivalente
70
____
100
…….
50
Data la frazione __
12
:2
50
….
___ = ____
12
…..
:2
Esercizi :
I gruppo
4 =
15
8
5
16
24
15
60
4 x4
15 x 4
=
8x…
5x 3
=
16 : 4
24: …
=
=
………
……..
=
………
………
15 : ….. =
60 :……
………
……...
II gruppo
………
1
3
=
=
3
10
=
3 x5
10 x…..
=
………
2
7
=
2 x ….
7 x ….
=
………
………
42
30
=
42 : …
30 : 6
15
18
=
15 : …..=
18 :….
………
4
12
5
7
……..
………
8
20
x3
………
=
=
12
30
15
21
=
……..
……..
=
………
………
………
………
………
6
15
……..
………
4
10
………..
x3
25
___ =
…..
sono sicuramente equivalenti :
…….
=
……..
………
2
5
21
14
=
……..
Esercizi pag 366 dal N0 122 al 130
23
12
30
3
2
1)
a) Colora i 4 di AB
5
b) Colora i 3 del rettangolo A
5
A
B
A
2) Trova i 7 di 330
11
..........................................................
3) Trova i 2 del segmento AB lungo 105
cm
...............................................................
4)
a) Scrivi una frazione che genera un
numero naturale > 1
b) Scrivi una frazione che genera un
numero naturale < 1
c) Scrivi una frazione che genera il
numero naturale 2
....................................
....................................
.....................................
5)
a) Completa in modo che tutte le frazioni
siano proprie
1
...
2
...
3
...
.....
4
.....
5
.....
6
b) Completa in modo che le frazioni siano
improprie ma non apparenti
1
...
2
...
3
...
.....
4
.....
5
.....
6
c) Completa in modo che le frazioni siano
improprie apparenti
1
...
2
...
3
...
.....
4
.....
5
.....
6
6)
a) Scrivi tre frazioni equivalenti
3 = ...... = ...... = ......
7 ...... ...... ......
b)Scrivi tre frazioni equivalenti
(dividi numeratore e denominatore per uno 100 = ...... = ...... = ......
stesso numero)
40
...... ...... ......
7) Riduci le seguenti frazioni ai minimi
termini
8) Di ogni frazione scrivi una frazione
equivalente
13 = ...... ;
26 .....
50 = ...... ;
20 .......
7 = ...... ;
11
66
3 = ...... ;
9
54
24
38 = ......
48 ......
3 = ......
15
60
Posso ridurre una frazione solo se posso dividere il numeratore e il denominatore di una frazione per lo stesso
numero.
1) Riduci la frazione 24 ai minimi termini
18
• Il numeratore 24 e il denominatore 18 si possono dividere per 2
24 : 2 = 12
18 : 2
9
•
Ora 12 e 9 si possono dividere per 3
12 : 3 = 4
9:3
3
•
4 e 3 si possono dividere solo per 1. Si dice che 4 e 3 sono numeri primi tra loro.
Quando numeratore e denominatore sono numeri primi tra loro, si dice che la frazione è ridotta ai minimi
termini
RICORDA: Una frazione è ridotta ai minimi termini quando il numeratore e il denominatore sono numeri primi,
cioè quando il numeratore e il denominatore si possono dividere solo per 1
2) Riduci la frazione 72 ai minimi termini
120
• Il numeratore 72 e il denominatore 120 si possono dividere per 2
72 : 2 = 36
120 : 2 60
oppure: Il numeratore 72 e il denominatore 120 si possono dividere per 2.
72: 2 = 36, cancello 72 e scrivo 36
120: 2 = 60, cancello 120 e scrivo 60
36
72
120
60
•
Ora 36 e 60 si possono dividere ancora per 2
36 : 2 = 18
60 : 2
30
oppure: Il numeratore 36 e il denominatore 60 si possono ancora dividere per 2.
36: 2 = 18, cancello 36 e scrivo 18
60: 2 = 30, cancello 60 e scrivo 30
18
36
72
120
60
30
•
Il numeratore 18 e il denominatore 30 si possono dividere per 2
18 : 2 = 9
30 : 2 15
oppure: Il numeratore 18 e il denominatore 30 si possono
ancora dividere per 2.
18: 2 = 9, cancello 18 e scrivo 9
30: 2 = 15, cancello 30 e scrivo 15
9
18
36
72
120
60
30
15
25
•
Ora 9 e 15 si possono dividere per 3
9:3 =3
15 : 3
5
oppure: Il numeratore 9 e il denominatore 15 si possono dividere per 3.
9 : 3 = 3, cancello 9 e scrivo 3
15 : 3 = 5, cancello 15 e scrivo 5
3
9
18
36
72
120
60
30
15
5
•
3 e 5 si possono dividere solo per 1.
Si dice che 3 e 5 sono numeri primi tra loro.
Quando numeratore e denominatore sono numeri primi tra loro, si dice che la frazione è ridotta ai minimi
termini
•
La frazione 72 ridotta ai minimi termini diventa 3
120
5
26
3) Riduci la frazione 20 ai minimi termini
60
•
Il numeratore 20 e il denominatore 60 si possono dividere per 2.
20: 2 =……, cancello 20 e scrivo …….
60 : 2 =……, cancello 60 e scrivo …….
…..
20
60
…..
•
Ora 10 e 30 si possono dividere ancora per 2
10: 2 = ……, cancello ….. e scrivo …..
30: 2 = ……., cancello ….. e scrivo …..
…..
10
20
60
30
…..
•
Il numeratore 5 e il denominatore 15 si possono dividere per 5
5 : 5 = ….., cancello ….. e scrivo …..
15 : 5 = ….., cancello …… e scrivo …..
…..
5
10
20
60
30
15
…..
•
1 e 3 si possono dividere solo per 1.
Si dice che …… e …… sono numeri primi tra loro.
Quando numeratore e denominatore sono numeri primi tra loro, si dice che la frazione è ridotta ai minimi
termini
•
La frazione 20 ridotta ai minimi termini diventa …….
60
……..
27
4) Riduci la frazione 24 ai minimi termini
36
•
Il numeratore 24 e il denominatore 36 si possono dividere per 2.
24: 2 =……, cancello ….. e scrivo …….
36 : 2 =……, cancello ….. e scrivo …….
•
Ora …… e …… si possono dividere ancora per ……
……: …… = ……, cancello ….. e scrivo …..
…… : …… = ……., cancello ….. e scrivo …..
•
•
Il numeratore …… e il denominatore …… si
possono dividere per ……
….. : …… = ….., cancello ….. e scrivo …..
….. : …… = ….., cancello …… e scrivo …..
…..
…..
…..
….. e …… si possono dividere solo per 1.
Si dice che …… e …… sono numeri primi
tra loro.
La frazione 24 ridotta ai minimi termini diventa
36
Esercizio:
Riduci queste frazioni ai minimi termini
a.
30
45
b.
44
33
c.
66
49
d.
100
350
……
24
36
Quando numeratore e denominatore
sono numeri primi tra loro, si dice che
la frazione è ridotta ai minimi termini
•
…..
……
Esercizi dal libro: pag. 367 dal n° 150 al n° 153
28
…….
…..
Riduci due frazioni al minimo comune denominatore, cioè trasforma due frazioni ridotte ai minimi termini in due
frazioni con lo stesso denominatore
1)
Riduci due frazioni al minimo comune denominatore, cioè trasforma le due frazioni
il denominatore uguale
•
Trova il m.c.m. tra i denominatori 2 e 15
m. c. m. (2;15) = …..
q
Trova i primi 10 multipli di 2 e 15
Cerchia i multipli comuni
M2
2; …; 10; …; …; … ; …; … ; …; …
M15
15; …; ….. ; …; …; … ; …; … ; …; …
q
Prendi il più piccolo
Il multiplo più piccolo di 2 e 15 è 30.
q
Il multiplo più piccolo di due numeri è il minimo comune multiplo
m. c. m (…; …) = …
•
Trasforma
1 2
in frazioni con denominatore uguale al m. c. m. 30
2 15
1 ?
=
2 30
1 .....
=
2 30
q Dividi
q
30 per il denominatore 2
30:2 = 15
Moltiplica il risultato 15 per il numeratore 1
15 x 1 = 15
x 15
q
1 15
=
2 30
:
29
1 2
in frazioni con
2 15
2
?
=
15 30
2 .....
=
15 30
q Dividi
30 per il denominatore 15
30:15 = ……
q Moltiplica
il risultato …… per il numeratore 2
….. x 2 = ……
x …...
q
2
4
=
15 30
:
2)
Riduci due frazioni al minimo comune denominatore, cioè trasforma le due frazioni
il denominatore uguale
• Trova il m.c.m. tra i denominatori 5 e 8
m. c. m. (5;8) = …..
3 7
in frazioni con denominatore uguale al m. c. m. 40
5 8
3 ?
=
5 40
• Trasforma
q
x ……
3 .....
=
5 40
:
q
7
?
=
8 40
x ……
7 .....
=
8 40
:
30
3 7
in frazioni con
5 8
3)
Riduci due frazioni al minimo comune denominatore, cioè trasforma le due frazioni
con il denominatore uguale
• Trova il m.c.m. tra i denominatori 16 e ……
m. c. m. (16;…..) = …..
• Trasforma
17 81
in frazioni con denominatore uguale al m. c. m. ……
16 4
x ……
x ……
17 .....
=
.16 ......
81 .....
=
4 ......
:
4)
17 81
in frazioni
16 4
:
Riduci due frazioni al minimo comune denominatore, cioè trasforma le due frazioni
5 4
in frazioni con
3 7
il denominatore uguale
• Trova il m.c.m. tra i denominatori 3 e ……
m. c. m. (3;…..) = …..
• Trasforma
5 4
in frazioni con denominatore uguale al m. c. m. ……
3 7
x ……
x ……
5 .....
=
.3 ......
4 .....
=
7 ......
:
5)
:
Riduci due frazioni al minimo comune denominatore le due frazioni
10 19
21 3
• Trova il m.c.m. tra i denominatori ….. e ……
m. c. m. (…..;…..) = …..
• Trasforma
10 19
in frazioni con denominatore uguale al m. c. m. ……
21 3
x ……
x ……
10 .....
=
21 ......
19 .....
=
3 ......
:
6)
:
Riduci le frazioni al minimo comune denominatore
3 1
;
4 6
5 1
;
9 3
7 1
;
12 6
2 7
;
11 33
31
ADDIZIONE DI FRAZIONI CON DENOMINATORE UGUALE
1) Calcola:
2 4
+ =
9 9
•
Colora di rosso i
•
Colora di blu i
•
2
dell’intero
9
4
dell’intero
9
2
2 4 2+4 6 6 2
+ =
= = =
9 9
9
9 9 3
2
9
4
9
3
2) Calcola:
5 1
+ =
8 8
5
dell’intero
8
•
Colora di rosso i
•
Colora di blu
•
5 1 ..... + ..... 6 ..... .....
+ =
= =
=
8 8
8
8 ..... .....
......
......
1
dell’intero
8
……
.....
.....
…..
3) Calcola:
3 2
+ =
5 5
3
dell’intero
5
•
Colora di rosso i
•
Colora di blu
•
3 2 ..... + ..... ..... .....
+ =
=
=
= ......
5 5
......
...... .....
......
......
2
dell’intero
5
32
.....
.....
SOTTRAZIONE DI FRAZIONI CON DENOMINATORE UGUALE
1) Calcola:
7 2
− =
9 9
7
dell’intero
9
•
Colora di rosso i
•
Colora di blu i
•
7 2 7−2 5
− =
= =
9 9
9
9
2
dell’intero
9
5
9
2) Calcola:
5 1
− =
6 6
•
•
•
......
dell’intero
.....
.....
Colora di blu i
dell’intero
.....
..... ..... ...... − .....
−
=
=
..... ......
......
Colora di rosso i
3) Calcola:
6 4
− =
7 7
•
•
•
......
dell’intero
.....
.....
Colora di blu i
dell’intero
.....
..... ..... ...... − .....
−
=
=
..... ......
......
Colora di rosso i
Esercizi dal libro pag.375 dal 43 al 47
Pag. 376 – 377 dal n° 83 al n° 86
33
ADDIZIONE E SOTTRAZIONE
DI FRAZIONI CON DENOMINATORI DIVERSI
Per sommare o sottrarre due frazioni che hanno i denominatori diversi, devo prima ridurre le frazioni al minimo
comune denominatore
1) Calcola
•
5 3
+ =
4 7
5 3
; al minimo comune denominatore
4 7
Prima riduci le due frazioni
q
Trova il m.c.m. tra i denominatori 4 e 7
m. c. m. (…..;…..) = …..
q
Trasforma
5 3
; in frazioni con denominatore uguale al m. c. m. ……
4 7
x ……
x ……
5 .....
=
4 ......
3 .....
=
7 ......
:
•
:
Poi somma le due frazioni
5 3
;
4 7
5 3
+ =
4 7
5 35
=
4 28
3 12
=
7 28
5 3 35 12 35 + 12 47
+ =
+
=
=
4 7 28 28
28
28
2) Calcola
•
3 1
− =
4 5
Prima riduci le due frazioni
3 1
; al minimo comune denominatore
4 5
q
Trova il m.c.m. tra i denominatori 4 e …..
m. c. m. (…..;…..) = …..
q
Trasforma
3 1
;
4 5
in frazioni con denominatore uguale al m. c. m. ……
x ……
x ……
3 .....
=
4 ......
1 .....
=
5 ......
:
:
34
•
Poi sottrai le due frazioni
3 1
;
4 5
3 1
− =
4 5
3 ......
=
4 .....
1 .....
=
5 .....
3 1 ...... ..... ..... + ..... ......
− =
+
=
=
4 5 ..... ......
.....
......
3) Calcola
•
7 9
+ =
2 11
7 9
; al minimo comune denominatore
2 11
Prima riduci le due frazioni
q
Trova il m.c.m. tra i denominatori ….. e …..
m. c. m. (…..;…..) = …..
q
Trasforma
7 9
in frazioni con denominatore uguale al m. c. m. ……
;
2 11
x ……
x ……
7 .....
=
2 ......
9 .....
=
11 ......
:
•
Poi somma le due frazioni
:
7 9
;
2 11
7 9
+ =
2 11
7 .....
=
2 ......
9 .....
=
11 ......
7 9 ...... ..... ..... + ..... ......
+ =
+
=
=
2 11 ..... ......
.....
......
Esercizi dal libro pag. 375 n° 48 e 49, dal n° 56 al n° 61
Esercizi a pag. 377 dal n° 87 al n° 98
35
4) Calcola
•
3+
9
=
11
9
al minimo comune denominatore
11
3
RICORDA: 3 =
1
9
q Trova il m.c.m. tra i denominatori 3 e
11
Prima riduci
3;
m. c. m. (…..;…..) = …..
3;
Trasforma
q
x ……
3=
9
in frazioni con denominatore uguale al m. c. m. ……
11
x ……
.....
......
9 .....
=
11 ......
:
•
Poi somma
3+
3;
:
9
11
9
=
11
3=
.....
......
9 .....
=
11 ......
9 ...... ..... ..... + ..... ......
3+ =
+
=
=
11 ..... ......
.....
......
15
5) Calcola 15 −
=
4
15
• Prima riduci 15;
al minimo comune denominatore
4
15
RICORDA: 15 =
1
q
Trova il m.c.m. tra i denominatori ….. e ……
m. c. m. (…..;…..) = …..
q
Trasforma
15;
x ……
15 =
:
15
4
.....
......
in frazioni con denominatore uguale al m. c. m. ……
x ……
15 .....
=
4 ......
:
36
•
Poi sottrai
15 −
15;
15
4
15
=
4
.....
......
15 .....
=
4 ......
15 =
15 +
15 ...... ..... ..... + ..... ......
=
+
=
=
4 ..... ......
.....
......
6) Calcola
•
8−
1 3
+ =
2 5
1 3
8; ; al minimo comune denominatore
2 5
.....
RICORDA: 8 =
.....
Prima riduci
q
Trova il m.c.m. tra i denominatori ….. e ……e …..
m. c. m. (…..;…..; …..) = …..
q
Trasforma
1 3
8; ; in frazioni con denominatore uguale al m. c. m. ……
2 5
x ……
8=
.....
......
:
•
Poi sottrai
8−
x ……
x …….
1 .....
=
2 ......
3 .....
=
5 ......
:
1 3
8; ;
2 5
1 3
+ =
2 5
.....
......
1 .....
=
2 ......
3 .....
=
5 ......
1 3 ...... ..... ..... ..... − ...... + ..... ......
8− + =
−
+
=
=
2 5 ..... ..... ......
.....
......
8=
Esercizio:calcola:
3
+4 =
2
3 1 6
+ + +2=
2 2 7
5+
1
=
2
Esercizi dal libro da pag. 375 a pag. 377
37
:
Per moltiplicare due frazioni bisogna moltiplicare tra loro i numeratori e i denominatori
1) Moltiplica
•
2 7
×
3 11
Moltiplica i numeratori tra loro e i denominatori tra loro
2 7 2 × 7 14
× =
=
3 11 3 × 11 33
2) Moltiplica
•
2 5
×
3 9
Moltiplica i numeratori tra loro e i denominatori tra loro
2 5 2 × 5 .....
× =
=
3 9 3 × 9 .....
3) Moltiplica
•
2 1 6
× ×
3 5 7
Moltiplica i numeratori tra loro e i denominatori tra loro
2 1 6 2 × ..... × ..... .....
× × =
=
3 5 7 3 × ..... × ..... .....
4) Moltiplica
•
4 7
×
3 11
Moltiplica i numeratori tra loro e i denominatori tra loro
4 7 .... × ..... .....
× =
=
3 11 ..... × ..... .....
5) Moltiplica
•
3×
3×
9
2
Moltiplica i numeratori tra loro e i denominatori tra loro
9 .... × ..... .....
=
=
2 ..... × ..... .....
38
Prima di moltiplicare riduci le frazioni!
6) Moltiplica
•
7 15
×
10 19
Riduci la frazione.
10 e 15 si possono dividere per 5.
10: 5 = 2, cancello 10 e scrivo 2
15: 5 = 3, cancello 15 e scrivo 3
3
7 15
×
10 19
•
2
Moltiplica i numeratori tra loro e i denominatori tra loro
3
2
7 15 7 × 3 21
× =
=
10 19 2 × 19 38
7) Moltiplica
•
Riduci la frazione.
3 e 9 si possono dividere per 3.
3: 3 = 1, cancello 3 e scrivo 1
9: 3 = 3, cancello 9 e scrivo 3
1
3
•
7 3
×
9 35
7 3
×
9 35
Riduci la frazione.
7 e 35 si possono dividere per 7.
7: 7 = ….., cancello ….. e scrivo …..
35: 7 = ……, cancello ….. e scrivo ….
1
7 1
×
3 35
•
5
Moltiplica i numeratori tra loro e i denominatori tra loro
1 1 1 × 1 .....
× =
=
3 5 3 × 5 .....
39
8) Moltiplica
•
Riduci la frazione.
14 e 28 si possono dividere per …...
…..: ….. = ….., cancello ….. e scrivo …..
…..: ….. = ….., cancello ….. e scrivo …..
……
…..
•
14 25
×
10 28
..... .....
×
..... ......
Riduci la frazione.
14 e 28 si possono dividere per …...
…..: ….. = ….., cancello ….. e scrivo …..
…..: ….. = ….., cancello ….. e scrivo …
……
..... ......
×
...... ......
……
•
Moltiplica i numeratori tra loro e i denominatori tra loro
..... ..... ..... × .... .....
×
=
=
...... ..... ..... × ..... .....
Esercizio
a.
b.
c.
d.
e.
4 12
× =
3 5
44 9
× =
18 11
35 7
× =
49 5
15 24
×
=
3 60
2 8
× =
64 6
Esercizi dal libro pag....... n° .........
40
Per dividere due frazioni:
A) Cambia il numeratore con il denominatore nella seconda frazione
2
7
:
3
11
2 11
×
3 7
=
B) Poi moltiplica i numeratori tra loro e i denominatori tra loro
2 11 2 × 11 22
× =
=
3 7
3 × 7 21
DIVISIONE:
1) Dividi
•
2 7 2 11 2 × 11 22
: = × =
=
3 11 3 7
3 × 7 21
1 3
:
5 7
Cambia il numeratore con il denominatore
1 3 1 7
: = ×
5 7 5 .....
•
Poi moltiplica i numeratori tra loro e i denominatori tra loro
1 3 1 7 ..... × .... ....
: = × =
=
5 7 5 3 .... × .... ....
2) Dividi
•
•
10 8
:
5 13
Cambia il numeratore con il denominatore
Poi moltiplica i numeratori tra loro e i denominatori tra loro
10 8 .... ..... ..... × .... ....
: = ×
=
=
5 13 5 ..... .... × .... ....
Esercizio
3 4
a.
: =
16 5
17
b.
: 5=
12
41










