dispense - e

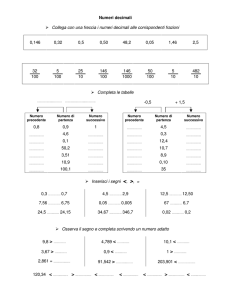
Numeri - teoria - 9
l'insieme Q dei numeri razionali relativi
La successiva estensione all'insieme Q dei numeri razionali è motivata
da esigenze analoghe a quelle viste a proposito dell'insieme Z:
rendere sempre possibile l'operazione di divisione (con l'eccezione del
divisore nullo); in altre parole si tratta di trovare un ambiente nel quale tutte le
equazioni del tipo x.b = a (con b≠0) ammettano soluzione (si noti che in Q si
trova il quoziente non solo fra due numeri interi ma anche fra due numeri
razionali, purché il divisore sia diverso da 0);
per la misura delle grandezze l'insieme Z in molti casi non è adeguato;
estendere il legame fra insieme dei numeri e insieme dei punti di una retta:
come fra due punti distinti di una retta ce n'è sempre un altro, così è
ragionevole cercare un insieme di numeri in cui valga una proprietà analoga.
Ricordiamo in proposito che un insieme ordinato si dice denso se fra due
elementi distinti ne è sempre compreso un altro.
Qualche parola sulla storia. Troviamo esplicitamente frazioni in antichi
documenti che risalgono agli Assiri, ai Babilonesi e agli Egiziani (per questi
ultimi va citato il Papiro Rhind, databile intorno al 1800 a.C., in cui sono in
particolare studiate le cosiddette unità frazionarie, cioè le frazioni con
numeratore 1). Per gli antichi Greci, il nome "numero" spetta solo ai naturali,
ma si parla tranquillamente di rapporti fra numeri.
Per introdurre i numeri razionali, disponiamo di vari metodi intuitivi, come le
tradizionali "torte". Può essere utile anche pensare a operatori su grandezze: in
sostanza, moltiplicando una frazione per un segmento troviamo un altro
segmento: quindi una frazione "opera" su segmenti.
Non si confonda frazione con numero razionale: per esempio, 9/6 e 6/4 non
sono la stessa frazione (hanno numeratori e denominatori diversi), ma
rappresentano lo stesso numero razionale (lo stesso elemento di Q).
Da un punto di vista etimologico, frazione deriva dal latino fractus
(spezzato). Le parole frazione e razionale hanno origini simili: l'aggettivo
razionale non significa qui "ragionevole", ma è legato al latino ratio, nel senso
di rapporto.
Nella terminologia classica, si parla di frazioni proprie (minori di 1),
improprie (maggiori di 1), apparenti (equivalenti ad un intero); si tratta, per la
verità, di una distinzione non necessaria.
Numeri - teoria - 10
Ricordiamo le definizioni di addizione e moltiplicazione nell'insieme Q.
Addizione. La somma (o la differenza) di due frazioni con lo stesso
denominatore è la frazione che ha lo stesso denominatore e ha per numeratore
la somma (o la differenza) dei numeratori:
a b ab
 
.
n n
n
Se le due frazioni da sommare hanno denominatori diversi, ci si riconduce al
caso precedente considerando due frazioni, equivalenti alle date, che hanno per
denominatore il mcm dei denominatori delle frazioni iniziali.
Moltiplicazione. Il prodotto di due frazioni si ottiene moltiplicando i
numeratori e moltiplicando i denominatori:
a c ac
 
.
b d bd
Analogamente, per la divisione, abbiamo
a c a d ad
:   
b d b c bc
L'inversa di una frazione a/b è la frazione b/a. Dividere per una frazione
equivale a moltiplicare per l'inversa.
Esercizi. 1) Eseguire vari esempi di addizioni e moltiplicazioni in Q.
2) Verificare che in Q l'ordine è denso. (Suggerimento: fra i numeri r ed s è
compreso il numero .../2)
3) È vero in Q che se a < b allora ac < bc ? (la risposta è sì, purché c sia
...).
4) Verificare che la definizione di somma a/b + c/d = (a+c) / (b+d) non è
accettabile perché è ambigua, nel senso che considerare due frazioni che
rappresentano lo stesso numero razionale porta a risultati diversi. Infatti, si ha
per esempio 1/2 = 3/6; ma con la definizione precedente 1/2 + 1/3 = 2/5, mentre
3/6 + 1/3 = 4/9 e i due risultati non sono equivalenti fra loro. Inoltre, con la
stessa definizione, si otterrebbe 1/3 + 1/3 = 2/6 = 1/3, che non corrisponde alla
nostra idea di somma.
Molta importanza rivestono le notazioni per numeri razionali. Oltre alle
frazioni, si usano anche numeri decimali limitati o illimitati periodici.
Ricordiamo in proposito le seguenti proprietà.
Eseguendo la divisione a/b (con a, b interi e b > 0), non si può ottenere un
numero decimale illimitato non periodico: i successivi resti sono numeri
naturali minori del divisore b; quindi, prima o poi o, si ottiene come resto 0 e il
Numeri - teoria - 11
risultato è un numero decimale limitato, oppure si ritrova un resto che era già
comparso ed in tal caso il risultato è un numero decimale illimitato periodico.
Supponendo a e b primi fra loro, a/b corrisponde ad un numero decimale
limitato (cioè con un numero finito di cifre dopo la virgola) se e solo se b non
contiene fattori primi diversi da 2 e 5 (si noti che 2 e 5 sono i fattori primi di
10, base del sistema di numerazione).
Ogni numero decimale limitato si può comunque scrivere in forma
periodica: in base 10 abbiamo ad esempio 4,26 = 4,26(0) = 4,25(9) , dove la
parentesi indica il periodo.
*[La regola della "frazione generatrice" consente di risalire da un numero
periodico alla corrispondente frazione. Si osservi il seguente esempio:
x = 4,3(56)
100 x = 435,6(56)
100 x − x = 435,6(56) − 4,3(56) = 435,6 − 4,3
cioè:
99 x = 435,6 − 4,3 e x = (435,6 − 4,3) / 99 = (4356 − 43) / 990. ]*
un'altra proprietà delle operazioni
La sottrazione e la divisione godono (in N, in Z, in Q) della seguente proprietà,
spesso utile nell'esecuzione di calcoli.
Proprietà invariantiva a) Il risultato di una sottrazione non cambia se si
aggiunge o si toglie uno stesso numero ad entrambi i termini della sottrazione:
a ‒ b = (a + n) ‒ (b + n) = (a ‒ n) ‒ (b ‒ n).
Per esempio la differenza di età fra due persone rimane costante nel tempo.
b) Il risultato di una divisione non cambia se entrambi i termini della divisione
sono moltiplicati o divisi per uno stesso numero:
a : b = (a  n) : (b  n) = (a : n) : (b : n).
Si noti, in particolare, che quando semplifichiamo una frazione (passando per
esempio da 18/12 a 3/2) applichiamo proprio la proprietà invariantiva.
Un sottoinsieme di Q è l'insieme D dei numeri decimali limitati, che, nel corso
dell'educazione matematica, costituisce la prima estensione di N.
Se la scrittura posizionale dei numeri naturali è stata correttamente capita
(una decina è uguale a 10 unità, un centinaio è uguale a 10 decine, ecc.),
l'estensione all'insieme D dei numeri decimali dovrebbe risultare abbastanza
spontanea: un'unità è uguale a 10 decimi, un decimo è uguale a 10 centesimi,
ecc.
Gli elementi di D corrispondono alle frazioni decimali, cioè che hanno per
denominatore una potenza di 10. Per esempio
7/4 = (725) / (425) = 175/100 = 175/102 = 1,75.
Numeri - teoria - 12
Gli algoritmi per eseguire le operazioni in D sono sostanzialmente gli
stessi usati per i numeri naturali. Naturalmente va posta attenzione alla
posizione della virgola nel risultato, specialmente nel caso del prodotto di due
numeri e nel caso del resto di una divisione.
Esercizi. a) Sapendo che 12×23 = 276, calcolare:
1,2×2,3,
0,12×23,
0,12×0,23,
1200×0,023
b) Per calcolare il quoziente intero della divisione 15 : 1,2 conviene
moltiplicare dividendo e divisore per 10 (cioè calcolare 150 : 12) Quali sono
quoziente intero e resto della divisione 15 : 1,2 ? [il resto è 0,6]
Confrontiamo D con i precedenti insiemi numerici, tenendo presente che
ogni decimale limitato è razionale: si ha N  D  Q (il simbolo "" significa
sottoinsieme, ovvero contenuto in); accettando i numeri decimali negativi, si ha
anche Z  D. Considerando l'insieme D al posto di Q si ottengono alcuni
vantaggi: in particolare, le regole di calcolo sono più semplici, perché vengono
ricondotte a quelle fra numeri interi. L'insieme D è adeguato per gli scopi
pratici ed è denso: fra due numeri decimali limitati ne è sempre compreso un
altro (quali numeri decimali compresi fra 3 e 3,1?). Tuttavia, D non contiene
l'inverso di ogni suo elemento (per esempio l'inverso di 3 è 1/3, che non
appartiene a D); inoltre, il fatto che un razionale sia o no un elemento di D
dipende dalla base del sistema di numerazione usato (nel nostro caso 10), per
cui l'insieme D cambia al cambiare della base.
Con l'introduzione dell'euro, i numeri decimali sono entrati nella pratica
quotidiana di tutti, sia pure con la limitazione di due sole cifre dopo la virgola.
Per altro, il linguaggio dell'euro è in parte diverso la linguaggio matematico:
per esempio, non si dice usualmente "mezzo euro" per indicare 50 centesimi
(negli USA c'è una moneta che vale half dollar, ma non è molto diffusa) e
nessuno dice "un decimo di euro" per indicare 10 centesimi. Inoltre, anche se la
cifra dei centesimi è 0, si preferisce sempre scriverla: non si usa, cioè, una
scrittura come € 7,2.
Infine, si tenga presente che l'uso della "virgola" e del "punto" in molti
paesi stranieri (in particolare nei paesi di lingua inglese) è diverso da quello
italiano: ad esempio, la scrittura 35,605.4 indica il numero che noi denotiamo
con 35 605,4.
Numeri - teoria - 13
Il passaggio dai numeri razionali all'insieme R dei numeri reali è
suggerito da varie esigenze. Dal punto di vista algebrico si tratta di trovare un
sistema numerico in cui esistano le radici di tutti i numeri positivi. In
geometria, l'esistenza di grandezze incommensurabili mostra che i numeri
razionali non sono sufficienti per misurare tutti i segmenti. Proprio la
riflessione sull'usuale procedimento di misura in cui, ricorrendo via via ai
successivi sottomultipli decimali dell'unità di misura, si ottiene un allineamento
decimale (non necessariamente né limitato né periodico) sembra una strada
convincente per motivare l'introduzione di R.
Con l'introduzione dei numeri reali si ottiene una corrispondenza
biunivoca fra l'insieme dei numeri e l'insieme dei punti di una retta: a ogni
numero corrisponde un punto e viceversa.
Storicamente, la necessità di considerare anche numeri non razionali per la
misura di segmenti risale ai Pitagorici: la leggenda vuole che Ippaso da
Metaponto (V sec. a.C.) sia stato punito per aver divulgato la scoperta di
segmenti incommensurabili.
Il principio di induzione in N
Principio di induzione in N. Sia F(n) una proprietà o una formula (che dipende
da un numero n) tale che:
a) F(0), cioè F vale per il numero 0;
b) nN [F(n)  F(n+1)], cioè se F vale per un numero, vale anche per il
successivo. [la freccia "" significa implica, ovvero se ... allora ...]
Allora n F(n), cioè F vale per tutti i numeri.
Il principio di induzione può essere formulato anche nel seguente modo. Sia A
un sottoinsieme di N tale che:
a) 0A;
b) n [nA  (n+1)A].
Allora A = N.
Esempio. Dimostriamo per induzione che per ogni numero naturale n si ha:
0+1+…+n=
nn  1
2
La proprietà F(n) è appunto l'uguaglianza 0 + 1 + … + n =
nn  1
.
2
Numeri - teoria - 14
La proprietà vale per 0, perché 0 = 0·1/2. Può essere utile, anche se a rigore
non è necessario, controllare che la proprietà vale anche per 1, per 2, per 3.
Supponiamo che la proprietà valga per un numero n, cioè supponiamo che
nn  1
e dimostriamo che la stessa formula vale anche se al
2
n  1n  2
posto di n scriviamo n+1, cioè 0 + 1 + … + n + n+1 =
.
2
0+1+…+n=
In effetti, 0 + 1 + … + n + n+1 = (0 + 1 + … + n) + n+1 che, per l'ipotesi
induttiva, è uguale a
n  1n  2
nn  1
+ n+1 = ... =
.
2
2
Questo conclude la dimostrazione: la formula vista vale per tutti i numeri
naturali n.
Si ottiene una giustificazione di carattere intuitivo del principio di
induzione osservando che la proprietà F(n) vale per 0 (per ipotesi); quindi vale
per il successore di 0, cioè 1; quindi per il successore di 1, cioè 2; ecc. Proprio
in riferimento ad un ragionamento del tipo descritto, il grande matematico
Henri Poincaré diceva che "il principio di induzione riassume in un'unica regola
infiniti sillogismi".
Una dimostrazione del principio di induzione è la seguente.
*[Nelle ipotesi citate, sia per assurdo n0 il minimo numero per cui non vale
F(n). Ora, n0 è diverso da 0 per la condizione a); dunque ha senso considerare il
numero n0−1, e per questo numero vale F(n0) (perché n0 è il minimo per cui non
vale). Risulta allora F(n0−1), ma non F(n0), in contrasto con la condizione b). In
conclusione non può esistere alcun numero per cui non vale F(n).]*
La dimostrazione appena esposta è corretta; ma, a rigore, abbiamo usato il
principio del minimo numero, che si enuncia dicendo che "ogni sottoinsieme
non vuoto di N ammette minimo" e che equivale al principio di induzione.
Ci sono varie metafore convincenti. Pensiamo a un treno, con infiniti vagoni,
ciascuno collegato al successivo (in modo che se un vagone si muove si muova
anche il successivo). Se il primo vagone si muove, allora si muove tutto il treno.
Oppure pensiamo a carte disposte "in piedi" su un tavolo in modo tale che se
una cade cada anche la successiva; se facciamo cadere la prima carta, ...
In alcuni casi non è possibile assumere come base induttiva il caso n=0.
Ad esempio, l'affermazione "la somma delle ampiezze degli angoli interni di un
poligono con n lati è (n−2).180°" è sensata per n ≥ 3; per cui la dimostrazione si
effettua a partire da n = 3. In questi casi il principio di induzione si enuncia
così: sia A  N; supponiamo che, per un opportuno numero m0, sia m0A e
Numeri - teoria - 15
inoltre, per n≥m0, valga l'implicazione "se nA allora (n+1)A"; allora A
contiene tutti i numeri maggiori o uguali ad m0.
Esercizi. Dimostrare per induzione le seguenti uguaglianze:
2
n
n+1
1+2+2 +…+2 = 2 ‒1
(0 + 1 + 2 + … + n)2 = 03 + 13 + … + n3
0.1 + 1.2 + 2.3 + … + n(n+1) = Error!
Esercizio. Dimostrare che la somma dei primi n numeri dispari è uguale ad n2.
definizione induttiva delle operazioni
(addizione)
Premettiamo che la scrittura y+ indica "il successivo di y", cioè y+1.
La definizione è data per induzione sul secondo termine: per ogni x, prima si
definisce il valore di x + 0; dopo di che, supponendo noto il valore x + y, si
definisce x + y+.
x (x + 0 = x);
xy [x + y+ = (x + y)+].
(moltiplicazione) x (x.0 = 0);
xy (x.y+ = x.y + x).
Vediamo con un esempio che la definizione porta ai consueti risultati:
4.2 = 4.1+ = 4.1 + 4 = 4.0+ + 4 = 4.0 + 4 + 4 = 0 + 4+ 4 = 4 + 4.
(elevamento a potenza) x (x0 = 1)
purché x  0;
(y+)
y
xy (x = x x).
un esempio di applicazione del calcolo alle differenze finite
Consideriamo n rette nel piano. Ci proponiamo di stabilire in quante parti al
massimo le rette scompongono il piano.
Se n = 0, abbiamo 1 sola parte, cioè il piano stesso.
Se n = 1, abbiamo una retta che divide il piano in 2 parti.
Se n = 2, abbiamo al massimo 4 parti di piano.
Se n = 3, abbiamo al massimo 7 parti di piano.
Se n = 4, abbiamo al massimo 11 parti di piano.
Numeri - teoria - 16
Per trovare una formula generale è utile il calcolo alle differenze finite.
Vediamo in che cosa consiste. Scriviamo la successione ottenuta e la
successione delle differenze fra numeri consecutivi, cioè:
1
2
4
7
11 …
1
2
3
4
…
Iterando il calcolo delle differenze si ottiene:
1
1
1 …
A questo punto ci fermiamo, perché la differenza fra ogni numero e il
precedente è costante. Assumendo che ciò sia vero anche per i numeri
successivi, applichiamo il seguente
Teorema. Se con n passaggi (differenze) si ottiene una successione costante,
allora la successione originaria si può esprimere con un polinomio di grado n.
Nel nostro caso abbiamo dunque a che fare con un polinomio di secondo
grado, ovvero del tipo an2 + bn + c. Determiniamo a, b, c mediante i valori già
noti.
Per n = 0, si ottiene an2 + bn + c = 1, dunque c = 1.
Per n = 1, si ottiene an2 + bn + c = 2, dunque a + b + c = 2.
Per n = 2, si ottiene an2 + bn + c = 4, dunque 4a + 2b + c = 4.
La soluzione del sistema è: c = 1, a = b = 1/2.
In conclusione, il polinomio è (n2 + n)/2 +1. Per ogni n il polinomio fornisce il
numero massimo di parti in cui le n rette scompongono il piano; per esempio,
10 rette scompongono il piano al massimo in 56 parti.