Un teorema sul gioco del lotto
In una raccolta d’opuscoli e scientifici e filologici, edita a Venezia nel
1735, il matematico Giulio Carlo de’ Fagnani presenta una formula
per stabilire il giusto premio spettante ad un giocatore del lotto in
base alla combinazione giocata ed alla somma spesa. Ecco il testo
originale:
Chiamisi (u) la moltitudine de’ numeri che stanno nell’urna, (e) la
moltitudine de’ numeri, che se n’estraggono, (g) la moltitudine de’
numeri, che si giocano combinati insieme; v. g. se si gioca un numero
solo, o un ambo, o un terno ec. g rappresenta rispettivamente un
numero solo, o un ambo, o un terno ec.
Chiamisi in oltre (f) la moltitudine di quei numeri della combinazione
(g), che debbono avere un luogo, o sia ordine fisso nell’estrazione; v. g.
se si gioca un numero solo con questa condizione, che il numero giocato
sia il primo estratto, allora f significherà l’unità; se si gioca un ambo
con la condizione, che due, ovvero uno de’ numeri dell’ambo abbiano un
luogo fisso nell’estrazione, allora f denoterà 2, ovvero rispettivamente 1
(..).
Finalmente, se nel numero giocato non vi è la condizione, che alcuno
de’ numeri abbia un luogo fisso nell’estrazione, in questo caso f
significherà zero.
Teorema generale
Poste le suddette significazioni, e definizioni, e posto ancora, che (d)
rappresenti la spesa contribuita dal giocatore, e (p) la ricompensa, che
se gli debbe, allorché vince; io dico, che sussiste l’equazione seguente:
p = (u+1,...., u-g)d/(e-f+1,...., e-g) - d.
Nella notazione di Fagnani, la scrittura (m,...,n), ove m,n sono numeri
naturali (il primo maggiore del secondo) indica il prodotto di tutti i
numeri strettamente compresi fra n e m. Se m=n+1, quella scrittura
indica il numero 1.
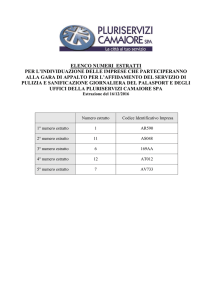
In base al Teorema Generale di Fagnani, è possibile, ad esempio,
calcolare il premio spettante ad un giocatore che realizzi un 5+1 al
Superenalotto con una schedina da 1900 lire. Il giocatore gioca una
combinazione vincente puntando su questa 950 lire. I numeri
nell’urna sono u=90, i numeri estratti sono e=7, i numeri giocati g=6.
Il giocatore indovina il settimo estratto (il numero jolly), e cinque dei
precedenti estratti. Poiché egli non precisa quale dei numeri da lui
giocati debba essere il settimo estratto, è come se giocasse 6 volte la
stessa combinazione, in cui il settimo estratto occupa sei diverse
posizioni. Per ciascuna di queste f=1. Dunque egli vince con una
combinazione su cui ha puntato 950/6 lire. Il Teorema Generale
stabilisce che la giusta ricompensa è:
p = (91,…,84)950/6(7,…,1) = 85·86·87·88·89·90 ·950/2·3·4·5·6·6 -950
= 98.580.648.800,
più di 98 miliardi!