14
Ottica
In questo capitolo si introduce l’ottica non tanto come
risultato della sistemazione dell’elettromagnetismo operata da Maxwell, quanto come frutto di un cammino indipendente della scienza lungo il quale progressi teorici
e sviluppi di enorme importanza pratica sono andati di
pari passo. Inizieremo presentando i fenomeni che hanno
aiutato a comprendere la natura fisica della luce: riflessione, rifrazione, dispersione, interferenza, diffusione e
polarizzazione. Il modello ondulatorio della luce è stato
lo strumento che ha consentito di inquadrare buona parte di questa fenomenologia portando, molto prima di
Maxwell, a dispositivi che si sono rivelati fondamentali
nello studio della natura: microscopi, telescopi, spettrometri. Daremo qui solo scarni cenni allo sviluppo
dell’ottica fisica, ma ricordiamo che il vastissimo tema
dell’interazione tra luce (od onde elettromagnetiche) e
materia, ripreso nel prossimo capitolo, è ben lungi
dall’essere concluso, o dall’aver esaurito il suo potenziale di sviluppo tecnologico.
Per quanto riguarda l’ottica geometrica si presenta
l’applicazione delle leggi della riflessione e rifrazione
allo studio delle proprietà di semplici strumenti ottici. I
casi facilmente trattabili sono praticamente solo quelli
che prevedono superfici riflettenti o rifrangenti di tipo
sferico. Nei limiti di alcune ragionevoli approssimazioni,
valgono equazioni semplicissime che descrivono però situazioni diverse, che possono essere distinte padroneggiando una “regola dei segni”.
14.1 Riflessione e rifrazione
I fenomeni luminosi hanno da sempre affascinato filosofi,
naturalisti e poeti: Dante riempie la sua Commedia di
immagini e visioni e rappresenta Dio come una sorgente
di luce. Specchi e lenti primitive erano utilizzati fin
dall’antichità; ma è nel Rinascimento che prende inizio
quello sviluppo tecnologico che porterà, nel Seicento,
all’invenzione di microscopio e telescopio. Nello stesso
periodo si avviò un dibattito sulla natura della luce che si
risolse con il trionfo della teoria ondulatoria dell’olandese Christian Huygens.
La teoria alternativa a quella di Huygens era la teoria
corpuscolare di Cartesio e Newton: può essere istruttivo
metterle a confronto per avere una idea di quale fossero i
termini del dibattito e lo stato delle conoscenze. Lo scopo
principale delle due teorie era quello di interpretare i fenomeni della riflessione e della rifrazione. Un raggio di
luce(☯) che incide su uno specchio produce un raggio riflesso che forma con la normale allo specchio un angolo
di riflessione uguale a quello di incidenza. Se il raggio
raggiunge la superficie di separazione di due mezzi trasparenti, si può osservare un raggio rifratto che si propaga nel secondo mezzo formando con la normale alla superficie un angolo di rifrazione diverso da quello di incidenza. Il rapporto tra seno dell’angolo di incidenza e seno dell’angolo di riflessione è costante e dipende dalla
natura dei due mezzi trasparenti. Raggio riflesso e raggio
rifratto appartengono al piano individuato da raggio incidente e normale alla superficie (piano di incidenza).
Riprendendo l’opera di Cartesio (in particolare, La
diottrica, nel Discorso sul Metodo del 1637) Newton argomentò (1696) che un raggio di luce fosse costituito da
uno sciame di particelle “luminifere”, elastiche, con dimensioni e masse infinitesime, espulse a grandissima velocità dalla sorgente luminosa e sottoposte alle leggi della
(☯) Per raggio di luce si intende la linea uscente dalla sorgente luminosa tracciata lungo il percorso della luce. In un
mezzo omogeneo e isotropo (con uguali proprietà in ogni direzione) il raggio luminoso è una semiretta.
302 Capitolo 14
meccanica. La riflessione è facilmente spiegata supponendo che il raggio riflesso contenga i corpuscoli che sono rimbalzati sulla superficie. Infatti, durante un urto elastico contro una superficie, la componente tangenziale alla superficie della velocità della particella rimane inalterata mentre la componente normale cambia di segno.
Sembra poi ragionevole attendersi che il corpuscolo che
attraverserà la superficie di separazione sia sottoposto a
forze normali alla superficie, che ne cambieranno quindi
la componente normale della velocità, ma non quella tangenziale.
I fenomeni della riflessione e rifrazione sono schematizzati nella figura seguente che illustra anche la teoria di
Newton. Le frecce piene indicano le direzioni di propagazione dei tre raggi nel piano di incidenza. Il raggio incidente proviene dal mezzo 1 (bianco) e forma l’angolo α
con la normale alla superficie; quello riflesso forma un
angolo α' = α mentre quello rifratto forma un angolo
α"< α (come atteso quando il secondo mezzo, quello
grigio, è più denso di quello bianco).
velocità è tanto maggiore quanto maggiore è la densità
del mezzo. Solo nell’Ottocento si provò che tale predizione è in contrasto con l’esperienza; al tempo di Newton
la velocità della luce non era ancora stata determinata.
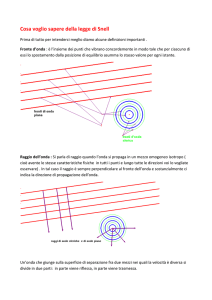
Il Traité de la Lumière di Huygens venne pubblicato
nel 1690. Vi si affermava che la luce è una perturbazione
che si propaga nello spazio circostante le sorgenti luminose mediante un meccanismo simile a quello di propagazione delle onde in un mezzo elastico. Un fronte
d’onda è una superficie dove, a un dato istante, lo spostamento dovuto all’onda è massimo; la direzione del
raggio luminoso va identificata con la normale al fronte
d’onda. Ogni punto di un fronte d’onda può essere considerato come una sorgente luminosa, origine di raggi secondari in tutte le direzioni, la sovrapposizione dei quali
produce i fronti d’onda successivi. Supponiamo che la
luce arrivi dal mezzo 1 dove la sua velocità di propagazione v1 è minore di quella nel secondo mezzo v2. Nella
figura le frecce indicano i raggi e le linee tratteggiate i
fronti d’onda.
v||
v⊥
α α'
v'⊥
A'
v||
1
B
α α'
2
1
α"
2
v"⊥
B'
A
α''
A''
Secondo Newton, la componente tangenziale della velocità del corpuscolo incidente, v|| , è comune anche a raggio rifratto e riflesso; la componente normale della velocità del raggio riflesso viene cambiata di segno, v'⊥ = −v⊥
mentre, per il raggio rifratto della figura, la componente
normale v"⊥ è maggiore di v⊥. I raggi sono stati rappresentati da segmenti con lunghezze proporzionali alle velocità delle particelle luminifere. Il raggio incidente e
quello riflesso hanno velocità v1, quello rifratto velocità
v2. Dalla figura si ricava la legge della rifrazione
v || = v1 sin a = v 2 sin a" ⇒
sin α
=
sin α "
v2
v1
14.1
La conclusione da trarre è che i corpuscoli luminiferi
hanno velocità caratteristica in ogni mezzo e che la loro
Si è rappresentato con la linea AB il fronte d’onda incidente a un certo istante iniziale. Dopo un tempo T, il punto B si è trasferito in B', con |BB'| = v1T, mentre l’onda
secondaria emessa da A è distribuita su una semisfera di
raggio v1T nel mezzo 1 e su una semisfera di raggio v2T
nel secondo mezzo. Gli inviluppi delle onde secondarie
sono B'A' nel mezzo 1 e B'A" nel mezzo 2; questi segmenti rappresentano i fronti dell’onda riflessa e di quella
rifratta al tempo T. Dall’uguaglianza dei triangoli rettangoli AB'A' e AB'B si ha
sin α =
|BB'| |AA'|
=
= sin α '
|AB'| |AB'|
da cui si ricava α = α ' , ovvero la legge della riflessione:
l’angolo di incidenza è uguale all’angolo di riflessione.
Ottica 303
Per ipotesi si ha inoltre
|AA'| = v1T
n1 ≡
|AA"| = v2T
14.3
pari al rapporto tra la velocità della luce nel vuoto e la
velocità nel mezzo 1 è detta indice di rifrazione assoluto del mezzo 1. Con questa definizione la 14.2 si riscrive
e dai triangoli rettangoli ABB" e AA"B' si ricava
| AB' | =
c
≈ ε r1
v1
v1T
v T
= 2 ⇒
sin α sin α "
ε r2
sin α n 2
=
=
= n2,1
sin α " n1
ε r1
sin α
v
= 1
sin α " v 2
14.2
che è la legge della rifrazione, o legge di Snell: il rapporto tra seno dell’angolo di incidenza e seno di quello
di riflessione è una costante, specifica dei due mezzi, pari
al rapporto delle velocità della luce nei due mezzi.
Si noti che Newton prevedeva (14.1) un rapporto di
velocità che è il reciproco di quello dato dalla 14.2.
Sempre nel Seicento, il matematico Pierre de Fermat
ricondusse le leggi di riflessione e rifrazione a un principio unico ed elegante: un raggio luminoso che passa tra
due punti segue, tra tutti i cammini possibili, quello che
richiede il tempo di percorrenza minimo o massimo
(principio di Fermat). Anziché di tempo di percorrenza
è comodo parlare di cammino ottico, definito come la
distanza che la luce coprirebbe nel vuoto nel tempo richiesto dal tragitto. Secondo il principio di Fermat, la luce segue sempre il percorso con il minimo cammino ottico; si propaga perciò lungo una retta in un mezzo dove la
velocità della luce sia costante.
14.4
dove n2,1 è l’indice di rifrazione relativo del mezzo 2
rispetto al mezzo 1. Quando il mezzo 1 è l’aria (n1 ≈ 1),
gli indici di rifrazione assoluti e relativi in pratica coincidono. Un materiale è tanto più rifrangente tanto più elevato è il suo indice di rifrazione.
Quando la luce passa da un mezzo più rifrangente
come l’acqua (nacqua ≈ 4/3 ≈ 1.33) a uno meno rifrangente, come l’aria (naria ≈ 1.00), dalla 14.4 si ha
sin α =
naria
1.00
sin α " =
sin α "
nacqua
1.33
Per un certo angolo di incidenza detto angolo limite αc
(≈ 48°35' nel caso acqua-aria) si ha α" = 90° e il raggio
rifratto è radente la superficie di separazione dei due
mezzi. Per angoli di incidenza superiori ad αc il raggio rifratto non esiste perché richiederebbe un angolo di rifrazione con sinα" > 1. Non esistendo l’angolo di rifrazione
che soddisfi la legge di Snell, in questo caso il raggio incidente genera solo il raggio riflesso e si ha la cosiddetta
riflessione totale.
fibra ottica
14.1.1 L’indice di rifrazione
Nel Capitolo 11 si è trovato che la velocità nella luce nel
vuoto è
c=
1
ε 0 µ0
αc
≈ 3(108 ) m/s
In un mezzo di costante dielettrica relativa εr e permeabilità magnetica relativa µr ≈ 1 (come è il caso di quasi tutti
i materiali trasparenti alla luce) la velocità della luce diventa
v=
1
εµ
La quantità
=
1
1
ε 0 µ0
ε r µr
≈
c
εr
Le fibre ottiche sono fili di materiale rifrangente (vetroso o plastico) in aria (o altro materiale meno rifrangente)
che operano in regime di riflessione totale. Per curvature
modeste del tratto di fibra ottica mostrato in figura, la luce che si propaga in direzione prossima all’asse della fibra raggiunge sempre il confine della fibra con angoli di
incidenza superiori ad αc e non esce mai dalla fibra.
304 Capitolo 14
Secondo la 14.3, l’indice di rifrazione assoluto di un
materiale ha un valore che dipende dalla sua costante dielettrica. Nel Capitolo 12 si è accennato al fatto che tale
“costante” in realtà dipende dalla frequenza del campo
elettrico applicato, e quindi dalla lunghezza d’onda della
luce. A parità di angolo di incidenza, onde luminose con
frequenze, o lunghezze d’onda, diverse potranno dare origine a raggi rifratti che si propagano secondo direzioni
distinte. Il fenomeno per il quale un raggio rifratto si separa nelle sue componenti “monocromatiche” (ossia caratterizzate da una sola lunghezza d’onda) a causa del diverso indice di rifrazione che queste presentano è chiamato dispersione della luce.
Il vetro disperde abbastanza bene la luce bianca che
risulta dalla sovrapposizione di onde a differente lunghezza d’onda (e differente “colore”); queste onde si separano passando attraverso un prisma di materiale trasparente e disperdente quale il vetro.
ferenza;
2. diventò l’esperimento destinato a diventare il banco di
prova di ogni teoria ondulatoria; mostreremo infatti
che il modello corpuscolare della luce avrebbe dato
risultati completamente diversi da quelli ottenuti da
Young.
L’esperimento di Young delle due fenditure è rappresentato nella figura seguente.
r1
r2
1
ϑ
d
bianco
λ
violetto
Nella figura si è mostrato sulla destra uno schermo con
fenditura posta in corrispondenza del raggio di luce rossa.
Cambiando la posizione della fenditura si fa passare la
luce a lunghezze d’onda (colori) differenti. Questo è il
principio di funzionamento di un tipo di monocromatore, un dispositivo che seleziona una componente “monocromatica” (idealmente, con una sola lunghezza d’onda)
della luce.
14.2 L’interferenza
La conferma decisiva della correttezza della teoria di Huygens venne quasi un secolo più tardi dall’esperimen-to
di interferenza di Thomas Young (1801), un medico che
contribuì a molti campi della fisica (teoria della elasticità,
della capillarità, della visione) e avanzò per primo
l’ipotesi che la luce fosse un’onda trasversale. Questo esperimento è importantissimo per due ragioni:
1. mise in evidenza in modo esemplare un fenomeno,
quello della interferenza, che svolge un ruolo importantissimo in ottica; si vedrà in seguito che anche la
diffrazione è spiegabile con il meccanismo della inter-
linea dei ventri
2
rosso
dsinϑ
x
i
n
t
e
n
s
i
t
à
L
Un’onda piana monocromatica, con lunghezza d’onda λ
investe normalmente due “strette” fenditure, praticate su
di uno schermo opaco, a una “piccola” distanza d l’una
dall’altra. L’onda piana fu ottenuta da Young facendo arrivare sul foro di un altro schermo, sufficientemente distante dalle due fenditure, la luce uscente da un monocromatore. Questo dettaglio è importante: Young voleva
garantire che la luce giunta alle fenditure provenisse da
un’unica sorgente. Le fenditure stesse sono tanto strette
da potersi considerare puntiformi e, quindi, sorgenti di
onde secondarie sferiche (vedi seguito).
Nel piano del disegno, abbiamo rappresentato due
fronti d’onda successivi delle onde secondarie generate
dalle fenditure 1 e 2. Si nota che questi fronti d’onda si
intersecano nei punti cerchiati, che sono ventri, ossia
punti dove le vibrazioni dovute alle onde 1 e 2, di ampiezza A1 e A2, hanno sempre segno concorde (vedi Capitolo 7). Si dice che nei ventri le vibrazioni delle due onde
secondarie arrivano in fase; qui le ampiezze delle due
onde si sommano dando una vibrazione complessiva con
ampiezza massima A1 + A2.
Consideriamo ora due raggi paralleli r1 e r2, provenienti dalle due fenditure, che si propagano in una dire-
Ottica 305
zione che forma un angolo ϑ con la normale allo schermo. Per giungere sul piano del fronte d’onda indicato con
tratteggio, il raggio r2 deve compiere un tragitto che è più
lungo del tratto dsinϑ rispetto al tragitto del raggio r1. Le
due vibrazioni che si propagano nella direzione individuata da ϑ saranno perciò sfasate di un angolo δϕ dato da
(vedi Capitolo 7)
δϕ ( rad ) = 2π
d sin ϑ
λ
14.5
Imponendo che in questa equazione sia δϕ = 0, 2π,
4π, ... , 2nπ (con n intero), si trovano le direzioni di propagazione, che indicheremo con ϑmax, lungo le quali si
propagano onde con ampiezza massima:
sin ϑ max =
λ
d
n
|n| ≤ d/λ
14.6a
La 14.6a individua le direzioni delle linee dei ventri, le
direzioni privilegiate lungo le quali le due onde sono in
fase e l’intensità dell’onda luminosa (proporzionale al
quadrato dell’ampiezza di vibrazione) è massima. Quando la differenza di cammino è multiplo dispari di
λ/2, δϕ = π, 3π, ... , (2n + 1)π, l’oscillazione di un’onda
secondaria avviene nel verso opposto a quello dell’altra e
si hanno punti, detti nodi, dove l’intensità dell’onda risultante è minima. Dalla 14.5 si ha che le direzioni ϑmin delle linee dei nodi sono
sin ϑ min
1
λ
= n + con |n + 1/2| ≤ d/λ
d
2
14.6b
I raggi luminosi uscenti dalle due fenditure vengono raccolti da un secondo schermo, parallelo al piano delle fenditure, a distanza L >> d. Detta x la distanza dal punto
centrale O dello schermo (vedi figura) si ha, per x << L
sinϑ ≈ ϑ(rad ) ≈
x
L
Introducendo questa relazione nelle 14.6 si hanno le ascisse dei punti dove le ampiezze di vibrazione sono
massime e minime
x max
Lλ
≈
n
d
x min ≈
Lλ
d
n + 1
2
14.7a
14.7b
con n = intero ≥ 0. Queste bande luminose (presso xmax)
alternate a bande scure (presso xmin) vengono chiamate
frange di interferenza. Si dice anche che nelle bande
luminose si ha interferenza costruttiva tra le due onde,
mentre nella bande scure si ha interferenza distruttiva.
Se la luce fosse stata costituita dai corpuscoli luminiferi di Newton il risultato sarebbe stato differente. In un
punto x dello schermo di destra l’intensità luminosa I(x),
ossia l’energia luminosa che raggiunge l’unità di superficie nella unità di tempo, sarebbe stata proporzionale al
numero di particelle provenienti dalla fenditura 1 più
quelle provenienti dalla fenditura 2, ossia sarebbe stata la
somma delle due intensità:
14.8
I ( x ) = I1 ( x ) + I 2 ( x )
Poiché ambedue le intensità I1 e I2 decrescono allontanandosi dalla normale per le corrispondenti fenditure,
sullo schermo di destra per |x| > d/2 avremmo osservato
un’intensità decrescente monotonicamente all’allontanarsi da O. Il punto cruciale è che il modello ondulatorio
prevede che si sommino non le intensità, ma gli “spostamenti”, ossia, nel nostro caso, i campi elettrici e magnetici delle onde elettromagnetiche. Nel punto x dello schermo i campi dovuti alle onde provenienti da 1 e 2 hanno
espressioni del tipo
A1 ( x, t ) = A1 ( x ) cos ωt A2 ( x, t ) = A2 ( x ) cos(ωt − δϕ )
dove δϕ è dato dalla 14.5. Poiché l’intensità di un’onda è
proporzionale alla media nel tempo del quadrato del
campo complessivo, l’intensità luminosa in x si scrive
I ( x ) ∝ ( A1 ( x, t ) + A2 ( x, t ))
2
=
t
A 2 ( x ) A22 ( x )
= 1
+
+ A1 ( x ) A2 ( x ) cos(δϕ )
2
2
14.9
Qui, come nel Capitolo 7, si è tenuto conto del fatto che
la media di cos2ω t vale 1/2 e quella di cosω t sinω t vale
zero. Si vede che l’intensità risultante non è data, come
nella 14.8, dalla somma delle intensità dei singoli raggi:
I1 ( x ) + I 2 ( x ) ∝ A12 ( x ) / 2 + A22 ( x ) / 2
poiché a secondo membro della 14.9 vi è un termine di
interferenza proporzionale al prodotto delle ampiezze
dei due campi: A1(x)A2(x)cosδϕ. Nel caso in cui sia possibile porre A1(x) ≈ A2(x) = A, la 14.9 diventa
306 Capitolo 14
I ( x ) ∝ A 2 (1 + cos δϕ ) = A 2
sin 2 δϕ
2
2 sin (δϕ / 2)
14.10
reticolo di diffrazione. Tale dispositivo trasmette una
luce monocromatica solo lungo le direzioni privilegiate
date dalla 14.6a.
È facile verificare che la 14.9 e la 14.10 hanno valore
massimo quando
δϕ
2
= nπ
con
2
n = intero
3
ossia quando vale la 14.6a. Quando il numeratore a secondo membro della 14.10 si annulla (ossia δϕ = kπ)
mentre il suo denominatore vale 2 (ossia k è dispari,
k = 2n + 1) l’intensità nella 14.10 è nulla, vale la 14.6b e
sullo schermo la frangia è scura.
Se le due fessure nell’esperimento di Young fossero
state illuminate da due sorgenti diverse, la differenza di
fase tra le due onde dopo la fessura avrebbe assunto un
valore δϕ qualunque, mutevole da istante a istante, il valor medio di cosδϕ nella 14.9 sarebbe stato nullo, come
nullo sarebbe stato in media il termine di interferenza. In
tale caso, l’intensità prevista dalla teoria ondulatoria avrebbe coinciso con quella prevista dalla teoria corpuscolare. Per osservare il fenomeno di interferenza è fondamentale che le due sorgenti siano coerenti, ossia che vi
sia una relazione di fase fissa tra l’onda emessa da 1 e
quella emessa da 2. Per questo Young illuminò le due
fenditure con luce proveniente da un’unica sorgente.
Dalle espressioni 14.7 si vede che, noti i parametri
geometrici dell’esperimento di Young, L e d, dalla distanza tra frange luminose successive è possibile ricavare
la lunghezza d’onda della luce. Per apprezzare la cura
che Young dovette impiegare nella realizzazione del suo
esperimento, valutiamo invece a che distanza vanno poste
le fenditure se L = 1 m, la luce monocromatica impiegata
ha lunghezza d’onda λ = 0.5 µm e vogliamo avere una
distanza tra frange luminose successive di 1 mm. Dalla
14.7a otteniamo d = 0.5 mm.
Nella 14.10 la funzione trigonometrica (1 + cosδϕ) è
stata riscritta come quoziente di funzioni trigonometriche.
La ragione è che l’espressione a destra nella 14.10 può
essere generalizzata al caso dell’intensità luminosa IN(ϑ)
che si propaga a un angolo ϑ con la normale a una schiera di N fessure equidistanti e parallele:
sin 2
I N (ϑ ) ∝
sin
1
Nδϕ
2
2 δϕ
con δϕ =
2π d sin ϑ
λ
2
Una schiera di fenditure regolarmente spaziate è detto un
ϑ
(N−1)d sinϑ
N
Confrontando gli andamenti delle intensità prodotte da
due fessure (N = 2, I2(ϑ)) e da otto fessure (N = 8, I8(ϑ))
nel caso in cui d = 2λ si vede che le posizioni di massimi
e minimi coincidono, ma che, al crescere di N, i massimi
di intensità diventano sempre più netti e stretti. Per N
molto grande, praticamente tutta l’energia si propaga solo
nelle direzioni che soddisfano alla 14.6a.
1
I 2 (ϑ )
I 2 (0)
I8 (ϑ )
I 8 (0)
.5
0
-40°
0°
40°
ϑ
Se la schiera di fenditure è investita parallelamente da un
fronte un’onda monocromatico, come indicato nella figura, produce dei raggi nelle direzioni “magiche” che soddisfano la 14.6a. Viceversa, se la schiera riceve un’onda
piana che si propaga secondo uno di questi angoli magici,
emette un’onda piana in direzione perpendicolare al piano delle fenditure. Perciò la schiera di fenditure parallele
agisce, in un certo senso, come un mezzo rifrangente che
cambia la direzione di propagazione dei raggi luminosi.
Si può anche dire che la somma dei segnali rivelati alle
fenditure è massima quando, rispetto al piano delle fenditure, la sorgente (lontana) è vista sotto un angolo zenitale
complementare a quello della 14.6a.
Le serie di bastoncelli paralleli delle comuni antenne
Ottica 307
televisive va considerata come una schiera di fenditure; la
loro orientazione e separazione determina direzioni e
lunghezze d’onda per le quali il segnale captato è massimo. Per rivelare i deboli segnali delle sonde interplanetarie si combinano i segnali di schiere di grandi antenne
paraboliche (di tipo concettualmente simile a quello dei
dischi per la ricezione da satellite), a volte distribuite su
più di un continente.
Una pellicola sottile di spessore d e indice di rifrazione nl
con una faccia in aria (naria ≈ 1) viene investita da
un’onda piana con angolo di incidenza α. Parte dell’onda
incidente è riflessa alla separazione aria/pellicola in A;
parte viene rifratta nella pellicola per poi riflettersi sulla
seconda faccia in B e riemergere dalla prima faccia in C',
parallelamente al raggio riflesso AC.
α
C
A
C'
nl
d
α"
nvetro≈1.5
B
Il fronte d’onda CC' è somma di due raggi: il primo che
ha compiuto il tragitto AC in aria, il secondo che ha
compiuto il tragitto ABC'. La differenza di fase tra i due
tragitti richiede il calcolo del cammino ottico del percorso ABC':
(| AB|+|BC|) nl = 2| AB| nl =
2dnl
cos α "
e del tratto AC
| AC| =|AC' |sin α = 2d tan α " sin α
Usando la legge di Snell 14.4
sin α
= nl
sin α "
2dnl
− 2d tan α "sin α =
cos α "
2d ( nl − sin α " sin α )
=
=
cos α "
δl =
= 2dnl cos α " = 2dnl 1 −
14.11
sin 2 α
nl2
Quando la differenza dei cammini ottici è un multiplo intero k di mezza lunghezza d’onda,
14.2.1 Lamine sottili
naria≈1
la differenza δl tra i due cammini ottici si esprime
k
λ
2
= 2dnl 1 −
sin 2 α
nl2
14.12
le componenti del fronte d’onda CC' si rinforzano a vicenda (interferenza costruttiva) oppure tendono a cancellarsi a vicenda. Il comportamento è determinato dalla natura delle riflessioni che si hanno in A e in B. La fase del
raggio riflesso cambia di 180° rispetto a quello trasmesso
quando il mezzo in cui si propaga quest’ultimo ha indice
di rifrazione maggiore del mezzo da cui proviene il raggio. Se, per il caso della figura, nl ≈ 1.33, sia il raggio riflesso in A sia quello in B cambiano di 180° e si avrà interferenza positiva quando i cammini ottici differiscono
per un numero intero di lunghezze d’onda (k pari). Se invece fosse nl ≈1.6, per k pari si avrebbe interferenza negativa perché in tal caso il cambio di fase del raggio riflesso avverrebbe in A ma non in B.
Il trattamento antiriflesso a cui sono sottoposte alcune lenti consiste in una ricopertura con una lamina trasparente “a quarto d’onda”, cioè con uno spessore pari a un
quarto della lunghezza d’onda (nella lamina) della luce il
cui riflesso si vuole sopprimere. Scegliendo per la ricopertura un materiale con indice di rifrazione intermedio
tra quello dell’aria e della lente si ottiene, per incidenze
circa normali, che primo e secondo raggio riflesso abbiano intensità quasi uguale (vedi seguito) ed emergano in
opposizione di fase. È questo un esempio di filtro ottico
che agisce grazie all’interferenza.
I fenomeni basati sulla interferenza in lamine sottili
sono molteplici. Una macchia d’olio sull’acqua ha colori
cangianti sia per i diversi angoli sotto cui è osservata, sia
per variazioni dello spessore dell’olio. Alcuni visori a
cristallo liquido contengono una lamina di spessore uniforme fatta da molecole a forma di bastoncello. L’inclinazione dei bastoncelli relativamente al piano della
lamina, e quindi lo spessore della lamina, cambia per ef-
308 Capitolo 14
fetto di un cambio di temperatura. Se, per esempio, la
lunghezza d’onda della luce di cui la lamina impedisce la
riflessione passa dall’infrarosso al visibile, la zona che ha
cambiato temperatura verrà vista con una tonalità più
scura rispetto alle zone circostanti. I vetri di molti grattacieli di Dallas (Texas) sono coperti da sottili lamine di
plastica che riflettono le componenti rosa, azzurre o verdi
della luce del sole, o che assorbono una parte della luce
visibile, creando magici effetti luminosi.
Si hanno spesso superfici di vetro o altri materiali trasparenti separate da sottili strati d’aria. Nella figura si è
rappresentata una lente semisferica appoggiata su una lastra di vetro.
Dividiamo idealmente a metà lo spessore della fenditura
e pensiamola costituita da tante coppie di sorgenti puntiformi tutte distanti d/2 tra di loro. Nella direzione per la
quale lo sfasamento tra le onde che si propagano oltre la
fenditura e provenienti da una coppia vale π si ha (vedi
Equazione 14.5)
δϕ = π = 2π
In questa direzione ogni sorgente interferisce distruttivamente con la sua gemella e l’intensità è perciò nulla.
L’angolo sotto il quale non si ha propagazione di luce sarà perciò
sin ϑ min =
λ/2
N N
N
N N
Guardando dall’alto, attorno al punto di contatto tra le
due superfici si osserva una macchia nera perché i raggi
riflessi dalla superficie lente/aria e da quella, immediatamente vicina, aria/lastra differiscono di 180° e tendono
ad annullarsi. Un altro circolo nero (N) si ha quando la
distanza tra lastra e lente è pari a mezza lunghezza
d’onda; in tal caso, alla differenza di fase dovuta alle riflessioni si deve aggiungere il ritardo del cammino ottico,
maggiore di una lunghezza d’onda, del raggio che è riflesso dalla lastra. Tra circoli neri si osservano fasce luminose, dove la differenza dei cammini ottici è un multiplo dispari di mezza lunghezza d’onda. Questi cerchi
concentrici luminosi e scuri sono detti anelli di Newton.
λ
14.13
d
Per una discussione più quantitativa, dividiamo la fenditura in trattini di lunghezza dy e facciamo la somma (integrale) delle onde dai vari trattini che si propagano a un
angolo ϑ rispetto all’asse della fenditura. Indicando con y
la distanza da un estremo della fenditura (vedi figura precedente), lo sfasamento dell’onda originata in y rispetto a
quella originata in y = 0 è
δϕ ( y) =
2π y sin ϑ
λ
= ay
Sommiamo gli spostamenti delle onde secondarie che si
propagano secondo un angolo ϑ assumendo per tutte uguale ampiezza, come fatto nella 14.10. L’ampiezza
complessiva Atot è proporzionale a
1 ad
sin ad
d
Atot ∝ ∫0 cos(δϕ ( y))dy = ∫0 cos x dx =
a
a
e l’intensità luminosa è proporzionale al quadrato di tale
ampiezza
14.3 La diffrazione
Se abbiamo una sola fenditura di larghezza d investita da
un’onda piana di lunghezza d’onda λ ci aspettiamo che le
onde secondarie che si irradiano dai vari punti della fenditura interferiscano tra di loro.
y
d
ϑ
0
d sin ϑ
2λ
2
I (ϑ ) ∝ Atot
∝
sin ad 2
2π sin ϑ
con a =
λ
a
14.14
L’andamento dell’intensità I(ϑ)/I(0) in funzione di ϑ è
rappresentato per due casi: una fenditura “stretta” (con
d = 0.5λ, minimo di intensità per ϑ ≈ 90°) e una “larga”
(d = 10λ , primo minimo per ϑ ≈ 5°). Il comportamento
della fenditura è sostanzialmente descritto dall’angolo
ϑmin dato dalla 14.13, il quale indica di quanto si sparpaglino le direzioni di propagazione di un’onda piana mo-
Ottica 309
nocromatica a seguito del passaggio attraverso una fessura larga d. Quando la fessura ha spessore molto minore
della lunghezza d’onda, d << λ, dalla 14.14 si ha
I(ϑ) ≈ I(0), ossia l’onda è circolare in quanto ha uguale
intensità in tutte le direzioni.
1
d = 0.5λ
d = 10λ
.5
0
−45°
0
45°
ϑ
Viene chiamato diffrazione il fenomeno per cui un’onda
piana che incide su un’apertura di dimensioni paragonabili con la sua lunghezza d’onda si propaga poi in direzioni diverse rispetto a quella originale. La diffrazione è
un fenomeno facilmente osservabile, caratteristico della
propagazione delle onde, che è in accordo con il principio di Huygens secondo cui i punti di un fronte d’onda
vanno considerati come sorgenti di onde sferiche. La
comprensione della diffrazione consente di dare un significato preciso al concetto di “fenditura stretta” usato per
descrivere l’esperimento di Young. Nel caso in cui la
fenditura non sia “stretta” l’esperimento di Young può
essere fatto ugualmente purché ci si limiti al piccolo intervallo di angoli ϑ per cui l’intensità del raggio rifratto
sia prossima al suo valore massimo.
I fenomeni fin qui discussi si possono pensare come
dovuti all’interazione della luce con la materia. Ci aspettiamo che le cariche elettriche della materia, sottoposte al
campo elettrico oscillante E di un raggio luminoso, vibrino all’incirca nella direzione di E emettendo così onde
elettromagnetiche secondarie che producono il raggio riflesso e quello rifratto. Anche nel caso dell’interferenza e
della diffrazione si deve avere uno schermo opaco, ossia
della materia capace di assorbire completamente la luce
incidente. Si può dire che il materiale dello schermo emette una radiazione uguale a quella della luce incidente
e di fase opposta, la quale annulla completamente l’onda
elettromagnetica complessiva al di là dello schermo opaco. Interferenza e diffrazione sono perciò dovute al fatto
che, togliendo una parte di schermo, si deve togliere la
corrispondente parte di radiazione da questo generata. Da
questo punto di vista, è la schermatura incompleta, e non
la fessura, che produce l’interferenza.
14.4 Diffusione e polarizzazione
Riflessione, rifrazione, interferenza e diffrazione sono fenomeni che sembrano avere bisogno di una discontinuità,
una superficie interrotta (schermo con fessure) o una superficie che separa mezzi con proprietà differenti. Questi
fenomeni sono stati interpretati pensando alla luce come
un’onda in presenza di tale discontinuità, senza fare riferimento alla sua natura fisica. Per interpretare i fenomeni
che presentiamo in questo paragrafo non è però conveniente prescindere dalla natura della luce, anche se furono studiati prima che questa fosse nota. Utilizzeremo i risultati della teoria di Maxwell (Capitolo 11) in base alla
quale la luce è un’onda elettromagnetica trasversale, in
cui campo magnetico ed elettrico oscillano lungo direzioni perpendicolari a quella di propagazione.
z
y
direzione di
propagazione
vietata
x
onda
incidente
D
campo
elettrico
onda
diffusa
dipolo
oscillante
onda
diffusa
Penseremo la materia come costituita da dipoli elettrici D
liberi di vibrare sotto lo stimolo del campo elettrico associato a un’onda luminosa, che immagineremo essere
un’onda piana che si propaga nel verso delle y crescenti
con il campo elettrico oscillante lungo l’asse z. L’onda
incidente, proveniente da sinistra, si dice allora polarizzata linearmente lungo z (detta direzione di polarizzazione) e il piano yz si chiama piano di polarizzazione. Il
campo elettrico nella materia sarà dovuto al campo elettrico dell’onda incidente, diretto come z, sommato al
campo elettrico prodotto dai dipoli D, anch’essi diretti
come z. Poiché lungo l’asse del dipolo il campo elettrico
da questo generato è sempre parallelo a D, il campo elettrico del dipolo non potrà che oscillare nella direzione z.
Una conseguenza importante è che l’onda dovuta al dipolo oscillante non può propagarsi lungo z, che è una
310 Capitolo 14
direzione vietata dalla natura trasversale dell’onda elettromagnetica. L’oscillazione del dipolo elettrico genera
perciò onde, anch’esse polarizzate lungo z, che si propagano in tutte le direzioni del piano xy, ma non lungo z.
Nella figura precedente abbiamo rappresentato due di
queste onde secondarie: una lungo y e l’altra lungo x. Il
fenomeno per il quale un’onda luminosa che attraversa la
materia omogenea e isotropa (ossia senza discontinuità e
con uguali proprietà in tutte le direzioni) genera onde che
si propagano in direzioni diverse da quella originale si
chiama diffusione (scattering) della luce.
Supponiamo ora che l’onda incidente, sempre viaggiante lungo y, risulti dalla sovrapposizione di oscillazioni del campo elettrico lungo z ( b ) e lungo x (•).
onda diffusa
z
y
x
onda incidente
onda diffusa
La natura trasversale del fenomeno luminoso garantisce
che il fascio diffuso che si propaga lungo x sia completamente polarizzato lungo z , mentre quello diffuso lungo
z sia completamente polarizzato lungo x. Il fascio diffuso
nella direzione di incidenza (y) potrà invece avere sia oscillazioni lungo z sia oscillazioni lungo x.
In un mezzo trasparente, la radiazione diffusa in direzioni perpendicolari a quelle di incidenza ha intensità solitamente molto minore rispetto a quelle dell’onda incidente. La luminosità del cielo dipende dalla diffusione
della luce da parte dell’atmosfera; il suo colore azzurro
dipende dal fatto che, all’aumentare della frequenza della
luce, passando quindi dal rosso al violetto (vedi Capitolo
15), aumenta la percentuale di radiazione diffusa.
14.4.1 Polarizzazione per riflessione
Le considerazioni sullo stato di polarizzazione dei raggi
luminosi si possono applicare anche a un riesame dei fenomeni di riflessione e rifrazione. Supporremo i due
mezzi isotropi, ossia con le stesse proprietà fisiche lungo
qualunque direzione. Nella figura seguente abbiamo rappresentato un’onda che arriva con angolo di incidenza α
alla superficie di separazione tra il vuoto e un mezzo materiale con indice di rifrazione n, e che è polarizzata nel
piano di incidenza; ossia il campo elettrico dell’onda incidente vibra nel piano del disegno e nella direzione indicata dalle frecce doppie.
α
α'
direzione proibita se
α' + α " = π/2
vuoto
n
α″
Sia raggio riflesso sia raggio rifratto sono dovuti alle onde secondarie generate dalle oscillazioni dei dipoli elettrici del mezzo materiale. Le oscillazioni dei dipoli del
materiale devono avvenire perpendicolarmente alla direzione del raggio rifratto e devono appartenere al piano di
incidenza, non essendovi ragione per cui in un mezzo isotropo si inneschino oscillazioni perpendicolari a tale piano. Poiché anche il raggio riflesso va interpretato come
un’onda secondaria prodotta dall’oscillazione dei dipoli
del mezzo materiale (che avvengono perpendicolarmente
al raggio rifratto) si ha che la perpendicolare al raggio rifratto è una direzione di propagazione proibita per il
raggio riflesso. Per un’onda incidente polarizzata nel piano di incidenza, l’intensità del raggio riflesso si annulla
quando la somma dell’angolo di incidenza, α = α ' , e
quello di rifrazione α", è pari a 90°. Si può mostrare che,
per onde polarizzate nel piano di incidenza (||), il rapporto tra intensità luminosa riflessa Irfl(||) e intensità luminosa incidente Iinc(||) è
I rfl (||) tan 2 (α − α ")
=
I inc (||) tan 2 (α + α ")
14.15
Questa equazione traduce la legge dedotta in modo intuitivo in quanto, se α + α " = 90°, nella 14.15 l’intensità riflessa è nulla (infatti tan 90° = ∞).
Si può mostrare che, per onde polarizzate normalmente al piano di incidenza (•), la relazione tra l’intensità riflessa Irfl(⊥) e quella incidente Iinc(⊥) è
I rfl ( ⊥ ) sin2 (α − α ′′ )
=
I inc ( ⊥ ) sin2 (α + α ′′ )
14.16
Le due relazioni 14.15, 14.16 sono spesso citate come
leggi di Fresnel, in onore di Augustin-Jean Fresnel,
considerato il fondatore dell’ottica fisica per i suoi espe-
Ottica 311
rimenti sulla polarizzazione della luce. La 14.15 contiene la legge di Brewster: all’angolo di incidenza per il
quale raggio riflesso e raggio rifratto sono tra loro perpendicolari, la luce riflessa è completamente polarizzata
perpendicolarmente al piano di incidenza. L’angolo di
incidenza per cui si realizza questa condizione si chiama
angolo di Brewster, αB. La definizione data vale anche
quando la luce, anziché dal vuoto, proviene da un mezzo
materiale con indice di rifrazione n1 e si propaga poi in
un mezzo isotropo con indice di rifrazione n2.
αB αB
n1
90°
n2
Sui campi di neve o in prossimità di superfici d’acqua
nelle giornate di sole è bene usare occhiali con lenti di tipo POLAROID (vedi seguito) che, se indossati da persona in posizione eretta, sono trasparenti solo alla luce polarizzata in un piano verticale: la maggior parte della luce
riflessa dagli specchi d’acqua è polarizzata nel piano perpendicolare a quello di incidenza, ed è assorbita dalle
lenti degli occhiali. Per determinare se le lenti degli occhiali da sole hanno proprietà polarizzanti basta osservare se cambia il luccichio di uno specchio d’acqua al ruotare delle lenti.
Otteniamo ora una espressione, semplice e utile, per
l’intensità della luce riflessa quando angoli di incidenza e
rifrazione sono abbastanza “piccoli” (rispetto a 1 rad) da
poter approssimare seno e tangente con l’arco (in rad):
sin(α ± α") ≈ α ± α"≈ tan(α ± α")
α″
La legge di Snell si riscrive
Dalla figura si vede che αB e l’angolo di rifrazione corrispondente α ″ sono complementari, ossia
sin α ′′ = cos α B
La legge di Snell 14.4 perciò implica
n2 sin α B sin α B
=
=
= tan α B
sin α ′′ cos α B
n1
14.17
Poiché l’angolo di Brewster può essere misurato determinando l’angolo di incidenza per il quale il raggio riflesso
è completamente polarizzato perpendicolarmente al piano
di incidenza, la 14.17 permette di ricavare l’indice di rifrazione del secondo mezzo, anche quando non è possibile osservare il raggio rifratto. Per l’interfaccia aria-acqua
(n1 = naria ≈ 1.00, nacqua ≈ 1.33) l’angolo di Brewster è di
circa tan−11.33 ≈ 53°.
∼53°
filtro Polaroid
∼ ∼ ∼
∼
∼
∼
∼ ∼ ∼
∼ ∼
∼
∼ ∼ ∼ ∼
osservatore
∼
∼ ∼∼ ∼ ∼∼
∼
specchio di acqua
luce polarizzata
∼ ∼ ∼ ∼ ∼∼
riflettente
∼∼ ∼ ∼ ∼ ∼
n1
sin α
α
=
≈
n2 sin α " α "
e le leggi di Fresnel 14.15 e 14.16 danno lo stesso risultato per ambedue le polarizzazioni (|| e ⊥); inoltre il rapporto delle intensità riflesse e incidenti si esprime in modo
indipendente dall’angolo α << 1 rad. Ιnfatti
n2
2 1−
I rfl α − α ′′
n1
≈
=
n2
I inc α + α ′′
1+
n1
2
n − n2
= 1
n1 + n 2
2
14.18
Per esempio, per un raggio che dall’aria (n1 ≈ 1) incide
quasi normalmente sull’acqua (n2 = 1.33) la 14.18 dà
I rfl 0.33 2
≈
≈ 2%
I inc 2.33
ossia, solamente il 2% dell’intensità luminosa incidente
normalmente sugli specchi d’acqua viene riflessa.
14.4.2 Polarizzazione per rifrazione
In alcune sostanze vi sono molecole di forma allungata,
tra di loro allineate, che rispondono in modo molto diverso ai campi elettrici a seconda che essi siano paralleli
all’asse della molecola o perpendicolari a questo. L’asse
312 Capitolo 14
di allineamento delle molecole si chiama asse ottico della
sostanza e questa presenta il fenomeno della birifrangenza: indice di rifrazione e velocità della luce sono differenti per un’onda polarizzata parallelamente e per una
polarizzata perpendicolarmente all’asse ottico.
Consideriamo un raggio di luce che si propaga lungo
y e che incide normalmente su una lamina costituita da
una sostanza che ha l’asse ottico nella direzione z. Immaginiamo che il raggio incidente sia costituito da una
componente di campo elettrico vibrante lungo z e una uguale lungo x: supponiamo anche che le due componenti
di E raggiungano il valore massimo contemporaneamente. Il campo elettrico risultante è allora un vettore che è
sempre orientato come la bisettrice degli assi z e x: la luce si dice allora polarizzata linearmente lungo un asse
inclinato di 45° rispetto all’asse z e il piano zx è il piano
di polarizzazione:
E inc = ( E cos ωt ) i + ( E cos ωt ) k
raggio
incidente
z
lamina
birifrangente
asse
ottico
y
mente. Per valori generici dell’angolo di sfasamento il
campo elettrico si muove lungo un’ellisse che ha semiassi
lunghi |E cosϕ| ed |E sinϕ| (polarizzazione ellittica).
asse
ottico
Quando l’asse ottico è parallelo al piano della lamina ma
l’incidenza non è normale si ha la situazione della figura:
le componenti polarizzate parallelamente (↔) e perpendicolarmente (•) all’asse ottico vengono rifratte in direzioni differenti ed emergono da punti diversi della lamina
dando fasci distinti e polarizzati (birifrangenza).
raggio
emergente
raggio
ordinario
asse
ottico
x
z
z 45°
x
x
polarizzazione
lineare
polarizzazione
circolare
La componente del campo elettrico parallela all’asse ottico (z) impiega un tempo δt in più di quella perpendicolare per attraversare la lamina di spessore d:
δt =
raggio
straordinario
d
( n|| − n⊥ )
c
e a questo ritardo corrisponde uno sfasamento tra le due
componenti δϕ = ωδt. Perciò il campo elettrico dell’onda
emergente è del tipo
E emerg = ( E cos ωt ) i + ( E cos(ωt − δϕ ))k
Nel caso particolare in cui δϕ = 90° il campo elettrico
descrive una circonferenza nel piano xz e l’onda emergente dalla lamina si dice essere polarizzata circolar-
Ancora un’altra situazione si ha quando l’incidenza è
normale, ma l’asse ottico non è parallelo alla superficie
della sostanza birifrangente: si genera un raggio che si
propaga in direzione normale alla superficie (raggio ordinario) e uno che, violando la legge di Snell, si muove in
direzione diversa dalla normale (raggio straordinario).
I fenomeni legati alla birifrangenza e alla polarizzazione sono molteplici e sono dovuti a proprietà microscopiche della materia. I polarizzatori sono dispositivi
basati su materiali birifrangenti che filtrano un raggio luminoso emettendo luce polarizzata in una direzione voluta: possono operare per assorbimento, interferenza o per
riflessione totale del raggio rifratto che si vuole eliminare. La più famosa sostanza birifrangente è un cristallo naturale, il feldspato d’Islanda, un carbonato di calcio già
studiato da Huygens.
Per studiare come una sostanza modifichi lo stato di
polarizzazione della luce si utilizza il semplice schema di
analizzatore riportato in figura.
Ottica 313
14.5.1 Specchi sferici
Nella figura, Q è il punto centrale di una calotta riflettente, porzione di una sfera di raggio r e centro C.
La luce passa un primo polarizzatore, attraversa la sostanza e quindi incide su un secondo polarizzatore orientato perpendicolarmente al primo (polarizzatori incrociati). L’osservatore può essere raggiunto dalla luce solo se
la sostanza ha cambiato la polarizzazione della luce che
l’ha attraversata.
Alcune sostanze hanno la proprietà di ruotare di un
certo angolo “verso destra” (sostanze destrogire) o “verso sinistra” (sostanze levogire) la direzione di polarizzazione della luce emergente; queste sostanze si dicono otticamente attive e vengono caratterizzate dal valore
dell’angolo di cui bisogna ruotare il secondo polarizzatore per ottenere la completa estinzione della luce osservata. Spesso le forme levogire e destrogire di un composto
vengono prodotte in quantità circa uguali durante una reazione chimica, ma hanno a volte proprietà differenti, in
particolare dal punto di vista farmacologico e biochimico. Le deformazioni dei nascituri prodotte negli anni Sessanta dal Talidomide (un anti-nausea usato in quel periodo) sono dovute esclusivamente a una delle due forme
speculari del principio attivo.
14.5 Ottica geometrica
L’ottica geometrica descrive i percorsi dei raggi di luce
in sistemi che obbediscono alle leggi della riflessione e
della rifrazione. I sistemi trattati dall’ottica geometrica
elementare consistono di calotte sferiche(☯) riflettenti o
rifrangenti. La perpendicolare al centro della calotta è
detta asse ottico, concetto questo che non va confuso con
quello di asse ottico di una sostanza birifrangente.
L’ottica geometrica elementare suppone che i raggi luminosi formino angoli “piccoli” con l’asse ottico e non siano mai “troppo” distanti dallo stesso. Per trattare situazioni meno ideali (superfici non sferiche e raggi qualsiasi) occorre una matematica specializzata, in buona parte
sviluppata nel secolo scorso da William Hamilton.
(☯) Una superficie piana può essere pensata come il caso
limite di una calotta sferica di raggio infinito. La scelta delle
superfici sferiche ha una motivazione di ordine pratico perché è
relativamente facile realizzare calotte sferiche, o piane, mediante molatura manuale di materiali duri e rifrangenti quali i comuni vetri.
Q'
ϑ
ϑ
r
ho
2ϑ
ϑ
C
F
Q
Dimostriamo innanzitutto che ogni raggio luminoso parallelo all’asse ottico (QC) e distante da questo molto
meno del raggio (ho<<r) incrocia l’asse ottico in un punto
F detto fuoco con
| QF| ≡ f ≈
r
2
Poiché il rapporto tra lato e seno dell’angolo opposto è
costante in un triangolo, dal triangolo CFQ' si ha
CQ'
CF
CF
r
=
⇒
=
sin( π − 2ϑ ) sin ϑ
sin 2ϑ sin ϑ
14.20
Per ho<<r si ha
sin ϑ =
ho
2h
, sin 2ϑ ≈ o
r
r
e la 14.20 diventa
| CF| ≈
r
r
⇒| QF| ≡ f ≈
2
2
14.21
Poiché la distanza |QF| non dipende da ho, tutti i raggi paralleli all’asse ottico, e abbastanza “vicini” a questo, vengono riflessi in un punto F dell’asse ottico detto fuoco.
Costruiamo ora l’immagine I di un punto O (“oggetto”) dell’asse ottico prodotta dallo specchio concavo di
centro in C e di raggio |QC| = r. Qui e nel seguito il punto
I viene trovato come intersezione di due raggi luminosi, o
dei loro prolungamenti, uscenti da O. Un raggio è scelto
lungo l’asse ottico, e viene riflesso lungo questo; il secondo raggio fa un piccolo angolo α con l’asse ottico,
raggiunge lo specchio in Q' e il raggio riflesso da Q' interseca l’asse ottico in I.
314 Capitolo 14
Q′
α
O
ε
ε
α+2ε
C α+ε
I
Q
di
do
Indichiamo per il momento con do la distanza |QO| e con
di la distanza |QI|. Un legame tra queste due distanze si
può trovare applicando il teorema dei seni ai due triangoli
OQ'Q e IQ'Q per esprimere la lunghezza del comune lato
Q'Q. Essendo per ipotesi gli angoli α ed ε piccoli, possiamo porre
sin α ≈ α
sin ε ≈ ε
$
$ Q ≈1
sin OQ' Q ≈ sin IQ'
sin(α + 2ε ) ≈ α + 2ε
e ottenere
d o α ≈ d i (α + 2ε ) ⇒ d o ≈ d i (1 + 2ε / α )
14.22a
l’oggetto in I, l’immagine si forma in O (principio di reversibilità del cammino ottico). Notiamo che, nell’esempio trattato, le distanze do di e f possono essere interpretate come le ascisse (in questo caso positive) di oggetto,
immagine e fuoco sull’asse ottico con origine in Q e diretto verso sinistra.
Prima di mostrare che la relazione 14.23 è vera anche
nel caso in cui fuoco e/o immagine abbiano ascisse negative, costruiamo l’immagine del punto O quando questo è
spostato, rispetto al caso precedente, a una distanza
dall’asse ottico piccola rispetto a r: ho << r. Si può allora
assumere (ma si può anche facilmente dimostrare) che
l’ascissa del punto immagine I sarà ancora data dalla
14.23. Il nostro scopo è quello di trovare la distanza (con
segno) del punto I dall’asse ottico. D’ora in poi rappresenteremo oggetto e immagini con frecce normali all’asse
ottico; la freccia dell’oggetto verrà sempre orientata verso l’alto e O avrà ordinata positiva (ho > 0). L’immagine
sarà “diritta” se l’ordinata di I sarà anch’essa positiva e
sopra l’asse ottico; sarà “rovesciata” se hi < 0. Per costruire I mandiamo da O un raggio parallelo all’asse ottico,
che verrà riflesso attraverso il fuoco F; mandiamo poi un
secondo raggio attraverso il fuoco F, il quale verrà riflesso parallelamente all’asse ottico.
Poiché dal disegno si ha |CO| = |QO| −|QC| = do − r, il
teorema dei seni applicato al triangolo OQ'C permette di
ricavare il legame tra α ed ε:
| OC|
ε
≈
| CQ' |
α
⇒
do − r
ε
≈
r
α
⇒
do − r ε
≈
r
α
14.22b
Facendo sistema tra la 14.22a e la 14.22b si può eliminare ε/α, un risultato molto importante in quanto garantisce
che tutti i raggi con piccola inclinazione rispetto all’asse
ottico si incontrano nello stesso punto I:
ε
d o = d i 1 + 2 α
do − r = ε
r
α
⇒
do + di =
ho−hi
Q'
F
Q
−hi
O'
Q"
I(di,hi) F'
f
Dalla similitudine dei triangoli FQ"F' e OQ"O' si ha
dodi
r/2
Mediante la 14.21 questa equazione può essere messa
nella utilissima forma
1
1
1
+
=
do di
f
O(do,ho)
14.23
Questa equazione è la relazione fondamentale degli
specchi sferici. Essa mostra che la distanza di oggetto e
immagine intervengono in modo simmetrico: ponendo
ho − hi
−h
| OO' |
| FF' |
≈
=
≈ i
do
| O' Q"| | F' Q"|
f
Eliminando in questa equazione f mediante la 14.23 si ottiene l’espressione per l’ingrandimento, ossia per il rapporto tra altezza dell’oggetto e altezza (con segno)
dell’immagine:
hi
d
=− i
ho
do
14.24
Ottica 315
Nel caso del disegno, l’ingrandimento è negativo, ossia
l’immagine è rovesciata, e in valore assoluto è minore di
1 (immagine rimpicciolita). Utilizzando la reversibilità
dei cammini ottici, possiamo concludere che se l’oggetto
si fosse trovato tra fuoco e centro C (dove si trova I nella
figura), la sua immagine sarebbe stata rovesciata e ingrandita.
Prima di illustrare la regola dei segni degli specchi,
trattiamo qualitativamente due altri casi utilizzando la
tecnica di costruzione dell’immagine appena impiegata.
Specchio concavo e oggetto tra fuoco e centro della calotta (0 < do < f).
I
O
Q
F
I due raggi uscenti da O dopo la riflessione divergono. I
prolungamenti (tratteggiati) di questi raggi si incontrano,
oltre lo specchio, in un punto con distanza negativa:
di < 0. La 14.23 vale ancora e l’ingrandimento della
14.24 è maggiore di 1, confermando quello che si vede
dalla figura, ossia che l’immagine è diritta e ingrandita.
Per esprimere il fatto che l’immagine non è punto di incontro di raggi reali si dirà che in questo caso si ha una
immagine virtuale.
Nel caso dello specchio convesso il fuoco si trova a
“destra” di Q e ha ascissa negativa. Anche l’immagine si
trova a destra di Q (di < 0), sul prolungamento dei raggi
reali (immagine virtuale).
O
I
Q
F
Si può provare che anche in questo caso vale la 14.23
(con f e di negativi) e che, per la 14.24, si ha sempre una
immagine diritta e rimpicciolita (come è evidente dalla
figura precedente). Per gli specchi si assume come positivo il semipiano in cui è collocato l’oggetto e che contiene
i raggi “reali”, sia incidenti sia quelli riflessi.
La regola dei segni per gli specchi
Gli esempi precedenti indicano che le 14.23 valgono in
tutte le condizioni pur di prendere le distanze dall’asse
ottico (ordinate) e le ascisse di Q, I, F con il segno corretto. Adotteremo per questo le seguenti convenzioni, già illustrate negli esempi precedenti:
• la distanza do dell’oggetto da Q è positiva quando
l’oggetto è a sinistra dello specchio (dove solitamente
lo poniamo) e negativa in caso contrario;
• la distanza di dell’immagine è positiva se è a sinistra
di Q, ossia nello stesso semipiano di O e all’incrocio
dei raggi riflessi; si parla in tal caso di immagine reale. La distanza di è negativa se l’immagine si trova a
destra di Q, sul prolungamento dei raggi riflessi; si
parla in tale caso di immagine virtuale;
• le altezze di oggetto e immagine vengono lette a partire dall’asse ottico lungo un asse orientato verso la
parte superiore del foglio; in genere si assume ho positivo e rappresentiamo l’oggetto con una freccia orientata verso l’alto. L’altezza hi dell’immagine sarà
negativa se I si trova nel semipiano opposto a quello
di O rispetto all’asse ottico;
• l’ingrandimento è definito dalla 14.23, ed è negativo
quando l’immagine è capovolta;
• la distanza del fuoco f è positiva se F si trova nello
stesso semipiano di O; si ha allora uno specchio concavo.
Le formule 14.23 e 14.24 valgono anche nel caso dello
specchio piano, per il quale il raggio di curvatura e la distanza focale f tendono all’infinito (1/f → 0):
1
1
+
= 0 ⇒ d o = −d i
do di
⇒ immagine virtuale
do
h
= − o ⇒ ho = hi
di
hi
⇒ immagine diritta
14.5.2 Il diottro sferico
Un mezzo con indice di rifrazione n1 è separato da un
mezzo con indice n2 mediante una calotta sferica di raggio r. Tale sistema viene chiamato diottro sferico. Come in precedenza, indichiamo con Q il centro della calotta e costruiamo l’immagine di un punto O posto sull’asse
ottico (che congiunge Q con il centro C della sfera) supponendo che i raggi che si dipartono da O facciano un
316 Capitolo 14
piccolo angolo con l’asse ottico e siano diffratti dalla superficie sferica.
n1
do
Q′
ϑ1
ϑ2
ϑ2
β
α
O
n2
Q
di = f 2 =
γ
C
r
Poiché la distanza dell’immagine non dipende dall’inclinazione α del raggio, tutti i raggi uscenti da O e formanti
un piccolo angolo convergono in un solo punto a distanza
di da Q data dalla 14.25. Per d o → ∞ il punto I tende al
fuoco F2 la cui distanza da Q vale
I
14.26a
ed è positiva nel caso della figura in cui n2 > n1 e la superficie è convessa dalla parte dell’oggetto (r > 0). Quando l’oggetto si trova nel fuoco F1 il raggio viene rifratto
parallelamente all’asse ottico; o anche
di
Nella figura abbiamo indicato direttamente le convenzioni di segno che adottiamo in questo caso. L’ascissa di O è
positiva se O si trova a sinistra di Q nel mezzo 1. Il raggio di curvatura r è positivo se C si trova nel mezzo 2 (a
destra di Q), ossia se la superficie sferica vista dal mezzo
1 è convessa; l’ascissa dell’immagine di è positiva se I è
nel mezzo 2 a destra di Q e sul raggio rifratto. Se α è piccolo, anche gli angoli di incidenza (ϑ1), di rifrazione (ϑ2)
e gli angoli β e γ indicati in figura saranno piccoli e varranno le seguenti relazioni:
do
α
r
d
r
β≈ oα
rβ ≈ d i γ ⇒ γ ≈
di
di
do
ϑ1 = α + β ≈ α 1 +
r
do do
−
ϑ2 = β − γ = α
di
r
d i → ∞ ⇒ d o = f1 =
n1
r
n2 − n1
14.26b
La costruzione dei due fuochi è mostrata nella figura seguente:
n1
d o α ≈ rβ ⇒ β ≈
n2
Q
F1
f1
f2
Si noti dalle 14.26 che le due distanze focali sono positive o negative entrambe. Utilizzando le espressioni 14.26
dei fuochi la 14.25 può essere riscritta nella forma:
Le prime due sono modi approssimati per esprimere la
lunghezza del segmento Q'Q quando è lecito sostituire alla tangente il valore dell’angolo espresso in radianti; le
ultime due discendono da relazioni esatte tra supplementare dell’angolo di un triangolo (CQ'O e CQ'I) e somma
degli altri due angoli. Gli angoli di incidenza e di rifrazione sono legati dalla legge di Snell, che si può riscrivere sostituendo gli angoli ai seni:
do do
do
n1ϑ1 ≈ n2ϑ 2 ⇒ n1α 1 +
−
≈ n2 α
r
di
r
Dividendo per αdo e riorganizzando i termini si ottiene la
relazione fondamentale del diottro sferico:
n1 n 2 n 2 − n1
+
=
do di
r
n2
r
n2 − n1
14.25
f1 f 2
+
=1
do di
14.27
La costruzione geometrica dell’immagine del diottro è
mostrata per il caso in cui tutte le distanze nella 14.27
siano positive.
n1 n2
Q'
O
F2
ho
F1
Q
−hi
Q"
I
Ottica 317
Da questa figura e dall’espressione delle distanze focali si
ricava facilmente l’espressione dell’ingrandimento semplicemente assumendo che le ascisse dei punti Q, Q' e Q"
possano essere considerate coincidenti:
hi
f d
=− 1 i
ho
f 2 do
14.28
L’occhio umano è una palla di umor vitreo (n ≈ 1.4) con
r ≈ 1.2 cm. In base alla 14.26a la distanza tra punto Q
(dove è situata la pupilla) e F2 è di 3.6 cm, cioè maggiore
della distanza pupilla-retina, pari a 2r ≈ 2.4 cm. Il cristallino è una lente regolabile tra pupilla e globo oculare
(vedi seguito) che permette che un oggetto distante
(do → ∞) produca sulla retina una immagine reale.
Come applicazione delle leggi del diottro, consideriamo un oggetto (freccia nera) in acqua (n1 = 1.333) separato da un superficie piana (r = ∞) dall’aria (n2 = 1).
Per la 14.25 con r → ∞, l’immagine (freccia più chiara) si
trova a una distanza dalla superficie |di| minore di quella
reale do. Inoltre di è negativa, e quindi l’immagine si
forma nel mezzo 1. Nella figura è indicata la costruzione
dei raggi che mostra come i prolungamenti dei raggi in
aria si incrocino più vicino alla superficie rispetto ai raggi
reali provenienti dall’oggetto. Lo stesso risultato poteva
essere trovato direttamente prendendo in considerazione
angoli di incidenza piccoli e applicando la legge di Snell
(vedi Esercizio R14.5).
n1=1.33
n2=1
do
−d i
14.5.3 Le lenti sottili
Una lente con indice di rifrazione n in aria può essere
pensata come una successione di due superfici diottriche
di raggio (con segno!) r1 e r2. L’immagine di un oggetto
distante do dalla prima superficie si forma a una distanza
d 'i da questa pari a (vedi 14.25 con n1 = 1, n2 = n)
n
n −1 1
=
−
d 'i
r1
do
14.29a
Questa immagine va considerata come l’oggetto per la
seconda superficie; se d 'o è la distanza (con segno) di
questa immagine dalla seconda superficie, questa formerà
a sua volta un’immagine a distanza di data da (vedi 14.23
con n1 = n, n2 = 1)
n
1− n 1
=
−
d 'o
r2
di
14.29b
La differenza tra i valori assoluti di d 'i e d 'o è pari allo
spessore della lente, ma le due quantità hanno segno opposto in quanto un oggetto ha distanza positiva quando è
a sinistra della superficie mentre una immagine ha distanza positiva se è a destra della stessa. Se la lente è sottile,
possiamo trascurare il suo spessore e porre approssimativamente d 'i ≈ −d 'o Sommando membro a membro le equazioni 14.29 si ha
0=
n −1 1 1− n 1
−
+
−
r1
do
r2
di
o anche
1 1 1
1
1
+
= (n − 1) − ≡
do di
r1 r2 f
14.30
Questa è la cosiddetta equazione dei fabbricanti di lenti:
a differenza del caso del diottro, se i mezzi iniziale e finale sono gli stessi, vi è ora un’unica distanza focale comune ai due fuochi F1 (dalla parte di O) e F2. La distanza
focale f è determinata dall’indice di rifrazione della lente
e dai raggi di curvatura, presi con il loro segno(☯), delle
superfici della lente.
L’equazione 14.30 è formalmente uguale alla 14.22:
le proprietà di specchi e lenti sono molto simili e sono
ambedue descritti dalla distanza focale f. Una differenza
sta nella convenzione dei segni: la distanza focale è positiva se l’immagine dell’oggetto all’infinito si forma a sinistra nel caso degli specchi (specchi concavi) e a destra
(☯) In alcuni testi si segue una convenzione diversa sui se-
gni e il raggio di curvatura della seconda superficie è assunto
con il segno cambiato. Nel caso di una lente che presenta
all’aria due superfici convesse, il primo raggio di curvatura è
positivo e il secondo negativo per chi segue il percorso di un
raggio attraverso la lente; la sua distanza focale è perciò legata
alla somma dei reciproci dei valori assoluti dei due raggi di
curvatura.
318 Capitolo 14
nel caso delle lenti (lenti convesse); la distanza dell’immagine è positiva (immagine reale) se questa si forma sul
raggio riflesso (ossia a sinistra) per gli specchi e a destra
per le lenti (ossia sul raggio rifratto).
do
di
immagine
Specchio concavo e lente convessa (f > 0)
do > 2f
f < di < 2f
reale, invertita, più piccola
do = 2f
di = 2f
reale invertita, uguale
f < do< 2f
di > 2f
reale, invertita, più grande
do < f
di < 0
virtuale e diritta
Specchio convesso e lente concava
∀ do
di < do
virtuale, diritta, più piccola
Due esempi di costruzione dell’immagine di una lente
sono dati in figura: si invia dalla punta della freccia che
rappresenta l’oggetto un raggio parallelo all’asse ottico
che passerà per il fuoco principale F2 (a destra se f > 0);
un secondo raggio può essere disegnato tracciando la retta per il centro C della lente.
F2
F1
Q
immagine
reale
ra (diametro o altezza), che di solito si esprime come frazione della sua distanza focale: una lente f/5.5 ha un distanza focale pari a 5.5 volte la sua altezza. La distanza
focale si esprime spesso in diottrie, un numero pari al reciproco della distanza focale espressa in metri:
diottrie =
1
f [metri]
Con un procedimento simile a quello utilizzato per ricavare la formula delle lenti sottili si trova che la distanza
focale complessiva f di un sistema composto da due lenti
vicine (con distanze focali f1 e f2) è il reciproco della
somma dei reciproci
1
1
1
=
+
f
f1 f 2
14.31
ossia
diottrie complessive = diottrie(1) + diottrie(2)
14.5.4
Il microscopio e il limite
di risoluzione
Il microscopio è un sistema ottico formato, in linea di
principio, da due lenti convesse: l’obiettivo, vicino
all’oggetto da osservare, e l’oculare, vicino all’occhio
dell’osservatore.
obiettivo
immagine
virtuale
F2
F1
Q
Come per gli specchi, l’ingrandimento di una lente è descritto dalla 14.23, che vale con le convenzioni sui segni
delle altezze espresse in quella occasione: un’immagine
virtuale è sempre diritta (con altezza positiva) mentre una
immagine reale è sempre invertita. Occhio umano, cineprese e macchine fotografiche sono sistemi ottici che
producono su una superficie sensibile (retina o pellicola
fotosensibile) un’immagine reale che può provenire direttamente dall’oggetto oppure da un’immagine (reale o virtuale) prodotta da un altro sistema ottico.
Un parametro importante di una lente è la sua apertu-
oculare
F1
O
ϕ
I2 I1
osservatore
F2
L’oggetto O è prossimo al fuoco dell’obiettivo che forma
un’immagine I1 reale e ingrandita in prossimità dell’oculare; questo agisce come una lente di ingrandimento dando l’immagine virtuale I2. Per poter essere vista distintamente, questa immagine si deve formare a una distanza
dall’occhio di circa 25 cm.
L’ingrandimento di un microscopio può essere definito come il rapporto tra altezza dell’immagine I2 (in valore
assoluto) e altezza dell’oggetto. L’ingrandimento di un
microscopio può in linea di principio essere arbitrariamente grande ma vi è un limite al di là del quale la riso-
Ottica 319
luzione, ossia l’inverso della minima distanza tra due
punti dell’oggetto che sono visti come separati, non aumenta più. Per discutere questo punto, supponiamo che
l’oggetto sia costituito da una alternanza di strisce opache
e trasparenti, perpendicolari al piano del disegno, spesse
d/2 e parallele tra di loro.
d
ϕ
ϑ1
ϑ2
λ
L’illuminazione sia fornita da un fascio di luce diretto
come l’asse ottico con lunghezza d’onda λ = 5(10−7) m.
L’oggetto è un reticolo di diffrazione, ossia una schiera di
fenditure a distanza d una dall’altra. Come visto nel Paragrafo 14.2, la schiera emette intensi fasci di luce in direzioni inclinate, rispetto all’asse ottico, di angoli pari a
kλ
ϑ k = sin −1 con k = 0, ±1, ±2, ...
d
14.32
(vedi 14.6a). Se l’obiettivo è in grado di raccogliere almeno parte del fascio che forma l’angolo ϑ1, l’osservatore vedrà nella loro interezza due bande nere attorno a
una banda chiara centrale; ossia vedrà in modo distinto
due oggetti (righe opache) a distanza d/2 l’uno dall’altro.
Detto ϕ l’angolo di apertura dell’obiettivo (vedi figura
precedente) si ha una risoluzione pari a 2/d quando
ϕ = ϑ 1 ⇒ sin ϕ =
λ
opportuni rivelatori, si può usare una radiazione con lunghezza d’onda minore di quella della luce visibile, ma
occorre rinunciare ai nostri occhi come strumento di rivelazione. Inoltre, per lunghezze d’onda della radiazione
elettromagnetica minori delle dimensioni atomiche l’indice di rifrazione di tutti i materiali è praticamente uguale
a 1, ed è di fatto impossibile costruire un sistema rifrangente.
Il microscopio elettronico supera queste difficoltà utilizzando fasci di elettroni anziché la radiazione elettromagnetica: a un elettrone con quantità di moto p è associata una lunghezza d’onda λ = h/|p| (vedi Capitolo 15)
che può essere facilmente resa molto minore delle dimensioni atomiche; la traiettoria dell’elettrone può essere
controllata mediante campi elettrici e magnetici che hanno la stessa funzione delle lenti nell’ottica convenzionale.
Si è visto che, oltre che dalla lunghezza d’onda, la risoluzione dipende dall’angolo di apertura dell’obiettivo.
Con l’aiuto della formula 14.13 per la diffrazione mostriamo adesso che l’apertura d di un sistema ottico determina la sua risoluzione angolare, ossia la minima inclinazione tra due raggi che possono essere distinti. Un
fascio di luce che incide normalmente su una fessura larga d viene diffratto e si estingue completamente solo nella direzione che forma un angolo ϑ1= λ/d con la normale
alla fessura. Perciò fasci di luce che formano un angolo
minore di ϑ1 producono su uno schermo comunque lontano immagini parzialmente sovrapposte della fessura.
retina
pupilla
d
d
L = 2.4 cm
fovea
centrale
ossia
risoluzione =
2 2 sin ϕ
=
d
λ
14.33
Poiché sinϕ ≤ 1, la risoluzione è al massimo pari al reciproco di mezza lunghezza d’onda: se entro l’angolo di
apertura dal reticolo all’obiettivo cade solamente il fascio
luminoso centrale si vedrà un’illuminazione abbastanza
uniforme anziché un susseguirsi di bande chiare e scure
che riproducono la struttura del reticolo.
La 14.33 afferma che la risoluzione aumenta al diminuire della lunghezza d’onda. Per questo molti microscopi prevedono la possibilità di interporre un olio trasparente tra campione e obiettivo: poiché la lunghezza d’on-da
è inversamente proporzionale all’indice di rifrazione
dell’olio, la risoluzione aumenta di nolio. Disponendo di
Nella figura si danno gli elementi geometrici per il calcolo della risoluzione angolare dell’occhio umano:
l’apertura d è pari al diametro della pupilla, circa 5 mm;
la lunghezza d’onda della luce nell’umor vitreo cambia
con il colore, ma si può assumere un valor medio
λ = 5(10−7) m, da cui si ricava ϑ1 ≈ 10−4 rad. Poiché la
distanza pupilla-retina è L ≈ 2.4 cm, sulla retina non si
possono avere immagini separate più di
Lϑ1 ≈ 2.4(10−6) m
Questo è il tipico diametro dei coni ottici nella fovea cen-
320 Capitolo 14
trale. Ancora una volta si deve concludere che l’evoluzione conosce benissimo la fisica.
Anche l’ottica geometrica qui sviluppata è molto intuitiva e richiede semplici (ma approssimate) costruzioni.
L’equazione da ricordare per gli specchi e le lenti sottili è
la stessa:
1
1
1
+
=
do di
f
Riassunto
Questo capitolo si è aperto con il dibattito sulla natura
corpuscolare od ondulatoria della luce: sembra che Huygens batta Newton su tutta la linea. Il modello ondulatorio spiega con elegante semplicità riflessione, rifrazione,
interferenza e diffrazione; anche i complessi fenomeni di
polarizzazione, birifrangenza e attività ottica sono interpretabili nel quadro del modello ondulatorio, benché possano essere capiti a fondo solo mediante le equazioni di
Maxwell e nozioni di struttura della materia. La storia
dell’ottica non è però finita: proseguirà nel prossimo capitolo dove Newton si prende, in qualche modo, una rivincita.
dove di è negativo se l’oggetto è virtuale, ossia sul prolungamento dei raggi riflessi o rifratti; la distanza focale è
negativa quando l’immagine di un oggetto all’infinito in
prossimità dell’asse ottico è virtuale; positiva quando
l’immagine è reale.
Un punto in cui ottica fisica e ottica geometrica si incontrano è quello riguardante la risoluzione del microscopio e, in generale, di sistemi diottrici quale l’occhio
umano. Il trattamento dell’interferenza consente di porre
su base quantitativa l’intuizione che il limite di risoluzione e la lunghezza d’onda sono quantità tra loro legate.
ESERCIZI RISOLTI ______________________________________________________________
Esercizio R14.1 L’equazione per un raggio luminoso che si propaga in un vetro lungo la direzione y è
[
]
E x ( y , t ) = E x cos 2π ( y / λ ) − νt con λ = 6 × 10 −7 m e ν = 3 × 1014 Hz
L’indice di rifrazione del vetro è di circa
(A) 1.333 (B) 1.00 (C) 2.789 (D) 1.29 (E) 1.67
Soluzione Dall’equazione dell’onda si ricava la velocità di propagazione del raggio
v = λν = 1.8 × 108 m/s
Il rapporto tra la velocità della luce nel vuoto c ≈ 3×108 m/s e v dà l’indice di rifrazione
n = c/v ≈ 1.67
Esercizio R14.2 Guardando di giorno il cielo dal fondo di una piscina (n = 4/3), si vede la superficie
dell’acqua bene illuminata entro un cono che ha un angolo di apertura pari a circa
(A) 90°
(B) 45°
(C) 97 10' (D)48° 35' (E) indeterminato
α
β
Ottica 321
Soluzione L’angolo richiesto è pari al doppio dell’angolo di rifrazione β in corrispondenza di un angolo
di incidenza α pari a 90° per la luce proveniente dall’aria. Si ha
sin α 4
3
=
⇒ sin β = ⇒ β = 48° 35'
sin β 3
4
La risposta è perciò 97° 10'
Esercizio R14.3 Una telecamera è situata sul bordo di una piscina a una altezza di due metri rispetto al pelo
dell’acqua. Quando la telecamera punta verso la piscina formando un angolo di 30° con la
verticale, nel centro del suo campo visivo è inquadrata una moneta che giace sul fondo della
piscina, a due metri sotto il pelo dell’acqua.
x1
x2
h1
α
h2
β
Se l’indice di rifrazione dell’acqua è n = 4/3, la distanza orizzontale tra moneta e bordo della
piscina è pari a circa
(A) 2.00 m (B) 1.96 m (C) 1.62 m (D) 2.31 m (E) 1.94 m
Soluzione I dati geometrici del problema sono h1 = h2 = 2 m e α = 30°. L’angolo di rifrazione β si
ottiene da
sin β =
sin α 3
= ⇒ β = 22° 01'
4/3 8
La distanza orizzontale della moneta sul fondo è
d = x1 + x 2 = h1 tan α + h2 tan β = 1155
.
+ 0.8093 m ≈ 1.96 m
Esercizio R14.4 Un raggio di luce si propaga in acqua (n1 = 4/3) e in un piano verticale raggiunge la faccia
laterale del cubo della figura con un angolo di incidenza α = 52° 19'. Il raggio rifratto nel cubo raggiunge la faccia superiore di questo con angolo di incidenza β pari a quello limite che
produce riflessione totale.
n1
n2
322 Capitolo 14
L’indice di rifrazione n2 del materiale costituente il cubo è di circa:
(A) 1.27 (B) 1.33 (C) 1.53 (D) 1.70 (E) 1.89
Soluzione Le condizioni di riflessione totale alla faccia superiore e di rifrazione sulla faccia laterale
portano al sistema
tan β =
n2 sin β = n1 sin 90° = n1
⇒
n1 sin α = n2 sin( 90°− β ) = n2 cos β
sin β =
2
cos 2 β
1
sin α =
sin 2 β
sin α ⇒
2
n1
sin 2 β = n1
n2
n22
Da qui si ottiene
sin 2 α =
n22 − n12
⇒ n2 = n1 sin 2 α + 1 ≈ 170
.
n12
Si noti che l’indice di rifrazione del cubo (probabilmente un tipo di vetro) deve essere maggiore di quello dell’acqua per avere riflessione totale. Poiché sinα ≤ 1, tale indice di rifrazione deve essere al massimo pari a n2 2 ≈ 189
. per consentire di raggiungere l’angolo limite di
riflessione totale.
Esercizio R14.5 Guardando dall’alto una capocchia di spillo sul fondo di un recipiente riempito di olio minerale (nolio = 1.47) fino a una altezza di 10 cm dal fondo, la profondità apparente a cui si vede
la capocchia di spillo è di circa
(A) 10 cm (B) 14.7 cm (C) 7.1 cm (D) 6.8 cm (E) 4.6 cm
Soluzione Il problema si può risolvere sia con la formula del diottro con raggio di curvatura infinito sia
con il seguente ragionamento: dal punto O dove è situato l’oggetto si dipartono raggi che
formano con la verticale angoli α molto piccoli e vengono rifratti in aria secondo angoli β che
sono anch’essi “piccoli”, ossia molto minori di 1 rad.
aria
A
P
β
n = 1.47
α
I
O
Si ha perciò
tan α ≈ sin α
tan β ≈ sin β
mentre per la legge della rifrazione
n=
sin β
= 147
.
sin α
Dai triangoli APO e API si ricava
Ottica 323
AP = AO tan α ≈ AO sin α
AI
sin α
1
⇒
=
⇒ AI = 10
≈ 6.8 cm
β
β
AP
=
AI
tan
≈
AI
sin
β
AO
sin
.
147
Esercizio R14.6 La risoluzione angolare dell’occhio umano è pari a circa 0.0003 rad. Qual è, all’incirca, la
minima distanza tra le due fenditure di un esperimento di Young, nel quale si utilizza luce con
lunghezza d’onda λ = 589 nm, che consenta all’occhio di vedere direttamente le frange di interferenza?
(A) 1.0 mm (B) 2.0 mm (C) 3.14 mm (D) 16 nm (E) 4.1 m
Soluzione Detta d la distanza tra le fenditure, due consecutive frange di interferenza sono viste sotto
l’angolo ∆ϑ ≈ λ/d. Posto ∆ϑ = 0.0003 rad si ottiene d ≈ 1.96 mm ≈ 2 mm
Esercizio R14.7 Con un occhio a 1 cm sopra il pelo dell’acqua si osserva la superficie liscia del mare investita
al tramonto dalla luce quasi radente del Sole, la quale ha lunghezza d’onda pari a circa 0.5
nm. Approssimativamente, qual è l’angolo minimo formato con l’orizzontale dalla direzione
dei raggi solari per il quale si ha interferenza distruttiva tra raggi solari diretti e raggi riflessi
dall’acqua?
(A) 1° (B) 5' (C) 30" (D) 5" (E) < 1"
Soluzione La geometria del problema è la seguente
A
90°−2ϑ
ϑ
O
ϑ
h = 1 cm
P
Poiché nella riflessione in P il raggio cambia la sua fase di 180°, si avrà interferenza negativa
quando le distanze |PO| e |AO| differiscono di un multiplo intero di lunghezze d’onda. Tali distanze si possono esprimere in funzione di h e ϑ alla seguente maniera:
PO =
h
sin ϑ
AO = PO sin( 90°−2ϑ ) ⇒ PO − AO =
h
(1 − cos 2ϑ )
sin ϑ
L’angolo minimo si ha quando la distanza tra |PO| e |AO| è pari a una lunghezza d’onda. Poiché l’angolo ϑ è per ipotesi “piccolo” (molto minore di 1 rad) si ha:
λ = PO − AO = h
1 − cos 2ϑ
λ
= 2h sin ϑ ≈ 2hϑ ⇒ ϑ =
≈ 5"
sin ϑ
2h
Esercizio R14.8 La superficie sferica di una lente con indice di rifrazione n = 1.667 è appoggiata su di un
piano riflettente; la lente è investita normalmente al piano da una radiazione con λ = 700 nm.
Si osservano vari anelli scuri di Newton attorno alla macchia nera centrale e il diametro del
quindicesimo anello scuro è d15 = 7.67 mm. Il raggio di curvatura R della superficie sferica
vale circa
(A) 1.67 m (B) 1.40 m (C) 38.3 cm (D) 19.6 cm (E) 3.14 cm
324 Capitolo 14
C
R
P
A
s15
d15
Soluzione Indicata con s15 la distanza tra le due superfici in corrispondenza al 15-esimo anello la condizione di interferenza negativa è
15λ = 2 s15
in quanto vi è un cambiamento di fase di 180° nella riflessione aria/vetro/aria. Utilizzando il
teorema di Pitagora applicato al triangolo CAP si trova una relazione tra R, d15 e s15
(
R 2 = R − s15
) 2 + (d15 / 2) 2 ⇒ 2 Rs15 = 15λR = s152 + d152 / 4 ≈ d152 / 4
dove si è utilizzato il fatto che, dai dati, s15 << d15 . Si arriva così a
(
)
2
7.67 × 10 − 3
d2
R = 15 =
≈ 1.40 m
60λ 60 × 7 × 10 − 7
(
)
Esercizio R14.9 L’angolo di incidenza per il quale la luce riflessa dalla superficie di un lago (nacqua = 4/3) è
completamente polarizzata in un piano orizzontale vale circa
(A) 53° (B) 27° (C) 45° (D) 62° (E) 33°
Soluzione Si ha polarizzazione completa dell’onda riflessa quando questa è normale a quella rifratta,
ossia quando angolo di incidenza e di rifrazione sono tra loro complementari (vedi figura). In
tal caso la legge di Snell comporta:
sinϑ
= tan ϑ = n ⇒ ϑ = tan −1 n ≈53°
cosϑ
ϑ
90°
n = 4/3
Ottica 325
Esercizio R14.10 Due polarizzatori vengono attraversati da un raggio luminoso. Quando sono orientati con assi
paralleli l’intensità luminosa emergente vale I0; quando il secondo polarizzatore viene ruotato
di ϑ = 30° rispetto al primo l’intensità luminosa emergente vale circa
(A) 0.75 I0 (B) I0 (C) 0.5I0 (D) 0.33 I0 (E) 0
Soluzione All’uscita del primo polarizzatore, il vettore campo elettrico E vibra nella direzione indicata
con n1: scomponiamo E in una componente parallela alla direzione n2 del secondo polarizzatore, di ampiezza Ecosϑ, che passerà, e in una perpendicolare, di ampiezza Esinϑ, che verrà
assorbita.
n2
n1
ϑ
E
I 0 f = ( E cosϑ ) 2 = I 0 cos2 ϑ = 0.75 I 0
Esercizio R14.11 Una palla di plastica trasparente (indice di rifrazione n = 1.42) ha un diametro esterno di 14
cm, uno interno di 10 cm ed è riempita d’aria. Un sottile pennello di luce che si propaga in
una direzione radiale proveniente da sinistra formerà una immagine a una distanza dal centro
di circa (“+” a destra, “−” a sinistra)
(A) 255 cm (B) 142 cm (C) 710 cm (D) −314 cm (E) −740 cm
Soluzione Si deve applicare la formula del diottro sferico,
nA nB nB − nA
+
=
p
q
R
successivamente alle quattro superfici aria/plastica della figura, tenendo conto dei segni e del
fatto che le distanze di oggetto e immagine, p e q, sono relative a superfici spostate le une rispetto alle altre. Per la superficie S1 si ha
1 142
.
142
. −1
142
.
+
=
⇒ q1 = 7
≈ 23.67 cm
∞ q1
7
0.42
S1
S2
−7 −5
S3
0
S4
5 7
326 Capitolo 14
L’immagine di S1 è perciò a una distanza p2 = −q1 + 2 = −21.67 cm da S2 e l’immagine di
questa superficie si forma a una distanza q2 da questa:
142
.
1
0.42
+
=−
⇒ q 2 ≈ 54.14 cm
p2
q2
5
Si ha p3 = −54.14 + 10 = −44.14 cm e
1 142
.
0.42
+
=−
⇒ q 3 ≈ −2315
. cm
p3
q3
5
Per la superficie S4 si ha p4 = 23.15 + 2 = 25.15
142
.
1 0.42
+
=
⇒ q 4 ≈ −747 cm
p4
q4
7
La distanza del fuoco dal centro è perciò 740 cm a sinistra, ovvero −740 cm.
Esercizio R14.12 La Luna è vista dalla Terra sotto un angolo ϑ ≈ 30' . Uno specchio concavo di raggio R = 1 m
focalizza una immagine della Luna di diametro
(A) 0.314 cm (B) 0.436 cm
(C) 0.5 m (D) 2 m (E) < 1mm
Soluzione Nella figura è rappresentata la geometria del problema.
ϑ
O
C
F
Il raggio di curvatura |CO| è il doppio della distanza focale |FO|. Perciò |CF| = 50 cm e la semialtezza dell’immagine si trova tracciando dai bordi della luna i raggi per C. Tale semialtezza vale
| CF| tan
ϑ
2
≈ 2.18 mm
La risposta è perciò 0.436 cm
Esercizio R14.13 Lo specchietto del dentista ha un raggio di curvatura di 24 mm. A che distanza deve trovarsi
da una carie per consentire di osservarne una immagine diritta e ingrandita di tre volte ?
(A) 12 mm (B) 16 mm (C) 4 mm (D) 10 mm (E) 8 mm
Soluzione Posto p = x, la distanza dell’immagine deve essere q = −3x e la soluzione si trova da
1 1 2
1 1
2
+ = ⇒ −
=
⇒ x = 8 mm
p q R
x 3x 24
Esercizio R14.14 A che distanza da una lente convergente di distanza focale f = 5 cm deve essere posto un
oggetto per avere una immagine virtuale ingrandita due volte?
Ottica 327
(A) 5/3 cm (B) 2.5 cm (C) 3.14 cm (D) 5 cm (E) 10 cm
Soluzione La distanza p si trova eliminando q dalle equazioni
q
− p = 2
f
1
1
=
⇒ p = = 2.5 cm
1 1 1 ⇒
2
p
f
2
+ =
q p f
Esercizio R14.15 Il sistema di lenti di un proiettore di diapositive ha una distanza focale di 20 cm mentre la
diapositiva è posta a 22 cm dal sistema di lenti. La distanza ottimale dello schermo è pari a
(A) 2 cm (B) 100 cm (C) 200 cm (D) 220 cm (E) 440 cm2
Soluzione La relazione da usare per q è
1 1
1
+ =
⇒ q = 220 cm
22 q 20
e l’ingrandimento vale dieci.
ESERCIZI PROPOSTI ___________________________________________________________
Esercizio 14.1 Nell’attraversare normalmente una lamina d’aria spessa 1 cm un raggio luminoso compie
1400 oscillazioni mentre ne compie 2300 per attraversare normalmente una lamina di vetro
spessa 1 cm. L’indice di rifrazione del vetro è pari a circa
(A) 1.23
(B) 1.31 (C) 1.64 (D) 2.31 (E) 4.13
Esercizio 14.2 Un cilindro di glicerina (nG = 1.47) di raggio R1 = 20 cm è posto al centro di un cilindro di
solfuro di carbonio (nS = 1.63) di raggio R2 = 30 cm. Quanto tempo impiega la luce di una
lampada al sodio (ν = 5.09 × 1014 Hz) per attraversare diametralmente i due cilindri? (Si assuma c = 3 × 108 m/s.)
(A) 4.13 ns (B) 2.07 ns (C) 3.14 ns (D) 3.05 ns (E) 9.80 ns
Esercizio 14.3 L’angolo di incidenza α di un raggio di luce che raggiunge la superficie di uno specchio
d’acqua (n = 4/3) per il quale raggio riflesso e raggio rifratto formano un angolo di 90° è pari
a circa
(A) 37° (B) 31.4°
(C) 48.6° (D) 53°
(E) 90°
Esercizio 14.4 L’indice di rifrazione di una lastra di ghiaccio trasparente che ricopre un laghetto vale
nghiaccio = 1.304
Dal fondo del lago (nacqua = 4/3) i raggi del sole al tramonto formano con la verticale un angolo di circa (approssimare al grado)
(A) 50°
(B)49° (C) 53° (D) 90° (E) 37°
328 Capitolo 14
Esercizio 14.5 L’indice di rifrazione del diamante è ndiamante = 2.42. Sopra quale angolo di incidenza la luce
proveniente da un diamante immerso in acqua (nacqua = 4/3) viene completamente riflessa?
(A) 33° 26' (B) 24° 24' (C) 48° 35' (D) 53° 7' (E) 37° 48'
Esercizio 14.6 Una sorgente di luce con lunghezza d’onda in aria pari a circa 589 nm (caratteristica delle
luce gialle delle lampade al sodio) illumina due fenditure parallele e su di uno schermo distante L = 0.9 m le frange luminose adiacenti sono distanti ∆y = 0.15 mm. La distanza d tra le
due fenditure vale
(A) 4.3 mm (B) 3.14 mm (C) 282 m (D) 0.098 m (E) 3.5 mm
Esercizio 14.7 La luce di una sorgente monocromatica con lunghezza d’onda λ1 = 630 nm incidente su di
una coppia di fenditure produce su di uno schermo frange luminose distanti tra loro d1 = 5
mm. Con le stesse fenditure e schermo, un altro laser produce frange distanti d2 = 4.58 mm.
La lunghezza d’onda λ2 del secondo laser vale circa
(A) 529 nm (B) 577 nm (C) 688 nm (D) 751 nm (E) indeterminato
Esercizio 14.8 Due lastre di vetro in aria con indice di rifrazione n = 1.5 appoggiano nel punto O e formano
tra di loro un piccolo angolo ϑ. Quando sono investite quasi normalmente da una luce avente
in aria una lunghezza d’onda λ = 400 nm, un osservatore posto sopra le lastre osserva frange
scure centrate nei punti O, P1, ... , P5 della figura.
C
A
ϑ
aria
h4
n = 1.5
O
P1
B
P2
P3
P4
P5
Se la distanza OP5 è pari a 0.2 cm, l’angolo ϑ tra le due lastre vale circa (in radianti)
(A) 5(10−4) (B) 7.5(10−4) (C) 3.33(10−4) (D) 3.14 (E) 1.25
Esercizio 14.9 Se l’angolo di Brewster per il quale la luce riflessa da un dielettrico opaco è completamente
polarizzata vale 62°, la costante dielettrica del materiale è di
(A) 1.88 (B) 1.47 (C) 3.54 (D) 2.13 (E) 1.13
Esercizio 14.10 Un raggio di luce non polarizzata di intensità I0 attraversa due polarizzatori che formano tra
loro un angolo di 45°. Il raggio emergente ha intensità
(A) 0.5 I0 (B) 0.375 I0 (C) 0.25 I0 (D) 0.15 I0
(E) 0.75 I0
Esercizio 14.11 Una moneta si trova sul fondo di una boccia d’acqua (n = 4/3) riempita fino a un’altezza di
Ottica 329
12 cm. Vista dall’alto, la moneta appare a una profondità dal pelo dell’acqua pari a
(A) 12 cm (B) 16 cm
(C) 9 cm (D) 6.75 cm
(E) 21.3 cm
Esercizio 14.12 Si deve formare su di uno schermo l’immagine di una lampada ingrandita di quattro volte. Si
vuole utilizzare uno specchio distante 3 m dallo schermo. Il raggio di curvatura dello specchio sarà pari a circa
(A) 1.2 m (B) 1.6 m (C) 2 m (D) 3 m (E) 12 m
Esercizio 14.13 La lunghezza focale f di uno specchio convesso che produce una immagine ridotta di un
fattore 5 di un oggetto a 8 cm dallo specchio è pari in valore assoluto a
(A) 4 cm (B) 1.6 cm (C) 2 cm (D) 1.4 cm (E) 3.3 cm
Esercizio 14.14 Una lente divergente con f = −10 cm forma l’immagine di un oggetto distante 15 cm rimpicciolita di un fattore
(A) 1 (B) 1.5 (C) 2 (D) 2.5 (E) 3.33
Esercizio 14.15 Si vuole che una diapositiva di 5 cm × 5 cm appaia sullo schermo con dimensioni 2 m × 2 m.
Se la distanza focale del proiettore è f = 25 cm, la sua distanza q dallo schermo è di circa
(A) 5 m (B) 10 m (C) 10.25 m (D) 31.4 m (E) non determinabile