Compito di Fisica Classe III B 01 dicembre ’16
Alunno
Domande:
- Come si può ricavare la legge oraria del moto uniformemente accelerato? (2. Punti)
- Cosa rappresenta l’area sottesa in grafico velocità tempo? Sapresti dare una spiegazione? (2. Punti)
Problema 1(3 Punti)
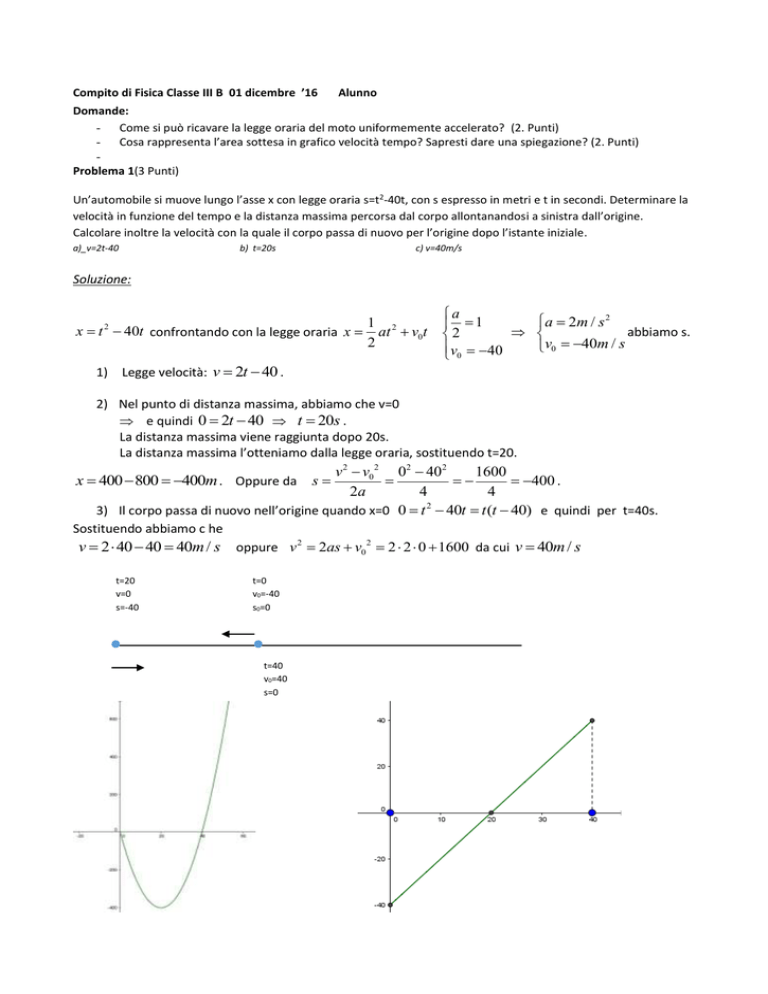
Un’automobile si muove lungo l’asse x con legge oraria s=t2-40t, con s espresso in metri e t in secondi. Determinare la
velocità in funzione del tempo e la distanza massima percorsa dal corpo allontanandosi a sinistra dall’origine.
Calcolare inoltre la velocità con la quale il corpo passa di nuovo per l’origine dopo l’istante iniziale.
a)_v=2t-40
b) t=20s
c) v=40m/s
Soluzione:
1
x t 40t confrontando con la legge oraria x at 2 v0t
2
2
a
a 2m / s 2
1
abbiamo s.
2
v0 40m / s
v0 40
1) Legge velocità: v 2t 40 .
2) Nel punto di distanza massima, abbiamo che v=0
e quindi 0 2t 40 t 20s .
La distanza massima viene raggiunta dopo 20s.
La distanza massima l’otteniamo dalla legge oraria, sostituendo t=20.
v 2 v0 2 02 402
1600
400 .
2a
4
4
3) Il corpo passa di nuovo nell’origine quando x=0 0 t 2 40t t (t 40) e quindi per t=40s.
x 400 800 400m . Oppure da s
Sostituendo abbiamo c he
v 2 40 40 40m / s oppure v 2 2as v0 2 2 2 0 1600 da cui v 40m / s
t=20
v=0
s=-40
t=0
v0=-40
s0=0
t=40
v0=40
s=0
Problema 2 (3 Punti)
Un operaio su un balcone, ad una altezza di 5 m, lancia una palla in verticale verso l’alto. Quando lascia la mano, la
palla ha velocità 11,2 m/s. a) Qual è la massima altezza raggiunta dalla palla? b) dopo quanto tempo la palla tocca il
suolo. c) calcolare lo spazio percorso dalla palla. d) Quale è la posizione della palla a t=2 s? e) A che altezza la palla ha
una velocità istantanea di 5 m/s?
a) h=11,4 m
b) t=2,67s
c) s=17,8m
d) s=7,8m
e) s=10, 1m
Soluzione:
Scrivo la legge oraria e la legge delle velocità. Considero gli assi verso l’alto quindi l’accelerazione di gravità
è negativa, e considero l’origine a terra. Da cui
1 2
s 2 gt v0t s0
Sostituendo i dati iniziali ho che
v gt v0
2 2
v v0 2 g ( s s0 )
s 4,9t 2 11, 2t 5
v 9,8t 11, 2
v 2 125, 44 19, 6( s 5)
Risposta a) la massima altezza la palla la raggiunge quando per v=0
Dalla legge delle velocità: 0 9,8t 11, 2
t
11, 2
1,143
9,8
da cui dalla legge oraria relazione hmax 4,9(1,143) 2 11, 2 1,143 5 11, 4m
oppure
ponendo v=0 alla terza relazione ho che v 2 125, 44 19,6( s 5) 125, 44 19, 6( s 5)
da cui
smax
125, 44 98
11, 4m
19, 6
b) la palla tocco il suolo nella posizione s=0 : sostituendo alla legge oraria:
0 4,9t 2 11, 2t 5 4,9t 2 11, 2t 5 0 t
11, 2 14,95
2, 67 s
9,8
b) Lo spazio totale percorso è dato dallo spazio percorso fino ad altezza massima+lo spazio per tornare alla
posizione di lancio + l’altezza del balcone
s.p. = (11,4-5)+11,4=17,8m
oppure
rappresentando il la legge della velocità calcolo l’area sottesa.
Dove per t=0 v=11,2 ,
per t=1,43 v=0
e per t=2,67 ho che v=-9.8(2,67)+11,2=-14,97
Quindi lo spazio percorso è dato dall’area dei due triangoli:
SP
11, 2 1,14 14,97 (2, 67 1,14)
6, 4 11, 4 17,8m
2
2
c) per t=2 ho che s (2) 4,9 4 11, 2 2 5 7,8
d) Dalla v 2 125, 44 19,6( s 5) sostituisco v=5 25 125, 44 19, 6( s 5)
s 10,12
Oppure ricavo t dalla legge delle velocità
5 9,8t 11, 2 da cui t 0, 63 e sostituendo
s(0,62) 4,9 (0,63)2 11, 2 0,63 5 10,11
Problema 3 (3 Punti)
Un sasso viene lasciato cadere da un ponte alto 50 m . Un altro sasso viene lanciato dallo stesso ponte, verso il basso,
un secondo dopo. Stabilire quale deve essere la sua velocità iniziale del secondo sasso affinchè tocchi l’acqua
contemporaneamente al primo.
a) v0=11,9m/s
Soluzione:
scrivo la legge oraria dei due moti:
pongo gli assi cartesiani verso il basso:
sostituendo i s=50m, le incognite sono il tempo e la velocità iniziale:
ricavo il tempo dalla prima e sostitusco alla seconda:
1 2
s1 2 gt
s 1 g (t 1) 2 v (t 1)
0
2 2
2s1
100
3, 2s
t
g
9,8
2
50 4,9(3, 2 1) v0 (3, 2 1)
2s1
100
3, 2s
t
g
9,8
v 26, 284 11,9m / s
0
2, 2
Problema 4 (3 punti)
Due atleti corrono i 100 m piani. Il primo parte con accelerazione di 4 m/s 2 e accelera per 2,5 s, dopodiché si muove di
moto rettilineo uniforme fino al traguardo. Il secondo parte con accelerazione di 2 m/s 2, accelera per 5,5 s e quindi si
muove di moto rettilineo uniforme. Quale dei due atleti giunge prima al traguardo? Qual è il distacco tra il primo e il
secondo quando il vincitore taglia il traguardo? Con quale ritardo taglia il traguardo il secondo?
a) vince il primo atleta
b) d=6,5m
c) t=0,6s
Primo atleta.
1 2
2
2
s1 at1 s1 2t1 s1 2(2,5) 12,5m
Primo tratto
2
v 4t1 v 4 2,5 10m / s
v at1
secondo tratto
s2 10(t2 2,5) 12,5
sostituendo
s2=100 100 10(t2
2,5) 12,5 87,5 10t2 25 112,5 10t2
Secondo atleta.
1 2
2
2
s1 at1 s1 1t1 s1 1(5,5) 30, 25m
Primo tratto
2
v 2t1 v 2 5,5 11m / s
v at1
secondo tratto
tempo finale
s2 11(t2 5,5) 30, 25 100 11t2 60,5 30, 25 130, 25 11t2
t2 11,84s
a) Vince il primo atleta t(primo atleta) <t(secondo atleta) .
b) Quando il primo atleta t=11,25 vince il secondo si trova nella posizione
s2 11(11, 25 5,5) 30, 25 93,5m
Quindi il distacco è
c)
Il ritardo è di
s 100 93,5 6,5m
t 11,84 11, 25 0,59s
t2 11, 25
Secondo modo
Primo atleta.
1 2
2
2
s1 at1 s1 2t1 s1 2(2,5) 12,5m
Primo tratto
2
v 4t1 v 4 2,5 10m / s
v at1
secondo tratto
tempo finale
s2 10t2
100 12,5 10t2 t2 8, 75
t t1 t2 11, 25s
t0=0
v0=0
s0=0
t1=2,5
v1=10
s1=12,5
t2=8,75
v2=10
s2=100
Secondo atleta.
1 2
s1 1t12
s1 1(5,5)2 30, 25m
s1 at1
Primo tratto
2
v 2 5,5 11m / s
v 2t1
v at1
secondo tratto:
s2 11t2 100 30, 25 11t2 t2 6,34
t1=5,5
v1=11
s1=30,25
t0=0
v0=0
s0=0
tempo finale
t2=6,34
v2=11
s2=100
t t1 t2 11,84s
a) Vince il primo atleta. Con un tempo t 11, 25s
b) Il ritardo tra i due atleti è di
inferiore al secondo atleta
t 11,84s
t 11,84 11, 25 0,59s
Infatti
c)
Quando il primo atleta vince in t=11,25 . Il secondo percorre prima 5,5 s di moto uniformemente accelerato e
poi t2=11,25-5,5=5,75 di moto rettilineo quindi
E allora in tutto in 11,25 il secondo atleta ha percorso
s2 11 5, 75 63, 25
s s1 s2 30, 25 63, 25 93,5m
E quindi la distanza tra i due atleti al momento in cui il primo taglia il traguardo è
s 100 93,5 6,5m