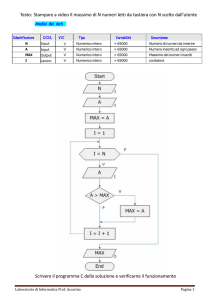
le scale di misura
DIAGNOSTICA
PSICOLOGICA
lezione
si basano su tre elementi:
sistema empirico: un insieme di entità non numeriche (es. insieme di
persone; insieme di stimoli; insieme di item)
!
Paola Magnano
[email protected]
sistema numerico: tipologia di misurazione che è possibile applicare
al sistema empirico
regola che consente il passaggio dall’uno all’altro
scala nominale
scala ordinale
sistema empirico: suddivisione in categorie distinte e
mutualmente escludentesi (es. sesso; categoria professionale)
sistema empirico: gli elementi componenti godono della stessa caratteristica
ma in quantità o in grado diverso, ordinabile rispetto a tale grado
sistema numerico: attribuire numeri uguali agli elementi della
stessa categoria e numeri diversi agli elementi appartenenti a
categorie diverse
sistema numerico: indica la posizione reciproca degli elementi; i numeri
indicano una graduatoria tra le quantità di caratteristica presenti
regola: ad uno stesso numero è associata una stessa quantità di
caratteristica
regola: i numeri sono denominazioni delle categorie
es.: spesso, raramente, mai
es.: uomini/donne
i livelli di istruzione
promosso/bocciato
i gradi di ritardo mentale
scala ad intervalli equivalenti
sistema empirico: è possibile stabilire un’unità di misura
sistema numerico: è possibile stabilire l’entità delle differenze
di intensità della caratteristica
regola: i numeri esprimono intervalli equivalenti tra le posizioni
scala a rapporti
sistema empirico: è possibile stabilire un’unità di misura e un
elemento di intensità nulla
sistema numerico: è possibile compiere tutte le operazioni e
applicare regole di trasformazione e di uguaglianza
regola: i numeri esprimono intervalli equivalenti tra le posizioni
es.: punteggi ai test
es.: misura del peso, età, lunghezza
tempi di reazione
popolazione e campione
CONCETTI
STATISTICI DI
BASE
popolazione: è l’insieme dei componenti cui l’indagine
del ricercatore è rivolta
campione: è un sottoinsieme della popolazione,
composto da un numero inferiore (n) di unità
distribuzione delle variabili
continue: possono assumere un numero
tendenzialmente infinito di valori (es. altezza,
temperatura)
discrete: possono assumere soltanto un certo
numero di valori (es. n. di risposte corrette)
distribuzione
delle
variabili
continue
!
anche se la variabile è continua, attraverso gli strumenti
di misura possiamo averne solo valori discreti (es. ansia)
distribuzione
delle
variabili
discrete
valori
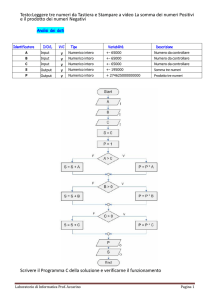
indicatori di tendenza centrale
100
90
80
moda: il valore che occorre con la maggior frequenza in
un insieme di dati di una variabile
70
60
mediana: è il valore che divide in due parti uguali la
distribuzione di frequenza di una variabile, cioè il valore al
di sopra e al di sotto del quale deve essere contenuto il
50% delle frequenza
50
40
30
20
10
0
1
2
3
4
5
6
7
media: è il valore medio di tutte le osservazioni raccolte
di una certa variabile
indicatori di dispersione
sono basati sul concetto di scostamento dalla media
varianza: è un indicatore globale di quanto i singoli
punteggi si disperdono rispetto al valore medio della
distribuzione
deviazione standard: è la radice quadrata della
varianza
distribuzione normale
un esempio
a)❩ 1, 1, 1, 2, 3, 8, 8, 8, 8
Σ=32; X= 3,55; s2x=10
b)❩ 1, 1, 2, 2, 3, 4, 5, 6, 8
Σ=32; X= 3,55; s2x=24
punti standard: i punti z
curva a campana o Gaussiana
molte variabili psicologiche presentano una
distribuzione normale o approssimativamente
normale
per rendere confrontabili tra di loro le
distribuzioni normali (che potrebbero avere media
e variabilità diversa) si trasformano in
distribuzione normale standardizzata
costituiscono la più semplice modalità di
standardizzazione dei punteggi grezzi
i punteggi grezzi si trasformano in base al punteggio
medio e alla variabilità del campione di cui il soggetto fa
parte
il punto z adatta il punteggio grezzo su una scala
standard che ha media 0 e deviazione standard 1
z = (xi - X)/s
punteggio grezzo
del soggetto
deviazione standard
del gruppo di
riferimento
media del gruppo
di riferimento
punteggio grezzo del soggetto ad un test di lettura = 25
media del gruppo di riferimento = 45
deviazione standard = 8
ALTO O
BASSO???
z = (25 - 45) / 8 = -2.5
E
M
77,56
N of Cases
144
DS
8,54
Minimum
57,000
Maximum
104,000
Median
78,000
Arithmetic Mean
77,563
Standard Deviation
8,544
Skewness
0,069
Kurtosis
0,150
Minimo
= 57
Massimo
= 104
60.48
69.02
77.56
86,1
94.64
-2
-1
0
1
2
indicatori della forma di una distribuzione
asimmetria (skewness) e curtosi (kurtosis)
variano tra più e meno infinito (±∞)
quando assumono valore = 0 indicano una forma della distribuzione normale
ci dice quanto la curva è sbilanciata
a destra o a sinistra, quindi quanto le
frequenze dei punteggi alti o bassi
sono più elevate di quanto non
dovrebbero essere se la
distribuzione fosse normale
leptocurtica
asimmetrica
ci dice quanto i punteggi siano
concentrati in un punto
particolare della distribuzione
oppure quanto essi siano
uniformi, sempre rispetto alla
distribuzione normale
normale
platicurtica
consideriamo una variabile ‘normale’ quando presenta simmetria e curtosi
comprese tra +1 e -1
IE_TOT
N of Cases
486
Minimum
58,000
Maximum
149,000
Median
112,000
Arithmetic Mean
112,119
Standard Deviation
12,214
Skewness
-0,222
Kurtosis
0,997
correlazione
si occupa della relazione tra due variabili
indica quanto l’andamento dei punteggi di
una variabile sia collegato all’andamento dei
punteggi di un’altra variabile
quindi ci dice quanto le variabili ‘co-varino’
coefficiente r di Pearson o di correlazione: si applica quando le variabili
sono misurate su scale ad intervalli e coglie relazioni di tipo lineare
regressione
spiega la relazione tra due variabili in termini
di previsione
un metodo di stima del valore atteso condizionato
di una variabile dipendente, dati i valori di altre
variabili indipendenti
misurando una variabile posso prevedere o
stimare la misura dell’altra
esempio di
relazione
non lineare