Marilena Pillati - Elementi di Statistica e di Informatica (SVIC)
«La correlazione lineare"
Analisi delle relazioni tra due caratteri
Le misure di connessione misurano il grado di
associazione tra due caratteri qualsiasi sotto il
profilo statistico (e non causale in quanto non è
compito della statistica formulare affermazioni
su rapporti di causa-effetto).
Se i due caratteri sono entrambi quantitativi,
della loro relazione si può anche, oltre che
misurare l’intensità, definire la forma.
In particolare, se il legame manifestato dai due
caratteri quantitativi X e Y è di tipo lineare, se
ne potrà misurare intensità e segno
Fonte: ISTAT, Rapporto 2007
1
Marilena Pillati - Elementi di Statistica e di Informatica (SVIC)
«La correlazione lineare"
Analisi delle relazioni tra due caratteri
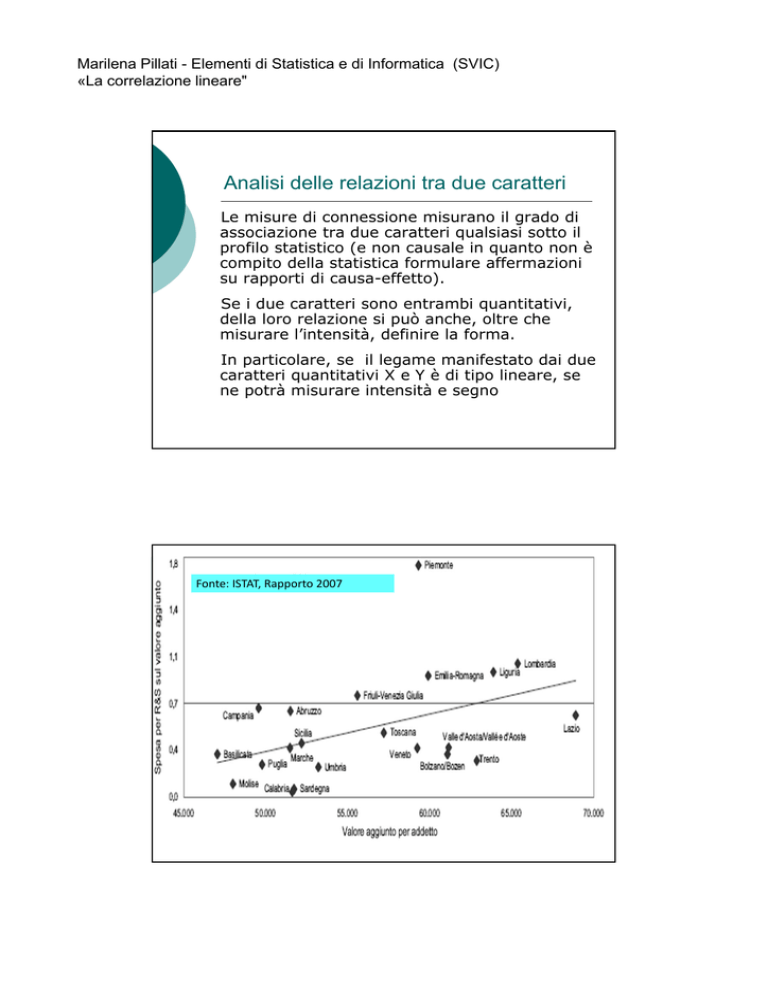
Nello scatter precedente vengono riportate le
spese per ricerca e sviluppo (Y, in ordinata) e il
valore aggiunto per addetto nelle regioni italiane
(X, in ascissa).
Emerge chiaramente un’apprezzabile relazione
diretta tra le due variabili. (Nello scatter
successivo la relazione è, invece, inversa).
a) Come misurare questa relazione?
b) Cosa significa (e come si ottiene ) la retta che
attraversa la nuvola di punti ?
Due temi da approfondire: a) la correlazione e
b) la regressione.
2
Marilena Pillati - Elementi di Statistica e di Informatica (SVIC)
«La correlazione lineare"
Analisi delle relazioni tra due caratteri
Tra due variabili X e Y esiste correlazione positiva
(concordanza) se al crescere di X anche Y, nel
complesso, tende a crescere e se al diminuire di
X anche Y, nel complesso, tende a diminuire.
La correlazione è invece negativa (discordanza)
se al diminuire di X la variabile Y, nel complesso,
tende a crescere e se al crescere di X, nel
complesso, Y tende a diminuire.
Se le variabili sono correlate, i punti dello
“scatter” si disporranno secondo un andamento
facilmente individuabile: se tale andamento è
lineare, si parlerà di correlazione lineare.
y
Y
quadrante II
quadrante I
y
x
quadrante IV
quadrante III
x
X
3
Marilena Pillati - Elementi di Statistica e di Informatica (SVIC)
«La correlazione lineare"
Classificazione delle coordinate dei punti nei 4
quadranti secondo il segno algebrico
Quadrante
Segno algebrico
yi = Yi − y
I
x i = Xi − x
+
II
-
+
III
-
-
IV
+
-
+
Codevianza e Covarianza
I prodotti ( Xi − X )( Yi − Y ) avranno segno
positivo per i punti del I e III quadrante e
negativo per i punti del II e IV quadrante.
La somma dei prodotti è detta codevianza
n
∑ ( Xi − X )(Yi − Y )
i =1
Dividendo per n si ottiene la covarianza
n
∑ ( Xi − X )(Yi − Y )
i =1
n
4
Marilena Pillati - Elementi di Statistica e di Informatica (SVIC)
«La correlazione lineare"
Codev (X,Y) > 0
prevalgono i prodotti tra scarti di segno uguale:
(+ ) ⋅ (+ )
(− ) ⋅ (− )
concordanza
Codev (X,Y) < 0
prevalgono i prodotti tra scarti di segno opposto:
(+ ) ⋅ (− )
(− ) ⋅ (+ )
discordanza
Coefficiente di correlazione lineare
Rapportando la codevianza al suo massimo si
ottiene il coefficiente r di correlazione lineare di
Bravais-Pearson:
r =
=
Codev (X ,Y )
Dev (X ) ⋅ Dev (Y )
Co var (X ,Y )
V (X ) ⋅ V (Y )
E’ un indicatore simmetrico della relazione
lineare tra Y e X
5
Marilena Pillati - Elementi di Statistica e di Informatica (SVIC)
«La correlazione lineare"
Il segno algebrico di r dipende solo dalla
covarianza e 0 ≤ r ≤ 1
r = +1
perfetta correlazione lineare positiva tra
XeY
r = -1
perfetta correlazione lineare negativa;
r=0
assenza di correlazione lineare:
caratteri linearmente indipendenti
r = +1 perfetta correlazione lineare positiva tra
X e Y; punti empirici tutti allineati su una sola
retta ascendente
6
Marilena Pillati - Elementi di Statistica e di Informatica (SVIC)
«La correlazione lineare"
r = -1 perfetta correlazione lineare negativa;
punti empirici tutti allineati su una sola retta
discendente
r = 0 assenza di correlazione lineare
Caratteri linearmente indipendenti
7
Marilena Pillati - Elementi di Statistica e di Informatica (SVIC)
«La correlazione lineare"
Il valore di r è INVARIANTE PER TRASFORMAZIONI
LINEARI operate sulle variabili originarie
Una variabile X subisce una trasformazione lineare
quando:
- viene moltiplicata per una costante b (positiva o negativa)
al valore ottenuto viene poi aggiunta un’altra costante a
(positiva o negativa)
-
La variabile Z, trasformata lineare di X, è quindi definita da:
Z = a + bX
Esempio
mese
X = prezzo del
Brent ( € barile )
Y= prezzo benzina
alla pompa ( € litro)
03/2005
40,13
1,170
06/2005
44,71
1,209
09/2005
51,32
1,303
12/2005
48,00
1,220
03/2006
51,66
1,253
06/2006
54,30
1,336
09/2006
48,48
1,269
12/2006
47,17
1,219
r = 0,914
Fonte: ENI, Bollettino Studi Energetici
8
Marilena Pillati - Elementi di Statistica e di Informatica (SVIC)
«La correlazione lineare"
Esprimiamo ora:
- il prezzo del petrolio Brent in lire per litro = Z
- il prezzo benzina in lire al netto delle accise = V
I valori da utilizzare per la trasformazione lineare sono:
-
£/€ = 1936,27
-
barile =166 litri
-
accise = 0,564€ per litro (non si considera l’IVA)
Quindi:
1
⋅ X = 11, 664 ⋅ X
166
V = 1936, 27(Y − 0,564) = −1092, 056 + 1936, 27 ⋅ Y
Z = 1936, 27 ⋅
nella 1a uguaglianza : a=0 e b=11,664
nella 2a uguaglianza : a= − 1092,056 e b=1936,27
La nuova tabella è:
mese Z = prezzo del Brent Y= prezzo benzina
( lire per litro )
alla pompa ( lire per litro
al netto accise )
03/2005
468
1173
06/2005
521
1249
09/2005
599
1431
12/2005
560
1270
03/2006
603
1334
06/2006
633
1495
09/2006
565
1365
12/2006
550
1268
r = 0,914
(invariato)
9