ESTRAZIONE DI RADICE
indice
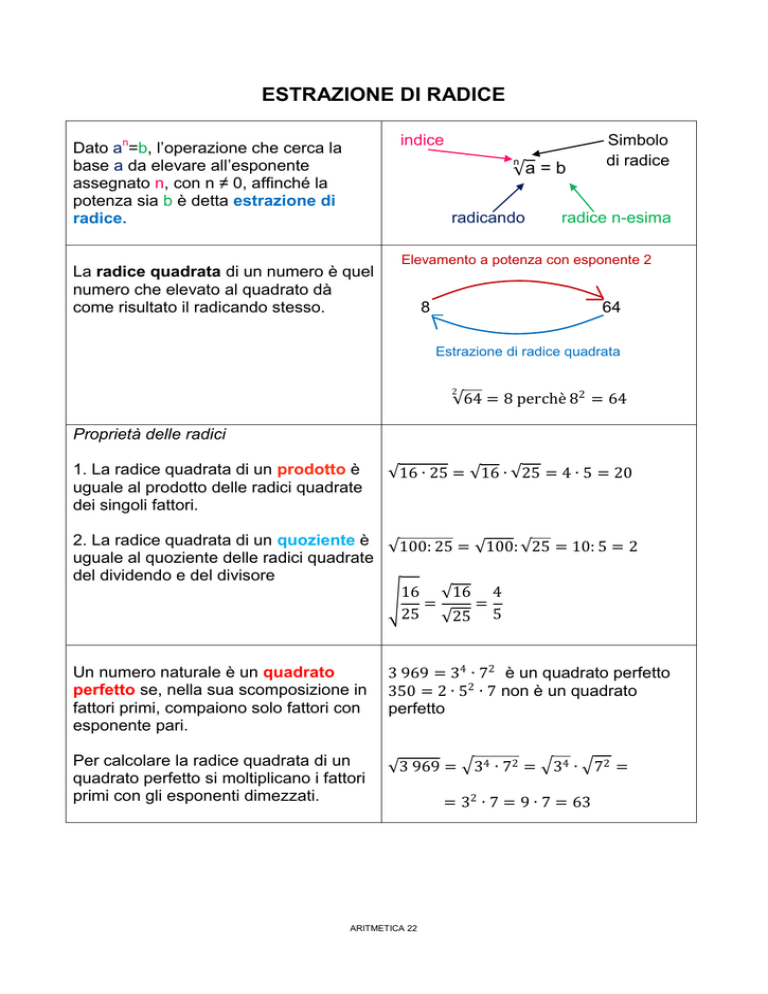
Dato an=b, l’operazione che cerca la
base a da elevare all’esponente
assegnato n, con n ≠ 0, affinché la
potenza sia b è detta estrazione di
radice.
n
a=b
radicando
La radice quadrata di un numero è quel
numero che elevato al quadrato dà
come risultato il radicando stesso.
Simbolo
di radice
radice n-esima
Elevamento a potenza con esponente 2
8
64
Estrazione di radice quadrata
2
64 = 8 perchè 82 = 64
Proprietà delle radici
1. La radice quadrata di un prodotto è
uguale al prodotto delle radici quadrate
dei singoli fattori.
16 ∙ 25 = 16 ∙ 25 = 4 ∙ 5 = 20
2. La radice quadrata di un quoziente è
uguale al quoziente delle radici quadrate
del dividendo e del divisore
100: 25 = 100: 25 = 10: 5 = 2
16
16 4
=
=
25
25 5
Un numero naturale è un quadrato
perfetto se, nella sua scomposizione in
fattori primi, compaiono solo fattori con
esponente pari.
Per calcolare la radice quadrata di un
quadrato perfetto si moltiplicano i fattori
primi con gli esponenti dimezzati.
3 969 = 34 ∙ 72 è un quadrato perfetto
350 = 2 ∙ 52 ∙ 7 non è un quadrato
perfetto
3 969 =
ARITMETICA 22
34 ∙ 72 =
34 ∙ 72 =
= 32 ∙ 7 = 9 ∙ 7 = 63
Calcolo della radice quadrata con l’uso delle tavole
Se il radicando ha un valore compreso
tra 1 e 1 000 si deve individuare il
numero nella colonna n e leggere la
radice quadrata in corrispondenza della
colonna 𝑛
676 = 26
Se il radicando ha un valore compreso
tra 1 001 e 1 000 000 si possono
presentare due casi:
Il numero si trova nella colonna 𝑛2 :
il numero è un quadrato perfetto, la
sua radice quadrata è in corrispondenza
della colonna n.
Il numero non si trova nella colonna 𝑛2 :
il numero non è un quadrato perfetto e
occorre ricorrere ad una
approssimazione.
219961 = 469
2116 < 2153 < 2209
462 < 2153 < 472
2153 =
Le radici quadrate di numeri che non
sono quadrati perfetti sono numeri
irrazionali
46 appros. per difetto
47 appros. per eccesso
Sono numeri irrazionali:
2;
3;
5;
ARITMETICA 23
6; …
R
I
Q
1
2
.
19
.
2
.
.
−
.
2
.
-2
.
.
22
.
ARITMETICA 24
.
. -13
5
.
3
.
4
3
2
5
. 9
.
-1
Z
.
N
.
-7












