René Descartes - Isaac Beeckman
Compendium Musicae
Sotto questo titolo, in Olanda, nel 1650, anno della morte di
Descartes, videro la luce alcuni suoi scritti di carattere musicale
raccolti, e forse rielaborati, da Beeckman. Quest’ultimo era un
medico, oltre che maestro della scuola di latino a Dordrecht, e
con lui Descartes aveva intrattenuto un carteggio scientifico e
filosofico. L’opera costituisce un dono personale dell’autore al
suo amico.
Descartes riprende la tradizione, millenaria, risalente a Pitagora,
sulla natura aritmetica delle armonie musicali. L’autore insiste
sull’importanza della proporzione come
origine del piacere
estetico. Ecco come, nella premessa, espone questo principio:
1° Tutti i sensi sono capaci di provare piacere.
2° È però necessario che sussista una giusta proporzione fra
l’oggetto che produce il piacere ed il senso che lo deve percepire.
Per questo il rumore di uno scoppio o di un tuono non sono adatti
a produrre musica, perché ledono l’orecchio, proprio come lede gli
occhi la luce solare troppo intensa.
3° L’oggetto deve essere tale da non presentarsi al senso in
maniera troppo difficile o confusa. Così, in un astrolabio, una
figura complessa come quella della “madre” non piacerà quanto
quella della “rete”, che è formata da linee più regolari.
4° L’oggetto che è meglio percepito dai sensi è quello nel quale
minore è la differenza tra le parti.
5° Consideriamo meno differenti tra loro le parti di un oggetto tra le
quali sussiste una maggiore proporzione.
6° Quella proporzione deve essere aritmetica, e non geometrica,
perché la prima è più apprezzabile della seconda. Ad esempio, tra
le linee:
2
3
4
la seconda delle quali è la media aritmetica delle altre due, l’occhio
avverte subito una regolarità, che invece non è in grado di
percepire tra le linee:
2
8
4
la seconda delle quali è la media geometrica delle altre due. In
effetti, le differenze tra le lunghezze delle linee nel secondo caso
sono incommensurabili, contrariamente a quanto avviene nel primo
caso.
7° Tra gli oggetti dei sensi, il più gradito allo spirito non è né
quello che viene percepito con troppa facilità, né quello che viene
percepito con troppa difficoltà: il primo non soddisfa appieno i
desideri, il secondo affatica i sensi.
8° Pertanto la varietà è sempre gradita, in ogni cosa.
Le scale musicali
Nella teoria musicale di Pitagora le frequenze delle note musicali
sono espresse da quozienti di numeri interi. Nel corso della
storia sono state inventate molte diverse scale musicali, che
presentano tutte questa caratteristica. La più nota è la scala
naturale, introdotta da Aristosseno come perfezionamento della
scala pitagorica, ed adottata anche da Tolomeo:
1/1
9/8
5/4
4/3
3/2
5/3
15/8
2/1
Do
Re
Mi
Fa
Sol
La
Si
Do+
9/4
Re+
In questa scala gli intervalli tra due note consecutive – cioè i
rapporti fra le loro frequenze - sono di tre tipi: 9/8 (tono
maggiore), 10/9 (tono minore) e 16/15 (semitono). Questa scala
musicale ha in comune con quella di Pitagora gli intervalli 1/1,
4/3, 3/2 e 2/1. Ma le restanti note vengono determinate in modo
diverso, formando medie aritmetiche:
5/4
9/8
5/3
15/8
è
è
è
è
la media aritmetica di
la media aritmetica di
la media aritmetica di
la media aritmetica di
1/1 e 3/2
5/4 e 1/1
4/3 e 2/1
3/2 e 9/4.
La scala musicale naturale viene completata con l’aggiunta di
note intermedie, per un totale di 12 note in un’ottava:
Do Reb Re Mib Mi Fa
Solb Sol
Lab La
Sib Si
In questa scala, detta cromatica dodecafonica, gli intervalli tra
due note consecutive sono sempre pari ad un semitono di valore
variabile: 25/24 (semitono minore), 27/25, 16/15 (semitono
maggiore). In effetti, gli intervalli determinati dalle note aggiunte
sono:
Reb
Mib
Solb
Lab
Sib
(Re bemolle)
(Mi bemolle)
(Sol bemolle)
(La bemolle)
(Si bemolle)
25/24
6/5
25/18
8/5
9/5
Questa scala si ottiene
inserendo una nota tra
consecutive separate da un tono:
Do
25/ 24
Reb Re Mib
16/ 15
27/25
Mi
Fa
16/ 15
25/24
Solb
27/
25/ 24
Sol Lab La
27/25
25/24
16/ 15
Sib
due note
Si
Do+
25/ 24
27/ 25
16/ 15
Il simbolo b (bemolle) indica l’abbassamento di un semitono. A
volte si usa il simbolo # (diesis) per denotare l’innalzamento di
un semitono. Così, ad esempio, si scrive Re# anziché Mib.
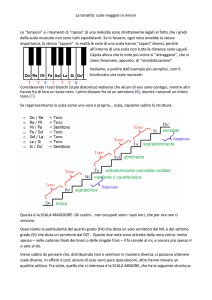
Nella scala di Do (pitagorica e naturale) gli intervalli musicali fra
due toni consecutivi sono, nell’ordine: tono, tono, semitono, tono,
tono, tono, semitono. Ora: questa successione si può costruire
anche a partire da altre note. Ad esempio, iniziando con il Fa:
Fa
Sol
La
Questa è la scala di Fa.
scale maggiori.
Sib
Do
Re
Mi
Fa+
Tutte le scale di questo tipo si dicono
Ecco come Descartes raffigura una scala musicale:
Si dice invece scala minore naturale
ogni scala in cui gli
intervalli sono: tono, semitono, tono, tono, semitono, tono, tono.
Esempio:
La
Si
Do
Re
Mi
Fa
Sol
La+
Una composizione che utilizza questa scala (tonalità) si dice in La
minore. Le tonalità precedentemente introdotte si dicono, invece,
naturalmente, Do maggiore e Fa maggiore. La scala di Do minore
è la seguente:
Do Re Mib Fa Sol Lab Sib Do+
Questa scala differisce da quella di Do maggiore solo nella terza,
sesta e settima nota. La scala minore naturale è stata poi
modificata, per motivi di eufonia. Fu inizialmente sostituita dalla
scala minore armonica, in cui la settima nota venne innalzata di
un semitono, e, successivamente, dalla scala minore melodica,
quella che oggi è maggiormente in uso, ottenuta elevando anche
la sesta nota di un semitono. In essa gli intervalli si susseguono
secondo lo schema: tono, semitono, tono, tono, tono, tono,
semitono. Le scale melodiche di La minore e Do minore sono
allora, nell’ordine:
La
Si
Do
Re
Mi
Fa#
Sol#
La+
e
Do Re Mib Fa Sol La Si Do+ .
Gli accordi
Ecco una tabella di
musicali:
Descartes contenente alcuni intervalli
Il rapporto è sempre calcolato fra la nota più bassa e quella più
alta.
Descartes concentra la propria attenzione sugli intervalli musicali
relativi a coppie di note che, suonate simultaneamente, danno
luogo ad una consonanza armoniosa. Eccoli riportati in tabella,
con le rispettive denominazioni greche (per i primi tre, quelli più
antichi, di origine pitagorica) e latine (per quelli relativi alla scala
naturale):
ottava
diapason
1:2
quinta
diapente
2:3
quarta
diatessaron
3:4
terza maggiore
ditonus
4:5
sesta minore
sesta minore
terza minore
hexachordon
minus
hexachordon
maius
semiditonus
5:8
3:5
5:6
Do – Do+
Do – Sol
Fa – Do+
Do - Fa
Sol – Do+
Do – Mi
Lab - Do+
Do – Lab
Mi – Do+
Do – La
Mib – Do+
Do - Mib
Mi - Sol
La – Do+
Questi intervalli, presi a due a due, nell’ordine, si completano ad
un’ottava. I prodotto dei loro rapporti è uguale al rapporto
dell’ottava: si tratta delle coppie diapente-diatessaron (2:3 – 3:4),
ditonus-hexachordon minus (4:5 – 5:8), hexachordon maius semiditonus (3:5 – 5:6). Descartes rappresenta queste relazioni in
figura:
Molte altre suggestive raffigurazioni si trovano in Boezio.
Vale forse la pena di spiegare l’origine dei nomi degli intervalli.
Prendiamo, per esempio, le terze: esse si chiamano così perché
sono gli intervalli tra la prima e la terza nota di una scala
musicale. La terza maggiore si riferisce ad una qualunque scala
maggiore, la terza minore ad una qualunque scala minore. Un
discorso analogo vale per le seste, e – possiamo aggiungere – per
le settime. La settima maggiore è data dal rapporto
Do : Si = 1/1 : 15/8 = 8:15
e la settima minore dal rapporto
Do : Sib = 1/1 : 9/5 = 5:9.
Esistono invece, come sappiamo, un’unica quarta ed un’unica
quinta, perché le scale maggiori e minori non differiscono nella
quarta e nella quinta nota.
Perché Descartes non include le settime nel suo elenco? La
risposta ci
viene dall’esperienza…acustica. Esse producono,
infatti, sgradevoli dissonanze (intervalli ingratissimi, come li
definisce Girolamo Saladini, matematico e teorico della musica
del 1700). Sono dissonanti anche le seconde (ad esempio: Do-Re).
Saladini, proseguendo la sua classificazione degli intervalli
musicali, considera la quarta e la quinta come consonanze meno
grate dell’ottava. Aggiunge, però, che
se il primo, il quinto e
l’ottavo tono vengono suonati simultaneamente, “si sentirà una
gratissima armonia, per cui niente resta da desiderare”. Ecco un
esempio di accordo di tre note: esso corrisponde ai rapporti
1: 3/2 : 2, cioè 2:3:4. Sono consonanti anche gli accordi basati
sui rapporti 4:5:6 nelle scale maggiori (ad esempio: Do – Mi –
Sol), e 10:12:15 nelle scale minori (ad esempio: Do – Mib – Sol).
Si tratta in ogni caso della prima, terza e quinta nota di una
scala.
Osserviamo che
nelle sequenze 2,3,4 e 4,5,6 il secondo
numero è la media aritmetica degli altri due. Ciò è vero, con
buona approssimazione, anche per 10,12,15, il che conferma
l’importanza della media aritmetica nell’armonia musicale,
dando ragione a Descartes. Esiste, però anche una scala musicale
basata sulla media geometrica: si tratta della scala
temperata, in cui ogni ottava è suddivisa in dodici semitoni del
valore pari alla radice dodicesima di 2.
Ogni intervallo musicale può essere rappresentato indifferentemente da un quoziente o dal suo reciproco: la quarta
corrisponde a 3/2 o a 2/3, a seconda che si voglia mettere a
numeratore la nota più alta o quella più bassa. Per questo
motivo, accanto alla media aritmetica si considera spesso la
media armonica di due intervalli musicali, che è il reciproco
della media aritmetica dei reciproci dei medesimi intervalli. Il
nome stesso sottolinea il ruolo fondamentale svolto nella
determinazione delle consonanze musicali.
Ecco perché il
Saladini, nel suo Nuovo metodo delle proporzioni geometrica,
aritmetica ed armonica, così presenta la sua opera: “per far
intendere in qualche parte come la proporzione Armonica
s’ingerisca nella Musica, e quanto sia necessario lo studio della
Geometria, e dell’Aritmetica a coloro che si danno ad una tal
facoltà.”