Ottica
LEYBOLD Schede di fisica
Ottica ondulatoria
Anelli di Newton
LEYBOLD
Schede di fisica
P5.3.3.1
P5.3.3.1
Anelli di Newton con fascio
di luce monocromatica
Obiettivi dell’esperimento
n Dimostrare come si ottengono gli anelli di Newton per interferenza di un fascio di luce monocromatica che attraversa
una lamina di vetro ed una lente pianoconvessa.
n Determinare il raggio di curvatura della lente pianoconvessa attraverso la misura degli anelli di Newton ottenuti mediante
la luce gialla di una lampada al sodio.
n Analizzare la relazione che intercorre tra gli anelli di Newton e la lunghezza d’onda della luce quando si utilizza il raggio
monocromatico di una lampada al mercurio.
Principio fisico
0106-Kem/Sel
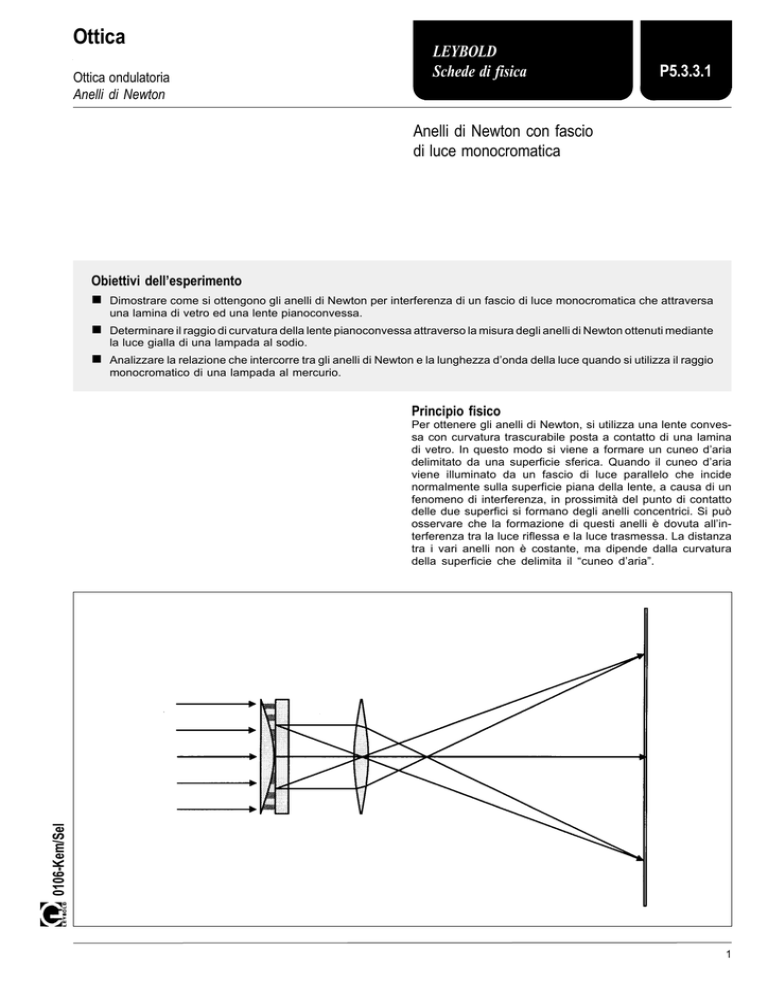
Per ottenere gli anelli di Newton, si utilizza una lente convessa con curvatura trascurabile posta a contatto di una lamina
di vetro. In questo modo si viene a formare un cuneo d’aria
delimitato da una superficie sferica. Quando il cuneo d’aria
viene illuminato da un fascio di luce parallelo che incide
normalmente sulla superficie piana della lente, a causa di un
fenomeno di interferenza, in prossimità del punto di contatto
delle due superfici si formano degli anelli concentrici. Si può
osservare che la formazione di questi anelli è dovuta all’interferenza tra la luce riflessa e la luce trasmessa. La distanza
tra i vari anelli non è costante, ma dipende dalla curvatura
della superficie che delimita il “cuneo d’aria”.
1
P5.3.3.1
LEYBOLD Schede di fisica
Apparecchiature
1
2
1
1
1
6
1
1
1
1
1
1
1
1
1
Lamina di vetro per gli anelli di Newton
Lenti con montatura, f = +100 mm
Diaframma ad iride con montatura
Sostegno con morsetti a molla
Banco ottico a profilo normalizzato
Cavalieri ottici, altezza: 60 mm,
larghezza: 36 mm
Lampada a vapori di Na
Lampada a vapori di Hg
Sostegno per lampade a luce monocromatica
Reattanza universale
Filtro per lo spettro dei vapori di Hg, giallo
Filtro per lo spettro dei vapori di Hg, verde
Filtro per lo spettro dei vapori di Hg, blu
Schermo semitrasparente
Zoccolo
471
460
460
460
460
11
03
26
22
32
460
451
451
451
451
468
468
468
441
300
353
111
062
16
30
30
31
32
53
11
Fig.1: Rappresentazione schematica dell’interferenza nel cuneo d’aria
In Fig.1, un’onda luminosa L proveniente da sinistra colpisce
un cuneo d’aria di spessore d compreso tra due piani di
vetro. Parte dell’onda, indicata con T1, viene riflessa dalla
superficie di sinistra che separa il piano di vetro dal cuneo
d’aria. Parte dell’onda, indicata con T2, attraversa il cuneo
d’aria. L’onda T3, riflessa dalla superficie di separazione di
destra, subisce una inversione di fase dovuta all’elevato indice di rifrazione del mezzo. L’onda T4 viene prima riflessa
dalla superficie di separazione di destra e successivamente
dalla superficie di separazione di sinistra; in corrispondenza
di ogni riflessione, l’onda subisce una inversione di fase. Le
ulteriori onde parziali con le corrispondenti rotazioni di fase
dovute alle riflessioni multiple all’interno del cuneo d’aria,
sono rappresentate con T5. È possibile, ora, analizzare l’interferenza tra le onde riflesse T1 e T3, l’interferenza tra le
onde T2 e T4 e l’interferenza tra tutte le altre onde dovute alla
luce trasmessa.
La differenza di percorso ∆ tra le onde T2 e T4 è data da:
λ
(I)
2
Per avere interferenza, è necessario che sia soddisfatta la
condizione
∆ = 2d + 2 ⋅
∆ = n ⋅ λ con n = 1, 2, 3 ...
questo si verifica quando:
λ
con n = 1, 2, 3 ...
(II)
2
Se le due superfici di vetro si toccano, cioè se d = 0, i
fenomeni di interferenza si verificano sempre nella direzione
di propagazione, indipendentemente dalla lunghezza d’onda
della luce incidente. Per effetto della riflessione si ha sempre
la sparizione del raggio luminoso, in quanto T3 subisce un’inversione di fase. Ad una distanza di valore finito, l’interferenza dipende dallo spessore d del cuneo d’aria e dalla lunghezza d’onda λ del raggio luminoso. Nel caso in cui la luce viene
trasmessa attraverso un cuneo d’aria delimitato da una lente
convessa, si ha la seguente situazione.
Lo spessore d dipende dalla distanza r dal punto di contatto
della lente convessa con la superficie di vetro e dal raggio di
curvatura R della lente convessa. Dalla Fig. 2 si ottiene la
seguente relazione
d = ( n − 1) ⋅
R2 = r2 + (r – d)2
2
dalla quale si ricava:
d=
r2
2R
(III)
valida per piccoli valori dello spessore d. Gli anelli dovuti
all’interferenza, cioè gli anelli luminosi, si possono calcolare
mediante la relazione:
rn2 = ( n − 1) ⋅ R ⋅ λ con n = 1, 2, 3 ...
(IV)
Se si esercita una leggera pressione sulla lente piano convessa in corrispondenza del punto di contatto e si vuole tener
conto di tale azione, bisogna modificare l’equazione (III). Per
ottenere una migliore approssimazione bisogna apportare la
seguente modifica:
d=
r2
− d0 con r ≥ 2 Rd 0
2R
(V)
Per calcolare i raggi rn degli anelli luminosi dovuti all’interferenza, si utilizza la seguente relazione:
rn2 = ( n − 1) R λ + 2 R d0 con n = 1, 2, 3 ...
(VI)
Fig. 2: Rappresentazione schematica del cuneo d’aria compreso tra la
superficie di vetro e la lente pianoconvessa
P5.3.3.1
LEYBOLD Schede di fisica
Fig.3: Montaggio dell’esperimento su banco ottico e posizioni dei cavalieri ottici riferite alla terminazione di sinistra
(a)
Lampada a vapori di Na (o Hg)
(d)
Lamina di vetro per gli anelli di Newton
(b)
Sostegno con morsetti a molla
(e)
Lente, f = 100 mm
(c)
Lente, f = 100 mm
(f)
Diaframma ad iride
Configurazione del sistema di misura
Nota: Quando si eseguono le misure è necessario che la
stanza sia il più possibile al buio.
Lamina di vetro per gli anelli di Newton
– Disporre le “lamine per gli anelli di Newton” di fronte ad
uno sfondo illuminato ed osservarle attraverso la luce riflessa. Inizialmente, svitare completamente le viti zigrinate.
– Stringere con cura le viti zigrinate in modo da
a) portare in contatto le superfici di vetro (cioè in modo
che dal centro non si formino ulteriori anelli di interferenza e l’anello di interferenza più interno sia scuro);
b) ottenere un insieme di anelli perfettamente al centro
della scala di lettura (gli anelli si muovono continuamente
quando si stringe la vite zigrinata).
Nota: Un aumento della pressione nel punto di contatto potrebbe deformare le due superfici
Montaggio del banco ottico
La Fig.3 mostra lo schema di montaggio dell’esperimento.
– Montare i vari componenti sul banco ottico; rispettare le
posizioni dei cavalieri ottici specificate precedentemente.
– Posizionare lo schermo semitrasparente ad una distanza
compresa tra 1 m e 2 m.
– Predisporre il sostegno delle “lamine per gli anelli di
Newton” (d) in modo tale da regolare con le viti l’esposizione sullo schermo semitrasparente. Far scorrere il cavaliere ottico il più vicino possibile alla lente (c).
– Inserire la lampada a vapori di Na. Collegare la reattanza
universale e chiudere l’interruttore. Dopo una fase di riscaldamento di qualche minuto, spostare il cavaliere ottico fino ad illuminare in modo ottimale le “lamine per gli
anelli di Newton”.
– Variare la posizione della lente (e) o lo schermo
semitrasparente fino ad ottenere la formazione degli anelli di Newton e facendo in modo che la scala sia leggibile
senza difficoltà.
– Se è necessario controllare e regolare nuovamente la
posizione delle “lamine per gli anelli di Newton”, usare la
vite zigrinata (l’anello più interno si deve illuminare!).
Esecuzione dell’esperimento
Nota: Una volta eseguita la regolazione delle lamine per gli
anelli di Newton, non modificare più la configurazione del
sistema di misura. In particolare, evitare di toccare le viti di
regolazione.
a) Misura con la lampada a vapori di Na
– Ottimizzare il contrasto chiaro-scuro degli anelli di Newton
mediante il diaframma ad iride (f).
– Tramite la scala graduata, misurare e prendere nota dei
punti di intersezione rL sul lato sinistro e dei punti di
intersezione rR sul lato destro.
b) Misura con la lampada a vapori di Hg
Attenzione:
Prima di rimuovere le lampade a luce monocromatica bisogna
lasciarle raffreddare oppure prenderle dopo averle avvolte
con un panno.
–
–
–
–
–
–
Sostituire la lampada a vapori di Na con quella a vapori
di Hg.
Chiudere l’interruttore della reattanza universale ed attendere qualche minuto per la fase di riscaldamento.
Osservare le frange colorate degli anelli di Newton.
Bloccare il filtro giallo nell’apposito sostegno. Ottimizzare
il contrasto chiaro-scuro degli anelli di Newton mediante
il diaframma ad iride (f).
Tramite la scala graduata, misurare e prendere nota dei
punti di intersezione rL sul lato sinistro e dei punti di
intersezione rR sul lato destro.
Ripetere la misura con i filtri di colore giallo, verde e blu.
3
P5.3.3.1
LEYBOLD Schede di fisica
Esempio di misura
Tabella 1: Intersezioni degli anelli di Newton a destra ed a
sinistra della scala con lampada a vapori di Na
Fig.4: Relazione tra i raggi r dei cerchi di interferenza luminosi ed il
numero d’ordine n con sorgente luminosa sulla riga D dello
spettro del Na
Tabella 2: Intersezioni degli anelli di Newton a destra ed a
sinistra della scala con lampada a vapori di Hg e luce di
colore giallo, verde, blu.
Giallo
Verde
b) Misura con la lampada a vapori di Hg
La Fig. 5 fornisce il legame tra rn2 ed n per raggi luminosi
appartenenti alle righe dello spettro della lampada a vapori
di Hg. In base all’equazione (VI) (vedere Tabella 3), la pendenza delle rette aumenta proporzionalmente con la lunghezza d’onda delle righe dello spettro del Hg.
Blu
Fig. 5: Relazione tra i raggi r dei cerchi di interferenza luminosi ed il
numero d’ordine n con sorgente luminosa gialla (triangoli), verde
(quadrati) e blu (cerchi) dello spettro del Hg.
Valutazione
a) Misura con la lampada a vapori di Na
I risultati della misura contenuti nella Tabella 1 sono riportati
nel diagramma di Fig. 4. I valori del raggio r sono stati
ottenuti facendo la media tra rL ed rR.
La pendenza della retta che unisce i vari punti vale:
∆r 2
= 10.7 mm2
∆ ( n − 1)
Mediante l’equazione (VI) e la lunghezza d’onda λ = 589 della
riga D dello spettro del Na, si può calcolare il raggio di curvatura della lente convessa il cui valore risulta: R = 18.3 m
La sezione perpendicolare all’asse
r 2 ( n = 1) = 5.0 mm2
si riferisce ad una superficie piana distante dal punto di
contatto della lente della quantità:
d0 = 0.14 µm
4
Tabella 3: Pendenza delle rette di Fig. 5
Colore
Blu
Verde
Giallo
Risultati
La struttura concentrica e la variazione dei raggi dei cerchi
di Newton si può spiegare tenendo conto della curvatura
sferica della lente convessa che delimita il cuneo d’aria.
Quando il cuneo d’aria viene illuminato con luce bianca, gli
anelli di interferenza sono circondati da frange colorate poiché il loro diametro aumenta con la lunghezza d’onda (vedere (IV) e (VI)).
LEYBOLD S.p.A. Divisione Didattica - Via Trasimeno, 8 - 20128 Milano - Resp. di Divisione: (02) 27223215 - Ufficio Commerciale: (02) 27223216
Servizio Tecnico: (02) 27223207 - Fax: (02) 27203037 - E-mail: [email protected] - http://www.leybold.it









