forze fondamentali e unificazione

FORZE FONDAMENTALI E UNIFICAZIONE *
SOMMARIO
1. Gli inizi: gravità terrestre e celeste
2. Elettromagnetismo classico
3. Meccanica Quantistica: atomi e nuclei
4. Modello Standard: particelle elementari e loro interazioni elettro-deboli e forti
5. Relatività Generale: problemi con la Meccanica Quantistica, stringhe e M-teoria
6. Cosmologia, inflazione e CMB
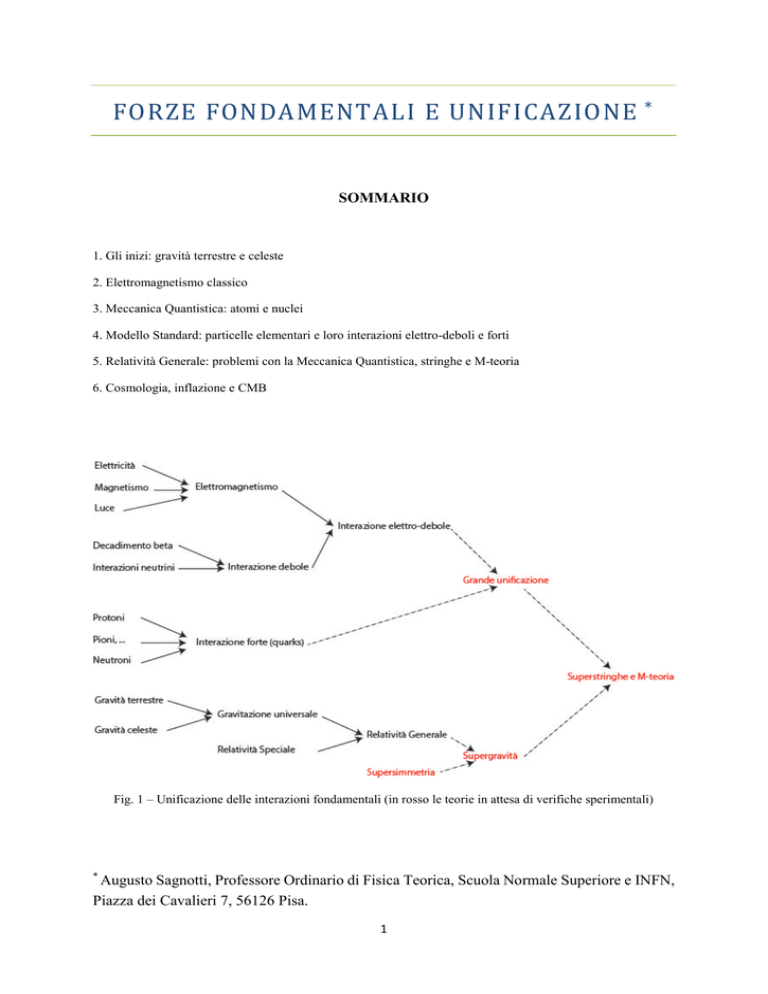
Fig. 1 – Unificazione delle interazioni fondamentali (in rosso le teorie in attesa di verifiche sperimentali)
*
Augusto Sagnotti, Professore Ordinario di Fisica Teorica, Scuola Normale Superiore e INFN,
Piazza dei Cavalieri 7, 56126 Pisa.
1
1. Gli inizi: gravità terrestre e celeste
Gli inizi della Fisica moderna vengono comunemente associati ai contributi di Galileo Galilei.
In questa discussione, dedicata all’emergenza del concetto di forza fondamentale,
all’identificazione di gravità, elettromagnetismo e altre forze e allo stato attuale del progetto di
una loro unificazione (Fig. 1), basterà ricordare brevemente il suo contributo alla definizione
del metodo di ricerca scientifica. Si tratta di una sapiente alternanza di esperimenti e tentativi
di inquadrarli in leggi matematiche, teorie appunto, per estrarne nuove predizioni da sottoporre
al vaglio di nuovi esperimenti, che ha regolato per quattro secoli lo sviluppo della Fisica.
Questo procedimento richiedeva, e richiede tuttora, l’identificazione di contesti semplificati in
cui i sistemi oggetto di indagine siano dominati da pochi gradi di libertà. Nella storia che ci
accingiamo a narrare questa strada porta naturalmente dai corpi macroscopici ad atomi, nuclei
e particelle elementari, e in questo contesto si può ben parlare di riduzionismo. Ma mi preme
sottolineare che la riduzione a pochi gradi di libertà accompagna la comprensione di ogni
fenomeno fisico, anche perché aiuta la mente umana a visualizzarlo e consente alla Matematica
di darne conto in modo non eccessivamente complicato. La stessa problematica si ripresenta in
sistemi con grandissimi numeri di particelle, per i quali la Termodinamica coinvolge infatti
pochi concetti globali come temperatura, pressione e volume.
Nello studio dei gravi su piani inclinati, l’accurata levigazione degli stessi consentì a
Galilei di evidenziare il moto uniformemente accelerato, grazie all’ulteriore accortezza di
servirsi di corpi piccoli, quelli che si possono ben schematizzare come punti materiali. Ad
esempio, la salita di una carriola su una tavola inclinata è favorita dalla riduzione dell’effettiva
forza di gravità, parte della quale viene appunto assorbita dalla tavola, ma l’essenza del
fenomeno si può ben comprendere schematizzando la carriola con un singolo punto materiale.
Isaac Newton, come è noto, fece tesoro dei risultati di Galilei. La sua famosa equazione
dinamica
𝑚𝑚 𝒂𝒂 = 𝑭𝑭
dà conto, in linea di principio, di tutta la dinamica macroscopica in un contesto deterministico.
Qui m è la massa della particella e la forza F è tutto quanto dà luogo ad accelerazione. Questo
è vero in particolare per la forza di gravità nei pressi della superficie terrestre. In questo caso
𝑭𝑭 = 𝑚𝑚 𝒈𝒈, e quindi punti materiali di diverse masse hanno la stessa accelerazione. Questa forma
di universalità è una manifestazione del “principio di equivalenza” e, come vedremo, avrà un
ruolo chiave nella Relatività Generale.
La legge di Newton contiene una prima realizzazione di un legame molto profondo tra
simmetrie continue e leggi di conservazione di opportune “cariche” che fu compreso appieno,
nei primi anni del Novecento, dalla matematica tedesca Emmy Noether. La qualifica è molto
importante: una trasformazione di simmetria può essere in generale discreta o continua, e le
leggi di conservazione emergono solo nel secondo caso. Esempi di trasformazioni discrete sono
2
la parità, corrispondente all’inversione di tutte le coordinate spaziali, e l’inversione temporale,
mentre le rotazioni nello spazio sono un classico esempio di trasformazioni continue. In un
sistema fisico invariante sotto rotazioni si conserva il momento angolare totale, mentre ad
esempio in un sistema invariante per traslazioni temporali si conserva l’energia.
Newton procedette ben oltre, proponendo una legge per l’attrazione gravitazionale tra
due punti materiali: una forza diretta lungo la loro congiungente e d’intensità
𝐹𝐹 =
𝐺𝐺 𝑚𝑚1 𝑚𝑚2
𝑟𝑟 2
Questa semplice legge di forza è regolata dalla costante universale G, è proporzionale al
prodotto delle masse ed è inversamente proporzionale al quadrato della loro distanza. Newton
derivò da questa espressione le leggi di Keplero dei moti planetari, nei quali sole e pianeti sono
ben schematizzati come punti materiali. Inoltre, riuscì a collegare g, l’intensità
dell’accelerazione di gravità sulla superficie terrestre, alla costante G, alla massa 𝑀𝑀𝑇𝑇 della terra
e al suo raggio 𝑅𝑅𝑇𝑇 . La relazione risultante,
𝑔𝑔 =
𝐺𝐺 𝑀𝑀𝑇𝑇
2
𝑅𝑅𝑇𝑇
riconduce la gravità terrestre a quella celeste, e può ben dare un’idea di ciò che i fisici intendono
per unificazione. Di conseguenza, la sola gravitazione universale resta di diritto nel catalogo
delle interazioni fondamentali.
2. Elettromagnetismo classico
Nel XIX secolo fece la sua piena comparsa, in un gran numero di ricerche, il secondo
tipo di interazione presente in Natura che si manifesta a scale macroscopiche. Questo avviene
in fenomeni apparentemente complicati e diversi, che comprendono l’elettrizzazione per
strofinio, il comportamento di circuiti elettrici in corrente continua, i magneti permanenti, le
interazioni magnetiche tra correnti, e anche l’induzione elettromagnetica che è alla base dei
motori elettrici. Il primo risultato di rilievo, in questo senso, fu l’identificazione della forza di
Coulomb tra due cariche elettriche puntiformi in quiete, la cui intensità
𝐹𝐹 =
𝑄𝑄1 𝑄𝑄2
𝑟𝑟 2
rivela chiaramente una suggestiva analogia con la formula di Newton che abbiamo appena
descritto. Vedremo a breve che questo riflette proprietà profonde e interessanti.
I fondamentali esperimenti del fisico inglese Michael Faraday e altri sono riassunti in
un insieme di equazioni di rara eleganza, note come equazioni di Maxwell:
∇. 𝑬𝑬 = 4 π ρ , ∇. 𝑩𝑩 = 0, ∇ x 𝑬𝑬 = −
3
1 ∂ 𝑩𝑩
4π
1 ∂ 𝑬𝑬
, ∇ x 𝑩𝑩 =
𝑱𝑱 +
𝑐𝑐 ∂ 𝑡𝑡
𝑐𝑐
𝑐𝑐 ∂ 𝑡𝑡
Mi limiterò qui ad osservare che le quantità coinvolte, oltre alla velocità della luce c, sono il
campo elettrico E, il campo magnetico B, la densità di carica elettrica ρ e la densità di corrente
elettrica J. Alla loro base troviamo il concetto nuovo e sottile, ma molto importante, di campo.
I campi elettrici e magnetici sono generati da cariche e correnti, e a loro volta determinano le
forze su altre cariche tanto tenui da non disturbarle. Il punto sul quale vorrei richiamare
l’attenzione è l’ultimo termine presente nell’ultima equazione. Il fisico scozzese James Clerk
Maxwell lo introdusse per pure ragioni di consistenza matematica, e i suoi effetti sono sotto i
nostri occhi. L’aggiunta di questo termine porta infatti alla propagazione per onde nello spazio
vuoto, alla velocità della luce c, di tutti i fenomeni elettromagnetici. Questi includono anche la
luce visibile in una piccola porzione dello spettro di lunghezze d’onda, e pertanto si può ben
dire che la luce del sole raggiunge la terra proprio grazie al termine aggiuntivo!
3. Meccanica Quantistica: atomi e nuclei
La teoria di Newton, e ancor più l’eleganza delle equazioni di Maxwell, diedero ai nostri
antenati di fine Ottocento l’illusione che tutti i fenomeni fisici fossero ormai compresi. I
tentativi di applicare queste leggi al mondo microscopico causarono però un brutto risveglio.
Il primo problema che appariva insolubile aveva a che fare, al netto delle schematizzazioni,
con il colore dei corpi caldi. Se mettiamo un tronco di legna sul fuoco, sappiamo bene che
quando inizia ad ardere diventa rossastro e poi tende al biancastro. Nel passare dal rossastro al
biancastro la lunghezza d’onda dominante della luce emessa deve quindi diminuire, in
corrispondenza con l’aumento della temperatura. Il fisico tedesco Max Planck riuscì nel 1900
a dar conto di questo fenomeno, a fronte del quale la Fisica Classica, ovvero la combinazione
delle teorie di Newton e Maxwell con la Termodinamica, impazziva, ma al prezzo di introdurre
un’altra costante fondamentale, h. Questa costante, detta conseguentemente “costante di
Planck”, non segnala una nuova forza, ma nuove leggi della dinamica che solo nel mondo
macroscopico si riducono alla legge di Newton. La nuova dinamica è detta Meccanica
Quantistica, e portarla alla sua forma attuale ha richiesto l’intera prima metà del secolo scorso
e brillanti contributi di moltissimi scienziati.
Le novità concettuali più importanti della Meccanica Quantistica discendono da
un’analisi critica dei processi di misura nel mondo microscopico. Questa implica ad esempio
il famoso principio di indeterminazione di Heisenberg,
∆𝑥𝑥 ∆𝑝𝑝 ≥
ℎ
4π
che fissa un limite inferiore per la precisione di misure simultanee di posizione e quantità di
moto per una particella, soppiantando l’idea classica di punto materiale. In tal modo le
particelle acquistano attributi delle onde, e viceversa le onde elettromagnetiche acquistano
attributi delle particelle. Solo le probabilità di possibili eventi, e non più le traiettorie, restano
oggetto di predizione, insieme a caratteristiche generali come i possibili spettri delle energie
disponibili. La costante h ha conseguenze drammatiche sulla nostra comprensione della Natura:
4
come notò ben presto il fisico danese Niels Bohr, essa implica la stabilità degli atomi e la natura
discreta degli spettri di emissione e assorbimento dei gas, in accordo con una serie di
sorprendenti osservazioni di fine Ottocento. Tradotto in termini meno tecnici, un gas può
emettere luce, ma questa porta il suo sigillo, nel senso che se la luce viene analizzata con
opportuni strumenti essa rivela la presenza di speciali lunghezze d’onda o linee spettrali.
Fig. 2 – Tavola periodica degli elementi
Con l’aggiunta del principio di esclusione formulato dal fisico tedesco Wolfgang Pauli,
che introduce una sorta di effettiva repulsione a corto raggio tra elettroni e altri fermioni se
identici, la Meccanica Quantistica fornisce un’elegante giustificazione concettuale della tavola
periodica (Fig. 2). Gli atomi contengono nella loro zona centrale dei nuclei, tanto piccoli
rispetto al tutt’uno quanto una pallina da tennis rispetto ad un campo di calcio. I nuclei sono
carichi positivamente, in quanto contengono un certo numero di particelle pesanti di carica
positiva, dette protoni, oltre ad alcune particelle neutre dette neutroni. Mi limiterò qui a dire,
al costo di essere impreciso, che gli elettroni che compensano la carica dei protoni riempiono
orbitali disponibili intorno al nucleo, iniziando da quello di energia inferiore, in accordo con il
“principio di Pauli”. La struttura degli orbitali occupati più esterni determina le proprietà
chimiche degli elementi.
Una nuova formulazione della Meccanica Quantistica, equivalente ma molto
suggestiva, è emersa negli anni Quaranta del secolo scorso grazie al fisico americano Richard
Feynman. Essa associa ad una particella tutti i possibili cammini, e ad ognuno di essi un numero
complesso a+ib, dove a e b sono due numeri reali e i è l’unità immaginaria. Le probabilità della
Meccanica Quantistica emergono in tal modo da una somma su questi cammini, che includono
la traiettoria classica della teoria di Newton.
Le speranze di giungere, nello studio dei nuclei, ad un livello di comprensione simile a
quello ottenuto per gli atomi si rivelarono ben presto poco realistiche. Anzitutto, questi sistemi
coinvolgono interazioni molto intense tra molte particelle, mentre negli atomi dominano quelle
tra il nucleo e i singoli elettroni. Di conseguenza, le forze che tengono insieme i nuclei appaiono
estremamente complicate. Inoltre i due tipi di particelle presenti, protoni e neutroni, si sono
rivelati dei composti di altre particelle elementari dette quarks. Protoni e neutroni interagiscono
tra loro, fortemente e in numeri consistenti, nei nuclei, e sono tenuti insieme da un nuovo tipo
di forza. La nuova forza è detta interazione forte, è circa cento volte più intensa delle forze
5
elettrostatiche ma si manifesta solo a distanze confrontabili con le dimensioni dei nuclei, che
tiene insieme contrastando la repulsione elettrostatica tra i protoni. Quando i protoni diventano
un centinaio o poco più, infatti, la repulsione elettrostatica prevale, i nuclei stabili cessano di
esistere e la tavola di Medeleev termina. Esistono inoltre trasformazioni dei nuclei, poco
frequenti, che coinvolgono l’emissione di nuove particelle leggere ed elusive, dette neutrini, la
cui esistenza fu ipotizzata da Pauli. Questo fenomeno venne associato da Enrico Fermi ad una
nuova forza fondamentale molto meno intensa, detta appunto interazione debole (Fig. 3).
Fig. 3 – Un protone (p) si trasforma in un neutrone (n), un positrone (e+) e un neutrino (ν).
4. Modello Standard: particelle elementari e loro interazioni elettro-deboli e forti
Galilei identificò un primo principio fondamentale della dinamica, i cui effetti sono
giornalmente sotto i nostri occhi: nulla distingue due sistemi di riferimento “inerziali” in moto
relativo rettilineo e uniforme. Grazie a questo principio, ad esempio, riusciamo a spostarci
agevolmente su aerei che viaggiano a quasi 1000 Km/h, senza avvertirne il movimento in tratti
privi di turbolenza! Le equazioni di Maxwell sembrano violarlo, a meno che le regole di
trasformazione tra due sistemi inerziali non siano profondamente alterate nel caso di velocità
prossime a quella della luce. Ad esempio, se avanziamo a velocità ordinarie lungo un treno con
velocità v e il treno avanza con velocità V, un osservatore a terra ci vede procedere con velocità
v+V. Ebbene, mettendo a frutto una serie di contributi precedenti, Einstein si rese conto che la
formula corretta è in realtà
𝑣𝑣 + 𝑉𝑉
𝑣𝑣 𝑉𝑉
1+ 2
𝑐𝑐
Questa espressione si riduce al risultato precedente per velocità molto minori di c (che è circa
un miliardo di Km/h!), ma è semplice verificare che, se noi (o il treno) ci muovessimo alla
velocità della luce, o in altri termini se v o V fosse uguale a c, il risultato sarebbe
sorprendentemente ancora c. La velocità della luce costituisce pertanto una barriera
impenetrabile, e può essere raggiunta solo da particelle di massa nulla. Un’altra conseguenza
di questa analisi è la famosa relazione che lega la massa e l’energia di riposo di una particella
𝐸𝐸0 = 𝑚𝑚 𝑐𝑐 2
e viene spesso associata, in modo inquietante, alle esplosioni nucleari. Queste e altre modifiche
racchiuse nella Relatività Speciale rendono le equazioni di Maxwell perfettamente compatibili
con il principio di Galilei, e mescolando spazio e tempo tra loro nel collegare diversi sistemi di
6
riferimento in un certo senso li unificano nello spazio-tempo. Esse predicono anche una serie
di altri fenomeni apparentemente esotici che sono stati verificati con altissima precisione.
La Meccanica Quantistica porta ad una riproposizione, in un contesto onda-particella,
dei punti materiali, che in questa nuova incarnazione prendono il nome di quanti. Il quanto di
luce è detto fotone, e i fotoni sono identici tra loro (come tutte le altre particelle di uno stesso
tipo) a parte pochi attributi dinamici. Inoltre, essi sono bosoni, e come tali nulla osta che si
addensino, e sorgenti luminose macroscopiche ce ne inviano numeri talmente elevati che la
natura granulare del fenomeno emerse solo nei primi anni del secolo scorso. I fotoni sono
particelle di massa nulla, e questo implica sia la legge di Coulomb che la propagazione delle
onde elettromagnetiche alla velocità c. Le interazioni forti e deboli sono invece a corto raggio
d’azione a causa di diverse proprietà del vuoto. I loro effetti, limitati a distanze dell’ordine
delle dimensioni dei nuclei o anche molto inferiori, sono responsabili del fatto che una loro
chiara identificazione risale solo agli anni Settanta del secolo scorso. Le forze forti sono in
realtà più intense e complesse, e danno luogo ad un complicato zoo di particelle composte
instabili che si disintegrano rapidamente. I loro effetti si avvertono solo a brevissime distanze
a causa di un sottile effetto, detto confinamento, che rende impossibile produrre
individualmente le particelle elementari che ne portano la carica. Queste comprendono i quarks
e otto portatori di carica, simili sotto certi aspetti ai fotoni, che vengono detti gluoni. Le forze
deboli sono più semplici da questo punto di vista (anche se violano parità e inversione
temporale) perché meno intense. La loro natura a corto raggio riflette la presenza nel vuoto di
un condensato, una sorta di melassa cosmica che rallenta ogni particella che la avverte, la cui
esistenza è stata rivelata in modo indiretto dalla scoperta del bosone di Higgs al CERN nel
2012. Le particelle elementari note sono anche accompagnate da corrispondenti antiparticelle,
con uguale massa e carica opposta (il positrone, antiparticella dell’elettrone, fu scoperto per
primo negli anni Trenta del secolo scorso). Tutte queste particelle si presentano in tre famiglie,
che si ripetono identiche ma con masse crescenti. Esse riempiono le caselle del Modello
Standard delle interazioni deboli, forti ed elettromagnetiche in modo simile, sotto certi aspetti,
a quanto avviene per gli atomi e la tavola periodica (Fig. 4). I portatori di forza, oltre al fotone,
sono i bosoni intermedi W e Z scoperti al CERN nel 1984, gli otto gluoni responsabili
dell’interazione forte, e il gravitone. Come vedremo, quest’ultima particella ha un ruolo molto
importante, ma a differenza delle altre non è stata ancora rivelata.
Fig. 4 – Particelle del Modello Standard
7
Mi preme sottolineare che si parla in realtà di interazioni, e non di forze, perché questo
concetto è più generale. Come abbiamo visto (Fig. 3), infatti, in un processo microscopico
alcune particelle possono disintegrarsi e altre possono materializzarsi. Fluttuazioni di quantità
di moto si traducono infatti, a volte, in fluttuazioni di energia dell’ordine di 𝑚𝑚𝑚𝑚 2 : nulla osta, in
Meccanica Quantistica, che una particella di massa m si dematerializzi, se altre prendono con
sé la sua carica elettrica e altri attributi.
5. Relatività Generale: problemi con la Meccanica Quantistica, stringhe e M-teoria
La Relatività Generale resta, ad un secolo dalla sua scoperta, un grande trionfo della
Fisica Teorica e dei principi di simmetria. La sua struttura sublima scoperte che hanno segnato
il XIX secolo, e che hanno coinvolto in prima linea matematici tedeschi del calibro di Karl
Friedrich Gauss e Bernard Riemann oltre agli italiani Gregorio Ricci-Curbastro, Tullio LeviCivita e Luigi Bianchi. Le sue equazioni legano il comportamento universale delle particelle
in un campo gravitazionale alla natura dello spazio-tempo, che si deforma come un tappeto
elastico in presenza di massa (Fig. 5). Esse contengono una serie di predizioni straordinarie,
tra cui l’esistenza delle onde gravitazionali che è stata confermata di recente.
Sorprendentemente, la struttura di queste equazioni esibisce anche profonde analogie con le
equazioni di Maxwell, che sono più semplici solo perché il principio di simmetria che sottende
ad esse, e anche alla conservazione della carica elettrica, è più semplice. Negli anni Cinquanta
del secolo scorso queste analogie hanno condotto ad una generalizzazione
dell’elettromagnetismo, nota come teoria di Yang-Mills, che è alla base delle interazioni deboli
e forti. I loro “fotoni” sono appunto i bosoni intermedi e i gluoni. Si parla anche, a volte, di
unificazione tra interazioni deboli e elettromagnetiche, perché le due vengono ricondotte, in
parte, ad un principio comune di questo tipo, mentre un principio simile ma ben distinto regola
le interazioni forti. Si parla invece di Grande Unificazione nei casi in cui vengono proposti
principi comuni per le tre interazioni deboli, forti ed elettromagnetiche. Queste ultime teorie
hanno un’implicazione drammatica: il decadimento del protone, e quindi di tutta la materia che
popola l’Universo. Ma si tratta al momento di speculazioni, e molte ricerche hanno dato, per
ora, risultati negativi.
Fig. 5 – La gravità curva lo spazio-tempo
Cerchiamo ora di illustrare la difficoltà che si incontra se si cerca di combinare la
Relatività Generale con la Meccanica Quantistica. Anzitutto, l’analogia tra la formula di
Coulomb e quella di Newton implica che le corrispondenti particelle, dette gravitoni, hanno
8
massa nulla. Inoltre ad alte energie le interazioni gravitazionali, se descritte dalla Relatività
Generale e dalla Meccanica Quantistica, divengono estremamente intense. Questo risultato
segue dall’analogia con la legge di Coulomb e dalla relazione di Einstein tra massa ed energia:
𝐸𝐸 2
𝑄𝑄 → 𝐺𝐺 𝑚𝑚 → 𝐺𝐺 � 2 �
𝑐𝑐
2
2
Il secondo passo riflette il fatto che, in una teoria completa, le masse (e quindi le energie di
riposo) saranno in generale sostituite dalle energie di particelle in moto generico. La
conseguenza di questo ragionamento semplice e ingenuo è però rilevante. Le interazioni
gravitazionali tra particelle, trascurabili alle energie in gioco nei fenomeni atomici o nucleari,
diventano in tal modo di intensità confrontabile con quelle elettromagnetiche all’energia di
Planck. Si tratta di un’energia enorme, pari a decine di miliardi di miliardi di volte l’energia di
riposo di un atomo di idrogeno, ma il problema appare comunque serio. Queste difficoltà hanno
anche condotto alcuni a proporre che la Meccanica Quantistica non si applichi in questi termini
alla gravità, ma questa opzione sembra del tutto innaturale.
La rapida crescita d’intensità di cui sopra implica, in una formulazione sui cammini à
la Feynman, la presenza di singolarità molto difficili da gestire, a meno che esse non si elidano,
quasi per magia, nella somma. Questo crea profondi dubbi sulla compatibilità della Meccanica
Quantistica con la gravità, e ha portato negli ultimi quarant’anni ad una teoria molto ambiziosa
nota come Teoria delle Stringhe. Brevemente, si abbandonano le particelle come enti
fondamentali sostituendole con piccolissime cordicelle, che interagiscono tra loro in modo
meno efficiente ad altissime energie (Fig. 6). Ma una volta introdotte le cordicelle, le teorie
risultanti, note come superstringhe, richiedono che il nostro Universo contenga altre sei
dimensioni spaziali, tanto piccole da essere precluse sia ai nostri sensi che ai più sofisticati
strumenti di misura di cui disponiamo.
Fig. 6 – Ad altissime energie le stringhe interagiscono in modo meno intenso delle particelle
Esiste un’analogia tra questo fenomeno tanto remoto e un’esperienza comune: quando
un’auto entra in galleria la radio perde il segnale, e questo avviene semplicemente perché la
sua lunghezza d’onda è maggiore dell’apertura della galleria. Allo stesso modo, poiché le
particelle si comportano come onde, ulteriori dimensioni più piccole delle lunghezze d’onda
delle particelle che riusciamo a produrre restano inaccessibili ad ogni nostro strumento.
9
Fig. 7 – Rappresentazione schematica dell’evoluzione cosmologica
Due ingredienti fondamentali di questa storia sono un’importante simmetria nota come
supersimmetria, in grado di connettere fermioni e bosoni in Fig. 4, e la sua elegante
combinazione con la gravità, detta supergravità, che definisce il comportamento di queste
superstringhe al di sotto dell’energia di Planck. Le ulteriori dimensioni non sono però l’unica
complicazione, perché queste teorie coinvolgono anche membrane di diverse dimensioni, uno
zoo di oggetti estesi che fluttuano in un vuoto con molte dimensioni. Un grande passo avanti è
stato compiuto con l’evidenza di un unico principio che sottende a tutte queste costruzioni,
detto M-teoria e la cui identificazione è dovuta in gran parte al fisico americano Edward Witten.
Purtroppo si tratta di un principio unico ma molto elusivo, tanto che lo stesso numero totale di
dimensioni, dieci o undici, non è del tutto definito. Abbiamo inoltre le equazioni di questa
incredibile teoria, ma solo in approssimazioni che non consentono di estrarne informazioni
molto dettagliate. Peraltro, anche se le equazioni sono uniche, esiste un’infinità di modi di
collegarle al nostro mondo a quattro dimensioni, per cui una “teoria del tutto”,
paradossalmente, non sembra generare predizioni univoche e verificabili sul nostro Universo.
Lo sviluppo tumultuoso della Fisica nel Novecento ha portato ad esperimenti sempre
più complessi, sofisticati, costosi e lunghi, e ad un’inevitabile separazione tra fisici teorici e
sperimentali. Anche per questo motivo servirà tempo, molto lavoro e molta umiltà per chiarire
se le idee straordinarie che sottendono a queste costruzioni, che hanno già stimolato sviluppi
profondi e inattesi in Matematica, meritano anche un posto tra le leggi della Fisica.
6. Cosmologia, inflazione e CMB
Vorrei concludere con un cenno sull’Universo e la sua evoluzione, ovvero sulla Cosmologia
(Fig. 7). Anzitutto, è proprio la natura discreta degli spettri atomici, alla quale ho accennato in
precedenza, che indica che le altre galassie si allontanano da noi. Le loro stelle emettono luce
che ne identifica i componenti, ma se questa viene analizzata si vede che le sue righe spettrali
sono “spostate verso il rosso”, ovvero corrispondono a lunghezze d’onda maggiori di quelle
10
che troveremmo, per gli stessi elementi, sulla terra. È una sorta di effetto Doppler cosmico, che
presenta analogie con quanto si può verificare nella comune esperienza: il fischio emesso da
un treno che si allontana appare infatti più grave di quello che riceveremmo se fosse fermo. Il
risultato fornisce quindi un’importante evidenza dell’espansione dell’Universo.
Fig. 8 – Distribuzione angolare delle piccole irregolarità del CMB.
Le equazioni della Relatività Generale ci consentono di seguire l’evoluzione a ritroso
nel tempo, e identificano un’epoca in cui tutto era più denso e caldo, al punto tale che gli atomi
ionizzati formavano una salsa che intrappolava la luce. In seguito, quando la temperatura si è
ridotta, questa luce primordiale ha iniziato a propagarsi liberamente, e oggi ci perviene come
un fondo cosmico a microonde, o CMB. Questa radiazione fossile, ad una temperatura di
appena 2.7 gradi sopra lo zero assoluto (ovvero di circa 270 gradi sotto lo zero Celsius), è stata
scoperta quasi per caso alla fine degli anni Sessanta del secolo scorso. Ci giunge in modo
essenzialmente identico da tutte le direzioni, consistentemente con l’isotropia e l’omogeneità
che associamo all’Universo, a parte piccolissime irregolarità sulle quali tornerò a breve (Fig.
8). Procedendo ancora a ritroso si incontra una singolarità, detta a volte Big Bang, che segna
l’origine di questa evoluzione durata circa 14 miliardi di anni. Non si capisce perché radiazione
con storie diverse, proveniente da punti in direzioni molto diverse che apparentemente non
sono mai venuti in contatto, debba comportarsi in modo tanto regolare.
Questa difficoltà viene oggi superata invocando un’opzione garantita dalla Relatività
Generale. Poiché la gravità è una forza attrattiva, l’espansione sembrerebbe inevitabilmente
decelerata, come il moto di un sasso lanciato verticalmente che rallenta a causa dell’attrazione
terrestre. Einstein si accorse però ben presto che la Relatività Generale consente anche un
effetto repulsivo, ottenuto introducendo nelle equazioni un nuovo termine detto costante
cosmologica. Invocando peculiarità del vuoto, viene ipotizzato che un tale effetto repulsivo si
sia innescato nei primi istanti dopo il big Bang, dando luogo ad una vorticosa accelerazione
che prende il nome di inflazione ma lasciando presto il passo ad un’espansione decelerata.
Questa teoria associa tutto l’Universo oggi osservabile ad una regione in origine molto piccola,
i cui punti sono stati in contatto causale, amplificata oltremodo dalla fase inflazionaria. Questo
passo elimina una serie di difficoltà, suscita alcuni interrogativi profondi, ma conduce anche
ad una predizione che ha trovato una conferma importante in studi recenti del CMB. Vorrei
11
concludere descrivendo brevemente questo risultato, che è anche una prima finestra concreta
sulla combinazione di gravità e Meccanica Quantistica con conseguenze osservabili.
La Meccanica Quantistica implica che, a causa del principio di indeterminazione, lo
spazio vuoto sia popolato da fluttuazioni incontrollabili. Ebbene, si può dimostrare che
l’inflazione stiracchia su distanze cosmiche queste fluttuazioni, cristallizzandole in
deformazioni dello spazio-tempo che favoriscono l’aggregazione di massa in certe regioni
rispetto ad altre. I loro effetti si traducono anche in una caratteristica delle piccole irregolarità,
dell’ordine di una parte per milione, che sono presenti nella temperatura del CMB (Fig. 8).
Questo meccanismo viene oggi ritenuto all’origine della formazione delle galassie, e la
predizione sulle irregolarità è stata confermata recentemente, con grande precisione, dai dati
raccolti dal satellite Planck! Peraltro, lo stesso satellite ha anche rivelato che il nostro Universo
è entrato, in epoca recente, in una nuova fase di lieve accelerazione.
V. MUKHANOV, Physical Foundations of Cosmology, Cambridge, Cambridge University
Press, 2005.
A. SAGNOTTI, Teoria delle Stringhe, in Enciclopedia della Scienza e della Tecnica (Roma,
Istituto dell’Enciclopedia Treccani, 2007).
S. WEINBERG, The Quantum Theory of Fields, Cambridge, Cambridge University Press,
1995, 1996, 2000.
Contributo agli Atti del Convegno su “Conoscenza, trascendenza e carità”
Università Lateranense, Roma, 26 maggio 2016
12