Trasformazione di calore in lavoro - web

1
Trasformazione di calore in lavoro: le macchine termiche
Lo schema di una macchina termica
Nello studio delle trasformazioni termodinamiche abbiamo visto che se forniamo calore a un gas
contenuto in un cilindro chiuso da un pistone scorrevole, il gas si espande compiendo lavoro; ma
una volta effettuata tale trasformazione esso non è più in grado di
produrre altro lavoro perché il pistone è giunto a fine corsa.
Ciò che interessa è produrre lavoro indefinitamente e in modo
continuativo, occorre quindi ridurre il volume del gas per riportare
indietro il pistone e permettergli di compiere altre corse nel cilindro.
Per riportare il gas alle condizioni iniziali di volume, pressione e
temperatura per poter compiere altro lavoro, bisogna sottrarre calore.
La trasformazione che il gas deve compiere è pertanto ciclica.
Una macchina termica è costituita da un cilindro con pistone mobile
contenente il gas, da una sorgente di calore ad alta temperatura Tc
(sorgente calda) e da una a minor temperatura Tf (sorgente fredda). Con il
termine sorgente di calore intendiamo un corpo la cui temperatura non varia
in seguito all’assorbimento o alla perdita di calore. Può essere un corpo dalla
grandissima capacità termica come il mare o l’atmosfera, o un sistema che
reintegra il calore acquistato o perso come un bruciatore o un frigorifero.
Una macchina termica funziona nel seguente modo: il gas
• assorbe calore (Qassorbito) dalla sorgente ad alta temperatura (Tc)
• compie lavoro meccanico
• cede del calore (Qceduto) alla sorgente fredda a temperatura Tf minore di
Tc per ritornare nelle condizioni iniziali.
Da qui il ciclo si ripete.
Il calore ceduto al corpo alla temperatura Tf non è più recuperabile dalla macchina per compiere
lavoro, quindi non tutto il calore assorbito si trasforma in lavoro utile. Poiché la macchina termica
compie trasformazioni cicliche, la variazione di energia interna ∆U è nulla e il lavoro utile L, o
lavoro compiuto, è uguale al calore scambiato con l’ambiente esterno: L = Qscambiato.
Il calore scambiato è dato da: Qscambiato = Qassorbito − Qceduto, da cui otteniamo:
L = Qassorbito − Qceduto
Calcoliamo il rendimento della macchina termica:
lavoro utile
L
η=
=
energia assorbita Qassorbito
Il rendimento è anche uguale a:
Q
− Qceduto
Q
L
η=
= assorbito
= 1 − ceduto
Qassorbito
Qassorbito
Qassorbito
Ne deriva che il rendimento η di una macchina termica è sempre minore di 1; il rendimento
percentuale η % è sempre minore del 100%.
Esempio 1 – Calcolo del lavoro compiuto in un ciclo e del rendimento di una macchina termica.
Una macchina termica assorbe dalla sorgente di calore ad alta temperatura 6,0 · 103 J e cede alla sorgente
fredda 4,5 · 103 J. Vogliamo calcolare il lavoro compiuto in un ciclo e il rendimento della macchina.
Scriviamo i dati del problema
Calore assorbito dalla sorgente calda
Qassorbito = 6,0 · 103 J
2
Calore ceduto alla sorgente fredda
Qceduto = 4,5 · 103 J
Incognite
Lavoro compiuto (o lavoro utile)
L
Rendimento
η, η %
Analisi e soluzione
Calcoliamo il lavoro compiuto con la formula:
L = Qassorbito − Qceduto = 6,0 · 103 J − 4,5 · 103 J = 1,5 · 103 J
Il rendimento è dato da: η =
1,5 ⋅ 10 3 J
= 0,25 . Il rendimento percentuale è: η % = 25%
60 ⋅ 10 3 J
Il ciclo di trasformazioni con il massimo rendimento: il Ciclo di Carnot
Il fisico francese Sadi Carnot (1796-1832) studiò da un punto di vista teorico la trasformazione
ciclica del calore in lavoro e ideò il ciclo termodinamico con il
rendimento più alto possibile.
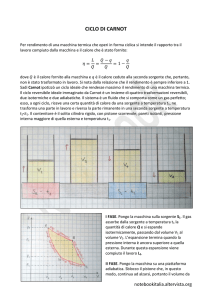
Tale ciclo, che porta il suo nome, è costituito da quattro
trasformazioni.
1^ trasformazione – Espansione isoterma alla temperatura più alta
Tc. Durante questa trasformazione il gas assorbe calore e, a
temperatura costante, si espande dallo stato A allo stato B
compiendo lavoro.
2^ trasformazione – Espansione adiabatica da B a C. Il gas non
assorbe né cede calore, ma continua ad espandersi. Compie
lavoro a spese della propria energia interna e la temperatura diminuisce fino a quella della
sorgente fredda Tf .
3^ trasformazione – Compressione isoterma da C a D. Il gas, cedendo calore alla sorgente fredda
alla temperatura costante Tf , viene compresso fino allo stato D.
4^ trasformazione – Compressione adiabatica da D a A. Il gas non cede né assorbe calore, ma
continua a comprimersi. Il lavoro di compressione si trasforma in energia interna aumentando la
temperatura del gas fino al valore iniziale Tc dello stato A.
Osserviamo come le trasformazioni che riportano il gas nello stato iniziale si trovano sul piano p-V
al di sotto di quelle che rappresentano l’espansione del gas. In questo modo il calore ceduto alla
sorgente fredda è minore di quello assorbito dalla sorgente calda e il lavoro utile, rappresentato
dall’area interna del ciclo, risulta positivo.
Le conclusioni cui giunse Carnot sono le seguenti:
• rispetto a una qualsiasi macchina termica che funzioni tra le stesse temperature, il ciclo di
Carnot ha il massimo rendimento possibile (chiamato quindi rendimento ideale)
• il rendimento di tale macchina risulta uguale a:
Tf
η = 1−
Tc
dove Tc e Tf sono le temperature assolute rispettivamente della sorgente calda e della sorgente
fredda
Sviluppo storico delle macchine termiche
Le macchine termiche capaci di trasformare in modo continuativo il calore in lavoro vennero
inventate durante la prima rivoluzione industriale in Inghilterra nel XVIII secolo. Furono costruite
dagli ingegneri inglesi Thomas Savery (1650-1715) e Thomas Newcomen (1663-1729) per poter
estrarre l’acqua dalle miniere di carbone. In seguito furono perfezionate dall’ingegnere scozzese
James E. Watt (1736-1819) e furono utilizzate nell’industria tessile e ferroviaria. Verso la fine del
3
1800 l’ingegnere inglese Charles Parsons (1854-1931) costruì la prima turbina a vapore, nella quale
il vapore faceva muovere direttamente le pale di una turbina senza
dover ricorrere al pistone.
Classificazione delle macchine termiche
Le macchine termiche si suddividono in:
• macchine a combustione esterna; in esse la produzione di energia
termica necessaria a riscaldare il fluido che compie il lavoro,
proviene da una caldaia esterna al motore. A questa categoria
appartengono:
- le macchine a vapore
- le turbine
• macchine a combustione interna; in esse la produzione dell’energia termica avviene all’interno
del motore stesso. Il fluido che espandendosi compie lavoro è costituito dai gas prodotti dalla
stessa combustione. A questa categoria appartengono:
- i motori a scoppio
- i motori a iniezione.
Descriviamo ora il funzionamento di alcune macchine termiche.
La turbina a vapore
Il calore prodotto dal bruciatore riscalda l’acqua della caldaia trasformandola in vapore ad alta
pressione. Questo vapore viene diretto contro le pale della turbina determinandone la rotazione. Il
vapore uscito dalla turbina è a bassa pressione e viene ritrasformato in acqua nel condensatore;
ritornato poi alla caldaia, riprende il ciclo. Il rendimento della turbina a vapore è dell’ordine del
45%.
La turbina a gas o turboreattore
Questa macchina termica è composta da tre parti: il
compressore d’aria, la camera di combustione e la
turbina posta sullo stesso asse del compressore.
L’aria entra dalla presa d’aria, viene compressa dal
compressore e aumenta di temperatura; entra nella
camera di combustione dove viene iniettato il
carburante (kerosene o benzina). Nella camera di
combustione la miscela aria-carburante, ad alta temperatura, esplode e i gas prodotti mettono in
rotazione la turbina che fa ruotare il compressore. I gas, superata la turbina, escono dagli ugelli a
velocità altissima provocando la spinta che fa avanzare il sistema su cui è montata la macchina.
Il motore a scoppio
Il motore a scoppio consiste di una camera cilindrica in cui può scorrere un pistone; essa è munita di
una candela e di due valvole: una per far entrare la miscela di aria e benzina, l’altra per lasciar
usciere i gas prodotti dalla combustione. La candela è formata da due elettrodi tra i quali può
scoccare una scintilla.
Nella prima fase di funzionamento del ciclo, quella di aspirazione, il pistone si abbassa e nel
cilindro entra attraverso la prima valvola la miscela aria-benzina, preparata nel carburatore. Nella
seconda fase, di compressione, il pistone si abbassa e comprime la miscela. Nella terza fase, di
accensione, scocca la scintilla che fa esplodere la miscela generando i gas che, ad alta pressione,
spingono in basso il pistone compiendo lavoro. Nella quarta fase, di scarico, il pistone si rialza ed
elimina i gas dalla seconda valvola. Per i motori a scoppio il rendimento è dell’ordine del 25 ÷ 30%.
Il motore a iniezione
4
Il motore a iniezione o motore diesel è molto simile al motore a scoppio; differisce da esso nel fatto
che le prime due fasi aspirano e comprimono solamente aria facendo raggiungere a quest’ultima
un’elevata temperatura; a questo punto viene iniettato il combustibile ridotto in minutissime
goccioline (polverizzato) che a contatto dell’aria calda si incendiano generando così i gas che
determinano la dilatazione compiendo lavoro. I vantaggi del motore a iniezione consistono nella
combustione completa del carburante e nella possibilità di utilizzare oli pesanti, quali la nafta e il
gasolio, meno costosi della benzina. Il suo rendimento può arrivare al 43%. il motore a iniezione
venne realizzato dagli inventori tedeschi Rudolf Otto (1832-1892) e Rudolf Diesel (1858-1913).
Frigoriferi, condizionatori d’aria e pompe di calore
La macchina termica durante un ciclo assorbe calore da una
sorgente calda, compie lavoro e cede una certa quantità di calore a
una sorgente fredda. Se facciamo funzionare la macchina in senso
contrario, la possiamo utilizzare come frigorifero. Il frigorifero
sfrutta il lavoro L compiuto dall’ambiente esterno sul gas per
trasferire a una sorgente calda (l’atmosfera esterna) una certa
quantità di calore Qf, sottratto a una sorgente fredda (la cella
frigorifera).
Indicata con Qc la quantità di calore trasmessa alla sorgente calda,
dal primo principio della termodinamica abbiamo:
Qc = Qf + L
Osserviamo come nella cucina si riversa una quantità di energia (Qc)
maggiore di quella (Qf) prelevata dall’interno del frigorifero. Perciò
il frigorifero raffredda i cibi e riscalda la cucina.
Il condizionatore d’aria è come il frigorifero: toglie calore dalla casa
e lo disperde nell’aria esterna.
La pompa di calore è un sistema di riscaldamento che funziona in senso inverso rispetto al
condizionatore: toglie calore dall’aria esterna e lo trasferisce all’interno della casa.
5
Verifiche di comprensione
1. Spiega perché, dopo che il gas ha compiuto un’espansione ed effettuato lavoro, occorre riportare
il gas nelle condizioni iniziali
2. Illustra come si può riportate nelle condizioni iniziali un gas contenuto in un cilindro dotato di
pistone mobile
3. Descrivi lo schema di funzionamento di una macchina termica
4. Scrivi la formula che calcola il rendimento di una macchina termica
5. Quali sono le trasformazioni del ciclo di Carnot?
6. Descrivi ognuna delle trasformazioni del ciclo di Carnot
7. Quali sono le conclusioni cui giunse Carnot nello studio dei cicli termodinamici
8. In quale secolo vennero costruite le prime macchine termiche
9. Descrivi la classificazione in cui si possono suddividere le macchine termiche
10. Descrivi il funzionamento della turbina a vapore
11. Descrivi il funzionamento del turboreattore
12. Descrivi il funzionamento del motore a scoppio
13. Descrivi il funzionamento del motore a iniezione
14. Descrivi lo schema di funzionamento del frigorifero
15. Illustra le differenze tra il frigorifero, il condizionatore e la pompa di calore
Verifiche di conoscenza
1. Quale delle seguenti affermazioni è corretta? Il gas utilizzato in una macchina termica
a. compie solo trasformazioni a pressione costante per poter compiere lavoro
b. compie solo trasformazioni adiabatiche per poter sfruttare le variazioni di temperatura al
fine di compiere lavoro
c. compie trasformazioni cicliche in modo da poter ritornare nello stato iniziale
2. Il rendimento ideale di una macchina termica è dato dalla formula:
t fredda
a. η = 1 −
t calda
T fredda
b. η = 1 −
Tcalda
T fredda
c. η = 1 −
T fredda
dove sono state indicate con lettere minuscole le temperature in °C, e con lettere maiuscole le
temperature in K
3. Le temperature che compaiono nella formula del rendimento devono essere misurate in:
a. kelvin
b. °C
c. indifferentemente in K o in °C perché la loro differenza è una costante (273,15)
d. in K se il gas è ideale, in °C se il gas è reale
4. Per raffreddare una stanza conviene metterci un frigorifero con la porta aperta?
a. Certamente, perché in questo modo il calore viene prelevato non solo dalla cella
frigorifera, ma anche da tutta la stanza
b. No, perché una stanza è troppo vasta e il consumo di energia elettrica sarebbe enorme
c. No, perché il calore riversato nella stanza sarebbe maggiore di quello sottratto
d. Sì, solo se il frigorifero è di quelli dell’ultima generazione
5. In quale dei seguenti casi un frigorifero non riscalda la stanza in cui si trova?
a. Se il frigorifero ha la porta chiusa
b. Se il frigorifero ha la porta aperta
c. Se il frigorifero è spento
6
Problema svolto – Calcolo del rendimento e del lavoro utile compiuto da una macchina termica che
segue il ciclo di Carnot
Una macchina ideale segue il ciclo di Carnot e opera tra le sorgenti alle temperature di 250 °C e 30 °C;
durante un ciclo assorbe 4,0 · 103 J. Vogliamo calcolare il rendimento della macchina e il lavoro utile
compiuto.
Scriviamo i dati del problema
Temperatura della sorgente calda: tc = 250 °C. Temperatura della sorgente fredda: tf = 30 °C
Calore assorbito in un ciclo: Qassorbito = 4,0 · 103 J
Incognite
Rendimento η della macchina termica. Lavoro utile L prodotto in un ciclo
Analisi e soluzione
Trasformiamo le temperature in gradi kelvin:
Tc = 250 °C + 273,15 = 523 K. Tf = 30 °C + 273,15 = 303 K
Calcoliamo ora il rendimento:
η =1−
303 K
= 0,421 ; η % = 42,1%
523 K
Calcoliamo il lavoro utile dalla formula η =
Problemi
Lutile
: L = η · Qassorbito = 0,421 · 4,0 · 103 J = 1,7 · 103 J.
Qassorbito
1. Una macchina termica assorbe dalla sorgente calda 2,0 · 103 J e cede alla sorgente fredda 1,3 ·
103 J. Calcola il lavoro compiuto e il rendimento percentuale della macchina.
2. Il lavoro compiuto da una macchina termica vale 9,8 · 103 J e il calore ceduto alla sorgente
fredda è 2,3 · 104 J. Determina il calore assorbito dalla sorgente calda e il rendimento
percentuale della macchina.
3. Una macchina termica ideale lavora tra le temperature: 90 °C e 270 °C. Calcola il rendimento
della macchina.
4. In una macchina termica ideale il calore assorbito dalla sorgente a temperatura di 350 °C, è di
8,0 · 103 J; la temperatura della sorgente fredda è di 100 °C. Determina il rendimento
percentuale della macchina e il lavoro compiuto.
5. Determina il rendimento di una macchina termica ideale che lavora tra le temperature: 80 °C e
300 °C. Sapendo che il lavoro compiuto vale 6,0 · 103 J, calcola il calore assorbito dalla
sorgente calda.
6. Il rendimento percentuale di una macchina termica ideale è del 36%. La temperatura della
sorgente calda è di 280 °C. Calcola in °C la temperatura della sorgente fredda.
7. La temperatura di una sorgente calda di una macchina termica ideale è di 220 °C e il rendimento
percentuale vale 28%; sapendo che il lavoro compiuto è di 3,6 · 103 J, calcola la temperatura in
°C della sorgente calda e il calore assorbito da essa.
8. Una macchina termica ideale presenta un rendimento del 30%. La temperatura della sorgente
fredda vale 93 °C. Calcola in °C la temperatura della sorgente calda. Per aumentare il
rendimento della macchina mantenendo la stessa temperatura della sorgente calda, occorre
aumentare o diminuire la temperatura della sorgente fredda?
9. Una macchina termica assorbe dalla sorgente calda 9,0 · 103 J e compie un lavoro di 3,0 · 103 J.
Calcola il calore ceduto alla sorgente fredda, il rendimento della macchina e il rapporto tra la
temperatura della sorgente fredda e quella della sorgente calda.
10. Una macchina termica reale lavora tra le temperature: 50 °C e 200 °C. Sapendo che il suo
rendimento reale è il 60% di quello ideale, calcola il rendimento ideale e quello reale della
macchina. Questa poi assorbe una potenza di 30 kW dalla sorgente calda; calcola la potenza
utile.