Il secondo principio della
termodinamica
Si è incazzato perchè non è arrivato
primo.
capita
Pierluigi Rizzuti
Igor Tarantino
Giuseppe Fichera
Andrea Mincuzzi
Primo principio
• Il primo principio afferma che in una macchina termica il
calore assorbito è uguale alla somma del lavoro svolto e il
calore ceduto all’esterno:
|Q2|=|Q1| + L
Usiamo i valori assoluti per evitare confusione con i segni.
Possiamo dire che il calore Q2 assorbito dalla sorgente
calda è uguale alla somma del lavoro L e della quantità di
calore Q1 ceduto alla sorgente fredda.
Questo principio è fondamentale per tutto quello che seguirà
Carnot
Nel 1824, prima degli
esperimenti di Joule, il
francese Sadi Carnot, volle
teorizzare il funzionamento
delle macchine termiche, che
fino a quel momento
funzionavano empiricamente,
per superare l’inghilterra nella
lotta all’industrializzazione.
Voleva migliorare il cosiddetto
RENDIMENTO
Egli tuttavia partiva dal concetto
errato che il calore fosse un
fluido che si conservava
attorno ai corpi (teoria di
Laplace e Lavoisier)
Rendimento di una macchina Termica
• Il rendimendimento η di una macchina termica è
definito come il rapporto tra il lavoro compiuto dalla
macchina e la quantità di calore assorbita:
• η=L/Q
• Dato che lavoro e calore sono grandezze fisiche
equivalenti, il rendimento è un numero adimensionale
• Al’epoca di Carnot le più efficienti macchine avevano
un rendimento intorno al 10%; il resto del calore era
disperso nell’ambiente.
La macchina ideale e le conclusioni
• Carnot quindi ideò su questo concetto una macchina ideale, che
non lasciava disperdere il calore all’esterno.
• Egli capì per primo il concetto che, come l’acqua di un mulino
sfrutta l’energia potenziale per azionare la turbina, così,
sfruttando la differenza di calore, il lavoro veniva compiuto in
una macchina termica.
• Tuttavia egli credeva che il calore non venisse assorbito dalla
macchina e si disperdesse intero nell’ambiente
• IN QUESTO MODO SAPPIAMO CHE SE VOGLIAMO CONVERTIRE
IL CALORE IN LAVORO, BISOGNA PER FORZA CEDERE CALORE
ALLA SORGENTE FREDDA, QUINDI IL RENDIMENTO SARA’
SEMPRE MINORE DI 1
• Il rendimento quindi aumenta all’aumentare del dislivello
termico
Lord Kelvin
• E’ impossibile realizzare una trasformazione
termodinamica il cui unico risultato sia quello di
assorbire una quantità di calore da una sorgente
termica e convertirlo integralmente in lavoro.
• Da questo possiamo capire che se tutto il calore
assorbito viene convertito in lavoro, ci sarà per forza
un’altra conseguenza:
• In una macchina isoterma per esempio possiamo
capire dal primo principio:
• ΔU = Q – L → Q = L
• In questo caso, infatti, il lavoro viene compiuto
dall’espansione di un gas, e l’equivalente di
quell’energia sottoforma di calore è diretto verso la
sorgente fredda. In questo caso quindi abbiamo come
risultato finale anche l’espansione del gas.
Clausius
• E’ impossibile realizzare una trasformazione
termodinamica il cui unico risultato sia quello
di trasferire una quantità di calore da un corpo
a temperatura minore ad uno a temperatura
maggiore.
• Noi staremo pensando adesso al frigorifero,
che prende energia dall’interno e la trasferisce
all’esterno. Questo non ci deve trarre in
inganno, dato che questo processo è compiuto
grazie ad un altro lavoro, in questo caso, la
corrente elettrica
• Questi due enunciati sono
equivalenti, infatti se è falso
uno, sarà falso anche l’altro
• Se fosse falso quello di
Clausius potremmo
trasferire calore da una
sorgente calda ad una
fredda e compiere lavoro, e
poi sfruttare il calore
trasferito a quella fredda
per trasferirla di nuovo a
quella calda, facendo sì che
tutto il calore sia utilizzato
per compiere lavoro
Macchina Anti-Clausius
• Se fosse falso quello di
Kelvin potremmo
utilizzare l’energia di
una sorgente calda
per mettere in moto
un mulinello di Joule
con i pesi abbassati e
riscaldare l’acqua
all’interno facendola
diventare più calda
della sorgente iniziale.
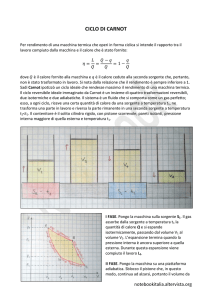
Dal ciclo di Carnot ricaviamo che il lavoro è
uguale alla differenza dei valori assoluti delle
quantità di calore Q2 e Q1 e rispettivamente
assorbita e ceduta dalla macchina:
L = |Q1| - |Q2|
η = L/|Q2| = (|Q1| - |Q2|)/|Q2|
η = 1 - |Q1/Q2|
• Il rendimento η di una macchina termica M è sempre
minore o uguale al rendimento ηrev di una macchina Mrev
reversibile che operi fra le stesse temperature, dove il
segno di uguaglianza vale solo se la macchina M è
reversibile.
• Cioè:
η ≤ ηrev
• Una macchina termica reversibile ha al proprio interno
solo processi reversibili.
• Perchè un processo sia reversibile devono essere
soddisfatte 3 condizioni:
1. La trasformazione deve essere quasistatica
2. Non vi devono essere attriti
3. Il sistema deve scambiare calore soltanto con sorgenti
ideali di calore
Si capisce che una macchina reversibile sia IDEALE
• I risultati ottenuti non fanno riferimento al tipo di
gas, quindi possiamo utilizzare un gas perfetto
per semplificare i calcoli.
• Si può dimostrare che una macchina di Carnot
che lavora tra due temperature T1<T2 ha
rendimento ηrev = 1 – T1/T2.
• QUINDI IL RENDIMENTO DI UNA MACCHINA
REALE E’:
• η ≤ 1 – T1/T2
• OVVERO, IL RENDIMENTO MASSIMO DIPENDE
SOLTANTO DALLE TEMPERATURE DELLE
SORGENTI
Come tutte le cose vanno deteriorandosi (vedi
monumenti), ogni processo naturale tende ad andare
verso un’unica direzione determinando un’asimmetria
nella natura: infatti, ponendo il limite alla conversone di
calore e lavoro, qualsiasi oggetto prima o poi si ferma a
causa del lavoro delle forze d’attrito, scaldandosi. Non
esiste il processo inverso.
Questa asimmetria è quantificata da una nuova grandezza
fisica, l’entropia, che individua la direzione delle
trasformazoni termodinamiche e si accorda con ciò che
percepiamo come lo “scorrere del tempo”
Ad esempio in natura è impossibile che da un sistema
“disordinato” contenente acqua liquida si passi ad uno
“ordinato” di acqua e ghiaccio, oppure che una pallina
inizi a rotolare prendendo energia dall’ambiente.