COMPITI DELLE VACANZE DI FISICA
PER IL BIENNIO
Le grandezze fisiche: notazione scientifica, ordine di grandezza, equivalenze, formule
inverse
1. Determina la notazione scientifica dei seguenti numeri:
0,04
0,000035
929 10 12
0,00005 10 6
800
86400
0,002 10 20
1miliardo
900 1010
2. Esegui le seguenti equivalenze, dopo aver espresso le grandezze in notazione scientifica:
0,12m m
20km m
7,1cm 3 m 3
30m 2 km 2
6,3s ns
15cg g
2
2
1,5ms s
0,2kg hg
100m cm
0,1mg g
1g t
2h 20 min s
3. Trasforma nel S.I. le seguenti misure e indicane il rispettivo ordine di grandezza:
Misura
Misura in notazione
scientifica
Misura nel
S.I.
Ordine di grandezza
950000Km
8700mg
1000 m
12ms
4. Un contenitore a forma di parallelepipedo rettangolo ha le dimensioni di 40,0cm, 0,200m e
20,0cm. Calcolare il volume in m3, cm3, mm3.
5. Quanti picosecondi ci sono in un minuto?
Quanti secondi ci sono in tre giorni?
6. Le masse del Sole e della Terra sono rispettivamente 1,98 10 30 kg e 5,98 10 24 kg . Qual è
l’ordine di grandezza del loro rapporto?
7. Date le seguenti leggi fisiche, ricava le grandezze a fianco indicate:
s
1 2
a) v
s=........; t=........
b) s gt
g=.......; t=.........
t
2
q1 q 2
k=....... ; r=........
d) v v0 at
s0=.......; t=.........
r2
8. Il raggio di una sferetta di acciaio (la cui densità è 7800 kg/m3) misura 1,5cm. Qual è la massa
della sferetta?
9. Perché 1g/cm3 corrisponde a 1000kg/m3?
c) F k
Elaborazione dei dati sperimentali: errori nelle misure dirette e indirette
1. Due sperimentatori, adoperando un cronometro che permette di apprezzare 1/10 di secondo,
trovano come misura del periodo di oscillazione di un pendolo 1,12s, 1,3s e 1,214s. Sono
attendibili tutte e tre le misure? Se no quale misura è più attendibile? Spiega perché.
2. I risultati di una misura, realizzati con uno strumento di sensibilità pari a 0,1mm e
determinati con la calcolatrice, sono i seguenti: media = 25,364mm, semidispersione =
0,175mm. Scrivi correttamente il risultato della misura.
3. Tre misurazioni di lunghezza hanno dato i seguenti risultati:
200 4cm; 1645 9cm; 45 1cm.
Quale delle tre misure è più precisa? Motivare la risposta.
4. La misura di una massa è 205 4 g . Se la stessa misura è espressa in milligrammi quanto
vale l’errore assoluto? Viene alterato l’errore percentuale cambiando l’unità di misura? E
quello relativo?
5. Supponi di aver effettuato 27 volte la misura del periodo di oscillazione di un pendolo con
un cronometro al centesimo di secondo e di aver ottenuto i risultati riportati in tabella:
frequenza periodo(s) frequenza Periodo(s)
1
0,66
2
0,71
2
0,68
5
0,72
3
0,69
5
0,74
3
0,70
6
0,75
Determina il valore medio della misura del periodo, l’errore assoluto, l’errore relativo e
l’errore percentuale.
Leggi di propagazione degli errori
6. Per determinare il volume di un corpo di forma irregolare lo si immerge in un recipiente
cilindrico pieno di acqua avente la sezione di 15,6 0,3cm 2 . Tenendo presente che il
livello dell’acqua si innalza di 1,4 0,1cm , esprimere la misura del volume del corpo con
l’indicazione dell’errore. (Suggerimento: volume corpo= variazione volume acqua).
7. Le misure della lunghezza e della larghezza di un tavolo rettangolare sono 1,6m e 0,9m con
l’errore del 2%. Calcolare l’errore assoluto di ciascuna misura. Calcolare la misura del
5,0 0,1m; 1,44 0,06m 2
perimetro e dell’area con l’errore assoluto.
8. Le misurazioni delle dimensioni di un corpo, avente la forma di un parallelepipedo
rettangolo, hanno dato i seguenti risultati:
24,50 0,05mm; 12,70 0,05mm; 16,85 0,05mm
Calcola il volume del corpo con l’errore assoluto.
Relazioni fra grandezze fisiche
1 Scrivi la relazione esistente fra le seguenti coppie di grandezze e la corrispondente legge
matematica:
Circonferenza e raggio di un cerchio.
Base b e altezza h di un rettangolo di area fissata 30m2
Velocità media v e tempo t di un atleta che percorre un tratto di 100m
Diagonale e lato di un quadrato
Area e raggio di un cerchio
2
La tabella seguente riporta il volume e la massa di quantità variabili di alcol. Scrivi la legge
matematica che lega la massa m e il volume V; traccia il grafico.
Cosa rappresenta la costante di proporzionalità della relazione da un punto di vista grafico
e fisico? Determina dal grafico la massa di alcol che occupa il volume di 22,5cm3
(interpolazione).
Determina infine, prolungando il grafico, la massa di alcol che corrisponde a un volume di
45 cm3 (estrapolazione).
3
VOLUME (cm )
5
10
15
20
25
3
MASSA (g)
4,0
8,0
12,0
16,0
20,0
Con uno stesso volume di liquido, pari a 50 cm3, riempiamo alcuni recipienti
cilindrici di diametro variabile. Il liquido raggiunge ogni volta un’altezza diversa. Compila
la seguente tabella relativa all’esempio descritto.
Qual è la legge che esprime la relazione fra A e h? Fai la rappresentazione grafica.
2
Area di base A (cm )
10
20
30
40
50
Altezza liquido h (cm)
5,0
4
Ho corso per 2km e ho consumato 180kcal. Quanto consumo quando corro per 6km?
5
La relazione fra le grandezze x e y è descritta dal grafico seguente.
Y
9
3
X
12
Di che tipo di relazione si tratta? Quanto vale il rapporto (costante) fra un aumento di x e il
corrispondente aumento di y? Scrivi la legge che esprime la relazione.
Vettori
1. Il vettore a punta nel verso positivo dell’asse y e ha un modulo di 12 unità. Il vettore b ha
modulo pari a 1/3 di quello di a e punta nel verso negativo dell’asse x. Rappresenta
graficamente i vettori a b , b a , a 3b e calcolane il modulo. Esprimi direzione e verso
del vettore a 3b .
2. Un aereo si muove in direzione Est 30° Sud. Se la componente dello spostamento in
direzione Est è 10Km quanto vale il modulo del suo spostamento? E la componente dello
spostamento in direzione Sud?
3. Un battello che collega le località di un lago, parte dalla città A, raggiunge B
spostandosi di 12Km in direzione Nord 45° Est, prosegue a Nord per 10Km fino a C, e
da qui raggiunge D che si trova 3,5Km a Ovest. Rappresenta graficamente la situazione
e calcola il modulo dello spostamento risultante tra A e D.
4. Due forze, applicate nello stesso punto, di modulo F1 60 N e F2 30 N formano un
angolo di 60°. Dopo aver disegnato le forze in scala in un opportuno sistema di
riferimento, calcola il modulo della loro risultante
(applica
il metodo delle componenti
cartesiane). Disegna poi una terza forza tale che F1 F2 F3 0 .
Equilibrio dei corpi solidi
1. Ad un anello sono applicate due forze che formano un angolo di 45°, l’una di intensità
3N e l’altra di 4N. Perché l’anello non è in equilibrio? Rappresenta graficamente i vettori
e determina direzione, verso e intensità dell’equilibrante.
2. Una lampada di massa 2,5Kg è appesa attraverso un filo ad una trave di legno. Quali
forze agiscono sulla lampada e qual è la loro intensità? Rappresentale con un disegno.
Se il filo ha una costante elastica di 2500N/m, di quanti mm si allunga sotto il peso della
lampada?
3. Una molla di acciaio di costante elastica 500N/m viene compressa da una forza di 150N.
Se inizialmente la molla era lunga 0,58m, qual è la sua lunghezza finale?
4. Una scatola di 3,0 kg è poggiata sul piano di un tavolo. Viene spinta con una forza parallela
al piano. La scatola comincia a muoversi quando la forza vale 30N. Fai un disegno per
illustrare le forze agenti. Qual è il coefficiente di attrito statico? Se poggiamo sulla scatola
un’altra della stessa massa, qual è il coefficiente di attrito statico?
5. Per tenere in equilibrio una scatola di cioccolatini su un piano inclinato liscio lungo
50,0cm e alto 22,5cm occorre una forza di 3,97N. Rappresenta le forze agenti. Ricava il
peso della scatola.
6. Un corpo del peso di 9,0N, è posto su un piano inclinato liscio lungo 40cm e alto 20cm; a
esso è applicata una forza di 4,0N, parallela la piano, e diretta verso l’alto. Stabilisci se il
corpo resta in equilibrio.
7. Un blocco è appoggiato su un piano inclinato di 30 0. Il blocco è mantenuto in equilibrio
dalla forza di attrito statico avente modulo di 30N. Rappresenta le forze agenti. Qual è il
peso del blocco? Qual è la componente del peso perpendicolare al piano inclinato? Quanto
vale il coefficiente di attrito statico?
8. Si vuole sollevare di 2,0m un oggetto che pesa 15N. La forza a disposizione è di poco
superiore a 3,0N. Che lunghezza deve avere il piano inclinato su cui si effettua il
trasporto? Quanto vale la reazione vincolare del piano?
[10m]
9. Una coppia di forze, ognuna di valore 50,0N, è applicata agli estremi di un’asta lunga
80,0cm, vincolata nel centro. Quanto vale il momento della coppia se le forze sono applicate
perpendicolarmente all’asta? E se sono applicate a 60° rispetto all’asta? Fai un disegno e
individua il braccio della forza in ciascun caso.
[40Nm; 35Nm]
10. Ad una ruota di raggio 0,40m, vincolata al centro, viene applicata una forza di 20N in
direzione perpendicolare a quella radiale. Oltre a tale forza, quale altra forza agisce sulla
ruota? Quanto vale la risultante delle forze agenti? La ruota è in equilibrio? Spiega. Calcola
il momento di rotazione della forza che agisce sulla ruota.
[La reazione del vincolo; no; 8,0Nm]
11. Ad un’estremità di un’asta lunga 1,0m, che può ruotare attorno ad un’asse passante per il
suo centro, inizialmente in equilibrio in posizione orizzontale, viene appeso un corpo di
2,7N. Che forza deve essere applicata ad un gancio, che si trova alla distanza di 30cm dal
centro dalla parte opposta, per mantenere l'asta in equilibrio?
[4,5N]
12. Verifica che l’asta in figura non è in equilibrio. Dove devo mettere un peso di 20N per
equilibrare l’asta?
[A 10cm del fulcro a destra]
Equilibrio dei fluidi
1. Una donna che pesa 650N porta scarpe con i tacchi a spillo; ogni tacco ha una superficie di
1, 0cm 2 . Che pressione esercitano i tacchi delle scarpe sul pavimento?
2. Un elefante ha un peso di 5, 0 ×104 N e ciascuna delle sue zampe ha una superficie di circa
0, 05m 2 ; la pressione che esercita sul terreno è maggiore o minore di quella dei tacchi della
donna?
3. Una cassa di 100N poggia su una superficie di 0,60m 2. Quale pressione esercita se è appoggiata
su una superficie orizzontale? E se è appoggiata su un piano inclinato di 30°?
4. A quale profondità nel mare la pressione è pari al doppio di quella atmosferica?
5. Cambierebbe in modo rilevante il risultato dell’esercizio precedente se invece del mare
considerassimo un tubo di piccolo diametro, pieno d’acqua e alto 10m?
6. In un rifugio a 2500m d’altitudine la colonnina di mercurio di un barometro di Torricelli rimane
stabile a 59cm di altezza. Quanto vale la pressione atmosferica? ( densità mercurio=13,6g/cm3)
7. Una sferetta di rame ( d = 9, 0g/cm3 ) ha un volume di 10cm3 ; determinarne il peso apparente
della sferetta, quando è completamente immersa in acqua e quando è completamente immersa in
un olio di densità 0,80g/cm3 .
8. Uno studente per misurare la densità di un liquido, appende ad un dinamometro un cilindretto di
acciaio ( d = 7, 0 g / cm3 ) di 500g; lo strumento, quando il cilindretto è completamente immerso
nel liquido segna 3,96N . Qual è la densità del liquido?
I MOTI RETTILINEI
1. In una gara multipla un atleta percorre 25km in bicicletta nel tempo di 45min. Successivamente
nuota in un tratto di fiume per 200m impiegando 360s infine corre per 3000m in un tempo di
8min e 57s. Quanto vale la velocità media complessiva in Km/h?
2. Con un’automobile percorri prima 4,00km a 30,0km/h e poi altri 4,00km a 50,0km/h. Quanto
vale la velocità media per il tragitto totale di 8,00km?
3. In una strada trafficata guidi un’automobile in linea retta a 12m/s per 1,5min, poi rimani fermo
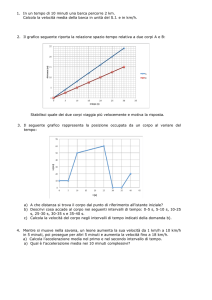
per 3,5min e infine procedi a 15m/s per altri 2,5min. Disegna il grafico posizione – tempo per
questo moto relativo all’intervallo di tempo fra t=0 e t=7,5min. Usando il grafico calcola la
velocità media tra t=0 e t=7,5min.
4. Le onde radio viaggiano alla velocità della luce,
approssimativamente 300000km/s. Quanto tempo impiega un
messaggio radio inviato dalla Terra per raggiungere la Luna e
tornare sulla Terra?
( Cerca i dati necessari )
5. I grafici in figura rappresentano il moto di due automobili che
si muovono di moto rettilineo uniforme. Calcola la velocità e
scrivi la legge oraria di ciascuna automobile. Calcola gli
istanti di tempo in cui le due automobili si trovano alla
distanza di 1,0km.
6. Le leggi orarie di due ciclisti che percorrono la stessa strada dritta sono: s A (t) = 50 - 20t e
s B (t) = 12,5t con t espresso in h e s in km. Disegna sullo stesso piano cartesiano i due
diagrammi orari e calcola dopo quanto tempo dalla partenza si incrociano.
7. Un treno che sta viaggiando su un tratto rettilineo con una velocità iniziale di 0,50m/s, accelera
di 2,0m/s2 per 2,0s, prosegue con velocità costante per altri 3,0s e quindi decelera di -1,5m/s2 per
1,0s. Disegna il grafico velocità – tempo nell’intervallo tra t=0 e t=6,0s. Qual è la velocità finale
del treno? Qual è l’accelerazione media del treno?
8. Un’automobile procede alla velocità di 72km/h e a un certo punto comincia a rallentare con
un’accelerazione costante di -2,0m/s2. Calcola la velocità dell’automobile dopo 3,5s e lo spazio
percorso.
9. Un treno viaggia ad una velocità di 180km/h, poi frena e si ferma in 15s. Quanto vale la sua
accelerazione? Qual è lo spazio di frenata?
10. Stai guidando il tuo motorino in città alla velocità di 12m/s, quando vedi un cane fermo in
mezzo alla strada davanti a te. Azioni i freni e cominci a decelerare di 3,5m/s 2. Quale distanza
percorri prima di fermarti?
11. Con una fionda, un bambino lancia un sasso verticalmente verso l’alto dall’altezza di 1,0m dal
suolo. La velocità iniziale del sasso è 10m/s. A quale altezza massima arriva e in quanto tempo?
Dopo quanto tempo dal lancio il sasso tocca terra?
LA DINAMICA
1. Un falegname spinge un armadio di 80Kg su un pavimento di legno. Il coefficiente di attrito
è 0,20; la forza esercitata è parallela al pavimento, vale 200N ed è costante. Con quale
accelerazione si muove l’armadio? Qual è lo spostamento dell’armadio in 5,0s, se
inizialmente era fermo?
2. In un cantiere una gru solleva un blocco di cemento di massa 200Kg con un’accelerazione
costante pari a 0,550m/s2. Qual è la forza risultante che agisce sul blocco? Qual è l’intensità
della forza applicata dalla gru sul blocco? Per tirarlo su a velocità costante la gru dovrebbe
impiegare una forza maggiore o minore? Perché?
3. Ad una biglia di 100g viene impressa una velocità iniziale di 0,5m/s su una pista di sabbia.
Calcola l’intensità della forza di attrito che agisce costantemente sulla pallina sapendo che
questa si ferma dopo aver percorso 1,2m.
4. Un’automobile ha una massa di 900Kg e sta trainando un piccolo rimorchio. Il suo motore le
imprime un’accelerazione pari a 2,4m/s2. Ad un dato istante il rimorchio si stacca e
l’accelerazione passa bruscamente al valore di 3,3m/s2. Qual è la massa del rimorchio?
5. Un bimbo spinge uno slittino di 10Kg su un lago ghiacciato con una forza di 20N. Sua
sorella, per dispetto, tira in verso contrario. Supponendo trascurabile l’attrito, se in 5 s il
bambino riesce a spostare lo slittino inizialmente fermo di 1 m, qual è l’intensità della forza
esercitata dalla sorella?
6. Un bambino di massa 28kg scende lungo uno scivolo alto 2,40m e lungo 3,60m.
Supponendo trascurabile l’attrito, con quale accelerazione scende il bambino? In quanto
tempo e con quale velocità arriva in fondo allo scivolo? Se l’attrito non fosse trascurabile
come cambierebbero le risposte alle domande precedenti?
7. Una slitta è trascinata su un lago ghiacciato (attrito trascurabile) da una muta di cani. Nel
suo insieme, la muta esercita una forza costante di valore pari a 1400N. La slitta acquista
velocità con un’accelerazione di 0,72m/s2. Quale accelerazione subirebbe la slitta se la forza
costante esercitata dalla muta fosse ridotta a due terzi di quella precedente?
8. Un disco a ghiaccio secco, di massa 0,20kg, è appoggiato su una superficie piana orizzontale
ur
uur
priva di attrito e su di esso agiscono le tre forze F1 diretta nel verso positivo dell’asse x, F2
uur
diretta nel verso positivo dell’asse y e F3 diretta nel verso negativo dell’asse x,
rispettivamente di moduli 12N, 12N e 4,0N e tutte parallele alla superficie. Determina
l’accelerazione del disco in modulo e direzione.
9. Un motociclista sta per affrontare una curva. Il coefficiente di attrito tra i pneumatici e la
strada è 0,70 e il raggio della curva è 25m. Qual è la massima velocità a cui il motociclista
può effettuare la curva?
IL MOTO IN DUE DIMENSIONI
MOTO DEL PROIETTILE - MOTO CIRCOLARE UNIFORME
1.
Un cannone, piazzato su una collina alta 100m, spara orizzontalmente un proiettile con una
velocità di uscita di 300m/s. Trascurando la resistenza dell’aria, in quanti secondi il proiettile
tocca terra? A quale distanza dalla base della collina il proiettile tocca terra? Si disegni la
traiettoria del proiettile (scrivi l’equazione della corrispondente parabola e rappresentala nel
piano cartesiano).
2. Un cannone spara un proiettile lungo una direzione inclinata di 30 0 rispetto all’orizzontale, con
una velocità iniziale di 420m/s. Trascurando la resistenza dell’aria, quanto tempo impiega il
proiettile a toccare terra? Qual è l’altezza massima raggiunta? Qual è la gittata?
3. Un aereo che vola orizzontalmente a 576km/h e a una quota di 2000m, lancia un carico che deve
toccare terra in un punto ben preciso. Trascurando la resistenza dell’aria, a quale distanza
orizzontale dal bersaglio deve sganciare il carico? Quanto tempo prima di passare sulla verticale
del bersaglio l’aereo deve effettuare il lancio?
4. Calcolare il tempo di volo di un proiettile sparato obliquamente a 60 0 rispetto all’orizzontale
con velocità di modulo 49 3 m/s. Con quale velocità arriva al suolo?
5. Possiamo assumere che il Sole si muova di moto circolare uniforme attraverso la Via Lattea. Il
raggio dell’orbita solare è 2,4 10 20 m e la sua frequenza è di 1 giro ogni circa 220 milioni di
anni. Calcola l’accelerazione centripeta del Sole. Qual è il modulo della velocità del Sole?
6. Una pattinatrice rotea su se stessa compiendo 42 giri al minuto. Durante l’esecuzione, tiene i
gomiti verso l’esterno: la distanza fra i gomiti è di 0,60m. Quali sono la frequenza e il periodo
del moto della pattinatrice? Con quale velocità e con quale accelerazione si muovono i gomiti
della pattinatrice?
7. Un elicottero sta scaldando il motore, e le pale, ciascuna di 5,70m di lunghezza, ruotano a una
velocità angolare di 6,28 rad/s. Un’ape è appoggiata su una delle pale a 3,00m dal rotore. Qual è
l’accelerazione centripeta dell’ape? L’ape si sposta fino all’estremità della pala e scivola. Con
quale velocità viene proiettata lontano?
8. Nel passare il pallone a un compagno, un giocatore di pallacanestro descrive con il braccio un
arco di circonferenza di ampiezza 60,0 0 in 0,750s, a velocità approssimativamente costante. La
lunghezza del braccio del giocatore è di 80,0cm. Calcola con quale velocità viene lanciato il
pallone. Qual è il valore dell’accelerazione centripeta impressa al pallone durante la rotazione?
SOLUZIONI
EQUILIBRIO DEI FLUIDI
6,5 ×106 Pa
1.
1, 0 ×106 Pa
2.
1, 7 ×10 2 Pa ; 1, 4 ×102 Pa
3.
4.
10m
5.
No
7,9 ×104 Pa
6.
7.
0,72N; 0,80N
1,3g/cm3
8.
I MOTI RETTILINEI
1 28,2km/h
2 37,6km/h
3 7,4m/s
4 2,56s
5 25m/s; 8,3m/s; 60s; 180s
6 1,5h
7 3,0m/s; 0,42m/s2
8 13m/s; 58m
9 -3,3m/s2; 380m
10 21m
11 1,0s; 6,1m; 2,1s
LA DINAMICA
1. 0,54m/s2, 6,8m
2. 110N; 2, 07 ×103 N
3. 0,01N
4. 3, 4 ×102 kg
5. -19,2N
6. 6,53m/s2; 1,05s; 10,3m/s
7. 0,48m/s2
8. 14N
9. 13m / s
IL MOTO IN DUE DIMENSIONI
4,5s; 1,35 10 3 m; y 5,45 10 5 x 2
1.
2.
42,8s; 2,25 10 3 m; 1,56 10 4 m
3.
4.
3,23 10 3 m; 20,2s
15s
5.
2,1 10 10 m / s 2 ; 2,3 10 5 m / s
6.
0,70 Hz; 1,4 s; 1,3m / s; 5,8m / s 2
7.
118m / s 2 ; 35,8m / s
8.
1,12m / s; 1,56m / s 2