Non domandarci la formula che mondi possa aprirti
Sì una storta sillaba e secca come un ramo
Codesto solo oggi possiamo offrirti
Ciò che non siamo, ciò che non vogliamo (Montale)
Leggi della dinamica
Antonio Scafuro – [email protected] –– Roberto Chiumiento – [email protected]
www.antonioscafuro.it
Sommario: presentiamo con questo intervento un’esposizione delle leggi della
dinamica utilizzando alcuni strumenti che la tecnologia informatica mette a
disposizione. Gli strumenti che utilizziamo sono web-based, cabri e cabrijava. Con
cabri abbiamo costruito i modelli grafici dinamici che riproducono i fenomeni
descritti, cabrijava ci consnte di trasformare i modelli in applet e l’html di
visualizzare le applet come pagine web.
Prima legge della dinamica
Formulata da Galilei suona così: “Un corpo non soggetto a forze persevera nel suo stato di quiete o
di moto rettilineo uniforme” . Nella nostra presentazione c’è una prima pagina in cui viene mostrato
un carrello che, non soggetto ad alcuna forza, si muove di moto rettilineo uniforme.
Figura 1. Sul carrello non agisce alcuna forza
In questa applicazione è possibile cambiare il valore della velocità e, animando il punto t, osservare
in corrispondenza il moto del carrello, comunque in regime d’inerzia.
Quali sono le parti importanti di questa costruzione?
1) Un vettore orizzontale T sul quale si muove un punto t, che rappresenta il tempo che scorre
2) Una retta orizzontale, r, che rappresenta la strada sulla quale si muove il carrello
3) Un riferimento O su r
4) Il carrello
5) Le ruote del carrello
6) Il vettore orizzontale, che opportunamente scalato, rappresenta la velocità del carrello
Come funziona il modello?
1) L’ascissa di t su T fornisce il valore del tempo in secondi
2) L’ascissa dell’estremo libero di v fornisce il valore della velocità, in m/s
3) La calcolatrice ci consente di calcolare il valore della posizione dl baricentro del carrello con
la formula x=v*t
4) Il valore di x viene riportato su una retta parallela ad r e passante per il baricentro del
carrello
5) Il movimento di t su T provocherà il movimento del carrello lungo la strada
Attraverso un pulsante della prima barra dei collegamenti è possibile accedere ad una seconda
pagina, Ari1, dove viene presentato un secondo disegno, che è il primo rielaborato. In questo
disegno il carrello si muove regolato dallo stesso meccanismo del precedente, ma v è sostituito da F.
Cioè, stavolta chi muove il carrello non è la velocità ma la forza, che determina la velocità in modo
direttamente proporzionale. Si tratta del modello aristotelico di moto: “un carro non si muove se
non è spinto o trainato da qualcuno”. Nella pagina Ari2, al carrello in moto è affiancato un grafico
che riporta in ordinata la velocità ed in ascissa la forza, mostrando la relazione di proporzionalità tra
v ed F
Figura 2. Il moto secondo Aristotele
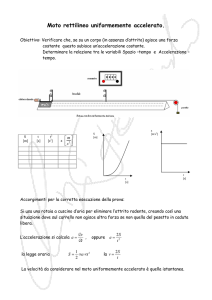
Nella terza pagina compare l’attrito. Nel disegno presente una cassa su un pavimento scabro non si
muove fin quando la forza che la spinge non supera il massimo valore che la forza di attrito
raggiunge
Figura 3. La cassa sul pavimento scabro
Le parti importanti di questo disegno sono:
1) un coefficiente di attrito statico, mis, ed un coefficiente di attrito dinamico, mid, i cui valori
vengono scelti spostando un punto, mi, su un segmento unitario
2) la cassa poggiata sul pavimento
3) il vettore F, la cui grandezza, opportunamente scalata fornisce il valore della forza applicata
4) il peso della cassa, rappresentato dall’ascissa di un punto P scelto su un segmento
orizzontale opportunamente disegnato
5) il tempo t che scorre su un vettore T, come sopra
La calcolatrice, per mezzo dell’espressione mis*P ci fornisce il valore della Fas, forza di attrito
statico, per mezzo dell’espressione mid*P ci fornisce il valore di Fad, forza di attrito dinamico. La
Fas rapprenta il valore minimo di F che mette in moto la cassa. Se F>Fas allora l’espressione F-Fad
fornisce la forza risultante, Fr, e l’espressione Fr/P/9,8 fornisce il valore dell’accelerazione, a, della
cassa. Con l’espressione 0,5*a*t^2 calcoliamo il valore di x, posizione della cassa lungo il
pavimento. Muovendo t su T, se F>Fs, osserveremo il moto uniformemente accelerato della cassa.
Se F è minore o uguale a Fas, pur muovendosi t su T, la cassa resterà ferma. L’obiettivo di questo
disegno è evidenziare l’effetto della presenza dell’attrito sul moto dei corpi.
Nella quarta pagina, Galileo1, vengono presentati due disegni, figura 4 e figura 5. Nel primo un
corpo in moto è frenato dalla forza di attrito
Figura 4. Il corpo in moto è frenato dall'attrito
In questo disegno è possibile evidenziare come l’effetto frenante dipende dal coefficiente di attrito.
In particolare è possibile evidenziare come azzerando tale coefficiente si azzera l’effetto frenante ed
il corpo non si arresta, cioè “persevera nel suo stato di moto”.
Seconda legge della dinamica
Ma allora che fa la forza?” visto che non è causa di moto. Cominciamo a trovare risposta a tale
domanda nella pagina “Newton1”, dove presentiamo un’applet che simula il moto di un carrello
soggetto ad una forza costante
Figura 5. La forza cambia la velocità
In questa applet è possibile notare come azzerando la forza la velocità del carrello rimanga costante
e come azzerando la velocità iniziale la presenza della forza metta in moto il carrello. Azzerando
invece forza e velocità iniziale evidentemente il carrello rimane fermo. La domanda successiva è:
“come la forza cambia la velocità?”
Figura 6. Dipendenza tra forza e velocità in un istante assegnato
Nella stessa applet è possibile notare come la pendenza della retta, che esprime la velocità in
funzione della forza, cambia. Ciò significa che la dipendenza tra velocità e forza dipende dal tempo.
Ma c’è una dipendenza indipendente dal tempo? Proviamo a riportare nel grafico l’accelerazione al
posto della velocità e facciamo scorrere il tempo.
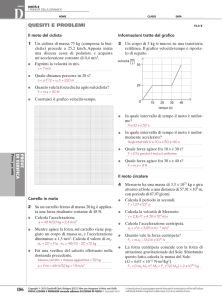
Figura 7. Dipendenza tra forza ed accelerazione
Stavolta noteremo che la pendenza della retta non varia. Noteremo anche che la retta passa per
l’origine degli assi. Potremo quindi concludere che c’è una relazione di proporzionalità diretta tra
forza ed accelerazione, tra causa ed effetto. La costante di proporzionalità tra forza ed accelerazione
è quella che si definisce “massa inerziale”.
Terza legge della dinamica
Con la prima legge impariamo quale sia il destino di un corpo non soggetto a forze; con la seconda
cosa succede ad un corpo quando su di esso agisce una forza, o un sistema di forze con risultante
non nulla; la terza ci dice che una forza non è mai sola: “ad ogni azione corrisponde una reazione
all’azione opposta”. Nella nostra relazione presentiamo due esempi di conferma di tale principio: la
forza gravitazionale e la forza elettrostatica
Figura 8. Principio di azione e reazione
Nell’applet che descrive la legge di Coulomb è possibile accendere una carica in A e scoprire cosa
succede al campo elettrico circostante. Cambiando il valore ed il segno della carica viene all’istante
aggiornata la situazione del campo intorno ad A. È anche possibile accendere due cariche, una in A
e l’altra in B evidenziando così l’interazione tra le cariche. È possibile, scoprire da quali fattori
dipende questa interazione avvicinando e allontanando la cariche e cambiandone valori e segni.
La
presentazione
descritta
in
questo
articolo
sarà
reperibile
all’indirizzo
http://www.antonioscafuro.it