carrello_orizzontale - studio a casa

Preparazione Esperienze Didattiche 2009-10
3. Carrello su guida orizzontale che urta un ostacolo – Studio a casa
Finalità
Con questo esperimento è possibile: - effettuare il confronto con la camminata regolare avanti/indietro
di uno studente; - far notare che le due s(t) (moto di allontanamento e avvicinamento) sono
sostanzialmente simili (andamenti lineari nel tempo), ma per v(t) sono qui scomparse le modulazioni
dei passi attorno all'andamento costante, tipiche del cammino umano
Questo tipo di esperimento favorisce anche la comprensione delle accelerazioni impulsive (spinte date
al carrello o blocco per fermarlo), facilitando la consapevolezza della differenza fra movimenti
familiari in cui l'attrito gioca un ruolo significativo e le situazioni astratte senza attrito illustrate nei libri
di testo; permette inoltre riflessioni, sia sulle caratteristiche e i limiti di un moto ben noto, complesso e
"sporco" che sulla semplicità del modello ideale del moto di un corpo puntiforme su traiettoria
rettilinea in assenza di attrito.
Andamenti tipici
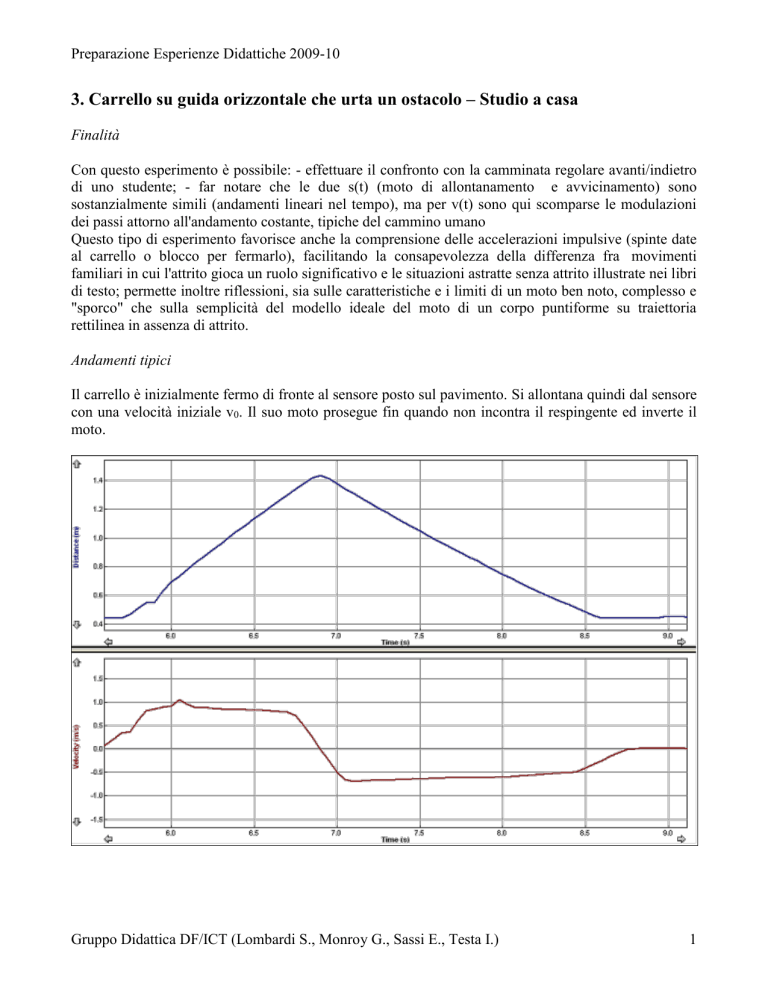
Il carrello è inizialmente fermo di fronte al sensore posto sul pavimento. Si allontana quindi dal sensore
con una velocità iniziale v0. Il suo moto prosegue fin quando non incontra il respingente ed inverte il
moto.
Gruppo Didattica DF/ICT (Lombardi S., Monroy G., Sassi E., Testa I.)
1
Preparazione Esperienze Didattiche 2009-10
Analisi dei dati
s(t): l'andamento di s(t) é ben approssimabile con una crescita lineare (pendenza positiva) nel moto di
allontanamento (a parte una piccola irregolarità avvenuta nella parte iniziale del moto) ed una
decrescita lineare (pendenza negativa) nel successivo moto di avvicinamento, dopo l'inversione di moto
(a circa 7 s). E’ evidente l’intervallo di tempo in cui il carrello è fermo, 0.5 s, quando si è fermato.
Nella fase di allontanamento la retta che meglio approssima la legge oraria ha l’espressione:
s  t   m  t  t0   q
m  0.86 ms 1 ; q  0.44 m; t0  5.7 s; t  5.7, 6.9  s
Nella fase di avvicinamento dopo l’urto contro l’ostacolo l’equazione è:
s  t   m  t  t0   q
m  0.60 ms 1 ; t0  6.9 s; q  1.42 m; t  6.9,8.6 s
La velocità del carrello è minore dopo l’urto (parzialmente anelastico). Questo andamento è evidente
dal grafico v(t).
v(t): l'andamento di v(t) mostra due tratti sostanzialmente orizzontali, congiunti da un'inversione a
gradino di durata circa 0.3 s. A causa dell’impulso iniziale trasmesso al carrello, v(t) in qualche decimo
di secondo passa da zero ad un valore positivo (circa 1 m/s) che resta circa costante fino a che la
seconda spinta rapida non inverte il moto. L’arresto, per evitare un possibile urto col sensore, é ben
evidente nel gradino smussato che porta rapidamente a zero la velocità. Le velocità medie stimate per il
moto di allontanamento e avvicinamento sono:
v all   0.88  0.06  ms 1
v avv   0.59  0.06  ms 1
Gruppo Didattica DF/ICT (Lombardi S., Monroy G., Sassi E., Testa I.)
2
Preparazione Esperienze Didattiche 2009-10
Si osserva che dopo l’urto la velocità del carrello decresce in modulo a causa dell’attrito tra le ruote e la
guida.
Gruppo Didattica DF/ICT (Lombardi S., Monroy G., Sassi E., Testa I.)
3