Happy verticality in mathematics
Stefano Babini, Ivan Graziani
Abstract "Happy verticality in mathematics" stems from the need to deploy how much anticipated in
the vertical curriculum described in the National Indications for the curriculum of the school of the
infancy and the 2012 education first cycle and pushing such verticality to the first two years of superior
education and the relative Cultural Aces and Indications.
We have thought about facing some particular conceptual knots that create difficulty in the students to all
the scholastic levels, what the geometric transformations, isometric and not, the fractions and the theory
of the probability.
Our principal purpose has been that to face such knots in different way and amusing, alternating to all
the levels the mathematical rigorousness to the imagination and the game. We are looked for so to mostly
make nice, but at the same time less loved by the greatest part of the students.
For such motive, this experience has seen involved for before the school of the infancy, with the children
of 4 and 5 years, and subsequently all the classes of the primary school, those of the secondary school of
The degree and, finally, those of the first two years of the secondary one of II degree.
Key-words Verticality, fractions, transformations, probability.
Sommario “Happy verticality in matematica” nasce dall’esigenza di mettere in campo quanto previsto
dal curricolo verticale descritto nelle Indicazioni Nazionali per il curricolo della scuola dell’infanzia e
del primo ciclo d’istruzione del 2012 e spingendo tale verticalità al primo biennio di istruzione superiore
e ai relativi Assi Culturali e Indicazioni.
Abbiamo pensato di affrontare dei particolari nodi concettuali che a tutti i livelli scolastici creano
difficoltà negli studenti, quali le trasformazioni geometriche, isometriche e non, le frazioni e la teoria
della probabilità.
Il nostro scopo principale è stato quello di affrontare tali nodi in modo diverso e divertente, alternando a
tutti i livelli la rigorosità matematica alla fantasia e al gioco.
Si è cercato così di rendere maggiormente simpatica la disciplina più bella, ma al tempo stesso meno
amata dalla maggior parte degli studenti.
Per tale motivo, questa esperienza ha visto coinvolte per prima la scuola dell’infanzia, coi bambini di 4 e
5 anni, e successivamente tutte le classi della scuola primaria, quelle della scuola secondaria di I grado
e, infine, quelle del primo biennio della secondaria di II grado.
Parole-chiave Verticalità, frazioni, trasformazioni, probabilità .
Introduzione
La verticalità e la continuità nella scuola rischiano sempre di rimanere solo sulla carta e di non
essere messe in pratica nella attività didattiche nelle varie aule.
“Happy verticality in matematica” è nato proprio per questo: per coinvolgere studenti e insegnanti
in verticale su alcuni nodi concettuali affrontati in modo divertente e soprattutto cercando di utilizzare
pochi termini, essenziali ma corretti, a tutti i livelli, fin dalla scuola dell’Infanzia, anche per evitare
misconcezioni che una volta acquisite sono difficili da smantellare.
Per questo motivo, in questo primo anno di attività, abbiamo affrontato un tema legato ai numeri,
quello delle frazioni e dei numeri razionali. Questo particolare argomento è stato scelto perché da
sempre risulta ostico per un gran numero di studenti e spesso ci si chiede come mai un argomento
affrontato fin dalla terza classe della scuola primaria non venga assimilato dagli alunni che continuano
a fare gli stessi errori fino alla scuola secondaria di secondo grado e anche oltre.
Abbiamo quindi presentato le frazioni fin dalla scuola dell’infanzia, giocando con questi numeri
particolari insieme ai bambini. Poi lo stesso argomento è stato proposto ai bambini di prima, seconda,
Experiences of Teaching with Mathematics, Sciences and Technology — Volume 1, Number 1, August 2015
5-24
Babini Stefano, Graziani Ivan
terza e quinta primaria, agli studenti di prima e seconda “media” e a quelli della seconda classe di
secondaria del liceo classico tradizionale. Sulle frazioni, purtroppo, si trovano misconcetti a tutti i
livelli scolastici. Per questo è importante chiarirli fornendo, soprattutto ai bambini, poche informazioni
semplici, ma corrette e rigorose.
Destinatari e tempi
L’attività è stata svolta durante l’anno scolastico 2014/2015 presso le scuole dell’Infanzia, Primaria
e Secondaria di primo grado dell’Istituto Comprensivo di Santa Sofia (FC) di Santa Sofia e presso la
quinta ginnasio del Liceo Classico “Rambaldi – Valeriani – A. Da Imola” di Imola (BO).
Gli incontri nelle classi della scuola dell’Infanzia e in quelle della Primaria sono stati due di due
ore ciascuna insieme all’insegnante della classe. Nelle Scuole secondarie di I e II grado sono state
effettuate cinque lezioni di due ore ciascuna.
Attività e sperimentazione
Le frazioni
L’introduzione delle frazioni ai bambini di 4 e 5 anni è avvenuta attraverso la piegatura della carta
e la simulazione di una spartizione di torta di compleanno. I bambini hanno suddiviso prima a metà,
poi in 4 parti, in 8 parti e in 16 parti, partendo da un foglio rettangolare dato a ciascuno di loro. Siamo
poi passati all’introduzione di alcuni termini specifici a loro sconosciuti come “un mezzo” (non di
trasporto …) , poi un quarto, un ottavo e un sedicesimo. Siamo poi passati a osservare diverse quantità
partendo dalle frazioni unitarie e all’osservazione diretta, sempre dalle fette di torta, dell’equivalenza
di frazioni semplici come 1 con 2 , 4 e 8 . Per questo livello di scuola ci sembra già abbastanza.
2
4
8
16
L’approccio con i bambini della prima classe della scuola Primaria è stato differente ed è partito
dalla probabilità e dalla sua rappresentazione in alcuni casi, come ad esempio nel lancio di una moneta
o di un dado a sei facce. Anche in questo caso abbiamo prima incontrato le frazioni unitarie, come la
probabilità che esca una delle due facce della moneta, 1 , e come la probabilità che esca un
2
determinato numero di un dado,
1,
6
per poi passare ad alcune frazioni equivalenti, come 3 individuata
6
come probabilità di ottenere un numero pari con il dado, che rappresenta anche la metà dei casi
favorevoli e quindi 1 . Abbiamo incontrato altre frazioni utilizzando un sacchetto con 10 caramelle,
2
prima tutte nere, poi sostituendo gradualmente alcune caramelle nere con altrettante verdi, potendo
così ragionare anche sulle frazioni complementari.
Anche con i bambini della seconda classe primaria siamo partiti dalla probabilità e abbiamo
costruito frazioni unitarie e equivalenti, come rappresentazione di casi probabili: uno su 2 (moneta
testa o croce) 1 , uno su 6 (ottenere 2 col dado) 1 .
2
6
Abbiamo chiesto ai bambini se sapevano cos’era un numero pari e un numero dispari, perché di
solito questo argomento si tratta solo in seconda. Visto che quasi tutti conoscevano già la differenza
tra numero pari e numero dispari, compresi tra uno e sei, abbiamo chiesto: “Qual è la probabilità,
lanciando un dado di ottenere un numero pari?”. Diversi bambini hanno subito alzato la mano e
risposto: “3 su 6” e una anche “ 3 ”. Un bambino ha poi detto “ma è la metà dei casi e allora è anche 1
6
2
” e una bambina ha aggiunto “il 50%”, introducendo così un’altra rappresentazione semiotica dello
stesso numero.
Anche in questa classe abbiamo utilizzato il sacchetto con le caramelle e la piegatura del foglio di
carta formato A4 in 16 parti come avevamo già visto nella scuola dell’infanzia. Ci siamo soffermati
sulla necessità di piegare con una certa precisione la carta per ottenere parti uguali.
6
EDiMaST — Volume 1, Number 1, May-August 2015
Happy verticality in mathematics
È importante però definire insieme ai bambini in che cosa vogliamo che siano uguali le parti.
Possiamo fare un esempio con un foglio di carta formato A4 e chiedere agli alunni di dividere tale
foglio a metà. Otterremo tre tipologie di piegatura: due secondo gli assi del rettangolo e una secondo la
diagonale come:
Abbiamo chiesto allora: “Tutte queste parti che avete ottenuto rappresentano la metà del foglio?”.
Una bambina ha detto: “Ma non sono uguali!”. Qui si può dire che due o più parti possono essere
uguali per forma, per dimensioni, per numero, per peso, ecc… è importante quando si parla di uguale
specificare bene cosa si intende con questo termine utilizzato spesso in modo non corretto. Per tale
ragione anche l’uso di torte o pizze per rappresentare le frazioni non è il modo migliore, secondo noi,
per introdurre questo concetto.
Il passaggio alle frazioni unitarie e a quelle complementari, attraverso l’osservazione del foglio
piegato, è stato più immediato se prima erano state esaminate le frazioni con moneta, dado e
caramelle.
Nella classe terza della primaria, classe in cui solitamente si introducono le frazioni siamo partiti
con la piegatura di un foglio formato A4. Abbiamo prima diviso il foglio con una piega in due parti
uguali e poi, con una seconda piega, in ulteriori due parti uguali. Quindi abbiamo riaperto il foglio e
abbiamo osservato che le parti in cui era stato diviso erano 4. Abbiamo richiuso il foglio nella
condizione in cui era dopo la seconda piega e lo abbiamo piegato di nuovo per due volte di seguito
sempre in parti uguali. Riaprendo poi il foglio si è notato che ora le parti erano diventate 16.
Abbiamo quindi scritto alla lavagna la relazione esistente tra numero di pieghe e parti:
1 piega – 2 parti; 2 pieghe – 4 parti; 3 pieghe – 8 parti; 4 pieghe – 16 parti. Una bambina ha notato
“Raddoppiano sempre”.
Allora ho chiesto quante parti sarebbero venute fuori piegando per la quinta volta il foglio e la
risposta è stata in coro “32 parti”. Quindi era intuitivo che ogni volta le parti raddoppiassero. Qui si
poteva introdurre il concetto di potenza, ma era troppo presto perché le incontreranno solo in quarta o
in quinta. Però abbiamo fatto notare che prima era solo 2, poi 2 x 2, poi 2 x 2 x2 e sono andati avanti
loro fino a 2 x 2 x 2 x 2 x 2 x 2 = 64.
Abbiamo quindi ripassato con il pennarello le pieghe che si vedevano riaprendo il foglio e abbiamo
scritto le frazioni unitarie aggiungendo anche 1 , facendo una piega sola sul rettangolino di 1 .
32
16
Anche in questo caso abbiamo potuto osservare le frazioni equivalenti di
1
2
e una bambina ha
notato che “il numero sopra e il numero sotto raddoppiavano sempre” e quindi siamo arrivati alle
frazioni equivalenti e anche alla proprietà invariantiva delle frazioni.
In un altro incontro siamo ritornati alle frazioni partendo da un Tangram, spiegando che il tan è il
triangolo più piccolo. E’ stato chiesto qual era secondo loro la parte rappresentata da tale triangolo.
Dopo alcuni tentativi un po’ sbagliati, ho suggerito di vedere quante volte il triangolo stava nel
quadrato piccolo e nelle altre figure più grandi. Una bambina ha risposto che ci stava “16 volte nel
tangram” e quindi che era 1 . Allora ho chiesto quante volte ci stavano le altre figure e varie mani si
16
sono alzate per dire che il quadrato, il parallelogramma e il triangolo medio ci stavano 8 volte equindi
erano 1 e, di conseguenza, i due triangoli più grandi erano 1 .
8
4
Ho chiesto “proviamo a sommare queste parti perché insieme devono fare un intero cioè 1”. Sono
rimasti un po’ perplessi, ma abbiamo scritto alla lavagna tutte le frazioni del tangram sommate tra di
loro.
1 1 1 1 1 1
1
+ + + + + +
=
4 4 8 8 8 16 16
EDiMaST — Volume 1, Number 1, May-August 2015
7
Babini Stefano, Graziani Ivan
Ho fatto notare, utilizzando le varie parti ottenute col foglio piegato precedentemente, che si riescono
a sommare tra loro solo le frazioni che hanno il denominatore uguale e quindi 1 + 1 = 2 poi
4 4 4
1 1 1 3 e 1
1
2 perciò la somma ora era 2 3 2
+ + =
+
=
+ +
= 1 . Abbiamo notato che i denominatori
8 8 8 8
16 16 16
4 8 16
4 e 8 potevano diventare 16 con le frazioni equivalenti viste la volta precedente, mentre i numeri più
grandi in questo caso non potevano diventare come quelli più piccoli. Per tale motivo abbiamo scritto
sotto 2 8 + 3 6 + 2 = 16 che è l’intero e quindi 1.
4 16 8 16 16
16
Per continuare a parlare di somme di frazioni abbiamo utilizzato una tabella costruita insieme ai
ragazzi della prima secondaria di I grado con word e suddivisa prima in 2 poi in 3 in 4 ecc fino a 20
parti e abbiamo scritto e colorato le varie unità frazionarie in modo da evidenziare anche le parti
equivalenti (fig.1).
1
1/2
1/3
1/4
1/5
1/6
1/7
1/8
1/9
1/10
1/12
1/15
1/16
1/18
1/20
Fig. 1 – Tabella delle frazioni
In questo modo si evidenziano che frazioni come 1 e 1 si trovavano anche nella riga di 1 e che
2 3
6
1
1
5
1
1
quindi si vede che la loro somma
e
lo troviamo nella riga del 12 e quindi si nota
+ =
+
2 3 6
3 4
ancora che la loro somma 1 + 1 = 7 e cosi via. Nella classe quinta della scuola primaria abbiamo
3 4 12
ripassato le frazioni che gli alunni avevano già incontrato a partire dalla classe terza: siamo partiti in
questo caso con la piegatura di un foglio formato A4, suddividendolo prima a metà (alcuni alunni
hanno piegato il foglio secondo l’asse più lungo e altri secondo quello più corto) poi in 4 parti. Poi
8
EDiMaST — Volume 1, Number 1, May-August 2015
Happy verticality in mathematics
abbiamo piegato nuovamente il foglio come avevamo già fatto con gli alunni della terza classe fino ad
arrivare alla suddivisione in 16 parti.
Anche qui ho scritto alla lavagna la relazione esistente tra il numero di pieghe effettuate e le parti
ottenute.
Ho poi chiesto ai bambini se osservavano qualche particolarità per quei numeri e due alunne hanno
subito notato che erano “potenze”. Io ho chiesto “quali potenze?” E una ha risposto “di 2” e quindi
“21= 2, 22= 4, 23= 8 e 24 = 16”. Ho chiesto allora se si poteva intuire quale fosse il numero
successivo. Un alunno ha prontamente risposto “32 perché è 25 e poi dopo c’è 26 che è 64 e così via”.
Abbiamo segnato con pennarelli di vario colore le varie pieghe che si erano formate e abbiamo
scritto nei riquadri formati le varie frazioni unitarie.
Si sono potute poi osservare, come fatto precedentemente, le varie frazioni equivalenti.
Ho fatto notare che queste frazioni insieme dovevano dare l’intero, cioè il foglio A4 che avevamo
piegato. Visto che qualcuno sembrava un po’ scettico, lo abbiamo verificato attraverso la somma delle
singole parti:
1 1 1 1
2
+ + + +
= 1.
2 4 8 16 32
Osservando le varie parti ottenute piegano il foglio si evidenzia che le somme si possono fare solo se
le frazioni hanno denominatori uguali. Perciò i denominatori più piccoli dovevano diventare come
quelli maggiori attraverso il procedimento delle frazioni equivalenti già visto prima. Quindi il
denominatore che tutte dovevano avere era 32.
1 16 1 8 1 4 1 2 2 32
=
=1
+ + + +
2 32 4 32 8 32 16 32 32 32
Anche in questa classe come già in terza, abbiamo poi fatto l’attività partendo dal tangram, che gli
alunni avevano già incontrato con le loro docenti.
Questo secondo incontro è stato interamente dedicato a “giocare a scopa con le frazioni”.
Abbiamo utilizzato il mazzo di carte particolare con la faccia delle figure e dei numeri sostituite da
frazioni con denominatori 3, 4, 5 e 6. I numeratori sono invece tali da non formare frazioni che
diventano numeri interi (quindi non 3 , 8 o 8 ).
3 4 2
Il gioco inizia con la scelta di chi deve dare le carte: tale ruolo spetta a chi sceglie la carta più alta
(si ripassa quindi il confronto tra le frazioni). Si parte poi dando 3 carte ai giocatori e mettendo 4 carte
in tavola (come a scopa): si possono prendere dal tavolo solo le frazioni che con la propria carta diano
numeri interi. Ad esempio: 1 + 3 = 4 equivale a 2 punti
2
2
2
2 7 9 equivale a 3 punti e così via (qui,
+ =
3 3 3
oltre alle somme di frazioni con denominatori uguali, si ripassano i multipli e i divisori).
I punti ottenuti vanno segnati volta per volta. Se prendendo una carta dal tavolo non ne rimangono
altre si raddoppia il punteggio per la scopa e si somma a quello già raggiunto.
Al termine l’ultimo che effettua l’ultima presa, prende anche le altre carte sul tavolo e, per
calcolare quanto vale il punteggio di tali carte, si deve fare la loro somma (in questo caso la somma è
tra frazioni con denominatori diversi e quindi abbiamo ricordato il procedimento seguito nell’incontro
precedente).
Ai bambini è piaciuto molto questo gioco che esprime al meglio il concetto di divertirsi con la
matematica.
Nella prima classe della scuola secondaria di I grado abbiamo introdotto le frazioni nello stesso
modo della primaria, cioè attraverso la piegatura di un foglio di formato A4, ma anche di un foglio
quadrato, e con il tangram.
Dopo aver in questo modo ripreso alcuni aspetti che gli studenti avevano affrontato nella scuola
primaria, abbiamo cercato di realizzare una tabella che riassumesse in forma grafica alcuni concetti
visti, come le frazioni equivalenti, la somma di frazioni, anche con l’intento di realizzare uno
strumento da presentare agli studenti della scuola primaria. I ragazzi hanno così creato una tabella
(quella mostrata nella quinta primaria) utilizzando un programma di scrittura e lasciando la prima riga
EDiMaST — Volume 1, Number 1, May-August 2015
9
Babini Stefano, Graziani Ivan
della tabella intera, la seconda divisa in 2, la terza divisa in 3 e così via fino all’ultima divisa in 20. La
tabella del programma di scrittura tramite la possibilità di dividere ogni riga in un numero stabilito di
colonne ha permesso di realizzare delle strisce con le frazioni che interessavano.
I ragazzi hanno evidenziato frazioni con i colori utilizzando lo stesso per le frazioni equivalenti, in
modo da ottenere un impatto visivo immediato.
Con le colorazioni diverse scelte è possibile soffermarsi anche su alcune somme tra frazioni come
1
o 1+1 = 3, 1+1 = 7 , 1+1= 8 , 1+1= 9 ,
ad esempio 1 + 1 = 5 che troviamo nella riga di
6
2 3 6
2 4 4 3 4 12 3
1 1 5 , ecc. Inoltre, “scendendo” lungo la tabella, si notano alcune regolarità.
+ =
4 6 12
5
15
4
5
20
Nelle lezioni successive abbiamo realizzato dei piccoli cartelloni in formati A3, lavorando a piccoli
gruppi. Tali cartelloni sono stati poi assemblati in un unico cartellone grande che è stato presentato dai
ragazzi della prima secondaria di I grado agli alunni delle classi quinte della scuola Primaria.
Fig. 2 – Cartellone realizzato dai ragazzi delle classi 1a e 2a della Secondaria di I grado.
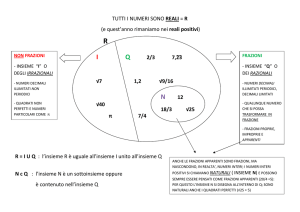
I cartelloni realizzati sono stati: frazioni dal tutto alla parte, dalla parte al tutto, come quoziente,
come operatore, come numero, come punti su una retta orientata, come collegamenti, come probabilità
e frazioni e musica (fig.2).
La parte relativa alle frazioni come rapporto, è stata aggiunta dai ragazzi della classe seconda che
in quel periodo stavano svolgendo le attività sulle proporzioni. Questa non è stata illustrata ai bambini
di quinta primaria, ma è stata aggiunta al cartellone che ci accompagnerà anche nella classe seconda.
Anche in questa classe abbiamo poi giocato a scopa con le frazioni con le stesse modalità elencate
per la quinta primaria.
10
EDiMaST — Volume 1, Number 1, May-August 2015
Happy verticality in mathematics
Nella seconda classe delle “medie” siamo passati alle frazioni come rapporti e quindi alle
proporzioni. Abbiamo ripassato le frazioni come rapporto tra due numeri e quindi anche il concetto di
grandezze commensurabili e non commensurabili.
Siamo passati alle proporzioni come uguaglianza tra due rapporti e quindi tra due frazioni, siamo
quindi ritornati alle frazioni equivalenti già note ai ragazzi.
Abbiamo affrontato le varie proprietà delle proporzioni partendo da quella fondamentale per poi
arrivare alle altre.
Successivamente abbiamo considerato alcuni problemi risolvibili con le proporzioni in vari campi
e notato quanto le proporzioni e la proporzionalità intervengano in tanti processi in ambito chimico,
fisico e anche sociale. La ricerca delle varie relazioni tra le proporzioni, la conseguente estensione
dell’ambito matematico ad altri ambiti scientifici (chimica, fisica, tecnologia) e sociali (ricette
alimentari, sconti, ecc…) ha portato alla realizzazione di una mappa concettuale che è stata
rappresentata su un cartellone (vedi Fig.3), realizzato in collaborazione con l’insegnante di Tecnologia
e nelle ore di Scienze durante tutto il secondo quadrimestre. Questo ci ha consentito di realizzare
numerosi collegamenti, anche con concetti come quello di rapporto aureo o con il teorema di Talete,
solitamente non affrontati in questo segmento di scuola, ma che, a nostro avviso, se affrontati insieme
a similitudine e proporzioni, sono più facilmente comprensibili dagli studenti già a partire dal secondo
quadrimestre della seconda “media”.
Fig. 3 – Cartellone realizzato dai ragazzi della classe 2a della Secondaria di primo grado.
Nella scuola secondaria di secondo grado, in una quinta ginnasio del liceo classico e in una
seconda di scienze umane, abbiamo affrontato il problema del passaggio dalle frazioni conosciute alle
frazioni algebriche, osservando in particolare le analogie esistenti.
EDiMaST — Volume 1, Number 1, May-August 2015
11
Babini Stefano, Graziani Ivan
Abbiamo innanzitutto introdotto le frazioni algebriche come estensione di quelle numeriche.
La semplificazione delle frazioni e l’applicazione della proprietà invariantiva per ridurle ai
minimi termini ci ha portato a confrontare le frazioni algebriche con quelle numeriche. Per quanto
riguarda le frazioni algebriche vi è la complicazione di dover fattorizzare e semplificare polinomi
anziché numeri. Abbiamo realizzato quindi una tabella (tab.1) di confronto per visualizzare meglio le
analogie.
Tab. 1 – Confronto tra frazioni numeriche e algebriche.
Frazioni Numeriche
Frazioni di partenza
25
10
Fattorizzazione
Semplificazione
5
2
Frazioni Algebriche
−2 +1
−1
−1
+1
−1
−1
+1
Naturalmente nella semplificazione va detto che x – 1 deve essere diverso da 0 per non annullare il
denominatore e che quindi si deve porre x ≠ 1.
Si arriva così attraverso ragionamento e analogie alla definizione di frazione algebrica e alla
definizione del campo di esistenza considerando il fatto che il denominatore di una frazione non può
essere 0.
Successivamente abbiamo introdotto l’addizione e la sottrazione di frazioni algebriche ancora come
estensione di tali operazioni con le frazioni numeriche.
Si ripete così come si ottiene il denominatore comune e come si comporta il numeratore una volta
trovato il minimo comune multiplo fra i denominatori di due frazioni da sommare algebricamente
dopo aver provveduto a fattorizzare i denominatori. Si osserva, in questo modo, che il procedimento è
del tutto analogo, ma adesso con dei polinomi.
Si procede con l’introduzione di moltiplicazione, divisione e potenza sempre seguendo un
parallelismo con le frazioni numeriche.
Si conclude passando alla risoluzione di espressioni contenenti frazioni algebriche, ancora
nuovamente come estensione delle espressioni con le frazioni viste alle affrontate nelle scuole
“medie”.
Le trasformazioni geometriche
Il secondo nodo concettuale che abbiamo affrontato in verticale è stato quello delle trasformazioni
geometriche, anche in questo caso partendo dalla scuola dell’infanzia.
Innanzitutto abbiamo introdotto la geometria: come “misurazione della terra”, poi, verificato che i
bambini conoscevano alcune forme acquisite come blocchi logici, siamo passati al riconoscimento di
alcune figure geometriche standard, mostrate anche in posizioni non “convenzionali”.
Siamo poi passati allo spostamento di tali figure, ma anche di oggetti e di persone (insegnanti e
alunni) su un piano, rappresentato da una scacchiera realizzata con delle strisce adesive sul pavimento.
Abbiamo chiesto ai bambini se le figure, spostandole, si modificavano. Hanno risposto tutti “no”.
Abbiamo colto l'occasione per precisare che lo spostamento di figure su un piano che non ne provochi
una modifica viene definita traslazione. Abbiamo poi fatto spostare sulla scacchiera le varie figure
fornendo dei comandi semplici.
Poi siamo passati alle simmetrie e in particolare alla simmetria assiale: attraverso un asse che
divideva a metà la scacchiera sul pavimento, abbiamo posizionato prima dei poligoni e poi alcuni
alunni in modo simmetrico rispetto a tale asse. Per mostrare cosa accadeva abbiamo anche simulato
con una scenetta una persona davanti allo specchio per mostrare che le figure, come anche le persone,
12
EDiMaST — Volume 1, Number 1, May-August 2015
Happy verticality in mathematics
con la simmetria assiale cambiano: si visualizza bene ruotando i due alunni che hanno simulato lo
specchio. Si dimostra così che per riportare le figure alla situazione iniziale occorre sollevarle dal
piano e ruotarle.
Abbiamo poi fatto il gioco del Twister simmetrico: i bambini dovevano riprodurre
simmetricamente quanto fatto dai compagni dall’altra parte dell’asse.
Nell’incontro successivo abbiamo ricercato insieme ai bambini la simmetria assiale nei poligoni,
nelle lettere e nei numeri: utilizzando figure, lettere e numeri ritagliati su carta è stato chiesto ai
bambini di fare delle pieghe in modo da dividere gli oggetti in modo uguale (sovrapponibile).
Nella classe prima della scuola primaria abbiamo effettuato le stesse attività della scuola
dell’infanzia con l’aggiunta della ricerca di simmetrie assiali, oltre che nelle lettere e nei numeri anche
in natura, come nella forma della farfalla. I bambini hanno poi realizzato delle forme con i colori a
tempera e poi piegando il foglio realizzato i simmetrici per impronta-stampa.
Anche nella classe seconda della scuola primaria abbiamo ripetuto le cose precedenti viste per
traslazione e simmetria centrale, ma abbiamo introdotto anche la particolarità del triangolo rettangolo,
che rende più visibile il cambiamento della figura rispetto ai poligoni regolari che i bambini
utilizzavano come blocchi.
Abbiamo mostrato che i due triangoli rettangoli ottenuti suddividendo un foglio A4 in due parti
lungo la diagonale, anche se hanno i lati uguali, non sono sovrapponibili. Abbiamo allora chiesto ai
bambini cosa bisognava fare per rendere uguali e sovrapponibili i due triangoli. Un bambino ha detto
“uno lo devi girare”).
Abbiamo quindi fatto osservare che la natura di una figura è indipendente dalla posizione: “Andrea, se
lo giro o se si alza o si siede, rimane sempre Andrea”. Abbiamo quindi mostrato la stessa figura vista
da diverse angolazioni e poi abbiamo ripetuto lo stesso esperimento con un alunno. In questo caso il
quadrato in posizione non convenzionale non viene subito riconosciuto. Allora abbiamo suggerito: “se
ci incliniamo possiamo vedere che si tratta sempre della stessa figura” e i bambini, vedendo, hanno
creduto.
Piegando poi un foglio A4 a metà secondo i due assi, in successione, abbiamo fatto notare che le
due linee si incontrano in un punto. Passando poi al foglio quadrato abbiamo notato che questo si può
piegare in quattro modi diversi, ma che tutte le linee formate si incontrano in un punto. Un’alunna dice
“nel centro” e quindi abbiamo trovato il centro di simmetria.
Fig. 4 – Simmetrie assiali
EDiMaST — Volume 1, Number 1, May-August 2015
13
Babini Stefano, Graziani Ivan
Esistono numeri e lettere con centro di simmetria? Subito viene individuato lo zero 0 tra i numeri e
la O tra le lettere. Posizionando i fogli con le lettere alla finestra e osservandole in controluce abbiamo
visto che alcune lettere come A, H, I, M, O, T, U, V, X e Y non cambiavano e che I, H, O e X non
cambiavano nemmeno se venivano ribaltate. Abbiamo chiesto: “E questo cosa significa?” Una
bambina ha risposto: “Che le seconde hanno due assi e anche un centro”. Brava!
Poi siamo passati alle quarte della scuola primaria e qui le trasformazioni le abbiamo osservate in
laboratorio con il software GeoGebra.
I bambini non avevano mai utilizzato il software, quindi abbiamo inizialmente introdotto GeoGebra
e i suoi comandi per rappresentare punti, segmenti e poligoni.
Sì è poi proseguito richiamando le trasformazioni geometriche, che gli alunni avevano già
affrontato con le loro insegnanti nei mesi precedenti, e abbiamo provato a realizzare, in particolare,
quelle relative alle simmetrie, assiale e centrale, con l’uso del software.
Siamo partiti con la simmetria assiale: abbiamo potuto osservare, in particolare con il triangolo
rettangolo che la simmetria assiale non lascia inalterata la figura, ma la modifica. Un bambino ha
notato che “una va in senso orario e l’altra in senso antiorario”. Abbiamo richiamato l’analogia con la
nostra immagine riflessa da uno specchio.
Abbiamo quindi ricordato che la simmetria assiale è l’unica trasformazione isometrica che si
facendo uscire la figura dal piano per effettuare un ribaltamento.
Abbiamo poi provato a vedere cosa succedeva con la simmetria centrale.
Fig. 5 – Simmetrie centrali
In questo caso abbiamo potuto osservare che, a differenza di quello precedente,le figure
rimanevano uguali e sovrapponibili.
Nel successivo incontro abbiamo ripreso a utilizzare GeoGebra (vedi Fig.5), che nel frattempo
qualche alunno aveva già scaricato e usato a casa, e anche le insegnanti avevano ripreso in classe nei
giorni successivi al primo incontro.
Abbiamo quindi provato ad osservare che cosa succedeva con la traslazione. Gli alunni avevano già
avuto esperienza con questa trasformazione nei giorni precedenti e ricordavano che per questa
trasformazione era necessario introdurre un vettore. Abbiamo perciò richiamato le caratteristiche del
vettore e, in particolare, quelle del modulo, del verso e della direzione.
14
EDiMaST — Volume 1, Number 1, May-August 2015
Happy verticality in mathematics
Si è proseguito quindi con l’introduzione dei comandi di GeoGebra per realizzare la traslazione.
Prima il comando per definire il vettore e poi quello per effettuare la traslazione.
Abbiamo provato a utilizzare tre vettori che differivano per direzione e verso; questo ci ha
permesso di osservare che anche, come già verificato per la simmetria centrale, le figure traslate non
venivano modificate da questa trasformazione (vedi Fig.6).
L’attività, svolta interamente nell’aula di informatica, ci ha permesso di introdurre l’uso del
software di geometria dinamica fin da questa classe della primaria, questo contribuendo al
raggiungimento del traguardo di competenze europee legato alle competenze digitali.
Ci ha inoltre permesso di visualizzare alcuni concetti, come quello delle trasformazioni
geometriche, in una veste diversa dalla solita utilizzata per la scuola primaria, basata in genere sul
lavoro nel quaderno, avendo anche la possibilità di modificare dinamicamente la posizione di punti e
poligoni e di osservare che conseguentemente si muovevano gli elementi a loro legati dalle relazioni
impostate.
Fig. 6 – Traslazioni
Siamo poi passati agli alunni della classe seconda della secondaria di primo grado.
Abbiamo introdotto le trasformazioni geometriche iniziando da quelle isometriche, che hanno la
proprietà di lasciare inalterate le misure degli oggetti.
Abbiamo utilizzato il piano cartesiano e spostato su di esso, con l’aiuto di GeoGebra, punti, segmenti e
poligoni, le stesse operazioni venivano effettuate dagli alunni anche sul quaderno. Abbiamo simulato
anche sulla cattedra e sul pavimento lo spostamento di oggetti, come astucci, penne e zaini. Abbiamo
chiesto di osservare se dopo lo spostamento le figure avessero subito qualche modifica. La risposta è
stata univoca: “No”. Abbiamo quindi informato gli studenti che questa trasformazione in geometria si
chiama traslazione e che viene realizzata secondo un vettore, già conosciuto in fisica e in tecnologia
per la rappresentazione delle forze, ricordando che è composto da quattro elementi: il punto di
applicazione (che coincide con il punto in cui si trova l’oggetto da spostare), la direzione
(rappresentata dalla retta lungo la quale si muove l’oggetto) il verso (indicato dalla punta della freccia)
e il modulo (rappresentato dalla lunghezza della freccia, indica la misura dello spostamento).
Abbiamo quindi affrontato le simmetrie: prima quella assiale, poi quella centrale.
EDiMaST — Volume 1, Number 1, May-August 2015
15
Babini Stefano, Graziani Ivan
L'attività è stata svolta sul quaderno utilizzando come assi di simmetria quelli del piano cartesiano.
Ad esempio abbiamo spostato le figure dal primo quadrante al secondo assumendo l’asse y come asse
di simmetria.
Abbiamo osservato come cambiavano le coordinate dei punti dopo questa operazione. I ragazzi
hanno subito notato che cambia solo il segno della coordinata relativa all’asse di simmetria.
Spostando simmetricamente un rettangolo, un quadrato o altri poligoni regolari non si notano
cambiamenti nelle figure. Applicando le stesse trasformazioni al triangolo rettangolo si nota che il suo
simmetrico non è sovrapponibile. “È come uno specchio” osserva una ragazza, “È come se fosse
ribaltato” aggiunge un ragazzo. “Avete ragione entrambi. In questo caso diventa evidente che, con
questo tipo di simmetria, gli oggetti cambiano. Escono dal piano e, come hai detto tu, si ribaltano”.
“Accadrà la stessa cosa anche con la simmetria centrale, nella quale il riferimento è dato da un
punto?” Tale punto viene chiamato centro di simmetria.
Abbiamo provato prima sul quaderno e poi utilizzato la griglia di GeoGebra, escludendo questa
volta gli assi cartesiani. Dopo aver applicato la trasformazione a punti e segmenti siamo passati ai
poligoni, partendo però questa volta proprio dal triangolo rettangolo. Gli studenti hanno subito notato
che “questa volta la figura non cambia” e si comporta “come se ruotasse”. Quindi ho chiesto “allora
in questo caso esce dal piano?”. La risposta è stata immediata: “No”.
“E riguardo all’asse cartesiano come cambiano le coordinate?”. Hanno subito risposto
“Cambiamo segno tutte e due”.
Siamo poi passati alla ricerca di assi e centri di simmetria nei poligoni conosciuti. Ne abbiamo
analizzati alcuni in classe utilizzando fogli di carta, poi siamo andati in laboratorio per lavorare con
GeoGebra. I ragazzi hanno realizzato le varie figure, triangoli, quadrilateri, alcuni poligoni regolari,
arrivando fino al cerchio.
Fig. 7 – Omotetia diretta
È stato poi chiesto ai ragazzi di trovare immagini (in natura, in oggetti o in monumenti, ecc…) che
presentassero traslazioni, o simmetrie assiali o centrali.
16
EDiMaST — Volume 1, Number 1, May-August 2015
Happy verticality in mathematics
Siamo poi passati alle trasformazioni non isometriche, cioè quelle che lasciano inalterate solo le
misure degli angoli, abbiamo parlato dell’omotetia diretta e inversa. Anche in questo caso è stato utile
avvalersi del programma GeoGebra. Con questa trasformazione si spostano le figure, ma queste
possono aumentare di dimensione oppure ridursi. “Come con le fotocopie” ha suggerito una ragazza.
“Anche in questo caso abbiamo un punto di riferimento che si chiama centro di omotetia. Si ottiene
l’effetto del proiettore del cinema o della nostra LIM. L’immagine inizialmente è piccola e poi diventa
sempre più grande man mano che ci allontaniamo”.
I ragazzi hanno osservato che le distanze dei punti della figura iniziale dal centro di omotetia e
quelli dei punti della trasformata, messe in rapporto, danno un valore costante, detto costante o
rapporto di omotetia, oppure caratteristica e viene indicato con k. Il numeratore di tale rapporto è
costituito dalla distanza dal centro di un punto della figura trasformata, il denominatore dalla distanza
dal centro del punto corrispondente nella figura di partenza. Abbiamo indicato con le lettere A, B e C i
vertici di un triangolo e con A’, B’ e C’ quelli del triangolo trasformato con omotetia in base al centro
di omotetia O (vedi Fig.7).
Abbiamo osservato che per ogni coppia di vertici, il rapporto della distanza dal centro di omotetia
ha la seguente proprietà:
OA ' OB ' OC ' 2
=
=
=
OA OB OC 1
si può notare che, nel rapporto della prima trasformazione da ABC in A’B’C’, il numeratore è
maggiore del denominatore e che la figura è ingrandita.
Per il triangolo A’’B’’C’’ i rapporti sono OA '' = OB '' = OC '' = 1 .
OA
OB
OC
2
In questo caso N < D e la figura è ridotta.
Fig. 8 – Omotetia inversa
EDiMaST — Volume 1, Number 1, May-August 2015
17
Babini Stefano, Graziani Ivan
Anche in questo caso pur trattandosi di un’omotetia inversa, cioè con spostamento dalla parte
opposta rispetto al centro di omotetia,
omotetia i rapporti risultano gli stessi del primo caso visto:
OA ' OB ' OC ' 2
=
=
=
OA OB OC 1
Quindi per valori di k > 1 (cioè se N > D) si ha un ingrandimento delle figura iniziale, mentre per
k < 1 (cioè se N < D) si ha una riduzione della figura di partenza.
Abbiamo osservato, sempre con GeoGebra,
Geo
che nelle omotetie le figure cambiano, ma rimangono
uguali le ampiezze degli angoli (misurati con l’apposito comando) e eventuali parallelismi tra i lati
delle figure, come abbiamo potuto notare con quadrato e rettangolo (vedi Fig.8).
In pratica le figure non sono più isometriche, ma diventano simili.
Fig. 9 – Simmetria centrale di punti sul piano cartesiano.
L’omotetia offre quindi lo spunto per parlare di similitudine, per riprendere in mano le frazioni e
per addentrarsi nel mondo dei rapporti e delle proporzioni.
Inoltre porterà ad affrontare, in geometria,
geometria altri tre teoremi dopo quello di Pitagora: i due teoremi di
Euclide e il teorema di Talete.
In una quinta ginnasio del liceo classico e in una seconda di scienze umane abbiamo affrontato la
simmetria centrale: nella prima lezione abbiamo introdotto
in
il concetto di simmetrico dei punti A, B, C
rispetto all’origine O prima sul foglio di carta e poi con GeoGebra (vedi Fig.9).
Abbiamo chiesto ai ragazzi cosa potevano osservare relativamente alle coordinate dei tre punti e
dei loro simmetrici.
I ragazzi
agazzi hanno osservato che:
1 – lee coordinate di A’, B’, C’ sono quelle di A, B, C cambiate di segno (vedi Fig. 10)
2 – i punti medi dei segmenti AA’, BB’, CC’ coincidono tutti con O.
O
18
EDiMaST — Volume 1, Number 1, May-August 2015
Happy verticality in mathematics
Fig. 10 – Simmetria centrale di segmenti sul piano cartesiano.
Abbiamo quindi potuto dedurre che:
lee equazioni della simmetria di centro O sono:
−
−
pervenendo poi alla definizione generale di simmetria rispetto all’origine.
all’origine
Il passo successivo è stato quello di estendere a un qualunque punto P del piano quanto già appreso in
questa prima lezione in modo da pervenire alla
al definizione generale di simmetria (sviluppata poi nella
seconda lezione).
Nelle lezioni seguenti si sono poi sviluppate tutte le trasformazioni nel piano cartesiano utilizzando
lo stesso metodo intuitivo.
La probabilità
Un altro tema affrontato nella scuola dell’infanzia è stato quello di probabilità, termine per loro
ancora non troppo chiaro.
Siamo partiti dal concetto di impossibile chiedendo ai bambini di fare degli esempi su cosa
intendessero per impossibile. Gli esempi proposti dai bambini non rappresentavano
appresentavano eventi impossibili,
ma solo poco probabili, quindi ci siamo soffermati sulla differenza tra questi due termini.
Abbiamo visualizzato in modo concreto dei casi impossibili, certi e probabili attraverso un
sacchetto con 10 caramelle inizialmente
inizialme
tutte nere, procedendo poi con la sostituzione di alcune
caramelle nere con altrettante verdi. La richiesta iniziale è stata, quando il sacchetto conteneva solo
caramelle nere: “È possibile estrarre una caramella verde?”.
verde?”. I bambini hanno detto subito di no. Poi
togliendo un a caramella nera dal sacchetto e sostituendola con una verde abbiamo riproposto la stessa
domanda e una bambina ha detto “è
“ difficile”, mentre un bambino ha detto “èè poco probabile”.
probabile
EDiMaST — Volume 1, Number 1, May-August
May
2015
19
Babini Stefano, Graziani Ivan
Successivamente i bambini hanno effettuato estrazioni di una caramella in da un sacchetto
contenente caramelle nere e verdi in varie situazioni: prima 8 nere e 2 verdi, poi 7 nere e 3 verdi, fino
ad arrivare ad una stessa quantità dei due tipi. I bambini hanno così scoperto il concetto di probabilità
variabile (meno probabile e più probabile). Quando siamo arrivati ad avere 5 caramelle nere e 5 verdi,
una bambina ha detto “stessa probabilità”.
“E se ne estraiamo due per volta?” E' iniziata così la simulazione, con estrazione contemporanea di
2 caramelle per bambino, nella situazione di parità di caramelle (5 nere e 5 verdi). I bambini
rimangono stupiti quando vedono che nei loro sorteggi non vengono regolarmente estratte una
caramella nera e una verde come indicherebbe la probabilità teorica e questo è già un buon traguardo
per questo livello di scuola.
Anche nella prima classe della primaria abbiamo chiesto cosa intendessero per impossibile. Anche
in questo caso il concetto di impossibile si confondeva con quello di poco probabile, abbiamo quindi
riproposto la stessa attività sperimentata per l’infanzia col sacchetto di caramelle.
Siamo poi passati ad esaminare la probabilità legata al lancio di una moneta: “Se lanciamo una
moneta quanti sono i casi possibili?”. Risposta “testa e croce”. “Qual è la probabilità di ottenere
testa? E di ottenere croce?”. Un bambino risponde “metà e metà”.
Abbiamo notato che in classe c’era un dado di peluche, abbiamo quindi chiesto “Se ora lanciamo
questo dado a sei facce che probabilità abbiamo di ottenere 2?”. Una bambina ha detto “una su sei”.
Allora abbiamo chiesto, dal momento che avevamo già parlato di frazioni: “Quindi come indichereste
questa probabilità usando una frazione?”. La bambina ha risposto “uno su 6 è 1 ”.
6
“E con la moneta: la probabilità che esca testa?”. Subito ha risposto “ 1 ”.
2
Allora abbiamo chiesto ai bambini se conoscevano la differenza tra un numero pari e uno dispari.
Visto che la metà dei bambini erano in grado di distinguere tra i numeri compresi tra 1 e 6 quali erano
pari e quali erano dispari, abbiamo chiesto: “Qual è la probabilità di ottenere un numero pari
lanciando il dado?”. La risposta è stata 3 ma un bambino ha fatto notare che era la metà dei casi e
6
quindi anche 1 ; la discussione procede spontaneamente portando ad affrontare tanti concetti
2
importanti per le frazioni.
Nella seconda primaria abbiamo proposto lo stesso percorso seguito per la prima, ma abbiamo
aggiunto alcune domande relative al lancio di monete e di due dadi. “Se lanciamo due monete insieme
qual è la probabilità maggiore di accoppiata: Testa-Testa, Croce-Croce o Testa -Croce?”. I bambini
hanno risposto subito “è uguale”. Allora abbiamo rappresentato alla lavagna le varie possibilità,
verificando che era più probabile ottenere testa e croce perché si presenta in “2 casi su quattro”.
Domanda: “Se lanciamo due dadi insieme qual è la somma più probabile?”. Qui i bambini hanno
risposto un po’ a caso e diversi di loro si sono orientati verso la somma più alta 12. Abbiamo allora
simulato alla lavagna tutte le possibilità e i bambini si sono subito accorti che il 2 e il 12 si
comportavano nello stesso modo e potevano uscire solo in un caso: il 2 con 1 + 1 e il 12 con 6 + 6.
Quindi i due fanciulli che avevano proposto il 12 come somma più probabile non hanno avuto
conferma. Esaminando gli altri casi si nota che esistono due possibilità di ottenere 3 e 11 (1+2 e
2+1…), tre possibilità di ottenere 4 e 10 (1+3, 3+1 e 2+2….), quattro possibilità per 5 e 9 (6+3, 3+6,
4+5, 5+4…), cinque possibilità per 6 e 8 (1+5, 5+1, 4+2, 2+4, 3+3…). Si scopre infine che il
“vincitore” è il 7 con sei possibilità: 6+1, 1+6, 5+2, 2+5, 4+3, 3+4. “Viene fuori un triangolo” ha
notato una bambina.
Per finire abbiamo chiesto: “Se moltiplichiamo le due cifre: è più probabile che il prodotto sia pari o
dispari? Oppure la probabilità di ottenere un numero pari o dispari è la stessa?” Anche in questo
caso i bambini hanno risposto tutti “uguale”, ma poi suggerendo di pensare meglio una bambina ha
detto “E' maggiore la probabilità di ottenere un numero pari, perché con un numero pari ed uno
20
EDiMaST — Volume 1, Number 1, May-August 2015
Happy verticality in mathematics
dispari viene pari”. Abbiamo quindi simulato la situazione indicando con p il numero pari e con d il
dispari: p x p = p p x d = p d x d = d.
Una bambina ha detto: “Ma allora per avere dispari devono essere entrambi dispari quindi la
probabilità 1 su 3”.
Nella terza primaria abbiamo ripetuto la stessa attività, concentrandoci maggiormente sugli aspetti
legati alle frazioni.
Nella prima “media” abbiamo analizzato sperimentalmente i casi impossibili, certi e probabili
attraverso il lancio di un dado.
Domanda: “È possibile che lanciando un dado a 6 facce esca un 7?”
Risposta di tutta la classe “No”.
Domanda: “È possibile che lanciando lo stesso dado io ottenga un numero compreso tra 1 e 6?”.
Tutti: “Sì”.
Utilizzando situazioni reali è più facile formulare una risposta corretta.
Si può osservare anche che alcune situazioni sono meno probabili o più probabili di altre e ci siamo
collegati alle frazioni per rappresentare le situazioni.
Sempre con il dado:
Domanda: “Qual è secondo voi la probabilità di ottenere col lancio di un dado un numero
stabilito, ad esempio 5?”.
Risposta: “una su sei, perché sei sono i numeri possibili”.
Domanda: “Quindi in frazioni?”.
Risposta: “ 1 ”.
6
Domanda: “E qual è la probabilità di ottenere un numero pari oppure dispari?”
Risposta: “Sono entrambe 3 su 6, cioè 3 ”, un alunno ha notato: “che poi è 1 ”.
6
2
Abbiamo proposto un quesito di una prova INVALSI che ha ottenuto un numero rilevante di
insuccessi:: Tre amici devono stabilire chi di loro deve lavare i piatti. Decidono di fare testa o croce
lanciando due monete. Mario lava i piatti se escono due teste, Antonio se escono due croci e Paolo se
escono testa e croce. Avranno tutti la stessa probabilità di lavare i piatti? Motiva la tua risposta”.
Qualcuno ha risposto “Uguale”. Allora ho chiesto di ragionare e magari di provare a simulare la
situazione su un foglio. Un alunno è stato rapido e ha risposto “è più probabile che li lavi Paolo. È più
facile ottenere testa e croce perché si presenta in due casi su quattro, cioè 1 , mentre due teste o due
2
1
croci sono entrambe solo una su quattro cioè ”. Giusta la risposta e anche la motivazione.
4
Abbiamo rivolto le stesse domande sulle somme e i prodotti possibili lanciano due dadi come
avevamo già visto alla primaria.
Nella seconda classe delle “medie” dopo aver ripassato i concetti di certo, impossibile e probabile,
anche con esempi pratici come il lancio di dadi, abbiamo analizzato i casi di eventi compatibili e
incompatibili.
Abbiamo chiesto “Lanciando un dado, qual è la probabilità che escano un numero pari o un
multiplo di 3?”. I ragazzi hanno subito notato che tra i numeri pari c’è il 6 che è anche multiplo di 3 e
quindi i due casi erano compatibili. Per cui la probabilità diventava:
3
2
1
4
( pari ) + ( multipli ) − ( compatibile ) = .
6
6
6
6
EDiMaST — Volume 1, Number 1, May-August 2015
21
Babini Stefano, Graziani Ivan
Abbiamo proposto una prova analoga utilizzando carte da briscola (40 carte). La domanda qui è
stata: “Qual è la probabilità di estrarre a caso una carta di denari o un re?”. Anche in questo caso c’è
una compatibilità perché uno dei 4 re del mazzo è anche di denari.
Quindi si ottiene:
10
4
1
13 .
( denari ) + ( re) − ( compatibile) =
40
40
40
40
Nella classe terza della secondaria di primo grado abbiamo richiamato i casi visti nelle classi
precedenti e abbiamo aggiunto alcuni esempi di probabilità composta.
Abbiamo chiesto: “qual è la probabilità, lanciando due dadi, di ottenere due 5?”. Dopo alcuni
calcoli e ragionamenti uno studente ha risposto “ 1 ”. Abbiamo controllato il suo procedimento e
36
abbiamo notato che la sua risoluzione era grafica; aveva associato ad ogni numero del dado gli altri sei
possibili del secondo dado e quindi, visivamente, aveva trovato la risposta corretta. Allora ho invitato i
ragazzi a riflettere su come si poteva ottenere questo risultato partendo dalle due probabilità semplici.
Una ragazza ha risposto “Dal loro prodotto”.
Abbiamo voluto verificare se si otteneva lo stesso risultato calcolando la probabilità di ottenere due
numeri pari. Utilizzando lo schema del primo studente è stato facile vedere che era 9 = 1 .
36
4
Nella quinta ginnasio del liceo classico e in una seconda di scienze umane abbiamo tenuto due
lezioni sulla probabilità.
Nella prima lezione siamo partiti considerando un sacchetto contenente una pallina bianca e due
palline rosse.
Abbiamo proposto:
“Calcoliamo la probabilità di estrarre: una pallina bianca, una rossa, una verde o una qualsiasi”.
a) una pallina bianca ……………. P(B)= 1
3
b) una pallina rossa ………………. P(R)= 2
3
c) una pallina verde ……………… P(V) = 0 = 0
3
d) una pallina qualsiasi ………….. P= 3 = 1
3
Fig. 11 – Probabilità dei vari casi affrontati.
Siamo arrivati così a definire:
- la probabilità come il rapporto fra i casi favorevoli e i casi possibili
- evento impossibile (caso c)
- evento certo (caso d)
Abbiamo poi introdotto la probabilità dell’intersezione e dell’unione di due eventi: utilizzando un
diagramma ad albero (fig.12) dove B rappresenta la pallina bianca e R la pallina rossa, ottenendo:
22
EDiMaST — Volume 1, Number 1, May-August 2015
Happy verticality in mathematics
B
B
R
R
B
R
R
R
B
R
R
R
Fig. 12 – l’albero delle probabilità.
La probabilità di ottenere una pallina bianca alla prima estrazione e una bianca alla seconda (con
reinserimento) risulta, osservando l’albero 1 cioè esattamente 1 ⋅ 1 deduciamo quindi essa che
9
3 3
coincide con il prodotto tra P(B) e P(B).
Si giunge poi alla definizione della probabilità dell’intersezione e dell’unione di eventi seguendo
un procedimento simile per pervenire alla somma logica.
Nella seconda lezione abbiamo presentato la legge dei grandi numeri calcolando prima la
probabilità teorica nel lancio di una moneta (testa o croce).
Abbiamo poi suddiviso la classe in gruppi di due studenti, assegnando ad uno il compito di lanciare
la moneta e all’altro di registrare i dati su un foglio elettronico. Dopo 20 minuti di lanci abbiamo
raccolto i dati per osservare la probabilità empirica.
I ragazzi hanno così potuto osservare che con l’aumentare dei lanci la probabilità empirica tende a
coincidere con quella teorica.
Abbiamo quindi concluso presentando la legge dei grandi numeri.
Conclusione
Affrontare in verticale questi argomenti, opportunamente scelti, ci ha consentito innanzitutto di
confrontarci e consigliarci costantemente sulle metodologie adottate e di analizzare di volta in volta
quanto emerso nelle classi con i nostri studenti e con i docenti che abbiamo affiancato in questa
esperienza.
Un dialogo tra ordini di scuola diversi, oltre ad aumentare la conoscenza dei rispettivi curricoli,
arricchisce sicuramente la didattica degli insegnanti che sono disposti a mettersi in gioco.
Il fatto di affrontare alcuni argomenti particolarmente ostici in modo divertente e non del tutto
usuale ha consentito ai bambini e ai ragazzi di iniziare a capire che la matematica può essere anche
divertente. Ci ha permesso, inoltre, di iniziare a rimuovere alcuni luoghi comuni secondo i quali la
matematica viene identificata quasi esclusivamente con l’esecuzione di calcoli.
Lavorare in modo laboratoriale riporta la matematica alla sua connotazione originale e cioè alla
risoluzione di problemi di vario tipo.
Il progetto “Happy verticality in matematica” è servito a questo e a tanto altro. È un’attività che
consigliamo a tutti gli insegnanti, dall’Infanzia alla secondaria di II grado, senza controindicazioni.
EDiMaST — Volume 1, Number 1, May-August 2015
23
Babini Stefano, Graziani Ivan
Deposito dei materiali dell’attività
Al seguente link sono depositati eventuali materiali inerenti a questo articolo.. Nel tempo potranno
essere modificati e arricchiti seguendo l’evoluzione delle idee sottostanti o/ee future sperimentazioni
svolte dall’autore dell’articolo.
http://www.edimast.it/J/20150101/0005002
http://www.edimast.it/J/20150101/00050024BA/
Bibliografia
Montone Antonella, Fagiano Eleonora, Giuliano Fiorentino Michele,
Michele (2014). “I numeri razionali e le frazioni
giocando a carte” al Convegno UMI-CIIM
UMI
di Livorno 2014 www.umi-ciim.it/.../Montone_I
ciim.it/.../Montone_I-numerirazionali-e-le-frazioni-giocando.. (verificato in data 23/07/2015).
Fandiňo Pinilla Martha Isabel,, (2005). Le frazioni, Pitagora editrice, Bologna.
Balsimelli Sergio, (2009). La geometria con GeoGebra,
GeoGebra Matematicamente ed., Lecce.
Stefano Babini
Liceo “Rambaldi – Valeriani – A. Da Imola” di Imola (BO)
Via Guicciardini, 4 , 40026 Imola (BO)
[email protected]
[email protected]
Italy
Professore a tempo indeterminato di matematica
m
e fisica. Appassionato di problem
solving, di comunicazione
municazione didattica e delle nuove tecnologie applicate alla didattica
(docente da diversi anni in classi 2.0).
Si occupa inoltre di processi di apprendimento e di valutazione in vari contesti formativi
e di sistema.
Collabora da anni con l’INVALSI (Istituto Nazionale per la VALutazione del Sistema
educativo di Istruzione e di formazione).
formazi
Ivan Graziani
Istituto Comprensivo di Santa Sofia – Scuola Secondaria di I grado “Galileo
“
Galilei”
Via Arcangeli,
Arcangeli 1, 47018 Santa Sofia (FC)
[email protected]
Italy
Professore a tempo indeterminato di matematica. Formatore in didattica della
matematica. Appassionato di ICT, di problem solving e di comunicazione didattica. Si
occupa inoltre di processi di apprendimento e di valutazione in vari contesti formativi e
di sistema.
Collabora da diversi anni con l’Università di Bologna,, con l’INDIRE (Istituto Nazionale
di Documentazione, Innovazione e Ricerca Educativa), con l’INVALSI (Istituto
Nazionale per la VALutazione del Sistema educativo di Istruzione e di formazione) e con
l’USR Emilia Romagna (Ufficio Scolastico Regionale).
Received June 19, 2015; revised July 18, 2015; accepted August 10, 20155
Open Access This paper is distributed under the terms of the Creative
Commons Attribution 4.0 International (CC BY 4.0)
24
EDiMaST — Volume 1, Number 1, May-August 2015