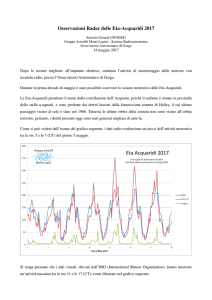
FUNZIONI LOGARITMO
A partire dalla conoscenza del grafico di f(x) = logx
disegna il grafico delle seguenti funzioni
g(x) = log(x+1) ;
g(x) = log(2x-1);
g(x) =2 + logx ;
g(x) =2 - logx ;
g(x) = |logx| ;
g(x) = log|x|
g(x) =| 2 - logx| ;
g(x) =1/ (2 + logx) ;
g(x) =1/ (2 - logx)
log(x+1) definito per x+1>0, quindi per x>-1; log(2x-1)
definito per 2x-1>0, quindi per x>1/2
Dal grafico di logx al grafico di 2+logx, traslando in verticale
di 2 unità verso l’alto; Dal grafico di logx al grafico di -logx
(simmetria rispetto all’asse x) al grafico di 2-logx, traslando
verso l’alto di 2 unità
Dal grafico di logx si ottiene il grafico di |logx|, con una
simmetria rispetto all’asse x per 0<x<1, inalterato per x>1
La funzione log|x| è pari e definita in R/{0}, quindi, per
ottenere il suo grafico, basta aggiungere il ramo per x<0
ottenuto dal grafico di logx con una simmetria rispetto
all’asse y
Grafico della funzione 1/(2+logx), si ha una singolarità in
x=e-2 . La funzione è definita per x>0 con x≠ e-2 . La funzione
è positiva per x> e-2 dove 2+logx>0. Determina i limiti ai
bordi del dominio……
FUNZIONI
Dare un esempio di funzione f(x) definita su R , che
sia decrescente, il cui limite per x→−∞ sia 0, e per
x→+∞ il limite sia −∞
Soluzione: Ce ne sono molte che soddisfano i requisiti
richiesti, ad esempio f(x)= -ex
Dare un esempio di funzione f(x) definita su R , che
sia decrescente, il cui limite per x→−∞ sia +∞, e
per x→+∞ il limite sia 0
Soluzione: Anche in questo caso ce ne sono molte che
soddisfano i requisiti richiesti, ad esempio f(x)= e-x
DISEQUAZIONI CON ESPONENZIALI
Determinare x tale che e3x-1= 2
Determinare per quali x si ha e3x-1≥ 2
SOLUZIONE:si applica il log in base e ad entrambi i
membri dell’uguaglianza, ottenendo 3x-1 =log2,
quindi x=(log2 +1)/3
La disequazione è soddisfatta per 3x-1≥log2, essendo la
funzione logaritmo in base e crescente, quindi si ha
x≥(log2 +1)/3
DISEQUAZIONI CON ESPONENZIALI
Determinare x tale che e1-2x= 3
Determinare per quali x si ha e1-2x < 3
SOLUZIONE:L’equazione è soddisfatta per 1-2x=log3,
quindi x= (1-log3)/2
La disequazione è soddisfatta per 1-2x<log3, quindi per
x> (1-log3)/2
DISEQUAZIONI CON LOGARITMI
Assegnata la funzione f(x)= 1/(1-2logx), determinare il
suo insieme di definizione; determinare per quali valori
x si ha f(x)>0.
SOLUZIONE: La funzione log ha per dominio x>0,
dobbiamo, inoltre, escludere la singolarità che si ha
per 1-2logx=0 quindi per x=e1/2
Insieme di definizione {x∈R| x>0 e x≠ e1/2 }
La funzione è positiva per 1-2logx>0, quindi per logx<1/2
Quindi essendo l’esponenziale in base e crescente, per
x< e1/2
Matematica e crescita di popolazioni….
- In una data popolazione, inizialmente costituita da 200
individui, il numero di individui varia dall’anno n
all’anno successivo n+1, secondo la seguente legge
an+1 = an + 0,4(1000 - an)
a) determinare il termine generale della
successione
b) al passare del tempo, a quale valore limite tende
an?
Matematica e crescita di popolazioni….
Cerchiamo di trasformare la successione assegnata
an+1 = an + 0,4(1000 - an)
a0 = 200
in una successione geometrica (analoga a quella della
duplicazione dei batteri…).
Si sottrae, ad ambo i membri della relazione che definisce
la successione per ricorrenza, il numero 1000
an+1 -1000= an -1000 + 0,4(1000 - an)
Matematica e crescita di popolazioni….
Chiamando con xn = an -1000, otteniamo
xn+1 = xn -0,4 xn = 0,6 xn
x0 = -800
Quindi il termine generale è xn = -800(0,6)n
Il termine generale della successione assegnata è perciò
an =1000 + xn =1000 - 800(0,6)n
La successione an , al crescere di n, tende al valore 1000
Matematica e crescita di popolazioni….
Una popolazione evolve secondo la legge
N(t)= 50/(1 + 4e-0.7t)
dove N(t) indica il numero di individui presenti nella
popolazione al tempo t.
Disegna il grafico di N(t) anche per t<0
SOLUZIONE: La funzione è definita su R ed è sempre
positiva. Per t→-∞ , N(t)→0, mentre per t→+∞
N(t)→50. Intersezione con asse delle ordinate
N(0) = 10. Il valore 25 (punto di mezzo nell’intervallo
immagine (0,50)) viene raggiunto per t =log4 /0.7
Grafico della funzione N(t)=50/(1 + 4e-0.7t)