FISICA 2----QUESITI SECONDA PARTE
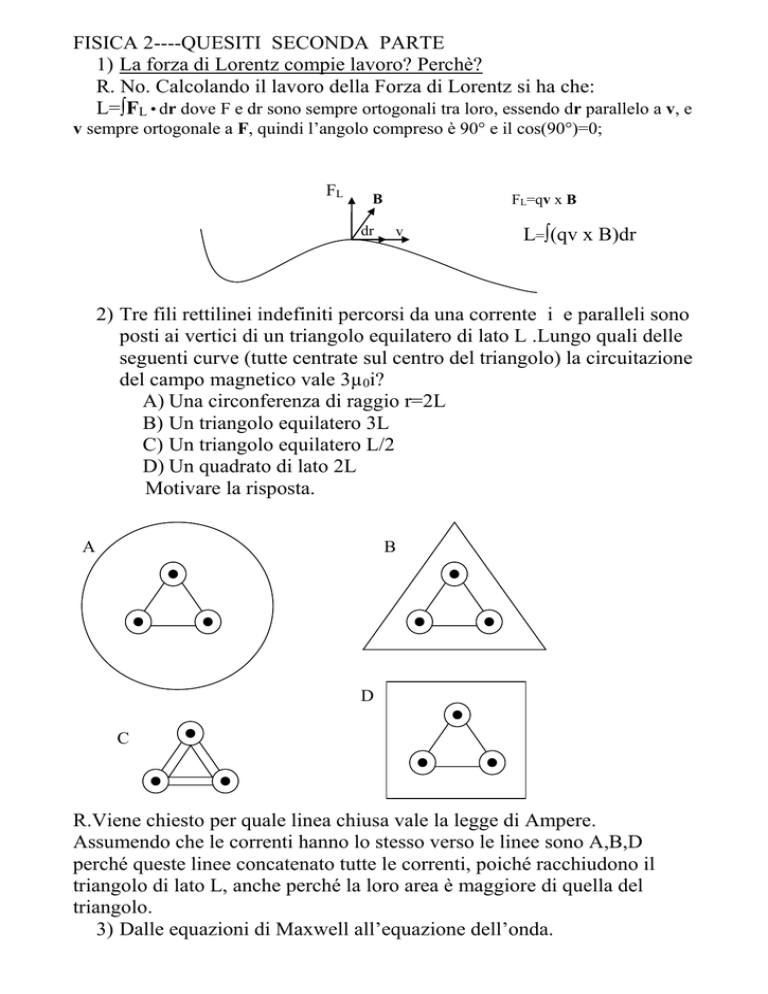
1) La forza di Lorentz compie lavoro? Perchè?
R. No. Calcolando il lavoro della Forza di Lorentz si ha che:
L=∫FL • dr dove F e dr sono sempre ortogonali tra loro, essendo dr parallelo a v, e
v sempre ortogonale a F, quindi l’angolo compreso è 90° e il cos(90°)=0;
FL
B
dr
FL=qv x B
v
L=∫(qv x B)dr
2) Tre fili rettilinei indefiniti percorsi da una corrente i e paralleli sono
posti ai vertici di un triangolo equilatero di lato L .Lungo quali delle
seguenti curve (tutte centrate sul centro del triangolo) la circuitazione
del campo magnetico vale 3µ0i?
A) Una circonferenza di raggio r=2L
B) Un triangolo equilatero 3L
C) Un triangolo equilatero L/2
D) Un quadrato di lato 2L
Motivare la risposta.
A
B
D
C
R.Viene chiesto per quale linea chiusa vale la legge di Ampere.
Assumendo che le correnti hanno lo stesso verso le linee sono A,B,D
perché queste linee concatenato tutte le correnti, poiché racchiudono il
triangolo di lato L, anche perché la loro area è maggiore di quella del
triangolo.
3) Dalle equazioni di Maxwell all’equazione dell’onda.
4) Discutere analogie e differenze tra campi elettrici prodotti da cariche
statiche e campi elettrici indotti.
R. Le cariche statiche non producono corrente e generano campi
elettrici conservativi, i campi elettrici invece sono generati da corrente
e non sono conservativi in quanto L =∫ Fe ds L=∫q0 E ds
q0∫
E ds
L/ q0 =∫E ds dove L/q0= ε quindi ε=∫E ds ma per la legge di
Faraday-Lenz ε = - dφ(B)/dt quindi ∫E ds= - dφ(B)/dt ed è diverso da 0.
5) La forza di Lorentz è una forza conservativa? Perché?
No. Perché non compie lavoro.
6) Discutere analogie e differenze tra la legge di Coulomb e la legge di
Biot-Savart.
Legge di Coulomb
F=1/(4πε0) Q1Q2/r2
Legge Biot-Savart
dB=μ0/4π i dl x r/r3
prodotto vettoriale()
Inversamente proporzionale alla
Direttamente proporzionale alla
costante dielettrica nel vuoto;
costante di permeabilità magnetica
Generato da cariche statiche, ferme; nel vuoto;
Generato da correnti(cariche in
movimento);
Entrambi vanno come 1/r2
7) E’ possibile generare un campo magnetico senza utilizzare magneti o
correnti? Perché?
Si. Dalla legge di Ampere-Maxwell abbiamo che ∫B dl= μ0 ε0 dφ(E)/dt
Maxwell mette in relazione il B con la variazione di flusso del E nel tempo.
Ampere dimostra che ∫B dl= μ0ich quindi si ha:
∫B dl= μ0ich+ μ0 ε0 dφ(E)/dt se abbiamo corrente nulla sopravvive la (μ0 ε0
dφ(E)/dt) e quindi si avrà B con la variazione di flusso del E nel tempo.
8) Discutere la legge della circuitazione di Ampere legata alla corrente
di spostamento.
R. La corrente di spostamento è una corrente fittizia che non genera
spostamento di carica ed è stata introdotta da Maxwell per giustificare
la legge di Ampere tra le piastre di un condensatore ed è definita come:
is= ε0 dφ(E)/dt quindi la legge di Ampere ∫B ds= μ0 (ich+ is) sostituendo si
ha: ∫B ds= μ0ich+ μ0ε0 dφ(E)/dt
9) Enunciare e discutere brevemente il significato fisico delle quattro
equazioni di Maxwell.
Legge Gauss campo elettrico ∫E dA=qch/ ε0 lega il flusso elettrico netto alla
carica elettrica netta racchiusa
Legge di Gauss per il campo magnetico ∫B dA=0 lega il flusso magnetico netto
alla carica magnetica netta racchiusa
Legge di induzione di Faraday ∫E ds= - dφ(B)/dt lega il campo elettrico indotto
alla variazione di flusso magnetico
Legge di Ampere-Maxwell ∫B ds= μ0ich+ μ0ε0 dφ(E)/dt lega il campo
magnetico indotto alla variazione di flusso elettrico e alla corrente
10)
Enunciare il teorema della circuitazione di Ampere, discuterne
l’importanza per la determinazione del campo di induzione
magnetica ed utilizzarlo per il calcolo di B generato da un soleinoide.
La circuitazione del campo magnetico è uguale a μ0 ich dove ich è la
somma algebrica delle correnti concatenate dalla linea chiusa
∫B dl = μ0ich
La legge di Ampere è molto utile per calcolare B specialmente quando
si possono assumere determinate simmetrie in modo da facilitare il
calcolo dell’integrale, per esempio quando B è costante sulla linea
chiusa.
Nel caso del solenoide
1
4
B
2
3
Prendiamo come linea chiusa una spira rettangolare, perché ha la stessa
direzione del campo, e calcoliamo quando vale B generato dal solenoide
con il teorema di Ampere:
vediamo che sui lati 2 e 4 ∫B dl=0 perché essendo un prodotto scalare
fra vettori si ha: ∫B dl cosθ ma θ=π/2 cosθ=0 poiché B e dl sono
ortogonali;
sul lato 3 B=0 quindi ∫B dl=0;
per il lato 1 ∫B dl cosθ =μ0ich ma θ=0 cosθ=1 quindi si ha:
∫B dl=μ0ich essendo B costante nel solenoide si ha: B∫ dl=μ0ich
dove ich= alla somma di tutte le correnti concatenate se N=numero di
spire ed I la corrente che attraversa il solenoide allora ich=NI e si ha:
B= μ0NI/Liversore
11)
L’andamento del campo di induzione magnetica in funzione
delle correnti che lo generano può essere dedotto mediante la legge
di Ampere e/o la legge di Biot-Savart. Scrivete e commentate la
forma matematica di queste leggi,e descrivete significato,proprietà e
conseguenze fisiche.
Legge di Ampere
Legge Biot-Savart
dB=μ0/4π i dl x r/r3
∫B dl = μ0ich
Integrale su linea chiusa;
prodotto vettoriale( da come
prodotto scalare, mi da uno
risultato un vettore conserva il verso
scalare(il modulo di B), il verso è
del verso)
determinato con la regola della
Direttamente proporzionale alla
mano dx.
costante di permeabilità magnetica
ecc.(vedi sopra)
nel vuoto;
Generato da correnti(cariche in
movimento);
12)
Descrivete il fenomeno della corrente di spostamento e come
tale fenomeno modifica la legge di Ampere.
Vedi 8












