Distorsione
Armonica
(3)
1) Effetti correlati alla distorsione armonica
Dalla definizione di THD:
pftrue
P
Vrms I rms
P
2
THDV
THDI
V1,rms I1,rms 1
1
100
100
2
In presenza di una ridotta distorsione di tensione, si ha:
pftrue
P1
V1,rms I1,rms
1
THDI
1
100
2
pf disp
1
THDI
1
100
In altre parole, in presenza di armoniche il pf true (capacità di
2
trasferire potenza attiva senza impegnare troppo il sistema a monte)
è sempre inferiore al pfdisp (ovvero quanto appare alla fondamentale)
pftrue
pf disp
2) Effetti correlati alla distorsione armonica
Aumento delle perdite di potenza attiva:
Nei conduttori: per effetto pelle, aumentano anche a pari Irms
R I
2
i rms,i
R eq I 2rms
i
A pari Irms,1, aumentano per la presenza dei termini armonici RiIi2
Nel ferro: aumentano particolarmente le perdite per isteresi (≡cicli/s)
Conseguente riduzione della massima potenza attiva sopportabile
dai componenti del sistema (“derating”)
3) Effetti correlati alla distorsione armonica
Nei sistemi elettrici BT, si ipotizza generalmente che i carichi
alimentati siano equilibrati o che comunque il loro grado di squilibrio
sia modesto; di conseguenza la corrente che attraversa il conduttore
neutro è in teoria nulla, in pratica molto modesta.
Ciò ha come conseguenza che il conduttore di neutro risulta spesso
sottodimensionato rispetto ai conduttori di fase.
L’eventuale presenza di armoniche può portare ad uno stato di
funzionamento del sistema completamente diverso.
Limitandoci per semplicità alla sola presenza della 3a armonica di
corrente (in ciascuna delle 3 correnti di fase) e ricordando che in caso
di uguaglianza delle 3 forme d’onda di corrente le 3 componenti
di 3a armonica sono di sequenza omopolare (quindi tra loro in fase),
il conduttore di neutro viene attraversato da una corrente di 3a
armonica pari a 3 volte la corrente di 3a armonica di ciascuna fase.
Esempio: supponiamo di avere una componente di 3a armonica pari
al 30% della fondamentale; la corrente nel conduttore di neutro sarà:
I N eff
I F eff
3 0.3
1 0.32
0.9
0.86
1.044
Con una componente di 3a armonica pari invece al 70% della
fondamentale, la corrente nel conduttore di neutro diventa:
I N eff
I F eff
3 0.7
2.1
1.72
2
1.22
1 0.7
Si capisce quindi come la corrente di 3a armonica possa creare
problemi di adeguatezza del neutro in termini di portata di corrente
(oltre che di perdite di potenza attiva e di c.d.t.).
4) Effetti correlati alla distorsione armonica
Fenomeno 1: Le armoniche di tensione, anche se di entità modesta,
possono portare a tensioni di picco anche decisamente superiori a
quelle corrispondenti alla tensione nominale di rete
La condizione peggiore è ovviamente quella in cui le armoniche
hanno tutte la stessa fase della fondamentale.
Questo fenomeno può portare al superamento della rigidità
dielettrica dell’isolante del condensatore.
Fenomeno 2: consideriamo adesso le armoniche di corrente
assorbite dal condensatore:
ik yk vk (k 0 C ) vk
Anche assumendo che vk scenda rapidamente all’aumentare
dell’ordine di armonica, il fattore moltiplicatore k fa sì che le correnti
armoniche assorbite dal condensatore si possano mantenere
sostenute anche per k elevati.
Questo fenomeno può portare ad un aumento anche consistente della
temperatura di connessioni, terminali e piastre (e, per vicinanza, del
dielettrico), con riduzione della capability ma soprattutto della
rigidità dielettrica si amplifica il fenomeno 1.
5) Effetti correlati alla distorsione armonica
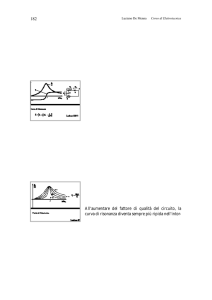
Possibili risonanze parallelo sui condensatori di rifasamento.
Xcc
Lcc
Crif
Circuito utilizzabile per lo studio delle frequenze di risonanza
del sistema, in presenza dei condensatori di rifasamento
(risonanza parallelo):
Xcc
Lcc
Crif
Se la frequenza di risonanza del circuito è molto vicina a quella
di una armonica assorbita dal carico, a tale frequenza il circuito
presenta una impedenza elevatissima e quindi vk può essere molto
elevata anche in corrispondenza di una ik contenuta
f ris
1
2 Lcc Crif
Ricordando che:
X cc ,1 2 f n Lcc
Yrif 2 f n Crif
e moltiplicando e dividendo per il quadrato della tensione nominale:
f ris
1
fn
2
X cc Yrif U n
2
2
fn
Un
1
X cc
2
U
n Yrif
2
Un
fn
Pcc
Qrif
Anche se le correnti armoniche originarie sono piccole, la tensione
all’armonica di risonanza può essere anche molto elevata
Il THDV cresce conseguentemente!
Questo fenomeno (condensatore di rifasamento come elemento di
amplificazione della distorsione armonica) non è disgiunto dai due
fenomeni precedenti, in cui i condensatori sono vittima delle
distorsioni
In altre parole, i condensatori di rifasamento mal accordati
con la Pcc della rete diventano al contempo concause e vittime della
distorsione armonica.
In generale, più è elevata la Pcc nella sezione di rete di interesse,
maggiore è la frequenza di risonanza. Poiché in generale
all’aumentare della frequenza si riduce il modulo dell’armonica di
corrente, ne consegue che quanto più elevata è la Pcc nella sezione
di rete di interesse tanto minore è l’effetto dell’eventuale risonanza.
5
7
Non sempre si conosce la Pcc nella sezione di rete di interesse. In
tale evenienza si può fare riferimento alla Pn-tras del trasformatore
immediatamente a monte. In tal caso si può scrivere:
Pcc 3 U n I cc 3 U n
Un
3 X cc
U n2
Pn tras
U n2
vcc p.u .
xcc
Pn tras
6) Effetti correlati alla distorsione armonica
Ulteriori effetti indesiderati correlati alla distorsione armonica
sono i seguenti:
Aumento delle problematiche di compatibilità e.m.
della rete, con maggior probabilità di malfunzionamenti di
alcune apparecchiature ad essa collegate (strumentazione di
misura, contabilizzazioni e protezioni, protezioni elettroniche,
interferenze con sistemi di TLC).
Presenza in rete di correnti di 5a armonica, che interferiscono
con i motori asincroni (si ricorda che tale armonica è di
sequenza inversa e come tale induce nei motori sia una coppia
costante contro-rotante che una vibrazione a 300Hz per
interazione con la fondamentale).