Problemi di termometria, dilatazione termica, calorimetria, leggi dei gas
Termometria
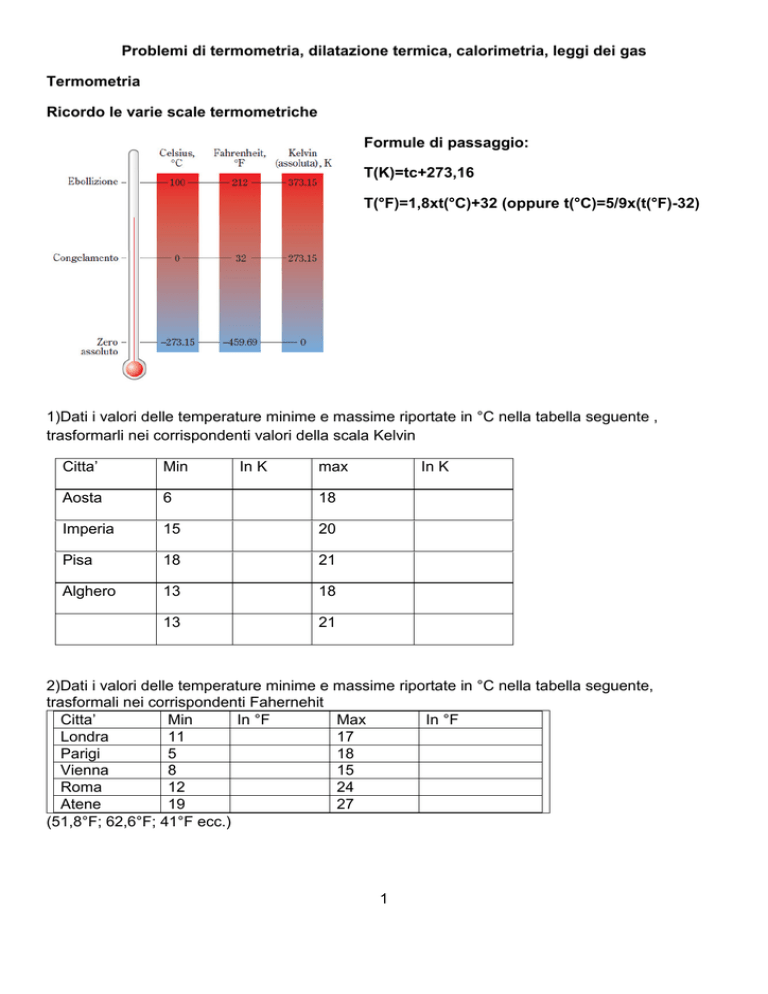
Ricordo le varie scale termometriche
Formule di passaggio:
T(K)=tc+273,16
T(°F)=1,8xt(°C)+32 (oppure t(°C)=5/9x(t(°F)-32)
1)Dati i valori delle temperature minime e massime riportate in °C nella tabella seguente ,
trasformarli nei corrispondenti valori della scala Kelvin
Citta’
Min
In K
max
Aosta
6
18
Imperia
15
20
Pisa
18
21
Alghero
13
18
13
21
In K
2)Dati i valori delle temperature minime e massime riportate in °C nella tabella seguente,
trasformali nei corrispondenti Fahernehit
Citta’
Min
In °F
Max
In °F
Londra
11
17
Parigi
5
18
Vienna
8
15
Roma
12
24
Atene
19
27
(51,8°F; 62,6°F; 41°F ecc.)
1
3)Quali delle seguenti formule sono corrette?
a)tF=32+1,8tC
b)Tk=tC-273,16
c)tC=Tk-273,16
d)tC=TK+273,16
e)tF=(32+1,8):tC
f)tC=(tF-32):1,8
4)Mettiti alla prova e calcola
Che cosa sfrutta il termometro per misurare la temperatura? (Più di una risposta è esatta.)
L’equilibrio termico.
La dilatazione termica.
I cambiamenti di stato.
La scala termometrica Kelvin.
5)Completa la tabella. La seguente tabella riporta alcune temperature notevoli in kelvin e gradi
Celsius. Completala inserendo i dati mancanti.
T(K)
t(°C)
Zero assoluto
0
Ghiaccio fondente
0
Temperatura ambiente
300
Temperatura corpo umano
37
Acqua bollente
100
6)La temperatura all’interno dell’aula è di 18 °C. In un giorno di primavera, la temperatura esterna
è più alta di 7,0 °C.Quanto vale la differenza di temperatura fra l’esterno e l’interno espressa in
kelvin?
7)Alla pressione di 1 atm, un blocco di argento e uno di oro iniziano a fondere rispettivamente alle
temperature di 1234 K e 1065 °C. Quale dei due elementi fonde a temperatura maggiore?
8)Nella scala di temperatura Fahrenheit, adoperata negli USA, l’acqua bolle a 212 °F e il ghiaccio
fonde a 32 °F. L’intervallo fra queste due temperature è diviso in 180 parti, e ognuna di queste
rappresenta un grado Fahrenheit (°F). A quanti gradi Celsius corrisponde la temperatura di 100 °F?
[R: 38 °C]
9)A quanti gradi Fahrenheit corrispondo 10 gradi centigradi?
10)La temperatura di ebollizione dell’acqua di mare è pari a 103 gradi centigradi. A quanti gradi
Fahrenheit corrisponde questo valore?
11)A quanti gradi centigradi corrispondo 100 gradi Fahrenheit?
12)Per friggere nell’olio delle patatine la temperatura ideale è di circa 150 °C. Dovendo indicarla in
gradi Fahrenheit che valore riporteresti?
13)Per friggere nell’olio cibi infarinati la temperatura ideale è 180/190 °C. Dovendo indicarla in
gradi Fahrenheit che valore riporteresti?
14)A quanti gradi Fahrenheit corrispondo 30 gradi centigradi?
2
15)In una giornata di primavera la temperatura esterna è di 20 °C. Dovendo indicarla a un amico
inglese in gradi Fahrenheit che valore diresti?
16)La carta brucia a 451 °F. A quanti gradi Celsius corrisponde questa temperatura?
17)Nella sala in cui si svolge un convegno di fisici il termometro segna 292 K.
a)A quanto corrisponde in °C?
b)A quanto corrisponde in °F
R: 19°C; 66,2°F
18)Calcolare per quale valore della temperatura un termometro centigrado e un termometro con
scala Fahrenheit forniscono lo stesso valore. R: -40°C=-40°F
19)I congelatori sono normalmente impostati a circa −18 °C. A quanti gradi Fahrenheit
corrisponde questo valore di riferimento. Quale osservazione puoi fare sul risultato ottenuto?
20)L’argento fonde a 961 °C. A quanti Kelvin corrisponde questo valore, detto punto di fusione?
21)Il ferro fonde a 1535 °C. A quanti Kelvin corrisponde questo valore, detto punto di fusione?
A quanti gradi Kelvin corrispondo 10 gradi centigradi?
22)A quanti gradi centigradi corrispondo 400 Kelvin?
23)Il punto di ebollizione dell’alluminio è posto a 2792 K. A quanti gradi centigradi corrisponde
questo valore?
24)A quanti gradi centigradi corrispondo 273 Kelvin?
25)La temperatura di ebollizione dell’olio di oliva è pari a 300 gradi centigradi. A quanti gradi
Kelvin corrisponde questo valore?
26)Il punto triplo dell’acqua, in cui coesistono la fase solida, liquida e gassosa, è posto a 273,16 K.
A quanti gradi centigradi si trova il punto triplo?
27)L’alluminio fonde a 868,15 K. A quanti gradi centigradi corrisponde questo valore, detto punto
di fusione?
28)L’acqua bolle a 100 °C alla pressione di 1 atm, a livello del mare. Ad alta quota l’acqua può
bollire a 90 °C, per la minor pressione. Un termometro Fahrenheit che temperatura indicherebbe?
29)Per friggere nell’olio cibi in pastella la temperatura ideale è di 338 °F. Dovendo indicarla in
gradi centigradi che valore riporteresti?
30)In una giornata invernale la temperatura esterna è a -2 °C (sotto zero). Dovendo indicarla a un
amico inglese in gradi Fahrenheit che valore diresti?
31)Descrivi i due sistemi di riferimento utilizzati da Celsius per costruire la scala termometrica che
porta il suo nome.
3
32)La scala della temperatura assoluta consente di esprimere la temperatura:
a) in gradi Celsius
b) con valori positivi e negativi
c) senza valori positivi
d) con valori anche molto bassi e senza valori negativi
33)Se la temperatura di una fredda giornata invernale è di –11 °C, quale valore leggeremmo se la
scala del termometro fosse tarata in kelvin?
34)Negli Stati Uniti la temperatura viene espressa in gradi Fahrenheit (°F).
a) Credi di poter fare il bagno se la temperatura dell’acqua è 30 °F?
b) Se la temperatura di un sistema aumenta di 10 °C, di quanti gradi Fahrenheit aumenta?
35)Uno studente ha misurato che passando dal giorno alla notte la temperatura dell’aria si è
abbassata di 7,8 °C. Quanto vale la diminuzione espressa in kelvin?
36)Utilizzando un termometro, uno studente ha misurato ogni due ore la temperatura e ha
compilato la seguente tabella:
Tempo (ora del giorno)
8
10
12
14
16
18
20
22
24
Temperatura (°C)
-1
1
3
5
6
6
4
1
-3
Sapendo che per escursione termica si intende la differenza tra la temperatura massima e quella
minima:
a) calcola il valore dell’escursione termica tra le ore 8 e le ore 10.
b) in quale intervallo di tempo di due ore si è registrata la massima escursione termica?
c) calcola il valore dell’escursione termica nell’intervallo di tempo dalle ore 8 alle ore 24.
37)La temperatura in una palestra è di 18 °C mentre all’esterno il termometro segna la
temperatura di 25°C. Quanto vale la differenza di temperatura fra l’esterno e l’interno espressa in
kelvin? Ed espressa in gradi celsius?
38)Nonostante che le scale termometriche Celsius e Fahrenheit siano diverse, esiste una
temperatura che è espressa dallo stesso valore in entrambe. Qual è questo valore?
39)Un filo elettrico di rame fonde alla temperatura di 1083 °C mentre in un fusibile il filo di stagno
fonde a 232 °C. Quale calcolo si deve fare per esprimere la differenza tra queste temperature
nella scala Fahrenheit?
4
40)In una stanza è collocato un termometro che riporta sia la scala Celsius sia la scala
Fahrenheit. Se la temperatura della stanza passa da 18 °C a 23 °C, puoi con sicurezza affermare
che:
a) la temperatura indicata nella scala Fahrenheit è di 23 °F
b) la temperatura è aumentata esattamente di 5 °F
c) la temperatura è aumentata di 9 °F
d) la temperatura è diminuita di 5 °F
e) la temperatura indicata nella scala Fahrenheit è di 55 °F
41)A proposito della scala termometrica Kelvin quale affermazione è sbagliata?
a) Si chiama anche scala assoluta delle temperature
b) Il suo valore più basso corrisponde a 2273 °C
c) Presenta più valori positivi che valori negativi
d) Il suo valore più basso è zero
e) L’espressione 20 K si legge venti kelvin
42)Uno studente versa acqua del rubinetto in due contenitori e li riscalda separatamente; in un
caso la temperatura aumenta di 20 °C e nell’altro di 20 °F. Dove si trova l’acqua più calda?
43)Alla pressione di 1 atm, un blocco di argento e uno di oro iniziano a fondere rispettivamente
alle temperature di 1234 K e 1065 °C. Quale dei due elementi fonde a temperatura maggiore?
44) Nella scala di temperatura Fahrenheit, adoperata negli USA, l’acqua bolle a 212 °F e il
ghiaccio fonde a 32 °F. L’intervallo fra queste due temperature è diviso in 180 parti, e ognuna di
queste rappresenta un grado Fahrenheit (°F) A quanti gradi Kelvin corrisponde la temperatura di
100 °F? R: 38°C=311K
Dilatazione lineare
1)Un cursore per tende è formato da un profilato di alluminio lungo 2,4 m a 12 °C. Quanto sarà
lungo quando, esposto al sole, raggiungerà la temperatura di 50 °C?
(λalluminio=23,8·10-6 °C-1)(R: 2,402 m)
2) Un filo di rame è lungo 150 m a 20 °C. Calcola la sua lunghezza a 100 °C. (λarame = 1,7·10-5
°C-1).(R: 150,204 m
3) Un filo metallico è lungo 100,00 m alla temperatura di 24 °C, mentre a 100 °C misura 100,08 m.
Indica il coefficiente di dilatazione lineare del materiale di cui è fatto il filo. (R: 10,52 10-6 °C-1
4)Due sbarre, una di ferro e una di ottone hanno, a 0°C, la stessa lunghezza, di 160 cm. A quale
temperatura le loro lunghezze differiranno di 2 mm? (λferro = 1,2·10-5 °C-1 λottone = 1,9·10-5 °C-1)
(R: 178 °C.)
5)Una sbarra di piombo (λPb=29 10-6 °C-1)alla temperatura di 0°C e’ lunga 120m. Calcolare la
lunghezza finale della sbarra sapendo che la temperatura e’ stata portata a 120°C (R:120.4176m)
6)Determinare la natura di una sbarra metallica sapendo che la sua lunghezza iniziale e’ pari a
12m e che la sua temperatura e’ stata portata da 10°C a 180°C, subendo un allungamento pari a
0,05 m.(R: λ=:24 10-6 °C-1 alluminio)
5
7)Determinare la lunghezza iniziale di una sbarra di ferro (λFe=12 10-6 °C-1) sapendo che essa
subisce un allungamento pari a 0,2m quando la sua temperatura viene portata da 120°C a 210°C
(R:185m)
8)Una sbarra di oro (λAu=14 10-6 °C-1) di lunghezza iniziale pari a 2m subisce un allungamento di
0,002m. Determinare la variazione di temperatura alla quale e stata sottoposta la sbarra..(R:71°C)
9)Di quanto varia la lunghezza di una sbarra di ferro che ha, a 0 ° C, una lunghezza di 20 m se
fosse portata alla temperatura di 50 ° C ?(coefficiente di dilatazione lineare del ferro λ= 1,2 • 10 -5
°C -1).(R:12mm)
10)Una sbarretta subisce una variazione di lunghezza di 2,4 mm in seguito ad una variazione di
temperatura di 100 °C. Se la lunghezza della sbarretta, a 0 ° C, è di 1 m, determinare il
coefficiente di dilatazione lineare della sostanza in esame.(R: λ=2,4• 10-5 ° C-1)
11)Un viadotto di cemento è lungo 1,500 km in inverno ad una temperatura di -10,0 °C. In estate
la temperatura raggiunge il valore di 40,0 ° C. Calcola la lunghezza del viadotto in estate
(coefficiente di dilatazione per il cemento λ = 1,5 • 10 -5 °C -1).
12)Una sbarra di alluminio, alla temperatura di 0° C, è lunga 50,000 mm. Calcola la nuova
lunghezza della sbarra se la temperatura sale a 40 ° C (coefficiente di dilatazione lineare
dell'alluminio λ=2,4 • 10 -5 k -1). E' possibile misurare tale variazione di lunghezza con una riga
millimetrata? (NO perche’….Spiega.)(R: 50,048 mm)
13)La lunghezza delle rotaie della linea ferroviaria Bari-Lecce è circa 155 km. Sapendo che il
coefficiente di dilatazione lineare dell’acciaio è λ= 1,05• 10-6 k-1 e supponendo che le rotaie siano
saldate con continuità, calcola di quanto varia la lunghezza complessiva se la massima variazione
stagionale di temperatura è di 40,0 °C.(R:6,51m)
-6
-1
14)Sono date due sbarre lunghe 1 m. La sbarra A è fatta di argento (λ = 19·10 °C ) e la sbarra B
-6
-1
di piombo (λ = 28·10 °C ). Se la temperatura passa da 0 °C a 50 °C, quale delle due sbarre
subirà l’allungamento maggiore?
(R:piombo)
15)Calcolare il coefficiente di dilatazione di un metallo non noto, sapendo che a °0 la sua
lunghezza è di 1,250 m e che a 296 °C la lunghezza è diventata di 1,254 m. (R: λ=10,81 10-6 °C-1)
-6
-1
16)Determinare la temperatura a cui è arrivata una sbarra di ferro (λ = 12·10 °C ), sapendo che
a 0 °C la sua lunghezza è di 4,50 m e che per tale aumento di temperatura ha raggiunto una
lunghezza di 4,55 m.(R:926 °C)
-5
-1
-5
-1
17)Due sbarre, una di ferro (λ1 = 1,2·10 °C ) ed una di rame λ2 = 1,7·10 °C ) sono saldate
insieme ad una estremità. La lunghezza totale alla temperatura t1 = 10 °C vale L1 = 80,0111 cm,
mentre alla temperatura t2 = 100 °C vale L2 = 80,111 cm. Calcolare la lunghezza delle due sbarre
alla temperatura t = 0 °C (R: L01 = 50 cm L02 = 30 cm)
6
18)Un trapezio isoscele ha i lati obliqui e la base maggiore costituite da tre sbarre di ferro (λ1 =
-5
-1
1,2·10 °C ) che alla temperatura t0 = 0 °C hanno tutte la stessa lunghezza L10 = 100 cm. La base
-5
-1
minore è costituita da una sbarra di rame (λ 2 = 1,7·10 °C ) che alla temperatura t0 ha una
lunghezza L20 = 99,85 cm. A quale temperatura il trapezio diviene un quadrato? (R:300°C)
19)Qual’ è la differenza tra i periodi di un pendolo semplice calcolati alle temperature t1 = 30 °C e
t2 = 60 °C se il pendolo batte il secondo T0 = 1 s alla temperatura t0 = 0 °C ed il coefficiente di
-5
-1
dilatazione lineare della sostanza di cui è fatto il filo è λ = 2,4·10 °C ?(R:3,7 10-4 sec)
20)Lo specchio di un telescopio astronomico posizionato in cima ad un alto monte, ha un diametro
di 5 m. Poiché tale ambiente è caratterizzato da un'escursione termica che può andare da -10°C a
+ 50°C calcolare la massima variazione del diametro dello specchio.( λvetro = 3,2 10-6 °C-1 )
(R: 0,96 mm)
21)Una bacchetta di rame ha un diametro di 10 cm e alla temperatura di 20°C si incastra
perfettamente, attraverso un foro, in una lamina di ottone. Se la temperatura sia della bacchetta
che della lamina viene portata a 1540 °C, la bacchetta sarà ancora perfettamente aderente al
foro? E se no valutare l'ampiezza dell'eventuale fessura che si crea tra la bacchetta ed il bordo del
foro. Si sappia che: λrame = 1,7 · 10-5 °C-1; λottone = 1,9 10-5 °C-1(R:la differenza tra i raggi delle
due circonferenze vale 0,015 cm)
22)Un righello di acciaio è caratterizzato da una scala di fondo graduata di 1 millimetro. Qual è la
massima escursione termica a cui può essere soggetto se si vuole mantenere una precisione
entro 0,001 mm delle tacche? λacciaio = 11 10-6 °C-1(R: 91 °C).
23)Un orologio con meccanismo a pendolo ha un periodo di 0,5 s quando la temperatura
ambiente è di 20°C. Durante l'estate la temperatura media diventa di 30°C, calcolare il periodo di
oscillazione del pendolo.
in cui L è la lunghezza del pendolo e g l'accelerazione di gravità. Coefficiente di dilatazione lineare
del metallo di cui è composto il pendolo λ = 10-6 °C-1
-6
-1
24)Un’asta di ferro (λ = 12·10 °C ) è lunga 30 m alla temperatura di 0 °C. Completa la seguente
tabella:
Δt (°C)
ΔL (m)
50
…
100
…
150
…
200
…
250
…
2) Elabora un grafico riportando sull’asse delle X le variazioni di temperature Δt e sull’asse
delle Y le variazioni di lunghezza ΔL
3) Che tipo di proporzionalità intercorre tra le variazioni di temperatura e le variazioni di
lunghezza?
7
Dilatazione volumica
25)In una sala, dove è allestita una mostra permanente di arte contemporanea, è posizionata una
scultura in vetro pirex a forma di cubo di lato 150 cm (coefficiente di dilatazione lineare del vetro
pirex λ= 3,0• 10-6 k-1 ). Se nel periodo estivo la temperatura nella sala aumenta di 8,0 °C, di
quanto varia il volume della scultura?(R: 2,4• 102 cm3)
26)Una sostanza allo stato liquido occupa a 0° C un volume pari a 30 cm3. Sapendo che alla
temperatura di 50°C il suo volume aumenta di 0,27 cm3, determina in base al coefficiente di
dilatazione volumica se la sostanza in questione è mercurio (α=1,8 • 10-4 k-1), oppure petrolio
(α=1,8 • 10-4 k-1). R(mercurio)
27)Una colonna di mercurio ha un volume di 10,00 cm3 alla temperatura di 273 k. Il coefficiente di
dilatazione volumica del mercurio è α= 182 10 -6 k -1. Di quanto aumenta il volume del mercurio se
la sua temperatura sale a 373 K?(R:0,182cm3)
28)Un volume iniziale di mercurio (αCu=1,8 10-4 °C-1)pari a 4,3dm3 subisce una variazione di
volume uguale a 0,25dm3. Determinare la variazione di temperatura alla quale e’ stato sottoposto
il mercurio(R:322°C)
29)Determinare la natura del liquido contenuto all’interno di un recipiente sapendo che il suo
volume iniziale e’ pari a 3dm3 e che esso varia di 0,0432dm3 quando viene portato da una
temperatura di 50°C a una di 70°C, (R: α=7,2 10-4 °C-1 olio)
30)Determinare il volume iniziale di alcool etilico (αalcool=1,1 10-3 °C-1)contenuto all’interno di un
recipiente, sapendo che il suo volume aumenta di 2 dm3 quando la temperatura passa da 0°C a
100°C (R:1,81dm3)
31)Un’automobile ha un serbatoio di 75l e viene riempito di benzina (αbenzina=9,5 10-4 °C-1) quando
la temperatura dell’ambiente e’ di 12°C. L’automobile viene parcheggiata sotto il sole, quando la
temperatura atmosferica raggiunge i 38°C. Supponendo trascurabile la dilatazione del serbatoio,
quanta benzina trabocca?(R:1,8525l)
32)Una sfera di vetro, alla temperatura ambiente di 20 °C, ha diametro 30 cm. Calcola di quanto
aumenta il suo volume se la si riscalda a 70 °C. λ vetro = 2,5·10-5 °C-1)(R: 17 cm3)
33)Alla temperatura di 0°C viene misurato lo spigolo di un cubo di ferro che risulta lungo 50 cm.
Quale sarà il volume del cubo in seguito al riscaldamento dello stesso fino ad una temperatura di
350°C? Quale la variazione volumica in percentuale? (R: 126575 cm3; 1,26%)
-6
-1
34)Sono dati due cubi di lato 1,3 m. Il cubo A è fatto di alluminio (λ = 23,36·10 °C ) ed il cubo B
-6
-1
di ghisa (λ = 10,75·10 °C ). Se la temperatura passa da 0 °C a 100 °C, quale dei due cubi subirà
la dilatazione maggiore?(R:alluminio)
35)Un contenitore cilindrico di vetro con diametro di 8,0 cm e altezza 25,0 cm, chiuso
ermeticamente e senza aria all’interno, è riempito di mercurio fino a un’altezza di 24,7 cm alla
temperatura di 0 °C. Ipotizzando che quest’ ultima salga a un valore di 45 °C, stabilisci se il
contenitore di vetro, di cui si può trascurare la dilatazione, rischia di rompersi oppure no. (R: Il
contenitore di vetro non si rompe in quanto il suo volume è superiore al volume dilatato del
mercurio:
8
Esercizi di calorimetria
Applicazione della legge Q=cs·m·∆t (dove C=csm e’ detta capacita’ termica)
La capacita’ termica e’ la quantita’ di calore necessaria per far aumentare di un grado la
massa m di un corpo.
E’ utile parlare di capacita’ termica al posto di calore specifico quando ad esempio si parla
della capacita’ termica della Terra. Essendo composta da minerali di differente natura
chimica non ha senso parlare di calore specifico ma e’ piu’ utile il concetto di capacita’
termica perche’ non e’ riferito alla massa di un Kg.
1)Specificare quanta energia si deve comunicare ad una massa m = 32Kg di ferro puro
(cFe = 0; 5KJ/Kg°C) per portarla da T0 = 25°C alla temperatura di fusione Tf = 1750°C
(2; 76·107 J)
2) Quanto vetro si riesce a raffreddare da T0 = 10°C a Tf = -5°C sottraendo Q = -103 J di calore? Il
calore specifico del vetro vale cs = 0; 2Kcal/Kg /°C (0; 0079Kg)
3) Comunicando Q = 500KCal ad un corpo di massa m = 2Kg, si innalza la sua temperatura di
45°C. Quanto vale la capacità termica di quel corpo? (La capacità termica e’ il prodotto tra il calore
specifico e la massa del corpo. Cioè C= cs m.)( 46:511; 11J/°C)
4)Un blocco di rame di massa mCu = 5g si trova a una temperatura iniziale Ti = 25◦C. Al blocco
viene fornito un calore Q = 120J. Determinare la temperatura finale Tf del blocco sapendo che il
calore specifico dl rame è cCu = 0.093cal/g◦C .(86.7◦C)
5)Un corpo di massa m = 1 kg dopo aver assorbito una quantità di calore pari a 30 cal varia la sua
temperatura di 10 °C. Calcolare il calore specifico e la capacità termica del corpo. (C=m·cs=3·10-3
cal/g °C·1000g=3 cal/°C)
6)Una certa sostanza ha una massa molare di 50 g/mol. Quando vengono forniti 314 J di calore a
30:0 g di un campione di questa sostanza, la sua temperatura sale da 25:0 a 45:0 °C. Trovare il
calore specifico della sostanza , il numero di moli di cui è composta. E il calore specifico molare (
La massa molare è la massa in grammi di una mole della sostanza, ricorda anche che m=nM), il calore specifico
molare e’ il calore specifico di una mole quindi….)
(cs(molare)=26,2 J/mole °C)
7)Una pentola d'acqua contiene m = 10 l di liquido inizialmente alla temperatura di T0 = 18C. Il
liquido viene riscaldato fino a 50C e quindi si immerge nella pentola un vaso di vetro (cs =
1800J/Kg° C), innalzando la temperatura del materiale di 76C. Quale è la massa del vaso?( 9;
79Kg)
9
Temperatura di equilibrio
8) Due masse d'acqua, m1 = 23 l e m2 = 52 l sono a differenti temperature: T1 = 32°C e
T2 = 54°C. Se mescolate insieme, quale temperatura di equilibrio raggiungono?( 47; 25°C)
9) Una massa d'acqua, m acqua= 23 l e una massa di vino mvino = 52 l sono a differenti
temperature:Tacqua = 32°C e Tvino = 54°C. Se mescolate insieme, quale temperatura di
equilibrio raggiungono? Per il calore specifico del vino, si prenda: cvino = 3250J/Kg°C
(46; 01°C)
10) Allo scopo di determinare il calore specifico di un metallo, si introduce una massa
m = 100 g di quel metallo, portata alla temperatura di 100°C per immersione in acqua bollente, in
un calorimetro contenente 500 g di acqua alla temperatura di Ta = 20°C. Una volta chiuso il
calorimetro, si attende l'equilibrio, mescolando con un agitatore e si riscontra
Teq = 22C. Quanto vale il calore specifico di quel metallo?( 536; 67 J/Kg°C)
11)Un corpo di rame di massa m=10g e’ riscaldato a 80 °C e immerso in 200 ml di acqua a
temperatura di 18°C dentro un calorimetro. Calcola la temperatura di equilibrio supponendo che la
massa in acqua del calorimetro sia di 12g.
12)Calcola il calore specifico di un corpo di massa 200g riscaldato alla temperatura di 120°C e
immerso in 100ml di acqua a 20°C, sapendo che la massa in acqua del calorimetro e’ di 20g e che
la temperatura di equilibrio e’ 60°C.
13)Un corpo di massa 200g striscia su un piano orizzontale di coefficiente di attrito m=0,2 e si
sposta di 20m. Calcola il lavoro fatto dalla forza di attrito. Se tale energia si dissipa in calore e
viene acquistato interamente dal piano fatto di rame e di massa 10Kg inizialmente alla
temperatura di 18°C, di quanto varia la sua temperatura?
14)Se lo stesso corpo del problema 13) striscia su un piano inclinato di 30° alto 5m, di quanto
varia la temperatura del piano quando il corpo ha percorso l’intero piano? (In entrambi i problemi
si trascuri il calore assorbito dall’aria circostante).
15)Un corpo di rame di massa 200g e temperatura iniziale 20°C viene messo a contatto con un
corpo di alluminio di massa 210g e alla temperatura di 90°C. Se si trascurano le perdite di energia
termica nell’aria, qual e’ la temperatura di equilibrio.
16)Da una altezza di 200m viene lasciata cadere una palla di 200Kg. Cadendo il 20% dell’energia
posseduta viene trasferita al piano su cui cade fatto di rame e di massa 100g che inizialmente si
trova a 20°C. Di quanto varia la temperatura del piano?
17)Un sasso di 0,4 kg cade da un'altezza di 1200m su un contenitore contenente 2,5 kg di acqua.
Di quanto aumenta la temperatura dell'acqua?
18)Un blocco di rame di massa mCu = 300g si trova alla temperatura iniziale TiCu = 90◦C. Un
blocco di alluminio di massa mAl = 700g si trova invece alla temperatura iniziale TiAl = 43◦C. Essi
vengono posti a contatto. Calcolare la temperatura di equilibrio del sistema Teq. (50.3◦C .)
10
19)Due cubetti di rame, ciascuno di massa mCu = 0.2kg e alla temperatura TiCu = 150◦C, vengono
immersi in un recipiente contenente una massa d’acqua mH20 = 1kg alla temperatura iniziale
TiH2O = 30◦C. Sapendo che la temperatura di equilibrio del sistema è Teq = 34.2◦C, calcolare il
calore specifico del rame.( cs rame=380J/kg◦C .)
20)Un calorimetro delle mescolanze contiene 300 g d’acqua alla temperatura iniziale di 18,6 °C. In
esso vengono versati 200 g d’acqua calda, alla temperatura di 72,4 °C. Il sistema raggiunge
l’equilibrio termico alla temperatura di 37,5 °C. Determinare le quantità di calore Q1 e Q2 assorbito
e ceduto dalle due masse d’acqua. Determinare la quantità di calore Qcal assorbita dal
calorimetro. Determinare la massa equivalente del calorimetro
( Q1= 5670 cal; Q2= 6980, come si vede le quantita’ sono diverse e quindi non tutto il calore
ceduto viene acquistato. La differenza e’ disperspa . La massa in acqua equivalente a tale
quantita’ dispersa si ottiene calcolando m dalla legge della calorimetria e si ottiene meq=69,3 g .)
21)Un blocco di ferro di massa 500 g alla temperatura iniziale di 145,0 °C viene immerso in un
calorimetro contenente 280 g d’acqua alla temperatura iniziale di 20,0 °C. Determinare quale
temperatura d’equilibrio raggiungerà il sistema. (calore specifico del ferro: cFe = 452 J/kg·K )
Esercizi sulla teoria dei gas perfetti
Ricordo le unita’ di misura piu’ importanti di pressione:
1Pa=1N/m2
1bar=105 Pa
1 atm=101325 Pa =760 mmHg
1mmHg (chiamato anche “torr” ) =133,322Pa
La relazione tra Unità di massa atomica e mole
La massa dell'atomo, oggetto microscopico della struttura della materia, ha un valore
estremamente piccolo. Le misure eseguite con appositi strumenti hanno portato a stabilire –
attorno al 1960 - che un atomo di 12C – un isotopo del carbonio - ha una massa di
19,926465384 x10-24 g.
Come unita’ di massa atomica si assume la 12esima parte dell’atomo di carbonio 12 (12C)
pari a 1,660538782x10-24 g e si indica con u.m.a
Nella tavola degli elementi compare il numero di massa (anche detto massa atomica e si indica
con M anche se in realta’ non e’ una vera e propria massa ). Tale valore e’ il rapporto tra la vera
massa dell’atomo e l’unita’ di massa atomica. Per l’ossigeno , ad esempio, M=16. Cio’ significa
che la vera massa dell’ossigeno e’ 16x1,660538782x10-24.
11
Massa molecolare e massa molare
La massa della molecola o massa molecolare di un composto chimico è la massa di una
singola molecola di tale composto, espressa in unità di massa atomica (u.m.a). La massa
molecolare può essere calcolata come la somma delle masse atomiche di tutti gli atomi costituenti
la molecola. Il concetto di massa molecolare viene spesso confuso con quello di massa molare.
La mole
La quantità di una sostanza o MOLE è assunta come unità dal Sistema Internazionale e definita
come: quantità di sostanza che contiene tante particelle (atomi, molecole, ioni, ecc., ) quanti
12
sono gli atomi contenuti in 12g di C.
Quanti sono questi atomi?
Per trovare il numero di atomi di carbonio-12 presenti in una mole di carbonio, cioè in 12g di 12C,
basta dividere 12 g per la massa di un singolo atomo di carbonio-12 e pari a 19,92679x10-24 g
atomi
12
C in una mole di
12
C=
12 g / mole
= 6,02204 ⋅ 10 24 atomi
19,92679·10 24 g
Questo numero e’ detto numero di Avogadro e si indica con N0 (oppure anche con NA)
Una mole puo’ anche essere definita come la quantità di sostanza che contiene un numero
di Avogadro di particelle(molecole o atomi)
Per gli atomi la massa molare (espressa in g/mole) e’ il numero di massa (o massa atomica). Per
le molecole la massa molare e’ la somma delle masse molari dei singoli atomi che la
compongono.
Ad esempio: la massa molare dell’ossigeno atomico e’ 16. La massa molare dell’idrogeno e’ 1. La
massa molare della molecola dell’acqua e’ 1+1+16=18 g/mole
Ricordo infine che indichiamo con :
m=la massa in grammi di una certa sostanza ;
M=la massa molare o numero atomico (espressa in grammi/mole)
N=numero di particelle (atomi o molecole presenti in una certa sostanza)
N0=numero di Avogadro cioe’ 6,02204x1024 atomi
n=numero di moli
12
La relazione fra tali grandezze e’:
n=
N
m
; n=
; m = M ⋅ u.m.a
N0
M
Usa la tavola periodica degli elementi per risolvere i problemi seguenti
1)Quante moli di He corrispondono a 300g di He?
2)Quanti atomi sono contenuti in 200g di N?
3)In 300g di O2 quante molecole vi sono?
4)Quante moli corrispondono a 200g di 12C
5)m=200 g di ossigeno atomico a quante moli corrispondono? Quanti atomi contengono?
6)N=23x1045 atomi di idrogeno quante moli sono?
7)L’ossigeno in natura si trova allo stato molecolare e precisamente e’ composto da due atomi di
ossigeno. La molecola di ossigeno si indica con O2. Se si hanno 120g di ossigeno O2, quante moli
sono?, Quante molecole ?
8)L’ozono e’ una molecola composta da 3 atomi di Ossigeno cioè O3 (molto instabile e presente
solo nell’alta atmosfera). 1200 g di O3, quante moli sono, Quante molecole?
Legge di Boyle
9) Alla pressione di 1,8 atm una certa quantità di gas occupa un volume di 0,9 L. Mantenendo
costante la temperatura, la pressione del gas viene portata a 4,1 atm. Calcolare il nuovo volume
occupato dal gas. (0,395 L.)
10) Una certa quantità di gas si trova alla temperatura di 20°C, a 100 mmHg di pressione e
occupa il volume di 0,5 L. Mantenendo costante la temperatura il gas viene compresso sino ad
occupare il volume di 400 mL. Determina la nuova pressione del gas.(125 mmHg.)
11) Di quanti mmHg aumenta la pressione se a temperatura costante un gas che occupa
inizialmente un volume di 3500 mL e si trova alla pressione di 2 atm viene compresso sino ad
occupare un volume di 1,768 L?( 1488,8 mmHg.)
12) Un campione di gas a 25°C e 75 mmHg occupa un volume di 2,20 L. Calcola di quanto si
riduce il volume se il gas viene portato nelle seguenti condizioni sperimentali:
t = 25°C ; P = 0,130 atm.( 0,542 L.)
13
Leggi di Gay-Lussac
13) Mantenendo costante la pressione, 10 L di gas metano vengono riscaldati dalla temperatura di
11°C alla temperatura di 44°C. Quale è il volume finale del gas?( 11,16 L.)
14) Un campione di 25 L di aria viene lasciato espandere a pressione costante fino ad occupare
un volume di 30 L. Se la temperatura finale è 90°C, quale era la temperatura iniziale del gas?
(29,45°C.)
15) Alla temperatura di 18°C un gas occupa il volume di 0,80 L. A P = cost il gas viene raffreddato
sino alla temperatura di -20°C. (695 mL.)
16) Una bombola riempita di elio a 15 atm viene raffreddata da 20°C a -30°C. Determina la
pressione finale del gas in torr assumendo che il volume rimanga costante.(9454,4 torr)
17) Calcola la temperatura assoluta finale di un campione di idrogeno gassoso se 0,7 L di questo
gas a 30°C e 600 mmHg vengono riscaldati finchè la pressione, mantenendo il volume costante,
raggiunge il valore di 780 mmHg.( 395,09 K.)
18) Una bombola in acciaio che contiene una certa quantità di gas si trova inizialmente alla
temperatura di 20°C. La temperatura della bombola viene portata a -50°C; la pressione finale del
gas è di 15,22 atm. Si determini la pressione del gas alla temperatura di 20°C.( 19,99 atm.)
19) Calcolare il volume occupato a 30°C e 1,00·105 Pa da 1,50 moli di O2.( 37,8 cm3.)
20) Un gas che alla temperatura di 25°C e alla pressione di 1,50 atm occupa un volume di 15,0
dm3, viene riscaldato a 60°C. Determinare la pressione del gas sapendo che il suo volume finale
è 15,5 dm3. (0,62 atm.)
21)Un gas ha inizialmente una pressione pari a P0 = 2;3 105 Pa ed un volume di 5 litri. Se
mantenendo costante la temperatura lo si porta alla pressione atmosferica, quale volume andrà ad
occupare?( 11; 35 l)
22)Un gas che alla temperatura T0 = 273K ha un volume pari a V0 = 2m3. Di quanto cambia il suo
volume se viene portato isobaricamente alla temperatura Tf = 300K?( 2;2m3)
23)Una pentola a pressione fa scattare la valvola di sicurezza se, riscaldandola, la pressione al
suo interno raggiunge P = 3 Atm. Supponendo che all'interno della pentola ci sia, inizialmente, del
vapore acqueo in condizioni normali (). Per condizioni normali si intendono i valori P0 = 1 Atm e T0 = 273K
(oppure 0°C), a quale temperatura si trova il vapore quando scatta la valvola? (R: 819,32K)
24)Un gas subisce una trasformazione isocora che lo porta dallo stato A(PA = 1 Atm; TA = 200K)
allo stato B(VB = 5 l; TB = 400K) e successivamente una trasformazione isoterma che lo porta allo
stato C(VC = 8 l). Rappresenta graficamente le due trasformazioni nel piano P-V e calcola il valore
di PC.( 1, 25 Atm)
25)Un gas effettua una trasformazione isoterma AB alla temperatura t = 60°C e successivamente
un'isobara BC. Calcolare la temperatura nello stato C, sapendo che PA = 4 105 Pa, che PB = 1, 5
105 Pa, VA = 7dm3 e VC = 10dm3 (178; 4K)
14
26)Calcolare il volume iniziale di un gas che si trova alla temperatura di 300K e alla pressione di
2Atm, che viene portato ad occupare un volume di 10l alla temperatura di 280K e alla pressione di
2; 5Atm. Il gas risulta compresso o dilatato?( 0; 013m3)
27)n = 2; 5 moli di un gas perfetto, contenute in un volume V = 80 l sono compresse
isotermicamente da uno stato A ad uno stato B, aumentando la pressione da PA = 1; 5 Atm a PB =
1; 8 Atm. Raggiunto lo stato B, si aumenta ancora la pressione mantenendo costante il volume,
sino a giungere alla temperatura TC = 620K. Calcolare la pressione PC.e rappresentare
graficamente le trasformazioni ( 1; 91 Atm)
28)Quale è il volume occupato da 10 g di gas Neon alla temperatura t = 25°C e a pressione 1 atm,
sapendo che la sua massa molare è M(massa molare) = 20, 18 g/mol?
(0;012m3)
29)A quale pressione 4 moli di ossigeno si trovano ad una temperatura t = 25°C in un volume V =
3; 2 l?( 3,097 105 Pa)
30) 3 moli di gas perfetto alla temperatura di TA = 400K e alla pressione di PA = 2; 5 Atm
subiscono un'espansione isoterma AB in modo che nello stato B il volume sia doppio. Il gas è
quindi compresso isobaricamente sino a tornare al volume di partenza. Determina lo stato finale
del gas.(Vc=VA=39l)
31)Rappresenta graficamente nel piano PV le seguenti trasformazioni e calcola per ogni vertice le
coordinate (Pressione, Volume, Temperatura).
Una mole di idrogeno occupa un volume di 0,1 m3 ed e’ alla temperatura di 350K. Viene fatto
espandere a pressione costante e il volume finale raddoppia. Viene fatto espandere a temperatura
costante e la pressione finale e’ la meta’ di quella in A. Gli viene sottratto calore appoggiandolo su
un refrigeratore e mantenedo costante la pressione . Il volume diminuisce fino a quando non
riprende lo stesso valore che aveva in A. Viene infine compresso a volume costante fino a
riportarlo allo stato A. Si e’ compiuto un ciclo simile a quello delle macchine termiche.
32) 3 moli di idrogeno inizialmente alla temperatura di 200K occupano un volume di 0,05m3. Viene
fatto espandere a temperatura costante fino a che il volume e’ di 0,1 m3. Viene quindi compresso
a volume costante . La compressione fa aumentare la temperatura fino a 300K. Quindi viene
compresso a temperatura costante fino a che non ritorna ad avere il volume iniziale. Calcola le
pressioni del gas nei diversi stati finali e disegna nel piano di Clayperon la trasformazione ciclica
subita dal gas.
33)400g di ossigeno O2 si trova inizialmente ad occupare un volume di 0,5 cm3 e una pressione di
0,5 atm. Calcola la temperatura. Il gas viene compresso a volume costante fino alla pressione di 2
atm. Calcola la nuova temperatura e chiediti perché la temperatura e’ aumentata. Nel nuovo stato
il gas viene fatto espandere a pressione costante fino a che non raggiunge un volume di 2 cm3.
Quindi viene fatto espandere a temperatura costante fino a che non ritorna da avere il volume
iniziale. Disegna il ciclo e calcola i dati mancanti (P, V T) in ogni stato del gas.
34)Un gas ha un volume e una pressione iniziale di 3 m3 e di 5 atm. Mantenendo costante la
temperatura quale sarà in suo volume alla pressione di 15 atm? (R: 1m3)
15
35)Un gas occupa un volume di 6,0 L alla temperatura di 60 °C. Sapendo che la pressione iniziale
del gas è di 2,8 atm e che la temperatura non varia, determina la pressione necessaria per portare
il volume a 2,5 L? (R: 6,7atm)
36)Mantenendo la pressione costante, un gas di volume 2,5 dm3 e temperatura iniziale di 26 °C,
viene portato alla temperatura di 80 °C. Quale sarà il volume finale? (R: 3,0 dm3)
37)Un gas subisce una trasformazione a pressione costante a seguito della quale il volume diventa
di 75 L. Sapendo che il volume iniziale alla temperatura di 15 °C era di 32 L, qual è la temperatura
raggiunta? (R: 409 °C)
38)Un gas, contenuto in una bombola, ha una pressione di 4,6 atm a temperatura ambiente (20
°C). Portando il gas alla temperatura di -30 °C, qual è la pressione raggiunta? (R:3,8 atm)
39)Un recipiente chiuso contiene aria a 2,5 atm alla temperatura di 100 °C. Determina la
temperatura dell'aria quando raffreddando il recipiente la pressione scende a 1,5 atm. (R: -45 °C)
40)Una bombola di capacità pari a 0,030 m3 contenente 10 moli di ossigeno alla temperatura T =
313 K. Qual è la pressione? (R: 8,67•105Pa)
41)Un bidone per petrolio contenente soltanto aria viene chiuso ermeticamente a 20 °C. Poi viene
collocato al sole, ove si riscalda fino a raggiungere la temperatura di 60 °C. Se la pressione
iniziale, nell’interno del bidone, è 1 atm, quale sarà la pressione finale? Assumere che il volume
del bidone rimanga costante, mentre varia la temperatura. (R: 1.1atm)
42)Un manometro fornisce un valore pari a 190 kPa per le gomme di un’auto, in una giornata nella
quale la temperatura è – 10 °C e la pressione barometrica è 800 torr. Che valore segnerà il
manometro, dopo che l’automobile ha viaggiato e la temperatura degli pneumatici (compresa l’aria
all’interno) ha raggiunto i 35 °C? Assumere che il volume delle gomme non subisca modifiche.
(R: 241 kPa)
Quesiti
1)Se un gas ideale mantenuto a temperatura
costante triplica il suo volume, la pressione finale,
rispetto a quella iniziale risulta:
a. la stessa.
b. triplicata.
c. ridotta a 1/3.
d. nove volte maggiore.
2)Supponendo che l’aria contenuta in una stanza
sia assimilabile a un gas perfetto, che cosa è
necessario misurare per poter valutare il numero
di molecole presenti?
a. Volume, temperatura, pressione.
b. Pressione, quantità di calore scambiata.
c. Temperatura, volume.
d. Volume, temperatura, calore.
16
3)Qual è la pressione cui si trova una mole di gas
perfetto contenuto in un recipiente di 10 dm3
alla temperatura di 100 K?
a. 83.2 pascal c. 8320 pascal
b. 832 pascal d. 83 200 pascal
4)Una bombola da 20 litri contiene aria alla pressione
di 1 atm a 0 °C. Sapendo che la densità
dell’aria è 1.29 kg/m3, a quelle condizioni,
quale sarà la sua densità se la temperatura è
portata a 100 °C?
a. 0.94 kg/m3 c. 1.77 kg/m3
b. 1.29 kg/m3 d. 1.77 g/m3
5)Per quali leggi è possibile, senza particolari
accorgimenti, usare per la pressione valori
espressi in atmosfere invece che in pascal?
a. Legge di Boyle.
b. Legge dei gas perfetti.
c. Legge di Charles.
d. Legge zero della termodinamica.
6)Se 14.0 mg di azoto gassoso (M = 28.0 kg/kmol) sono tenuti a 27.0 °C in un contenitore avente
un volume pari a 5.00 × 103 cm3, quale sarà la pressione del gas nell’interno del contenitore?
7)Che valore ha la massa di un singolo atomo di (a) oro, (b) argento,(c) ferro?
8)La formula chimica per l’ammoniaca gassosa è NH3. Qual è la massa di una molecola di
ammoniaca?
9)Il benzene ha la formula chimica C6H6. Quante molecole di benzene sono contenute in un
campione di 50 g?
10)Quanti atomi sono presenti in un pezzo di rame puro la cui massa è pari a 20 g?
11)Un bicchiere contiene 80 g di acqua pura. Quante molecole d’acqua si trovano dentro il
bicchiere? La formula chimica dell’acqua è H2O.
12)Una bombola da 1 litro contiene ossigeno O2 a 22 °C e ad una pressione relativa pari a 2.2 ×
106 Pa. Che massa di ossigeno è contenuta nella bombola?
13)Una bombola da 2 litri contiene elio gassoso (He) a 33 °C e 1200 kPa. Che massa di elio è
contenuta nella bombola?
14)Un gas a temperatura ambiente (27 °C) e alla pressione atmosferica di 100 kPa viene
compresso fino a un volume pari a un decimo del suo volume originario e ad una pressione
assoluta pari a 2500 kPa. Qual è la nuova temperatura del gas?
15)La pressione di un gas in un serbatoio si triplica quando il suo volume viene dimezzato.
Calcolare il rapporto tra la temperatura finale e quella iniziale del gas.
17
16)Un serbatoio contiene una mole di ossigeno gassoso a una pressione assoluta pari a 500 kPa
e alla temperatura di 27 °C.
(a) Se il gas viene riscaldato, mantenendo il volume costante, fino a quadruplicare la pressione
rispetto al valore originario, qual è la nuova temperatura del gas?
(b) Se il gas viene riscaldato fino a raddoppiarne sia il volume sia la pressione, qual è la
nuova temperatura del gas?
17)Una bombola contiene ossigeno alla temperatura di 27°C e alla pressione di 2,0 x 10^5 N/m^2.
Sapendo che la bombola può sopportare una pressione massima pari a 6,0 x 10^5 N/m^2, fino a
quale temperatura si può riscaldare il gas?
18)Che cosa si intende per gas ideale? Rispondi in cinque righe.
19)Mantenendo costanti la temperatura e il numero di moli, se si dimezza il volume di un certo
campione di gas
a) si dimezza la pressione
b) si dimezza la densità
c) si raddoppia la pressione
d) si dimezza il numero di molecole
20)Un gas viene compresso a temperatura costante fino a occupare metà del suo volume iniziale.
Come varia la pressione?
21)Un cilindro con un pistone ha un volume di 250 mL e contiene un gas alla pressione di 1,00
atm e alla temperatura di 25 °C. Estrai il pistone fino a portare il volume a 750 mL senza variare la
temperatura. Calcola il nuovo valore della pressione
22)Un campione di 100 mL di gas è contenuto in un cilindro alla pressione di 101 kPa. Calcola il
volume del gas a 202 kPa e alla stessa temperatura.
23)Per dimostrare che la fermentazione alcolica effettuata dal lievito di birra produce CO2 si
monta un apparecchio che raccoglie il gas prodotto. Viene misurato un volume di 15 mL alla
pressione di 1,0 atm e a temperatura ambiente. Il gas viene poi convogliato in un contenitore da
10 mL. Qual è il valore della pressione finale se la temperatura non è variata?
24)Un gas ha un volume di 70 dm3 a 30 °C e 1,0 atm. Qual è il volume finale espresso in litri se la
temperatura scende a 10 °C e la pressione rimane costante?
25)Un gas si trova a 150 °C e occupa il volume di 1,00 L. Dimezzando il volume a pressione
costante, quale sarà la sua temperatura in kelvin?
26)Calcola il volume finale di un campione gassoso di 200 mL riscaldato da 20 °C a 300 °C a
pressione costante.
27)Un campione di neon occupa un volume di 400 mL alla temperatura di 200 °C. Quale sarà il
suo volume a 0 °C, mantenendo costante la pressione?
28)In seguito a riscaldamento, un gas aumenta il suo volume da 2,00 dm3 a 8,00 dm3. Calcola la
temperatura finale sapendo che quella iniziale era di 30 °C.
29)A quale temperatura una massa di elio occuperà il volume di 10,8 dm3, se a 12 °C possiede un
volume di 10,0 dm3?
18
30)Definisci che cosa si intende per zero assoluto.
31)Perché è una condizione che non può essere raggiunta utilizzando un normale gas come, per
esempio, l’ossigeno? Rispondi in sei righe.
32)Se una massa di gas mantiene la pressione costante, ma varia la sua temperatura da 15 °C
a -20 °C, che cosa accade al volume che occupa?
33)Un gas occupa un volume di 500 mL e si trova alla temperatura di 25 °C e 1,00 atm. La
pressione viene ridotta a 0,700 atm e il gas subisce un’espansione. .Calcola a quale temperatura
è necessario portare il gas, mantenendo costante la pressione, per ottenere la stessa
temperatura.
34)Due recipienti chiusi contengono rispettivamente idrogeno e ossigeno alle stesse condizioni di
temperatura e pressione. Come varia la temperatura se i gas sono sottoposti a un aumento della
pressione?
a) resta costante
b) aumenta
c) diminuisce
d) raddoppia
35)Una massa di idrogeno e una di ossigeno sono contenute in due recipienti chiusi
rispettivamente alla pressione di 780 mmHg e 0,950 atm. Essi vengono riscaldati fino a 30 °C e
compressi fino a 2,00 atm.. Calcola la temperatura iniziale dei due gas espressa in kelvin.
36)Una bombola che può sopportare una pressione di 4,30 atm viene riempita di gas alla
pressione di
3,00 atm e alla temperatura di 25 °C. Al di sotto di quale temperatura dovrà essere mantenuta la
bombola per evitarne l’esplosione?
37)Sulle bombolette spray è riportata la norma di non esporle a temperature superiori a 50 °C.
Se la pressione interna a 25 °C è di 1,5 atm, quale valore assume la pressione a 50 °C?
38)Un gas ha una pressione di 0,7 kPa e una temperatura di 20 °C. A volume costante, il gas
viene raffreddato a –10 °C. Qual è la pressione finale?
39)Calcola la temperatura a cui si deve portare un gas, a volume costante, in modo tale che la
pressione finale sia il doppio della pressione p0 °C.
40)Una bombola che contiene un campione di gas è dotata di una valvola che resiste alla
pressione di 3 atm.
41)Traccia il grafico della pressione in funzione della temperatura sapendo che quando t1 = 0 °C
si ha p1 = 1,0 atm e che per t2 = 82 °C si ha p2 = 1,3 atm.
a)Determina per via grafica a quale temperatura la pressione ha un valore di 2,2 atm.
b)Determina, sempre per via grafica, a quale pressione la temperatura raggiunge i 50 °C.
c)A quale temperatura si aprirà la valvola della bombola?
43)Qual è la definizione del principio di Avogadro?
19
Quante moli di H2 sono contenute in un cilindro di 50 L alla pressione di 10 atm e alla temperatura
di 27 °C?
44)Calcola il numero di moli di gas contenuto in un recipiente di 35 L a 151 °C e 2,0 atm.
45)Calcola il volume di elio occupato da 3,0 mol a 400 °C e 3,0 mmHg.
46)Un gas viene raffreddato da 35 °C a –5 °C . Sapendo che il volume e la pressione iniziale
erano 200 L e 8,0 atm, calcola qual è il volume finale se la pressione è scesa fino 0,50 atm.
20












