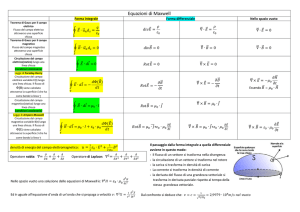
Dopo aver definito il <<Flusso di un Campo vettoriale attraverso una superficie
(piana o chiusa)>> e la <<Circuitazione di un Campo vettoriale lungo una linea
chiusa>>, evidenziare come essi rappresentano gli strumenti concettuali e
operativi che permettono di descrivere il comportamento dei campi elettrici e
magnetici , nonché le loro reciproche interazioni ( Max . 30 righe + eventuali
figure)
Il flusso di un vettore
attraverso una superficie piana di area S è un’operazione matematica data dal
prodotto scalare del vettore con il vettore
, dove è il versore normale, ovvero il il vettore
di modulo unitario,perpendicolare alla superficie e diretto fuori dalla pagina che si considera. In
formule:
dove è l’angolo compreso tra
(Fig.1)
Per calcolare il flusso attraverso una superficie chiusa si divide la superficie in elementi dS tanto piccoli
da poter essere considerati piani e si sommano tutti i dΦ dell'intera superficie
In particolare il flusso del vettore campo elettrico
( o del vettore campo magnetico
, il flusso è
direttamente proporzionale al numero delle linee di forza che attraversano la superficie. Se la superficie è
chiusa vale il Teorema di Gauss :
Il flusso del vettore
attraverso una superficie chiusa, non
dipende dalla superficie, ma è uguale alla somma algebrica delle cariche interne e inversamente
proporzionale alla costante dielettrica del mezzo.Il flusso del vettore attraverso una superficie chiusa è
sempre nullo.
Da queste relazioni si deduce che le linee di forza di
sono linee aperte cioè hanno sorgenti (cariche
positive) e pozzi (cariche negative), mentre le linee di forza di
sono linee chiuse e non esistono poli
magnetici isolati. Per il campo elettrico si deduce anche la legge dell’inverso del quadrato della distanza
(legge di Coulomb)
Sia
un campo vettoriale ed L una linea chiusa (orientata) . Si suddivide L in n porzioni
abbastanza piccole da essere considerate segmenti orientati o vettori e si calcola per ciascun elemento di
linea il prodotto scalare
, dove rappresenta il campo presente nel tratto
Si definisce Circuitazione del campo vettoriale
e si indica con C(
,la somma
(Fig.2)
In particolare se la circuitazione è nulla lungo qualsiasi linea chiusa il campo è conservativo ( come
il campo elettrostatico. (
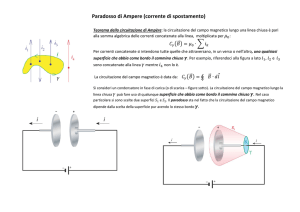
ha per significato fisico una differenza di potenziale) Nel caso del vettore
campo magnetico,la circuitazione calcolata lungo una linea di forza è uguale a
,
, dove i rappresenta la
risultante delle correnti concatenate alla linea chiusa.
Queste relazioni diventano strumento operativo in quanto permettono di calcolare il valore di
E o di B, note le sorgenti del campo.
Maxwell ha poi sintetizzato , nella terza e nella quarta equazione , le interazioni tra Campo
elettrico e campo magnetico ::un campo magnetico variabile genera un campo elettrico la cui circuitazione
è
, mentre un campo elettrico variabile genera un campo magnetico tale che
In particolare la terza equazione afferma che , in presenza di campi magnetici variabili
non è nulla e rappresenta la forza elettromotrice indotta
Fig.1
Fig. 2