Enuncia e commenta i postulati proposti da Einstein sulla relatività ristretta.
La luce è una particolare onda trasversale che si può propagare nel vuoto. Si tratta di
un’onda elettromagnetica che ha, nel vuoto, la sua velocità massima c pari a circa
300.000 km/s. Questo valore, nella teoria dell’elettromagnetismo, è lo stesso in tutti i
sistemi di riferimento, qualunque sia la loro velocità relativa rispetto all’osservatore e si
dice, perciò, che è una grandezza invariante. Questo è in disaccordo con le previsioni della
meccanica classica e, in particolare, con le trasformazioni di Galileo che affermano che la
velocità della luce deve variare, da un sistema di riferimento ad un altro, così come varia la
velocità di ogni corpo. Proprio per risolvere questa contraddizione tra meccanica ed
elettromagnetismo, Einstein propone due assiomi. Il primo, chiamato principio di
relatività ristretta o speciale, afferma che le leggi della Fisica hanno la stessa forma in tutti
i sistemi fisici inerziali e non esiste quindi un riferimento privilegiato. Il secondo assioma,
chiamato principio di invarianza di c, afferma invece che la velocità della luce è la stessa in
tutte le direzioni e in tutti i sistemi di riferimento inerziali, indipendentemente dal moto
del sistema stesso o della sorgente da cui la luce è emessa.
Descrivi il funzionamento di un trasformatore
Il trasformatore è una macchina elettrica definita statica perché non contiene parti in
movimento. Il trasformatore consente di innalzare ed abbassare, in maniera efficiente e
senza eccessive perdite, il valore della tensione e corrente in ingresso rispetto a quelli in
uscita. Un trasformatore può essere costituito da due solenoidi, avvolti su un anello di
materiale ferromagnetico detto nucleo magnetico. L’avvolgimento al quale viene fornita
energia viene detto primario, mentre quello dalla quale l’energia è prelevata è detto
secondario. Quando sul primario viene applicata una tensione elettrica alternata
sinusoidale, per effetto dell’induzione magnetica, si crea nel nucleo un flusso magnetico
con andamento sinusoidale. Per la legge di Faraday-Neumann-Lenz, questo flusso
variabile induce nel secondario una tensione sinusoidale, che si può dimostrare essere
proporzionale al rapporto tra il numero di spire del primario e quelle del secondario.
Descrivi i fenomeni di autoinduzione e mutua induzione
L’autoinduzione è un fenomeno fisico che avviene ogni volta che la corrente in un circuito
elettrico varia nel tempo. Se la corrente, ad esempio, aumenta rapidamente, si genera un
flusso magnetico che varia rapidamente come la corrente attraverso la superficie del
circuito. Questo induce un’altra corrente nel circuito che ha verso opposto alla prima e che
tende a stabilizzare il flusso totale. Il fenomeno della mutua induzione riguarda invece due
circuiti elettricamente separati posti in prossimità l’uno dell’altro. Nel caso in cui si abbia
una variazione di corrente in uno dei due circuiti, si avrà una variazione di flusso anche nel
secondo circuito e quindi si genererà, all’interno di quest’ultimo, una corrente elettrica. I
fenomeni dell’autoinduzione e della mutua induzione vengono utilizzati nei trasformatori
elettrici.
Illustra brevemente il concetto di simultaneità secondo Einstein e le sue
conseguenze.
RISPOSTA
Einstein dà una definizione operativa di simultaneità di due eventi: due eventi sono
simultanei se posso osservare la luce che essi emettono arrivare contemporaneamente in
un
punto
equidistante
dai
punti
in
cui
si
sono
verificati.
A partire da questa definizione, la simultaneità dei due eventi è relativa al sistema di
riferimento da cui si osserva: se ad esempio due lampi emessi da due fari posti sul terreno
sono ricevuti nello stesso istante da un osservatore fermo rispetto a essi, un osservatore
che si stia muovendo sulla linea che congiunge i due faretti non osserverà i due lampi
contemporaneamente, perché nel tempo che la luce impiega a raggiungerlo egli si sarà
avvicinato a uno e allontanato dall’altro. Questo tipo di considerazioni hanno portato
Einstein a formulare successivamente la teoria della relatività.
Visualizza risposta
Domanda 12
Su quali presupposti teorici Einstein ha sviluppato la teoria della relatività?
RISPOSTA
Einstein assume come postulato la velocità c della luce costante in tutti i sistemi di
riferimento inerziali, come descritta dalle equazioni di Maxwell. Estende dunque il principio
di relatività galileiano, che afferma che le leggi fisiche devono avere la stessa forma in tutti
i sistemi di riferimento inerziali, in modo da includere la costanza di c. Le leggi di
trasformazione da un sistema di riferimento inerziale a un’altro saranno dunque descritte
dalle trasformazioni di Lorentz, in cui le velocità si compongono in modo da mantenere
costante c, al contrario delle trasformazioni di Galilei.
Visualizza risposta
Domanda 13
Illustra brevemente l’esperimento di Michelson e Morley e discutine l'importanza.
RISPOSTA
L’esperimento di Michelson e Morley aveva lo scopo di dimostrare l’esistenza dell’etere,
una sostanza impalpabile in cui si sarebbero propagate le onde elettromagnetiche,
ipotizzata per giustificare il carattere invariante della loro velocità previsto dalle equazioni
di Maxwell.
L’idea era dunque quella di osservare gli effetti della differenza di tempo impiegata a
percorrere la stessa distanza da due fasci di luce su cammini tra loro perpendicolari, di cui
uno parallelo al moto della terra nell’etere e l’altro perpendicolare ad esso. Questa
differenza di tempi avrebbe dovuto produrre le caratteristiche figure di interferenza in un
interferometro appositamente costruito.
Tale interferenza non si osservò, e l’esperimento costrinse ad accantonare l’ipotesi
dell’etere, e a cercare altre ipotesi per spiegare la costanza della velocità, preparando il
terreno alla teoria della relatività ristretta di Einstein.
Visualizza risposta
Trattazione sintetica (in 20 righe)
L’energia potenziale del campo elettrico in un punto è il lavoro che la forza elettrica deve
compiere per spostare una carica da quel punto all’infinito, cioè al limite del campo. Il lavoro della
forza elettrica che, essendo conservativa, dipende solo dalla posizione iniziale A e da quella finale
B è pari a KQq (1/RA – 1/RB). Ponendo il punto B ai limiti del campo, cioè facendo tendere R B
all’infinito, otteniamo che il lavoro della forza elettrica per spostare la carica dal punto A all’infinito
è KQq/RA, che per definizione è l’energia potenziale nel punto A.
Come si può osservare, l’energia potenziale è legata alla carica posta nel punto A. Si introduce
perciò il concetto di potenziale (V): questo è una grandezza scalare legata solo alle caratteristiche
del campo e pari a U/q, quindi KQ/RA. Per differenza di potenziale si intende proprio la differenza
tra i valori dei potenziali in due punti del campo e serve per stabilire verso quale dei due si muoverà
la carica, ricordando che il vettore campo elettrico punta sempre verso i punti a minore potenziale.
Punti che si trovano alla stessa distanza dalla carica generatrice, ovvero con R uguale, hanno una
d.d.p. pari a zero e sono quindi su superfici equipotenziali. La d.d.p. è legata al lavoro della forza
elettrica dalla seguente relazione L = q .( VA-VB), che deriva dal fatto che per le forze conservative
L = -U = UA-UB = q VA-qVB Prendendo q a fattor comune nella relazione precedente ottengo la
suddetta relazione.
Osservazione : il lavoro della forza elettrica , nel caso in cui q sia positiva, è positivo, nullo,
negativo a seconda che risulti VA>,=,<VB ( il contrario se q è negativa)
Il teorema di Gauss afferma che il flusso del campo elettrico attraverso una superficie chiusa è
uguale al rapporto tra la somma algebrica delle cariche presenti al suo interno e la costante
dielettrica del mezzo. Questo vuol dire che non sono rilevanti né l’area della superficie, né la
distanza da questa, né le cariche esterne le quali generano un flusso prima negativo e poi positivo
attraverso la superficie ( o viceversa ).
Una superficie chiusa di questo tipo viene chiamata gaussiana ed è usata per la determinazione del
campo elettrico generato da una distribuzione continua di cariche, come ad esempio da un
conduttore sferico di raggio R, che genera un campo radiale al suo esterno ( mentre all’interno è
nullo , come per qualsiasi conduttore)
Si fissa un punto a distanza r>R dal centro del conduttore e si sceglie una superficie gaussiana che
per comodità prenderemo come una sfera di raggio r ,concentrica, che contenga la sfera conduttrice.
A questo punto il flusso è sia pari a E . S ( ** noi vogliamo determinare il campo in un
determinato punto a distanza r dal centro del conduttore, supponendo che sia radiale, non
uniforme** il campo con E supposto costante perché siamo in prossimità della sfera) e sia a Q/0
per il teorema di Gauss. Essendo S = 4 r2 otteniamo che
E = Q / 4 r2 0 :
ovvero il campo si calcola come se la carica fosse concentrata tutta nel centro del conduttore .
Un discorso analogo si può fare per una distribuzione di cariche su una lastra piana. In questo caso
il campo si può considerare costante in prossimità della superficie e anche perpendicolare ad essa.
Una comoda superficie gaussiana è quella cilindrica, poiché lungo la sua superficie laterale il flusso
è nullo e perciò rimane da considerare solo quello attraverso le due basi. Il flusso sarà quindi pari
sia a 2 E . S (essendo due le basi) e poi, per il teorema di Gauss , a S / 0. Uguagliando le due
espressioni ottengo che E = 0.
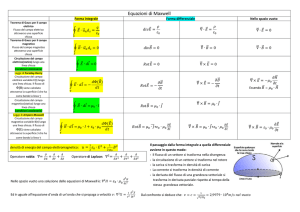
Dopo aver definito il <<Flusso di un Campo vettoriale attraverso una superficie (piana o
chiusa)>> e la <<Circuitazione di un Campo vettoriale lungo una linea chiusa>>,
evidenziare come essi rappresentano gli strumenti concettuali e operativi che permettono di
descrivere il comportamento dei campi elettrici e magnetici , nonché le loro reciproche
interazioni ( Max . 30 righe + eventuali figure)
Il flusso di un vettore
attraverso una superficie piana di area S è un’operazione matematica
data dal prodotto scalare del vettore con il vettore
, dove è il versore normale, ovvero
il il vettore di modulo unitario,perpendicolare alla superficie e diretto fuori dalla pagina che si
considera. In formule:
dove è l’angolo compreso tra
(Fig.1)
Per calcolare il flusso attraverso una superficie chiusa si divide la superficie in elementi dS tanto
piccoli da poter essere considerati piani e si sommano tutti i dΦ dell'intera superficie
In particolare il flusso del vettore campo elettrico ( o del vettore campo magnetico , il flusso è
direttamente proporzionale al numero delle linee di forza che attraversano la superficie. Se la
superficie è chiusa vale il Teorema di Gauss :
Il flusso del vettore
attraverso una
superficie chiusa, non dipende dalla superficie, ma è uguale alla somma algebrica delle cariche
interne e inversamente proporzionale alla costante dielettrica del mezzo.Il flusso del vettore
attraverso una superficie chiusa è sempre nullo.
Da queste relazioni si deduce che le linee di forza di sono linee aperte cioè hanno sorgenti
(cariche positive) e pozzi (cariche negative), mentre le linee di forza di sono linee chiuse e non
esistono poli magnetici isolati. Per il campo elettrico si deduce anche la legge dell’inverso del
quadrato della distanza (legge di Coulomb)
Sia
un campo vettoriale ed L una linea chiusa (orientata) . Si suddivide L in n porzioni
abbastanza piccole da essere considerate segmenti orientati o vettori e si calcola per ciascun
elemento di linea il prodotto scalare
, dove rappresenta il campo presente nel tratto
Si definisce Circuitazione del campo vettoriale
e si indica con
C(
,la somma
(Fig.2)
In particolare se la circuitazione è nulla lungo qualsiasi linea chiusa il campo è conservativo ( come
il campo elettrostatico. (
ha per significato fisico una differenza di potenziale) Nel caso del
vettore , campo magnetico,la circuitazione calcolata lungo una linea di forza è uguale a
, dove
i rappresenta la risultante delle correnti concatenate alla linea chiusa.
Queste relazioni diventano strumento operativo in quanto permettono di calcolare il valore
di E o di B, note le sorgenti del campo.
Maxwell ha poi sintetizzato , nella terza e nella quarta equazione , le interazioni tra Campo
elettrico e campo magnetico ::un campo magnetico variabile genera un campo elettrico la cui
circuitazione è
, mentre un campo elettrico variabile genera un campo magnetico
tale che
In particolare la terza equazione afferma che , in presenza di campi magnetici variabili
non è nulla e rappresenta la forza elettromotrice indotta
Fig.1
Fig. 2
Le trasformazioni di Lorentz, che prendono il nome dal loro principale scopritore, il fisico e
matematico, furono inizialmente introdotte per rimuovere le contraddizioni esistenti tra
elettromagnetismo e meccanica classica. Sotto di esse le equazioni dell'elettromagnetismo
rimangono invarianti nel passaggio tra due sistemi di riferimento in moto relativo tra loro.
Le trasformazioni di Lorentz sono alla base della formulazione matematica della teoria
della
relatività
ristretta
(o
speciale)
di
Einstein.
Le trasformazioni delle coordinate di Lorentz per due sistemi di riferimento inerziali S e S',
con S' che si muove con velocità costante v rispetto a S, e del vettore velocità u di un
corpo parallelo agli assi coincidenti x e x' sono
Fonte: trasformazioni di lorentz
l fenomeno dell’induzione elettrostatica può essere verificato utilizzando un elettroscopio a
foglie. In questo caso l’elettroscopio non viene toccato ma semplicemente si avvicina un
oggetto carico positivamente le cariche negative dell’elettroscopio si radunano verso
l’oggetto positivo mentre l’altra parte dell’elettroscopio si carica positivamente e le lamelle
si respingono.
In questo caso il fenomeno sparisce allontanando l’oggetto carico.
Dal punto di vista microscopico il campo generato dalle cariche positive del corpo che si
avvicina ha reso l’elettroscopio neutro un dipolo elettrico infatti pur essendo rimasta
inalterata la carica neutra dell’elettroscopio lo spostamento delle cariche negative verso il
corpo carico ha reso diverso il centro delle cariche negative da quelle positive.
Questo ha generato un momento di dipolo elettrico indotto.
Con questo meccanismo si spiega anche perché un corpo elettrizzato attrae dei piccoli
pezzi di carta. Pur essendoci una quantità enorme di elettroni lo spostamento degli
elettroni ad un ceto punto si ferma perché il campo positivo generato dall’altra parte del
dipolo eguaglia il campo esterno.
La circuitazione del campo elettrico è il calcolo dell’integrale di E in dl. Per comprendere il
significato di tale integrale supponiamo di avere un campo generato da una carica
puntiforme, esso sarà radiale e scegliamo un percorso che abbia due lati su due raggi e
due su archi di curva circolari in modo da tornare nel punto di partenza. Il lavoro svolto per
spostare una carica sugli archi di curva circolare è 0 in quanto sono curve equipotenziali,
invece sui raggi il lavoro sarà W=E*∆R dove cosx è 1 e sarà di segno opposto tra
avvicinamento e allontanamento. Pertanto in totale il lavoro sarà nullo su una superficie
chiusa. I campi di forze per i quali vale tale calcolo è detto conservativo (come quello
gravitazionale). Il calcolo fatto dipende ovviamente dal percorso scelto ma è possibile
dimostrare che rimane vero per qualsiasi curva (si tenga conto che il calcolo è un prodotto
scalare e che quindi conta solo la parte del percorso per il cosx angolo tra campo e
percorso. L’analogia tra il campo elettrico e quello gravitazionale è relativa alla dipendenza
delle relative forze dall’inverso del quadrato delle distanze che è caratteristica dei campi
conservativi.
Spiega brevemente la nascita della teoria della relatività
Da galilei e passando per Newton le leggi della fisica hanno la stessa forma in tutti i
sistemi spazio temporali in moto relativo rettilineo uniforme. Tali sistemi sono sistemi in cui
valgono le regole della geometria euclidea e nei quali è possibile stabilire un tempo
universale. In tali sistemi la trasformazione delle leggi fisiche lascia la forma inalterata
delle stesse, gli oggetti hanno sempre le stesse dimensioni le accelerazioni sono uguali in
tutti
i
sistemi.
Con gli studi sull’elettromagnetismo nacquero i primi problemi, infatti già la la legge di
Lorentz non risultava covariante né invariante per cambiamento di sistema di riferimento.
Dopo varie proposte tipo la presenza di un mezzo particolare nel quale viaggiassero le
onde elettromagnetiche,l’etere, che con l’esperimento di Michelsohn fu dimostrato non
essere reale, Einstein propose la relatività ristretta che si basava su alcuni principi:
a) indistinguibilità di sistemi di riferimento inerziali
b) costanza della velocità della luce in qualunque sistema.
Da questo deriva che il concetto di simultaneità è relativo e che lo spazio e il tempo si
trasformano con le trasformazioni di Lorentz, quindi le lunghezze e il tempo nei sistemi in
moto relativo non sono uguali. Tutte le leggi della meccanica andavano riscritte valendo la
vecchia meccanica solo per velocità piccole rispetto a quella della luce.
1) Calcola il raggio r e la velocità angolare om della traiettoria circolare che compie una
particella di massa m e carica q quando entra con velocità v all’interno di un campo
magnetico B perpendicolarmente alle linee di forza.
Una particella carica che si muove in un campo magnetico è soggetta alla forza di Lorentz:
F=qvxB
in modulo: F = q v B sin beta = q v B
essendo beta pari a 90°, poiché v perpendicolare a B.
Essendo F sempre perpendicolare a v (per il prodotto vettoriale) la traiettoria sarà un
MCU. Per la 2° legge della dinamica:
F=ma
avremo: q v B = m v^2/r
dove v^2/r è l’accelerazione centripeta.
Semplificando v ed esplicitando r avremo:
r = m v/q B
Se per l’accelerazione centripetà utilizziamo l’altra formula om^2 r si può ottenere:
q (om r) B = m om^2 r
da cui: om = q B / m
2) Spiega come Maxwell deduce la formula della corrente di spostamento nel teorema
della circuitazione del campo magnetico e scrivi la formula finale della 4° equazione di
Maxwell.
3) Calcola l’espressione matematica della forza elettromotrice indotta generata da una
spira che ruota con velocità angolare costante all’interno di un campo magnetico
(alternatore).
4) Scrivi l’equazione della maglia in un circuito RL, l’espressione della funzione che
rappresenta l’andamento della corrente dopo la chiusura dell’interruttore e verifica per
sostituzione che i(t) è effettivamente soluzione dell’equazione differenziale della maglia.