Weekly Summary (2)
• Centro di massa e baricentro
• Momenti di forza, momenti di inerzia e moto rotatorio
• Equilibrio di un corpo rigido
• Le leve • Elasticità, trazione, torsione e fratture ossee
• Esercizi sulle articolazioni
Lezione (4) 9/10/11
Statica
La statica studia come i corpi rigidi ed estesi
stanno in equilibrio. Molto spesso questa
condizione è difficile da raggiungere, come
dimostra la fotografia del ginnasta!
È facile trovare degli esempi in cui un
oggetto non si muove perché la somma delle
forze agenti sull’oggetto è nulla: un libro su
un tavolo
Prima condizione di equilibrio:
!
! Fi = 0
Coppia di forze
È però possibile trovare dei casi in cui, nonostante la prima condizione
sia soddisfatta, un oggetto si muove:
Coppia di forze: 2 forze uguali in
modulo e direzione ma verso opposto,
prima condizione soddisfatta ma il
corpo ruota!
La prima condizione non è sufficiente
per l’equilibrio di corpi rigidi che
possono ruotare!
"F = 0
i
Cosa permette agli oggetti di ruotare?
Momento di una forza
Quando abbiamo un corpo vincolato
a ruotare attorno a un asse occorre
introdurre il momento di una forza Μ
!
FC
Prodotto vettore tra due vettori!
!
!
FD
!
! !
M A = rA " FA
ra=braccio della forza Fa
Prodotto tra rA e la componente
della forza perpendicolare
!
(in questo caso FA). • FA e FC danno lo stesso momento
!
• FD da momento nullo, forza parallela al braccio
• FA è più efficace di FB perché il braccio è più lungo
Il segno del vettore Ma si trova con la regola della mano destra!
Oppure: sento antiorario, positivo; senso orario, negativo
!
FB
Equilibrio dei corpi rigidi
La seconda condizione di equilibrio
per i corpi rigidi è la somma dei
momenti nulla:
!
"M = 0
In questo specifico caso la
seconda condizione di
equilibrio si scrive
!
!
!
Ma + Mb = 0
! ! ! !
ra ! Fa " rb ! Fb = 0
E per annullare il momento Ma posso:
1. Usare una forza uguale e opposta con lo stesso braccio ra
2. Usare una forza maggiore con braccio minore rb
Centro di Massa
Per introdurre il centro di massa possiamo
pensare a un’asta alle cui estremità ci sono 2
sfere di massa diversa. Il sistema deve essere
rigido!
In fisica è importante trovare le coordinate
del centro di massa, definito come:
rCM =
m1r1 + m2 r2 m1r1 + m2 r2
=
m1 + m2
M
Quando abbiamo un corpo rigido occorre
utilizzare l’integrale:
rCM
r dm ! d(r)r dV
!
=
=
M
M
Significato del Centro di Massa
Matematicamente si chiama la media pesata delle
distanze rispetto alle masse.
Per il sistema a due corpi in figura il punto medio
si trova al centro dell’asta, se pesiamo rispetto alle
masse il centro (di massa) si trova vicino alla massa
più grande: come dice la parola è un punto che ci
dice mediamente dove si trova concentrata la
massa.
È importante per due motivi:
1. è possibile scrivere le equazioni del moto,
seconda legge della dinamica, utilizzando le
coordinate del centro di massa!
2. rappresenta il punto in cui un sistema può
essere posto in equilibrio in un campo
gravitazionale costante (si parla anche di
baricentro) Seconda legge della dinamica
F1 = m1a1; F2 = m2 a2
F1 + F2 = m1a1 + m2 a2
FEXT
Sommiamo membro a membro
mi!!
ri
= ! mi ai = ! mi!!
ri = M !
= M!!
rCM
M
i
i
FEXT = MaCM
Possiamo scrivere, come per un punto materiale, la seconda legge
della dinamica sostituendo alla massa la massa totale, alla forza le
forze esterne e all’accelerazione quella del suo centro di massa.
Un corpo rigido si muove sotto l’azione di forze esterne come se
tutta la massa fosse concentrata nel suo centro di massa.
Esempi
La tuffatrice si muove lungo una
traiettoria parabolica sia quando
sta in posizione eretta che quando
ruota: la traiettoria del centro di
massa dipende dalle forze esterne,
qui la forza di gravità. Il CM è
all’altezza dell’ombelico. La
traiettoria parabolica è quella di un
oggetto lanciato verso l’alto.
Perché nel salto in alto (con o
senza asta) si usa questa tecnica?
Pensate alla posizione del CM!
Moti rotatori
Il momento di una forza è ciò che mette in rotazione un corpo. Cosa
caratterizza la rotazione di un corpo?
Occorre introdurre alcune nuove grandezze, la velocità angolare ω, il
momento di inerzia I e il momento angolare L.
Le equazioni per la rotazione di un corpo sono formalmente le stesse
che descrivono la sua traslazione (F=ma), con le opportune
ridefinizioni delle variabili:
F ==> M
m ==> I
a ==> α
Ripartiamo dal moto circolare uniforme
Moto circolare uniforme
ω=velocità angolare=costante, anche
il modulo della velocità è costante,
l’accelerazione è nulla?
NO. Dove è diretta? Verso il centro:
Forza centripeta
a=v2/r !S
!!
v=
=R
= R"
!t
!t
!v = v!! se angolo piccolo
!v
!!
=v
= v"
!t
!t
2
v
2
aCP = = " R
R
Costrutto geometrico
L’accelerazione e’ la differenza tra i due vettori velocita, v2-v1, diviso il
tempo dt
Geometricamente i due vettori v1 e v2 se messi con il vertice in comune
formano un triangolo isoscele, la cui base e’ quello che cerchiamo, la
differenza.
L’angolo tra i due vale Δq, esattamente lo stesso angolo che separa i due
vettori posizione CA e CB. La base di un triangolo isoscele vale:
2*ipotenusa*sin(Δθ/2) dove ipotenusa e’ il modulo di v, quindi
a=
2vsin(!! / 2) 2v!!
!!
lim
=
=v
!t" > 0
!t
2!t
!t
!S = r!!
!S v 2
a=v
=
r!t r
dove ΔS e’ l’arco di cerchio sotteso a Δθ
Energia Cinetica
Calcoliamo l’energia cinetica per la sfera
che ruota a velocità angolare costante:
1 2 1
EK = mv = mR 2! 2
2
2
I = mR 2
1 2
E K = I!
2
Introducendo il momento di inerzia I possiamo riscrivere l’energia
cinetica rispetto alla velocità angolare. Questo è importante perché
se anziché avere una sfera abbiamo un disco pieno che ruota,
possiamo riscrivere l’energia cinetica calcolando il momento
d’inerzia totale (usando un integrale). Da notare che per un disco
che ruota ogni porzione considerata ha la stessa velocità angolare
ma diversa velocità lineare.
Momento d’inerzia
Il momento d’inerzia I ha lo stesso ruolo della
massa m quando abbiamo moti rotatori:
1 2
EK = mv
2
1 2
E K = I!
2
A parità di velocità angolare ha più energia una particella che ruota
lontano dal centro del cerchio, è importante sapere dove sta la massa.
Come esempio trovare il momento di inerzia del cilindro in figura,
altezza R e base πa2.
R
I=
!r
2
dm =
R
2
R
2
2
2
! r ! dV = ! ! r " a dr = " a ! ! r
0
0
2
0
R
" r3 %
I = " a !$ '
#3&
2
I=MR2/3
0
R3
R2
R2
2
= "a !
= " a !R
=M
3
3
3
2
dr
Accelerazione angolare
Nel moto circolare uniforme la velocità
lineare è costante perché lo è quella angolare.
Se invece abbiamo che la velocità angolare
cambia allora possiamo definire
un’accelerazione tangenziale:
v = R!
!v = R!!
!v
!!
=R
!t
!t
at = R"
Equazione rotazionale
Cosa permette
un’accelerazione
tangenziale?
Sicuramente una
forza tangenziale!
F
a=
m
a
!=
R
Combinando le due espressioni possiamo scrivere
F
R F
!=
=
mR R mR
Ma il numeratore è il momento della forza rispetto al centro e il
denominatore il momento d’inerzia della nostra massa M:
M
!=
I
Ovvero M=Iα che ha la stessa struttura di F=ma
con le opportune redifinizioni!
Momento Angolare
L’equazione rotazionale si può anche
scrivere (regola mano destra):
!
!L " ! dL %
M = I! =
;$ M =
'
!t #
dt &
!
!
L = I! ; L = I!
(
)
Dove abbiamo introdotto il momento angolare L. Questa equazione ci
dice che:
1. Se abbiamo un momento di una forza M diverso da zero allora il
momento angolare L deve cambiare
2. Se L è costante (M=0) e facciamo variare I allora ω deve cambiare
Mentre il primo punto ci dà la seconda condizione di equilibrio per i
corpi rigidi, cosa vuole dire il secondo punto?
Conservazione Momento Angolare
Esempio della ballerina: una ballerina che inizia a ruotare a braccia
aperte, richiudendo le braccia riesce ad aumentare la sua velocità
angolare! Poiché diminuisce il suo momento d’inerzia I la sua velocità
angolare ω deve aumentare!
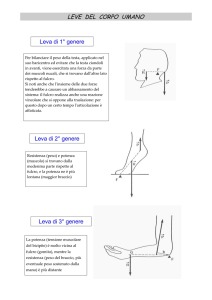
Le leve
Momento
torcente positivo
BR
Macchine semplici che compiono lavoro
moltiplicando/demoltiplicando le forze
O
BM
FR
Momento
torcente negativo
FM
Fulcro
Condizione di equilibrio della leva
BR=braccio resistente
BM=braccio motore
FR=forza resistente
FM=forza motore
BMFM=BRFR
Bm
FR =
FM = G " FM
BR
G=guadagno meccanico: proprietà geometrica della leva!
A parte la definizione di guadagno, bisogna capire se e cosa si
sta guadagnando usando una leva
!
Esempi
Guadagno!
A che distanza si deve mettere la bambina (peso minore) per
bilanciare il bambino?
30 Kg * 2.5 m = X * 25 Kg
X = 30/25 * 2.5 m = 3 m
La bambina, nonostante sia più leggera del bambino, mettendosi a
una distanza maggiore riesce a equilibrare la leva: guadagno!
Dal punto di vista del bambino invece c’è una perdita! Come mai?
Classificazione leve
BR
O
BM
FR
FM
1o tipo
BM > BR
BR > BM
G>1
G<1
Fulcro
O
FR
BM
BR
FM
2o tipo
BM > BR sempre G>1
FR
3o tipo
BR > BM sempre G<1
Fulcro
O
FM
BM
Fulcro
BR
Schema
1o tipo: la pinza
2o tipo: lo schiaccianoci
3o tipo: la valvola di sicurezza
Esempi
Pinza
Schiaccianoci
(a)
(b)
Pinzette
Nella pinza la forza applicata
ai manici viene moltiplicata a
livello della forcipe. Ma può
succedere anche l’opposto
Nello schiaccianoci c’è sempre un
guadagno. È meglio (a) o (b)?
La leva del 2o tipo è sempre favorevole!
Nelle pinzette non c’è mai un
guadagno. Non potrete mai rompere una
noce! Serve per demoltiplicare la forza.
Vedi anche valvola di sicurezza!
La leva del 3o tipo è sempre
svantaggiosa!
Articolazioni
Lezione (5) 10/10/11
Articolazioni
BM
FM
FR
O
BR
Fulcro
O
FM
BR
BM
Fulcro
FR
FR
Denti pluriradicolati
Denti monoradicolati
corona
radice
Fulcro
Bocca
Cosa è meglio fare?
Dalle figure a lato la domanda da
porsi è quale comportamento si può
considerare meno nocivo per le
articolazioni.
Per rispondere occorre conoscere le
leve e saper risolvere i problemi di
statica, qualche equazione in più
incognite.
La cosa più importante è prima di
tutto chiedersi cosa si vuole
ricavare, di solito non solo forze/
forze resistenti ma anche angoli
all’equilibrio! Definizione del
modello!!!
Il paradosso del guadagno: l’energia
Vogliamo sollevare una massa di 50 kg
per un metro.
Dalla meccanica sappiamo che il lavoro
corrisponde a L=F*s
In questo caso abbiamo 500 J
Ma se usiamo una leva con un fattore di
guadagno G=2, la forza applicata risulta
essere la metà, vuol dire che in questo
caso il lavoro fatto è anch’esso la metà?
E allora come la mettiamo con l’energia
potenziale U=mgh, dipendente solo
dall’altezza h e non dall’uso o no di una
leva? Violiamo il teorema di
conservazione dell’energia? Ricordare definizione Lavoro!!!!!!!
R2
F2
F1
Guadagno!
R1 * F1=R2 * F2
F2=R1/R2*F1
Capo
Massa 8 kg
Peso ~ 80 N
Braccio motore 2 cm (muscoli splenici)
Braccio resistente 8 cm
FRBR=FMBM
8 cm
2 cm
8kg*8cm=2cm*FM
FM=32 kg
Calcolare la reazione vincolare!
Equilibrio tronco-vertebrale
Leva del 1o tipo:
FP = Forza peso (60 kg*g) che
agisce sul baricentro del corpo,
all’altezza del ventre e anteriore
alla spina dorsale
FM = Forza Motrice, forza
esercitata dai muscoli dorsali
R = Reazione vincolare sul fulcro
(la spina dorsale) all’altezza della
settima vertebra
Equilibrio traslazionale: R= FM+FP
Equilibrio rotazionale: a*FM=b*FP
FM= b/a* FP = 2 FP = 120 kg*g=1200 Newton
R= 2 FP + FP = 3 FP = 180 kg*g=1800 Newton Piede
10 cm
Leva del 2o tipo:
FT = Forza Motrice, forza
muscolare (polpaccio) applicata dal
tendine sul calcagno
FO = Forza Resistente, forza
esercitata dalle forze peso della
gamba (tibia e fibula) sul piede
FP = reazione vincolare del suolo
sulla pianta del piede, causata dalla
forza peso del corpo che agisce sul
fulcro (punto fermo)
Piede
10 cm
Equilibri traslazionali
Verticale:
FT cos(7o) + FP = FO cos(θ)
Orizzontale:
FT sin(7o)= FO sin(θ)
Equilibrio rotazionale, rispetto al
punto centrale:
5.6 * FT cos(7o) = 10 * FP
da cui si ricava
FT=10*FP/(5.6*0.992)=1.8*FP
Sostituendo nelle precedenti
equazioni si ha:
1.8* FP *0.992+ FP= FO cos(θ)
1.8* FP *0.122= FO sin(θ)
tg(θ)=0.2196/2.7856 FP= 0.079 da cui
θ=4.5ο FO = 2.8 FP
Elasticità e legge di Hooke
Sforzo
Stiramento
F
!l
=E
A
l
! = E"
Trazione ossa Compressione ossa
E=1.8*1010 Nm-2
E=0.9*1010 Nm-2
8
! MAX = !tibia = 2.13"10 Nm
#2
Sforzo compressivo nella caduta
Una persona di 80 kg cade rigidamente su una gamba da un’altezza di
1 m. Valutare la compressione sulla gamba sapendo che una volta a
terra si ferma in dt=0.005 s
F=ma, devo calcolare la decelerazione che subisce il corpo cadendo
a=dv/dt=
v=sqrt(2gh)=4.5 m/s
a=4.5/5*10-3
F=80*4.5/5*10-3=72000 N ~100*massa
4
F 7.2 !10 N
8
"2
!= =
= 2.18!10 Nm
"4 2
A 3.3!10 m
COMP
8
#2
! MAX = !tibia = 2.13"10 Nm
Se cade su materassino caduta attenuata, dt aumenta, F diminuisce!!!
Flessione di una trave e fratture
Se immaginiamo di appoggiare una trave di peso P ai due estremi, ci
saranno due reazioni vincolari N=P/2 verso l’alto che equilibrano la
forza vincolare e i momenti rispetto al punto O.
Se analizziamo la sezione AC della trave (ombreggiata in figura), per
avere equilibrio dovro avere che sulla parte destra ci sia una forza
verso il basso pari a P/2 e un momento xP/2.
Flessione di una trave e fratture
La trave si deforma come in figura.
La parte superiore si accorcia
(compressione) e la parte inferiore
si allunga (trazione)!
Per il principio di azione e reazione sulla
sezione AC agiscono delle forze interne
che si oppongono alla deformazione,
come le frecce nere in figura, e che
tenderebbero a riportare questo piano
nella giusta posizione. Se le sollecitazioni
esterne sono maggiori delle forze interne
la trave si spezza.
Flessione di una trave e fratture
Detta l la lunghezza della
trave, la deformazione
porta un allungamento Δl,
che secondo la figura vale:
!
!
y
CC ' = l + !l = OO'+ 2ytg " l + 2y = l + y! = l + l
2
2
R
y
!l y
y
y
!l = l => = => ! = => " = E! = E
R
l R
R
R
Frattura sciatore
Lo sforzo massimo si ha in
corrispondenza della
superficie esterna (y=r)
! MAX
r
=E
R
E si ha rottura quando:
! MAX
r
= E > !tibia
R
nel caso in figura quando viene generato
un momento esterno Mf >=70kg*23cm=
1600 kg*cm ovvero quando la linea
mediana si sposta di 23 cm (sciatore).
Torsione di una trave e fratture
Un altro problema è costituito dagli effetti
delle torsioni. Quando si applicano delle
forse parallele a un piano questo può
scorrere nella direzione delle forze, come
nella figura sottostante, quando la sua base
è bloccata.
La legge di Hooke si scrive:
F
!
=G
A
h
Torsione di una trave e fratture
G, detto modulo di scorrimento, vale la meta del modulo di Young.
Per un osso lungo G=0.8-1.2 1010 Nm-2
! = G" ! G#
Torsione di una trave e fratture
Se pensiamo a una trave come formata da
fibre parallele all’asse centrale, una torsione
esterna provoca una rotazione delle fibre.
Con il calcolo integrale si dimostra che la
relazione tra la torsione esterna T e la
deformazione delle fibre ϕ vale:
G!" r
T=
2h
4
Anche qui esistono delle forze interne che si oppongono alla
deformazione e c’è la dipendenza dal raggio della trave alla quarta
potenza!
Fratture per torsione
Per ogni tipo di osso è possibile ricavare la
torsione esterna e l’angolo di torsione terminale
oltre il quale si ha la frattura.
Se prendiamo la tibia si ha rottura con un
momento torcente di soli 100 Nm (angolo 3.4
gradi). Questo tipo di frattura è tipica degli sciatori per
i quali una minima forza sulla punta dello sci
provoca una torsione che dà luogo alla frattura.
Se lo sci è lungo 1 metro, quanto deve valere la
forza sulla punta dello sci in kg per avere la
rottura della tibia? 100 Nm=10kg*g*1m!
Femore Tibia Fibula Omero Vertebra
cervicale
Vertebra
Torac. media
Vertebra
lombare
T (NM)
140
100
12
60
5
17
44
ϕ (gradi)
1.5
3.4
35.7
5.9
38
24
15
È interessante notare che se si calcola la torsione
e la deformazione di un osso cavo all’interno, la
cui massa sia uguale a quella di un osso pieno e
di uguale densità, si ha:
2
TCAVA = 2! TPIENA
dove α=r/R>1
Questo vuole dire che per le ossa cave il
punto di rottura è molto maggiore che per le
ossa piene, cioè sono più resistenti. Allo
stesso tempo, nonostante le dimensioni
maggiori di queste ossa, la massa rimane
ridotta!
Lezione (6) 13/10/11
Chiarimenti su conservazione energia
Chiarimenti su legge di Hooke
Esercizi analisi dimensionale
Esercizi sulle articolazioni
Analisi dimensionale
Si consideri il moto circolare uniforme
Si determini la formula dell’accelerazione centripeta in base
all’analisi dimensionale.
!
v
!
v
R
Il paradosso del guadagno: l’energia
Vogliamo sollevare una massa di 50 kg
R2
F2
per un metro.
Dalla meccanica sappiamo che il lavoro
F1
corrisponde a L=F*s
In questo caso abbiamo 500 J
Guadagno!
R1 * F1=R2 * F2
Ma se usiamo una leva con un fattore di
F2=R1/R2*F1
guadagno G=2, la forza applicata risulta
R2
essere la metà, vuol dire che in questo
h
h’
2α
caso il lavoro fatto è anch’esso la metà?
R1
E allora come la mettiamo con l’energia
h=2*R1*sin(α)
potenziale U=mgh, dipendente solo
h’=2*R2*sin(α)=h*R2/R1
dall’altezza h e non dall’uso o no di una
leva? Violiamo il teorema di
L1=F1*h
conservazione dell’energia? L2=F2*h’=R1/R2*F1*h*R2/R1=
Ricordare definizione Lavoro!!!!!!!
L2=F1*h
Il paradosso del guadagno: l’energia
Lo stesso problema si presenta nel torchio idraulico, quando si chiede
di valutare di quanto sale un pistone se l’altro scende di h1.
F1/S1=F2/S2
ΔV1=h1*S1=ΔV2=h2S2=ΔV
L1=F1*h1=F2*S1/S2*h1=F2/S2*ΔV
L2=F2*h2=F2*h1*S1/S2=F2*ΔV/S2
La conservazione dell’energia
Il principio di conservazione dell’energia è un principio molto forte che
permette di risolvere innumerevoli problemi, anche quando si ha di
mezzo l’attrito:
EK1+EP1=EK2+EP2+EAtt
Quando si ha attrito quasi sempre la forza di attrito viene considerata
costante lungo tutto lo spostamento.
Se io applico un lavoro su un oggetto, L=FΔS, so che sto cedendo
energia a quell’oggetto. Quindi:
1. Deve aumentare la sua energia cinetica (teorema dell’energia
cinetica)
2. Deve aumentare la sua energia potenziale
3. Potrebbe non succedere nulla (v=costante), vuol dire che tutta
l’energia è andata in attrito
La conservazione dell’energia
Anche nei casi 1 e 2 è possibile avere una certa energia persa per
attrito. Il lavoro per attrito è l’energia che ci viene a mancare
dall’applicazione del teorema di conservazione dell’energia.
Teorema dell’energia cinetica:
!v
!s = mv!v
!t
L = " dL = " mv dv = m " v dv
!L = F!s = ma!s = m
v2
L = m " v dv = m
v1
2 v2
v
2
v1
1
1
= mv 22 # mv12 = !EK
2
2
ΔL=L-ΔEK è il lavoro perso per attrito
Se poi il lavoro viene fatto contro le forze del campo, la differenza
di energia cinetica sarà negativa, cioè ho acquistato energia
potenziale, ma se non ho acquistato quella che mi aspettavo vuol
dire che c’è attrito!!!
La legge di Hooke e gli apparecchi dentali
Lo scopo degli apparecchi dentali è quello di spostare
i denti (ma non solo). Siccome i denti non sono liberi
di muoversi, sono di per sé inerti, dobbiamo agire sul
paradonto indirettamente (zona verde e rossa).
Tramite meccanismi biologici di rimodellamento
osseo, la regione rossa si ritira e quella verde si
espande. Quindi dobbiamo favorire il
rimodellamento osseo spingendo sul dente: di solito
c’ è bisogno di una forza costante che spinge sul
dente verso destra, creando una situazione di nonequilibrio, gli apparecchi fanno questo.
Questa è la legge di Hooke nella sua forma più generale:
F = !k"x = !k(x ! x0 )
Legge di Hooke
La legge di Hooke ci dice
proprio quanto vale la
forza nel caso di nonequilibrio.
All’equilibrio x=x0,
ovvero F=0
Se io modifico la
condizione di equilibrio
avrò sempre una forza di
richiamo che mi riporta il
sistema verso l’equilibrio.
F = !k"x = !k(x ! x0 )
La legge di Hooke
F = !k"x = !k(x ! x0 )
Negli apparecchi dentali si usano dei fili elastici per
“tirare” i denti. Viene creata una situazione di non
equilibrio, x>x0, dove x0 è la condizione di riposo del
filo (F=0). Perché periodicamente i fili vanno tirati? Per due motivi:
1. Perché con l’azione della forza di richiamo il dente in oggetto si
sposta più vicino alla condizione di equilibrio e la forza diminuisce.
Siccome c’è bisogno di una forza di una certa intensità per rimodellare
il tessuto, occorre “ricaricare” i fili periodicamente, altrimenti l’effetto
sarà nullo.
2. Cosi come le molle sotto sollecitazione per tempi lunghi, anche i fili
perdono la loro efficacia di “tirare”, visto che per gli apparecchi si
parla di tempi di settimane o mesi!!!
Obesità/Sovrappeso
FP = 60 kg*g
FM = 2 FP = 120 kg*g
R = 3 FP = 180 kg*g
Nel caso di obesità non solo cambia il
peso, ma anche la sua distribuzione.
Se il baricentro si sposta in avanti di
soli 4 cm abbiamo, con un incremento
del peso di 10 kg:
BR’=12 cm => aumento 4 cm, +50%
FP’=70kg*g=> aumento 10 kg, +16%
4 cm
12 cm
È interessante calcolare gli aumenti
percentuali rispetto al caso precedente:
FM= 3.0 FP’ = 210 kg*g=> +75%
R = 4.0 FP’ = 280 kg*g=> +55%
Braccio/Avambraccio
Si trovino le condizioni di
equilibrio nei due casi in figura
"M
=0
i
FM*5=FP*15+FS*35 => FM=41 kg (13 kg)
"F = 0
i
!
!
FJ+FP+FS=FM
FJ=>32 kg (10 kg)
Da notare che per una massa di 5 kg il
muscolo lavora per 41 kg, x8!!!
Se il braccio è inclinato tutte le forze che
entrano nell’equazione dei momenti
verranno moltiplicate per sin(45) e
quindi non cambia nulla!
Deltoide: FM tira verso
l’articolazione, per reazione
uguale e contraria:
FA, forza vincolare esercitata x
dall’articolazione della spalla
sul braccio
"M
i
=0
Spalla
y
θ
Rispetto all’articolazione spalla
FA ha momento zero:
24*mg=12*FM*sin(15)
FM=25.5 kg*g
Fx=24.6 kg*g
Fi = 0
Fy=(6.6-3.3) kg*g
"
Fx=FM*cos(15)
Fy+mg=FM*sin(15)
m=3.3kg
|FA|= 24.8 kg*g
θ=7.7o
Cosa cambia se aggiungo 1 kg
sulla mano?
Spalla
"M
i =0
y
1 kg
x
Rispetto all’articolazione spalla
(24*3.3+48)*kg*g=12*FM*sin(15)
FM= 40.9 kg*g (25.5 kg*g,+60%)
m=3.3kg
θ
FA: Forza vincolare esercitata dall’articolazione della spalla sul braccio
"F = 0
i
Fx=FM*cos(15)
Fy+(3.3+1)g=FM*sin(15)
Fx=39.5 kg*g
Fy=(10.2-4.3) kg*g
|FA|= 39.9 kg*g
(24.8, +60%)
θ=8.1°
(7.7, +5%)
Cosa cambia se il braccio
è raccolto?
Spalla?
y
1 kg
1 kg
x
θ
m=3.3kg
Cambia il muscolo che lavora e il braccio resistente è più piccolo!
Masticazione
Braccio Motore: 4 cm
Braccio Resistente 1 = 6+4 cm
Braccio Resistente 2 = 4+6+4 cm
FMBM=FRBR
FM=BR/BM * FR
Ammettiamo una forza di masticazione piccola di 100 N (~ 10 kg):
1o caso: FM= 10/4*10 kg=25 kg
2o caso: FM= 14/4*1 kg= 35 kg
Trovare la forza su unita di superficie per i denti anteriori (0.2 cm2) e
posteriori (1 cm2)
Flessioni
Quale forza verrà scaricata sui piedi e sulle mani?
FP+FM=P
FP*100=FM*60
Soluzione:
FP=3/8 P
FM=5/8 P
Lo sforzo è maggiore per le mani,
buona maniera per allenare i muscoli
pettorali! Per un soggetto di 60 kg, ogni mano
supporta 19 kg, cioè un terzo del
peso totale!
Anca
Studieremo in dettaglio l’articolazione dell’anca in due casi particolari:
1. Equilibrio su una sola gamba
2. Equilibrio su una sola gamba con l’ausilio di un bastone
Anca
Il primo caso rappresenta una condizione molto comune, tipica di
quando camminiamo deambulando, cioè spostando il peso da un piede
all’altro. Vedremo quali forze sono in gioco e i valori della resistenza
dell’articolazione, cioè tra la testa del femore e l’acetabolo.
In caso di indebolimento di muscoli vediamo come usando un bastone si
risolvano alcuni problemi.
Anca
Anca
Forze in gioco:
F= forza motrice esercitata dai glutei
Pg= forza peso gamba, 1/7 FP
N = reazione vincolare = FP
R = forza di resistenza che agisce
sulla testa del femore quando
all’interno dell’acetabolo, da
confrontare con P-Pg e F (reazione)
O = testa del femore, il nostro Fulcro
Da dove viene R?
Bisogna pensare alla gamba
come scorrelata rispetto al
bacino. 1) Se la forza dei muscoli F
“tira” la gamba verso il
bacino, il punto di contatto
e’ la testa del femore
sull’acetabolo. All’azione di
F corrisponde una forza di
resistenza sull’acetabolo a
cui corrisponde una reazione
R dell’acetabolo.
2) Il bacino ha un peso P a cui
dobbiamo togliere il peso
della gamba
Anca
Equilibrio Traslazionale:
Fx+Pgx+Nx+Rx=0 lungo X
Fy+Pgy+Ny+Ry=0 lungo Y
Equilibrio Rotazionale attorno a
O, quindi MR=0:
MF+MPg+MN=0
Incognite del problema: |F| e R (|R| e angolo)
Anca
θ
Fx+Pgx+Nx+Rx=0
F*cos(70)-Rx=0
Fy+Pgy+Ny+Ry=0
F*sin(70)-1/7*P+P-Ry=0
M
F+MPg+MN=0
7*F*sin(70)+3/7*P-P*11=0
Anca
θ
Dall’ultima relazione:
7*F*sin(70)+3/7*P-P*11=0
si ricava:
F=1,61*P
Dalla prima relazione F*cos(70)-Rx=0
si ricava:
Rx=0.55*P e dalla seconda relazione F*sin(70)-1/7*P+P-Ry=0
si ricava:
Ry=2.37*P
θ=atang(Ry/Rx)=76.9o
Commento-1
θ
F=1,61*P
R= 2.43*P (~ P-1/7P+F verifica!)
θ=76.9° Si ricava che:
- la forza muscolare è superiore
alla forza peso
- la forza di resistenza che agisce
sulla testa del femore è ben più
grande della forza peso!
- calcolare l’angolo di questa forza
di resistenza è utile perché di
solito le ossa crescono nella
direzione dove devono sopportare
maggiore resistenza, informazione
utile per fabbricare le protesi. Commento-2
θ
Dalla relazione F*cos(70)-Rx=0
si vede che se F=>0 allora la
componente Rx tende anch’essa
a zero, cioè R sarà quasi verticale
(θ=90). Cosa possiamo dedurre?
Se un soggetto ha i muscoli
indeboliti allora la resistenza
cambierà angolo e la testa del
femore crescerà nella direzione
del femore, allungando cosi
l’osso che causerà problemi di
scoliosi.
In questi casi l’ausilio del
bastone aiuta, vediamo come:
Bastone
Se si usa un bastone sul quale viene
scaricato 1/6 del peso corporeo le
forze F e R cambiano in valore cosi
come l’angolo θ.
Bisogna individuare la nuove forze
vincolari del suolo NP e la sua
distanza dal baricentro d
Reazioni Vincolari
Consideriamo lo schema seguente
considerando per un attimo
l’articolazione rigida, abbiamo solo
la gamba, il bastone e il suolo:
30 cm
d
NP
P
P/6
NP+P/6=P => NP=5/6*P
+ rotazione attorno ad A
NP*d=P/6*30 => d = 6 cm
Bastone
Sostituendo i nuovi valori alle
equazioni delle forze e dei momenti
otteniamo:
F*cos(70)-Rx=0
F*sin(70)-1/7*P+5/6*P-Ry=0
7*F*sin(70)+3/7*P-5/6*P*(18-7-6)=0
F=0.57*P R=1,23*P θ=81.1o
Riduzione notevole delle forze!!!
Questa condizione prevede un uso
ridotto della forza muscolare F e allo
stesso tempo non modifica l’angolo θ
della resistenza, evitando i problemi di
scoliosi.
Bastone
prima
con bastone
F=1.61 P
0.57*P R=2.43 P
1,23*P θ=76.9
81.1o
Abbiamo deambulazione con una
riduzione notevole delle forze!!!
Questa condizione prevede un uso
ridotto della forza muscolare F e allo
stesso tempo non modifica l’angolo θ
della resistenza, evitando i problemi di
scoliosi.
Esercizio 1
Un lungo recipiente cilindrico, di raggio esterno 26 cm e che vuoto
peserebbe 103 N, contiene al suo interno 20 litri di acqua. Si calcoli a
quale profondità si troverà la base del recipiente, se fosse immerso in
acqua, una volta raggiunta la condizione di equilibrio.
Fp=103N+20kg*g= 299N
Equilibrio:
Fp=SA=m’g=dV’g
Fp=d*26cm*h*g
V’
Esercizio 2
Immergendo in acqua due oggetti esteriormente identici come forma e materiale, il primo
emerge per il 33% del suo volume ed il secondo, a causa di una cavità interna vuota,
emerge per il 55%. Che percentuale del volume totale è occupata dalla cavità?
V
1) Sa=Fp
m’g=d1Vg
dV’g=d1Vg
d*0.67*Vg=d1Vg
2) Sa=Fp
m’g=d2Vg
dV’g=d2Vg
d*0.45*Vg=d2Vg
d2/d1=0.45/0.67
d2=d1*0.45/0.67<d1
m2=d2*V=d’2*V’ V-V’=cavita
(V-V’)/V=1-V’/V=1-d2/d’2
d’2=d1 1-V’/V=1-d2/d1=1-0.45/0.67=0.328
33%
Esercizio 3
Nel ramo di sinistra di un tubo ad U può scorrere liberamente uno stantuffo a tenuta, che ha
una superficie di 97 cm2, mentre il ramo di destra è del tutto aperto verso l'alto. Quando da
destra si versa nel tubo un certo fluido, la colonna nel ramo di sinistra, sotto lo stantuffo,
risulta 0.4 cm più bassa di quella nel ramo di destra. Se poi da sinistra, sopra lo stantuffo, si
versano 1.8 litri d'acqua, il dislivello tra le 2 colonne del primo fluido diventa di 2.66 cm.
Quale è pertanto la densità di questo fluido e che massa ha lo stantuffo?
• ΔP=dgΔh1=m1g/A
Non conosco m1 e d, ho bisogno di
un’altra relazione
Se aumento la massa di 1.8 kg il
dislivello sale ancora di 2.66-0.4 cm:
• m2=1.8 kg => Δh2 2.66-0.4 cm
m2g/A=dgΔh2
Δh1
Esercizio 4
Un cilindro di 130 g, cavo all'interno e con pareti di lamiera sottile,
galleggia sull'acqua, emergendone per 47% del suo volume. Se si
dovesse aprire un piccolo foro sul fondo, quanti litri d'acqua potrebbe
imbarcare il cilindro, prima di affondare definitivamente?
m=130g => Fp=0.130*9.8= 1.274 N
All’equilibrio:
Sa=m’g=dV’g=d*0.53*V*g=1.274N
La parte che sta fuori si immergera se verra
aggiunta una quantita di acqua uguale al
volume stesso che sta fuori:
La spinta di archimede e’ esattamente
UGUALE alla forza peso dell’acqua che
viene aggiunta V’=53%V
Esercizio 5
Un recipiente metallico chiuso, alto 7 m, è diviso in 2 parti da un pistone orizzontale a
tenuta, perfettamente libero di muoversi. Sul fondo poi è collegato con un lungo tubo
verticale, aperto verso l'alto. Inizialmente il pistone è completamente abbassato ed il
recipiente è completamente pieno d'aria a pressione atmosferica; poi nella parte inferiore
attraverso il tubo viene introdotta acqua fino ad un'altezza di 3.3 m. Per tenere il pistone in
equilibrio in queste condizioni, che dislivello deve esserci tra l'acqua nel tubo e quella nel
recipiente?
P1V1=P2V2
P1=1atm
V1=A*h1
V2=A*h2
P2=P1*h1/h2=1*7/3.7atm= 1.89 atm
ΔP=1.89-1 atm=0.89 atm
ΔP=dgh h=ΔP/(dg)
ΔP
7m
Δh
3.3m
Flessione di una trave e fratture
Se conosciamo lo sforzo possiamo
ricavare, per definizione, le forze agenti
sulla sezione ΔA:
!Fi = !!Ai
Possiamo quindi ricavare il momento M rispetto a O:
E 2
!M i = y!Fi = ! y!Ai = y !Ai
R
Il momento dipende dalla coordinata y, dobbiamo integrare su tutta la
superficie
Flessione di una trave e fratture
E
Mf =
R
!
A
E
y dA =
R
2
r
!
0
E !r
y ! y dy =
R 4
4
2
Il momento dipende dalla coordinata y, dobbiamo integrare su tutta la
superficie
E 2
!M i = y!Fi = ! y!Ai = y !Ai
R
" Mi = 0
Spalla
y
m=3.3kg
x
Rispetto all’articolazione spalla
24*3.3cos(45)*kg*g=12*FM*sin(15)
FM= 18.0 kg*g se pero usiamo sin(10)=>FM=26.9
θ
"F = 0
i
Adesso l’asse di riferimento e’ il braccio!
Fx=17.4 kg*g
Fx=FM*cos(15)
|FA|= 17.5 kg*g
°
θ=7.59
Fy+3.3*cos(45)*g=FM*sin(15)
Fy=2.32 kg*g
Cosa cambia se il braccio
è raccolto?
Ginocchio
Persona accovacciata: FP = metà forza peso, 40 kg
Pg = forza peso gamba, 10 kg
α=40o Trovare la forza resistente R e la
tensione del muscolo T che lavora
attraverso il legamento patellare
Equilibri Traslazionali:
T*cos(40)=R*sin(θ)
R*cos(θ)-T*sin(40)-FP+Pg=0
Equilibrio Rotazionale:
45o
T=367,1 kg; R=390,6 kg; θ=46.06