CAPITOLO I IMPATTO AMBIENTALE, ONDE
ELETTROMAGNETICHE E ANTENNE
1.1 IL CONCETTO DI IMPATTO AMBIENTALE E VIA
La
definizione
concetto
di
generale
impatto
a
cui
si
ambientale
può
è
fare
la
riferimento
seguente:
“per
per
il
impatto
ambientale si intende l’insieme di tutti gli aspetti, positivi e
negativi,
diretti
determinata
ed
opera
indiretti,
genera
temporanei
e
sull’ambiente,
permanenti
inteso
che
come
una
sistema
complesso delle risorse umane e naturali”.
Il progresso tecnologico e scientifico conduce in ogni campo ad una
migliore
qualità
comporta
una
della
serie
di
vita
dell’uomo,
ma
contemporaneamente
rischi
aggiuntivi
per
la
salute
e
per
l’ambiente nel suo complesso. Si manifesta quindi la necessità di
trovare un giusto equilibrio tra la possibilità di sfruttare tutti i
potenziali vantaggi che possono conseguire da un razionale sviluppo
tecnologico, economico e sociale, e la salvaguardia dell’ambiente.
La
valutazione
dell’impatto
ambientale
(VIA)
nasce
dalla
constatazione che il metodo scientifico non è in grado da solo di
risolvere i diversi problemi ambientali legati alle attività umane.
L’obiettivo fondamentale di tale procedura consiste nell’analizzare
e valutare la compatibilità tra un progetto e l’ambiente tenendo in
considerazione
tutti
gli
aspetti
legati
alla
realizzazione
dell’opera, compresi i pareri delle diverse componenti sociali (Enti
Statali,
regionali,
o
semplici
cittadini)
e
di
eventuali
organizzazioni private interessate.
Il principio fondamentale su cui si basa il VIA è la prevenzione di
tutte le possibili cause di impatto ambientale fin dalla fase di
progetto, in modo tale da non dover far fronte agli effetti una
volta
completata
la
realizzazione.
Al
processo
decisionale
partecipano inoltre anche varie componenti sociali oltre che gli
4
organi istituzionali preposti: ciò rappresenta un ulteriore aspetto
innovativo del VIA.
La procedura di Valutazione di impatto ambientale nasce all’inizio
degli anni settanta in USA, dove prima che in Europa, hanno dovuto
regolare lo sviluppo e gli interventi sull’ambiente.
In Europa la Direttiva CEE del 27/6/85 (85/337/CEE) stabilisce le
linee generali per la procedura di VIA ed impone il recepimento
entro il 1988 di tale direttiva da parte di tutti gli Stati membri
della Comunità sottoforma di leggi nazionali.
Il VIA si traduce in un’analisi complessa ed interdisciplinare il
cui obiettivo è pesare le scelte e renderle trasparenti in modo tale
che ai processi decisionali e alle responsabilità possano prendere
parte tutti i soggetti coinvolti. Esso ricerca, considerando tutte
le
componenti
del
problema,
non
un
compromesso,
ma
la
migliore
soluzione possibile.
Secondo le normative di legge vigenti in molti paesi del mondo una
corretta VIA deve comprendere:
-
Una
dettagliata
descrizione
dell’opera
che
si
intende
realizzare, con informazioni e dati tecnici idonei a consentire
una
adeguata
previsti
nella
analisi
fase
degli
di
effetti
costruzione
sanitari
ed
ed
ambientali
esercizio
dell’opera
stessa;
-
Una discussione degli impatti su ogni componente ambientale;
-
L’indicazione
di
ogni
effetto
negativo
che
non
può
essere
evitato;
-
Lo studio delle alternative all’opera proposta che permettono
di ottenere lo stesso risultato finale;
-
Uno studio degli effetti totali a lungo termine;
-
Ogni
utilizzo
irreversibile
o
irrecuperabile
di
risorse
naturali che l’opera potrebbe richiedere;
-
Il contributo derivante dalle azioni di consultazione delle
componenti sociali coinvolte;
5
-
Una verifica del rispetto di tutti gli atti pianificatori con
cui l’opera potrebbe interferire.
1.2 PROTEZIONE SANITARIA ED AMBIENTALE
La
protezione
sanitaria
è
la
disciplina
che
si
interessa
degli
effetti di agenti potenzialmente nocivi alla salute dell’uomo ed ha
come obiettivo l’identificazione delle concentrazioni degli agenti
nocivi che non provochino significativi danni sulla salute degli
individui
esposti.
identificati
Essa
dall’
si
basa
“International
su
alcuni
principi
Commission
for
generali
Radiological
Protection (ICRP)”, in particolare per le radiazioni ionizzanti. I
principi
della
radioprotezione
sono
tre
e,
dato
che
il
loro
carattere è estremamente generale, possono essere applicati anche a
molti
altri
settori
della
protezione
sanitaria.
La
prima
considerazione da fare comunque è che qualsiasi attività umana e
persino le condizioni naturali comportano rischi non nulli per la
salute umana: quindi il rischio zero non esiste.
Il primo principio è detto di giustificazione: ogni sorgente di
esposizione deve essere giustificata in relazione ai benefici che da
essa
si
attendono.
Il
bilancio
rischi
-
benefici
deve
essere
a
favore di un beneficio netto positivo.
L’ottimizzazione è il secondo principio e si basa sul concetto ALARA
(As Low as Reasonably Achievable), ossia il valore della dose di
esposizione
deve
raggiungibile.
essere
Esso
si
il
attua
più
basso
valore
confrontando
i
ragionevolmente
benefici
che
si
ottengono riducendo le dosi alla popolazione con l’incremento del
costo
degli
impianti.
Il
“limite
delle
dosi
individuali”,
terzo
principio, stabilisce che le dosi di esposizione di ogni individuo
non
devono
superare
determinati
limiti
fissati
da
apposite
normative. Essi peraltro devono garantire il rispetto del primo e
secondo principio.
Dall’approccio
proposto
dai
radioprotezionisti
emerge
che
il
soggetto principale della radioprotezione risulta l’uomo. In materia
6
di
protezione
ambientale
viene
proposto
di
fissare
i
limiti
di
impatto sulla base della cosiddetta “ricettività ambientale”, che
rappresenta la massima perturbazione di una variabile ambientale che
può
essere
introdotta
nell’ambiente
senza
che
l’equilibrio
del
sistema si modifichi al di là delle sue fluttuazioni ambientali.
L’inquinamento,
riferibile
a
svariate
componenti
ambientali,
costituisce un tipo frequente di impatto. “L’inquinamento ambientale
è
una
modificazione
delle
caratteristiche
fisiche,
chimiche
o
biologiche dell’aria, dell’acqua o del suolo causata dall’immissione
nell’ambiente di materia o energia, con conseguenti effetti negativi
misurabili, immediati o differiti.”
Si
parla
di
inquinamento
considerazione
sostanze
chimico
quando
organiche
ed
vengono
prese
inorganiche
in
(inquinanti
chimici); di inquinamento biologico quando microrganismi (inquinanti
biologici) vengono scaricati in dosi dannose. L’inquinamento fisico
è
caratterizzato
allo
scarico
(inquinamento
dall’immissione
in
aria
o
termico)
acqua
oppure
di
di
energia
una
alla
nell’ambiente
corrente
propagazione
di
di
dovuta
fluido
onde
caldo
sonore
(inquinamento acustico) o di onde elettromagnetiche (inquinamento
elettromagnetico).
Gli Standard di Qualità Ambientale (SQA) sono il riferimento per gli
interventi contro l’inquinamento ambientale: essi pongono i limiti
di
accettabilità
intensivo
delle
conveniente)
concentrazioni
e
dei
livelli
di
(o
di
altro
esposizione
parametro
dei
diversi
inquinanti.
1.3 ONDE ELETTROMAGNETICHE
La
luce
emessa
dal
elettromagnetiche:
sole
essa
fa
parte
raggiunge
la
della
categoria
terra
attraverso
delle
lo
onde
spazio
vuoto. Nel XVII secolo per spiegare la propagazione della luce si
postulò l’esistenza dell’etere cosmico, mezzo cosmico impalpabile ed
onnipresente. Maxwell, fisico e matematico inglese, vissuto nel XIX
7
secolo, con i suoi studi diede la definitiva spiegazione scientifica
delle onde elettromagnetiche.
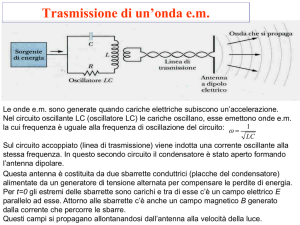
Attorno ad un conduttore percorso da corrente che varia nel tempo si
genera un campo magnetico che varia con la stessa legge, seguendo le
variazioni con un ritardo che dipende dalla distanza. La teoria di
Maxwell afferma che il campo magnetico varia, allontanandosi dal
conduttore, con la legge di un’onda che si propaga con velocità pari
a quella della luce e si manifesta con linee di forza chiuse, che
seguono le variazioni indotte dal generatore. Se si considera una
carica elettrica variabile nel tempo applicata ad una linea, per il
campo elettrico che essa produce possono essere fatte le stesse
valutazioni relative al campo magnetico, deducendo l’esistenza di
un’onda
campo
elettrico.
Come
postulato
da
Maxwell
e
verificato
sperimentalmente, un campo elettrico in variazione nel tempo origina
un campo magnetico, le cui linee di forza sono chiuse e concatenate
con le linee di forza elettriche; un campo magnetico che varia nel
tempo genera un campo elettrico, che ha linee di forza chiuse e
concatenate
fenomeno
con
che
le
linee
origina
di
onde
forza
magnetiche.
elettriche
o
Qualsiasi
magnetiche,
sia
queste
il
non
possono esistere separatamente, poiché sono vicendevolmente causa ed
effetto
del
mutuamente
e
fenomeno.
viaggiano
Esse
alla
coesistono
stessa
sempre,
velocità,
si
supportano
rappresentando
aspetti diversi di un unico fenomeno l’onda elettromagnetica.
8
due
Figura 1 Campo elettrico generato da un campo magnetico variabile.
Le
onde
elettromagnetiche
materiale,
ma
caratteristiche
solo
di
non
un
hanno
generico
dielettriche;
inoltre
bisogno
di
spazio
le
nessun
libero,
migliori
supporto
che
abbia
condizioni
di
propagazione si verificano nello spazio vuoto, dove la velocità è
c=299792458 [m/s]. La propagazione è rettilinea e valgono le leggi
dell’ottica geometrica (riflessione, rifrazione, diffrazione).
Ogni
fenomeno
elettromagnetico,
nell’ambito
macroscopico,
è
descrivibile per mezzo di un gruppo di equazioni, ”equazioni di
Maxwell”, la cui validità è data come postulato:
∇⋅D = ρ
(1.1)
∇⋅B = 0
(1.2)
∇× E = −
∂B
∂t
∇× H = J +
D
(1.3)
∂D
∂t
induzione elettrica
(1.4)
D=ε⋅E
[C/m2]
(1.5)
ε=ε0⋅εr costante dielettrica (o spostamento dielettrico)
ε0 =8.854⋅10-12 [F/m] costante dielettrica nel vuoto
εr costante dielettrica relativa
B
induzione magnetica
B=μ⋅H
9
[Wb/m2]
(1.6)
μ=μ0⋅μr permeabilità magnetica
μr permeabilità magnetica relativa
μ0=4⋅π⋅10-7 [henry/m] permeabilità magnetica nel vuoto
E
campo elettrico
[V/m]
ρ densità di carica elettrica
[C/m3]
J
densità di corrente elettrica
[A/m2]
H
campo magnetico
[A/m]
La densità di carica ρ e la densità di corrente
campo
elettromagnetico,
non
sono
tra
J,
loro
sorgenti del
completamente
indipendenti, poiché soggette alla condizione di conservazione di
carica formalizzata attraverso l’equazione di continuità:
∇ ⋅J +
La
∂ρ
= 0.
∂t
(1.7)
connessione
esplicitata
tra
(nel
elettromagnetismo
vuoto)
attraverso
e
azioni
l’espressione
meccaniche
della
forza
è
di
Lorentz:
F = ρ⋅E+ J ×B
F
(1.8)
[N/m3]
densità di forza
Le onde elettromagnetiche sono descritte da equazioni differenziali
di tipo iperbolico:
∇ 2 E − εμ
∂2 E
=0
∂t 2
(1.9)
∇ 2 B − εμ
∂2 B
=0
∂t 2
(1.10)
La
configurazione
delle
condizioni
al
contorno
cui
corrisponde
l’espressione più semplice per le soluzioni è una configurazione
piana (ad esempio ortogonale all’asse x). L’equazione diventa:
∂2 f
∂2 f
−
εμ
=0
∂x 2
∂t 2
la cui soluzione generale è:
10
(1.11)
⎛
⎞
⎜v = 1 ⎟ .
⎜
εμ ⎟⎠
⎝
ϕ (x, t ) = f1 ( x − vt ) + f 2 ( x + vt )
(1.12)
Cioè la soluzione generale è la somma di un’onda progressiva e di
una regressiva propagantesi con velocità v lungo l’asse x.
In questo caso (onda piana) tutte le componenti dei campi
indipendenti da y e z: ad ogni istante
E
e
B
E
e
B
sono
hanno lo stesso valore
in tutti i punti di ogni piano ortogonale all’asse x. Fisicamente
questa condizione non si verifica mai esattamente nella pratica:
tuttavia ci si approssima ad essa in molti casi, in particolare
quando si è interessati al campo in una porzione di spazio piccola,
molto
lontana
dalla
sorgente.
Un’onda
elettromagnetica
piana
può
essere rappresentata attraverso un sistema di riferimento su tre
piani tra loro ortogonali come mostrato in figura 2:
E
nel piano yz, ed è orientato lungo l’asse y;
E
xz ed è orientato lungo x.
direzione
di
propagazione
ed
H
H
è contenuto
è contenuto nel piano
sono inoltre ortogonali alla
dell’onda
z,
costituendo
un
sistema
tridimensionale a tre assi nello spazio. Il piano xy rappresenta il
fronte d’onda che si sposta nella direzione di z con velocità c.
Questo
tipo
parallele
al
di
onda
le
sistema
cui
di
componenti
riferimento,
rimangono
possiede
indefinitamente
per
definizione
polarizzazione lineare.
Si
può
introdurre
una
rappresentazione
matematica
mediante
una
funzione di x e t considerando il caso particolare di oscillazioni
armoniche:
z (x, t ) = z M ⋅ sin (ω ⋅ t − k ⋅ x + ϕ )
(1.13)
zM
ampiezza o valore di picco della funzione armonica
ω=2⋅π⋅ν
pulsazione della funzione armonica
ϕ
fase (valore dell’argomento della funzione seno per t=0)
κ=2⋅π/λ
numero d’onda
11
Figura 2 – Caratteristiche di propagazione di un’onda piana.
Nel caso in cui le condizioni al contorno e la configurazione delle
sorgenti
siano
tali
da
imporre
simmetria
sferica
si
ha
che
l’espressione per l’onda sferica sarà del tipo:
F (r , t ) =
1
⋅ [ f 1 (r − vt ) + f 2 (r + vt )]
r
(
v=
1
εμ
)
(1.14)
Si osserva che se si considera una piccola porzione di spazio molto
distante dal centro dell’onda sferica, il fattore 1/r può essere
considerato
praticamente
costante
e
l’onda
sferica
può
essere
approssimata con un’onda piana.
Un’onda sferica può essere rappresentata attraverso un’espressione
matematica delle coordinate spaziali e di quelle temporali:
a (r , t ) =
AM
⋅ sin[(ω ⋅ t − κ ⋅ r ) + ϕ ]
r
(1.15)
dove AM, ω, k, ϕ hanno lo stesso significato che nel caso dell’onda
piana; r indica la distanza del generico punto P dal centro O delle
superfici d’onda, nel quale può pensarsi localizzata la sorgente
dell’onda medesima.
12
Figura 3 Rappresentazione di un’onda sferica
Se
si
considera
una
superficie
chiusa
S
di
forma
costante
all’interno della quale ci sia un campo elettromagnetico non ovunque
nullo ed eventualmente della materia, l’espressione dell’energia U
posseduta
dal
campo
elettromagnetico
contenuta
in
S,
derivata
rispetto al tempo, con dτ elemento del volume τ contenuto in S è:
−
(
)
∂U
= P ∗ d S + ∫ E ∗ d S dτ
∂t ∫S
S
P = E⋅H =
(1.16)
E⋅B
(1.17)
μ
P è detto vettore di Poynting e si misura in [J/m2⋅s].
La diminuzione per unità di tempo
−
∂U
∂t
è pari alla somma della
potenza dissipata per effetto Joule nella materia contenuta in τ e
del flusso attraverso la superficie di contorno S del vettore di
Poynting
P=
E⋅B
μ
; esso rappresenta l’energia elettromagnetica che
l’onda trasporta nell’unità di tempo attraverso dS.
Quando
si
ha
a
che
fare
con
una
grandezza
periodica
a(t),
una
quantità di uso comune è il valor medio efficace A, definito dalla
seguente relazione:
13
T
A=
1
⋅ ∫ a 2 (t ) ⋅ dt
T 0
(1.18)
Per una grandezza sinusoidale, il valor quadratico medio del modulo
o valore efficace calcolato su un periodo si indica con E eff =
il
campo
elettrico,
Beff =
B0
per
il
campo
2
rappresentano l’ampiezza o valore massimo).
14
magnetico
E0
(E0
per
2
e
B0
1.3.1 SPETTRO DELLE ONDE ELETTROMAGNETICHE
L’intervallo di frequenza entro cui le onde elettromagnetiche sono
oggetto di applicazioni e di studio è molto vasto: varia tra il
migliaio di Hertz e circa 1025 Hertz. Le onde elettromagnetiche, in
base alla loro frequenza, sono originate da sorgenti diverse, hanno
caratteristiche differenti, distinte modalità di interazione con la
materia e nomi diversi.
Tabella 1
Banda di
Lunghezza d’onda
Designazione
Servizi e applicazioni tipiche
frequenza
3 - 30 Hz
30 - 300 Hz
100 - 10 Mm
10 - 1 Mm
ELF (Extremely Low
Sondaggi magnetotellurici della
Frequency)
struttura della terra
SLF (Super Low Frequency)
Rivelazione di oggetti metallici
sotterrati, distribuzione di
potenza elettrica
300 - 3000 Hz
1 - 0.1 Mm
ULF (Ulta Low Frequency)
Sondaggi ionosferici,
comunicazioni sottomarine
3 - 30 kHz
100 - 10 km
VLF (Very Low Frequency)
Segnali audio di telefonia
300 - 3000 kHz
1 - 0.1 km
MF (Medium Frequency)
Radiodiffusione a modulazione di
3 - 30 MHz
100 - 10 m
HF (High Frequency
Radiodiffusione a onde corte
30 - 300 MHz
10 -1 m
VHF (Very High Frequency)
Radiodiffusione di segnali
ampiezza (AM)
televisivi e a modulazione di
frequenza (FM),
radiocomunicazioni mobile,
controllo traffico aereo
300-3000 MHz
1 - 0.1 m
UHF (Super High Frequency)
Radiodiffusione di segnali
televisivi, sistemi radar, forni
a microonde, telefonia
cellulare.
3-30 GHz
10 - 1 cm
SHF (Ultra High Frequency)
Sistemi radar, sistemi di
telecomunicazione via satellite,
sistemi di localizzazione
geografica satellitare (GPS),
radio-navigazione aerea,
radioastronomia, telerilevamento
ambientale a microonde,
applicazioni bio-medicali
30-300 GHz
1 - 0.1 cm
EHF (Extremely High
Sistemi radar, sistemi di
Frequency)
telecomunicazione via satellite
avanzati, radioastronomia,
telerilevamento ambientale a
onde millimetriche.
15
1.4 ANTENNE
Le
antenne
sono
strutture
metalliche
su
cui
vengono
attivate
correnti che vengono utilizzate come sorgenti per la trasmissione
dell’informazione (antenne in trasmissione). Tuttavia, esse possono
anche servire come supporto per far scorrere le correnti indotte
indispensabili
per
la
ricezione
delle
informazioni
(antenne
in
ricezione).
Figura 4 Schema di un sistema di ricetrasmissione
Si consideri un campo generato da una corrente variabile che scorre
su
un’antenna
filiforme.
La
corrente
che
varia
sull’antenna
è
costituita dagli elettroni del metallo di cui è fatta la struttura:
questi cominciano a fluire lungo l’antenna stessa, alternativamente
verso il basso e verso l’alto. Come conseguenza vengono originati
effetti
variabili
con
lo
stesso
ritmo
sulle
eventuali
cariche
circostanti: tale fenomeno si rappresenta con un campo variabile che
si propaga alla velocità della luce e si attenua con la distanza. Il
campo
nel
propagarsi
mantiene
la
frequenza
delle
oscillazioni:
quindi i sistemi riceventi oscillano ad un ritmo uguale a quello dei
sistemi
inducono
trasmittenti.
correnti
che
Sulle
antenne
hanno
la
riceventi,
stessa
dell’antenna trasmittente.
16
frequenza
ad
esempio,
della
si
corrente
Figura 5 Linee di campo elettrico e magnetico prodotte da un’antenna lineare e andamento del
campo elettrico sul piano orizzontale lungo una coordinata radiale
In
figura
5
propagativo
è
generato
(rappresentazione
generatore
rappresentata
di
la
attorno
idealizzata
forza
configurazione
ad
di
un
un
conduttore
un’antenna
elettromotrice
di
fa
lineare)
scorrere
campo
filiforme
su
una
cui
un
corrente
elettrica i, variabile sinusoidalmente con la frequenza f. Le linee
del campo magnetico hanno la forma di cerchi centrati su un asse
coincidente con l’antenna (in figura 5 ne sono rappresentati alcuni
limitatamente
al
piano
“equatoriale”)
mentre
le
linee
di
campo
elettrico si avvolgono su quelle di campo magnetico in spire chiuse,
delle quali la figura mostra (in tratteggio) quelle adiacenti su un
piano meridiano (il piano del foglio).
Alle
oscillazioni
della
corrente
nel
tempo
corrispondono
oscillazioni dei campi nel tempo e nello spazio. Per quanto riguarda
lo
spazio,
ciascuno
le
dei
alternanze
quali
è
si
succedono
uguale
alla
ad
intervalli
distanza
λ
regolari,
percorsa
dalla
perturbazione elettromagnetica nel periodo di oscillazione T; cioè
c⋅T=λ, oppure essendo T=1/f: λ⋅f=c.
17
1.4.1 CAMPI ELETTROMAGNETICI A GRANDE DISTANZA DALL’ANTENNA
Se
si
utilizza
la
elettromagnetico
notazione
a
dei
vettori
componenti
complessi,
un
monocromatiche
campo
variabili
sinusoidalmente nel tempo con frequenza ν0 [Hz] e pulsazione ω0=2⋅π⋅ν0
si rappresenta:
( )
r r
E r , t = Re E (r , ω 0 ) ⋅ e − j⋅ω0 ⋅t
{
}
(1.19)
E(r,ω0)
Dove r è il vettore posizione e
è il vettore complesso
rappresentativo nel dominio delle frequenza.
Il campo elettromagnetico irradiato a grande distanza dall’antenna
(ovvero a distanze molto maggiori della dimensione dell’antenna e
della lunghezza d’onda di lavoro) in coordinate sferiche (r,θ,φ) con
sistema di versori fondamentali (r0,θ0,φ0) e notazione complessa si
rappresenta con il vettore complesso:
()
E ∞ r = E ∞ (r , θ , ϕ ) = E (r → ∞,θ , ϕ , ω 0 )
[V/m]
(1.20)
originato da un’antenna posta nel sistema di riferimento come in
figura 6.
Figura 6 Campo generato da un’antenna posta nel sistema di riferimento in coordinate sferiche
Si nota che:
-
in
coordinate
cartesiane
(x,y,z)
con
sistema
dei
fondamentali (x0,y0,z0): r=x⋅x0+y⋅y0+z⋅z0;
-
in
coordinate
sferiche
r=r·sinθ⋅cosφ⋅x0+r⋅sinθ⋅sinφ⋅y0+r⋅cosθ⋅z0.
18
versori
(1.21)
(r,θ,φ)
è
(1.22)
1.4.2 REGIONI DI CAMPO IRRADIATE DALLE ANTENNE
Le regioni di campo irradiate da un’antenna (D dimensione massima
dell’antenna tale che D>λ) si distinguono in:
1. Regione di campo vicino reattivo:
“regione del campo immediatamente circostante l’antenna in cui
prevalgono
i
campi
reattivi”.
Le
linee
di
forza
del
campo
elettrico non si richiudono in anelli attorno alle linee di
campo
magnetico,
ma
partono
dalle
cariche
di
un
segno
e
terminano su quelle di segno opposto. L’energia immagazzinata
nei campi reattivi non abbandona mai la sorgente, cioè non
viene
irradiata
Analogamente
correnti
il
che
ma
emessa
campo
e
magnetico
percorrono
i
riassorbita
è
continuamente.
localizzato
vari
elementi
intorno
alle
metallici
che
costituiscono il radiatore e le sue linee di forza si avvolgono
in anelli attorno alle correnti come per i campi magnetici
statici. I campi reattivi presentano un comportamento molto
simile a quello dei campi statici, da cui si diversificano
unicamente
per
il
fatto
che
la
loro
intensità
oscilla
nel
tempo, perciò sono chiamati anche quasi-statici. Nella regione
di campo vicino, le ampiezze del campo elettrico e magnetico
non sono legate da un rapporto costante, né possono essere
ricavate in maniera semplice le une dalle altre.
2. Regione di campo vicino (radiativo di Fresnel): r < 2⋅(D2/λ) (r
vettore posizione).
“regione
del
reattivo
e
campo
di
di
campo
un’antenna
lontano
tra
dove
i
la
regione
campi
di
di
campo
radiazione
predominano e la distribuzione angolare del campo è dipendente
dalla distanza dall’antenna. Se l’antenna ha una dimensione
massima molto più piccola della lunghezza d’onda, tale regione
può non esistere”.
3. Regione di campo lontano (radiativo di Fraunhofer): r>(2⋅D2/λ)
19
“regione del campo di un’antenna dove la distribuzione angolare
del
campo
è
essenzialmente
indipendente
dalla
distanza
dall’antenna”. In tale regione il campo elettrico e magnetico
hanno ampiezze legate tra loro che variano con 1/r. Il confine
superiore di questa regione in spazio libero è rappresentato
dal raggio della sfera all’infinito.
Tabella 2
Zona di campo
Zona di campo
Zona di campo vicino
vicino
lontano
reattivo
Limite
Zona di campo
Zona di campo
Reattivo/radiativo
Radiativo
0
λ
3⋅λ
Max(3⋅λ,2⋅D2/λ)
λ
3⋅λ
Max(3⋅λ,2⋅D2/λ)
∞
inferiore
Limite
superiore
1.4.3 CARATTERISTICHE DEL CAMPO IRRADIATO A GRANDE DISTANZA
DALL’ANTENNA
Oltre
a
proprietà
caratteristiche
di
rice-trasmittenti,
direzionalità,
le
amplificazione
antenne
possiedono
della
radiazione
elettromagnetica in alcune direzioni e riduzione della stessa in
altre.
Figura 7 Fronti d’onda del campo EM di radiazione.
20
A grande distanza dall’antenna il campo elettrico
si
propagano
come
un’onda
sferica
che
E∞
e magnetico
H∞
direzione
di
nella
propagazione può venire rappresentata localmente come un’onda piana
e uniforme (trasversa elettromagnetica: TEM rispetto alla direzione
di
propagazione
radiale
r0).
Le
superfici
equifase
del
campo
irradiato sono sferiche con centro nell’origine (in cui si individua
il centro di fase dell’antenna) e la direzione di propagazione è
radiale secondo r0.
Il campo elettrico
E∞
e magnetico
H∞
sono tra loro perpendicolari ad
ogni istante alla direzione radiale r0 ed hanno componenti (Eθ,Eφ) e
(Hθ,Hφ).
I moduli di
E∞
e
H∞
decrescono con la distanza come 1/r e sono in
rapporto costante pari all’impedenza caratteristica del mezzo η =
μ
ε
(η=377Ω).
Il campo
minimi
e
E∞
è in fase con
zeri
nello
stesso
H∞,
ossia i campi presentano massimi,
istante
e
l’onda
TEM
è
polarizzata
ellitticamente sul piano traverso, perpendicolare a r0.
1.4.3.1 DENSITÁ DI POTENZA
In virtù delle proprietà di onda piana localmente uniforme segue che
dall’espressione del vettore di Poynting: P ∞ (r , θ , ϕ ) = P(r → ∞, θ , ϕ ) nel
dominio della frequenza a grande distanza dall’antenna:
∗
1
P ∞ (r ,θ , ϕ ) = ⋅ E ∞ (r ,θ , ϕ ) × H ∞ (r , θ , ϕ ) [W/m2] dove:
2
E∞(r,θ,ϕ)e H∗∞(r,θ,ϕ)
coincidono
con
il
campo
(1.23)
elettrico
[V/m]
e
magnetico [A/m] irradiati dall’antenna a grande distanza;
⎢P∞(r,θ,ϕ)⎢ è la densità di potenza [Wb/m2] irradiata dall’antenna
attraverso una superficie ortogonale alla direzione di propagazione
r0;
21
Re[P∞(r,θ,ϕ)] è il valore medio nel periodo della densità di potenza
irradiata (ipotesi di campi monocromatici).
Si rileva che:
-
il vettore di Poynting
P∞
risulta diretto radialmente, cioè
ortogonale alle superfici equifase del campo;
-
il
vettore
di
Poynting
P∞
è
puramente
reale
in
mezzi
non
dissipativi.
1.4.3.2 POTENZA TRASMESSA (IRRADIATA)
P∞(r,θ,ϕ)=⎢P∞(r,θ,ϕ)⎢,
Se
il
flusso
del
vettore
di
Poynting
attraverso una sfera di raggio r, con centro nell’origine e normale
n0=r0 all’elemento di superficie dS, rappresenta la potenza trasmessa
(o irradiata ) dall’antenna data da:
WT ≡ ∫ P (r , θ , ϕ ) ⋅ n 0 ⋅ dS = ∫ P (r , θ , ϕ ) ⋅ dS
S
∞
S
[W]
∞
(1.24)
dove WT è la potenza trasmessa (irradiata) dall’antenna.
1.4.3.3 INTENSITÁ DI RADIAZIONE
Se
P∞(r,θ,ϕ)=⎢P∞(r,θ,ϕ)⎢,si
definisce a grande distanza dall’antenna:
U (θ , ϕ ) ≡ r 2 ⋅ P∞ (r ,θ , ϕ )
[W/sr]
(1.25)
dove: U(θ,φ) è l’intensità di radiazione irradiata dall’antenna (o
diagramma di radiazione in potenza). U(θ,φ) rappresenta la potenza
per unità di angolo solido [W/sr] trasmessa (irradiata) dall’antenna
nell’intorno della direzione (θ,φ).
L’espressione per la potenza trasmessa diviene:
WT = ∫ P
S
∞
(r ,θ , ϕ ) ⋅ dS
U (θ , ϕ )
=∫
⋅ dS = ∫ U (θ , ϕ ) ⋅ dΩ =
S
r2
4π
2π π
∫ ∫ U (θ , ϕ ) ⋅ sin θ ⋅ dθ ⋅ dϕ
[W]
0 0
(1.26)
Si nota che:
-
L’intensità di radiazione non dipende dalla distanza r poiché a
grande distanza la densità di potenza irradiata varia in modo
22
inversamente proporzionale al quadrato della distanza. Si noti
che ciò non è più vero in zona di campo reattivo;
-
U(θ,φ) caratterizza le proprietà direzionali dell’antenna.
1.4.4 CARATTERISTICHE DIREZIONALI DI UN’ ANTENNA
Un’antenna
è
isotropica
un’“antenna
ipotetica
avente
uguale
radiazione in tutte le direzioni.”
Un’antenna
puntiforme
è
un’antenna
isotropica
non
fisicamente
realizzabile la cui intensità di radiazione Uiso non dipende dalla
direzione e che ha la proprietà di distribuire uniformemente in ogni
direzione tutta la potenza irradiata.
U (θ , ϕ ) = U iso = r 2 ⋅ P∞iso
2π π
WT = ∫ U iso ⋅ dΩ =
∫ ∫ sin θ ⋅ dθ ⋅ dϕ = P
∞ iso
4π
Un’antenna
(1.27)
⋅ r 2 ⋅ 4 ⋅π
(1.28)
0 0
è
direzionale
un’“antenna
avente
la
proprietà
di
irradiare e ricevere onde elettromagnetiche in modo più efficace in
alcune direzioni piuttosto che in altre”.
Un’antenna omni-direzionale è un’“antenna avente proprietà radiative
non
direzionali
sul
piano
azimutale
(θ=90°,
φ
variabile)
e
direzionali su piani di elevazione (φ = costante, θ variabile).
Esempio: dipolo.
1.4.5 SOLIDO DI RADIAZIONE
Il
solido
di
“rappresentazione
radiazione
radiazione
grafica
(intensità
(“radiation
pattern”)
tridimensionale
di
radiazione,
delle
è
proprietà
ampiezza,
fase,
una
di
o
polarizzazione del campo) dell’antenna in funzione delle coordinate
direzionali” [IEEE Std 145-73].
Si possono ottenere:
Un
solido
di
radiazione
in
campo
|E∞(r,θ,φ)| per r = costante
23
ossia
una
rappresentazione
di
Un solido di radiazione in potenza ovvero una rappresentazione di
U(θ,φ) oppure |E∞(r,θ,φ)|2 per r costante.
La
rappresentazione
del
solido
di
radiazione
può
essere
di
due
tipologie: in figura 8 sono mostrate la rappresentazione polare a
sinistra e a destra la rappresentazione assonometrica.
Figura 8 Rappresentazione polare del solido di radiazione e rappresentazione assonometrica
Il lobo di radiazione (“radiation lobe”) è la porzione del solido di
radiazione delimitata da regioni a relativa bassa radiazione. Si
possono incontrare:
-
Lobo principale (“major lobe”): lobo di radiazione contenente
la direzione del massimo di radiazione.
-
Lobo secondario (“minor lobe”): ogni lobo di radiazione eccetto
il principale.
-
Lobo laterale (“side lobe”): ogni lobo in direzione diversa da
quella considerata (generalmente del massimo).
-
Lobo posteriore (“back lobe”): lobo secondario in direzione
opposta al principale.
1.4.6 DIAGRAMMA DI RADIAZIONE
Il
diagramma
di
(“antenna
radiazione
pattern”)
è
una
rappresentazione bidimensionale del solido di radiazione mediante
sezioni a φ = costante o θ = costante, che serve per caratterizzare
24
l’antenna.
In
esso
radiazione
relativa
trasmittente.
ricezione
Nel
vengono
che
caso
rappresenta
riportate
l’antenna
di
la
nelle
emette,
antenna
risposta
diverse
nel
caso
ricevente,
relativa
direzioni
il
di
la
antenna
diagramma
dell’antenna
di
alla
radiazione elettromagnetica incidente dalle diverse direzioni. Se la
radiazione trasmessa e quella ricevuta sono polarizzate ugualmente,
il
diagramma
di
radiazione
e
quello
di
ricezione
di
un’antenna
coincidono. I diagrammi di radiazione e di ricezione possono essere
forniti in formati diversi, ossia in termini di
-
attenuazione;
-
potenza
effettiva
irradiata
(ERP
o
Effective
Radiative
Power), espressa in relazione a riferimenti vari (dBk, dBm);
-
intensità di campo relativa.
Essi possono essere rappresentati o in scala lineare o in scala
logaritmica. Le forma più diffuse rappresentano in scala lineare
l’intensità relativa di campo e in scala logaritmica l’attenuazione.
Esistono
diagrammi
di
radiazione
in
coordinate
cartesiane,
che
trovano utilizzo nel caso particolare in cui sia necessario o si
desideri descrivere nel dettaglio anche i cosiddetti lobi secondari
(figura 9), tuttavia in genere sono forniti diagrammi di radiazione
in forma di grafici polari, un esempio in figura 10.
Figura 9 Rappresentazione cartesiana del diagramma di radiazione
25
La Larghezza del fascio a metà potenza è l’ampiezza angolare del
lobo principale a metà potenza (a -3 dB) (Half Power Beam Width,
HPBW).
Figura 10 Rappresentazione polare del diagramma di radiazione
1.4.7 DIRETTIVITÀ O GUADAGNO DIRETTIVO
La direttività o guadagno direttivo (“Directive gain”) è definita
dalla seguente formula:
D(θ , ϕ ) =
P∞ (r ,θ , ϕ ) U (θ , ϕ ) P∞ (r ,θ , ϕ ) U (θ , ϕ )
=
=
=
P∞iso
U iso
WT / 4π ⋅ r 2 WT / 4π
[adimensionale] (1.29)
Si nota che:
-
La
direttività
è
una
figura
di
merito
per
le
proprietà
direttive dell’antenna rispetto al riferimento di un’antenna
isotropica
che
irradi
la
stessa
potenza
WT;
a
volte,
il
riferimento può essere un’antenna nota non-isotropica (esempio:
antenna a tromba).
-
La direttività di un’antenna isotropica è unitaria Diso(θ,φ)=1.
-
Si usa, in genere, il valore in dB della direttività:
Ddb (θ , ϕ ) = 10 ⋅ Log 10 [D(θ , ϕ )]
(1.30)
26
1.4.8 GUADAGNO DI UN’ANTENNA
Il guadagno (“power gain”) si definisce similmente alla direttività,
ma riferendosi alla potenza alla porta di ingresso dell’antenna WIN
(invece che alla potenza irradiata). Il guadagno evidenzia come la
maggiore potenza che si riesce ad irradiare in una certa direzione,
si ottenga riducendo la potenza in tutte le altre direzioni.
Viene definito secondo lo standard IEEE come “Rapporto, moltiplicato
per 4π, dell’intensità di radiazione rispetto alla potenza netta
accettata dall’antenna da un trasmettitore ad essa connesso”.
G (θ , ϕ ) ≡
P∞ (r , θ , ϕ )
U (θ , ϕ )
=
= η r ⋅ D(θ , ϕ ) [adimensionale]
2
WIN / 4 ⋅ π
WIN / 4 ⋅ π ⋅ r
(1.31)
dove:
WIN: potenza alla porta di ingresso dell’antenna tale che WIN–WT è
pari alla potenza WL perduta per dissipazione (“losses”).
ηr: efficienza di radiazione dell’antenna, che tiene conto delle
perdite dovute alla dissipazione per conduzione e dielettricità,
ed è definita da:
ηr ≡
WT
WIN
Essendo WIN≥WT si ha che 0≤ηT≤1 con:
G(θ,φ)≤D(θ,φ)
-
ηr=1 per antenne senza perdite;
-
ηr=0 per antenne con perdite “infinite”.
1.4.9 CLASSIFICAZIONE DELLE ANTENNE
Le antenne possono essere classificate in base alla loro struttura e
configurazione in:
•
Antenne lineari: antenne la cui struttura è di tipo filiforme,
in
generale
di
spessore
finito
(sottile)
e
a
geometria
variabile (rettilinea e non).
Esempi:
dipoli,
spire,
monopoli,
antenne
Beverage,
antenna
rombica, antenna a elica, antenna biconica, antenna a farfalla.
27
•
Antenne
apertura: antenne la cui struttura presenta una
ad
porzione
di
superficie
piana
(bocca)
attraverso
la
quale
avviene l’irradiazione di onde elettromagnetiche (tale bocca
può essere rappresentata anche da una superficie dielettrica,
come nelle antenne a lente).
Esempi:
antenna
a
guida
troncata,
antenna
a
tromba,
microstriscia.
•
Antenne a riflettore: antenne che presentano un illuminatore
(antenne ad apertura) che irradia verso uno o più riflettori
metallici,
avente
caratteristiche
di
irradiazione
elettromagnetiche altamente direttive.
Esempi: antenna a riflettore parabolico, antenna a riflettore
angolare, antenna a riflettore fuori-asse, antenna a doppio
riflettore di tipo Cassegrain.
•
Allineamenti di antenne: configurazioni mono o bi-dimensionali
di antenne (dette primarie, di tipo lineare o ad apertura)
alimentate
avente
con
opportuna
caratteristiche
distribuzione
di
di
irradiazione
ampiezza
e
fase,
elettromagnetiche
altamente direttive e facilmente riconfigurabili.
Esempi: allineamento mono e bi-dimensionali a dipoli risonanti,
allineamento
mono
allineamento
a
e
bidimensionali
microstriscia,
in
guida
allineamento
fessurata,
di
tipo
logperiodico, allineamento di tipo Yagi - Uda, allineamento
mono e bi-dimensionale con antenne primarie “attive”.
28