TRASFORMAZIONI TERMODINAMICHE
Le trasformazioni termodinamiche sono le modificazioni
della materia di natura chimica o fisica, reversibili o
irreversibili, prodotte da una variazione di temperatura.
Le trasformazioni termodinamiche occupano un ruolo
centrale nella scienza dei materiali.
La quasi totalità dei metalli e delle leghe è prodotta per
fusione e solidificazione.
Le proprietà dei metalli vengono modificate attraverso dei
trattamenti termici.
La produzione di leghe magnetiche si riduce
sostanzialmente ad una successione di trattamenti termici
spesso alternati a trattamenti meccanici, e così via.
94
Le trasformazioni termodinamiche vengono presentate sotto
forma di diagrammi termodinamici come:
- diagrammi di fase all’equilibrio
- diagrammi delle trasformazioni di fase
I diagrammi di fase all’equilibrio, o diagrammi di stato,
danno la possibilità di individuare i campi di concentrazione e
temperatura (supponendo la pressione costante) nei quali è
stabile una certa fase.
Nel caso di sistemi metallici binari, nella grande maggioranza
dei casi, allo stato liquido si verifica una completa miscibilità
dei componenti della lega e, pertanto, si ha solidificazione
partendo da una miscela fusa omogenea.
Tali diagrammi, costruiti sulla base di risultati sperimentali,
indicano per ogni composizione della lega, corrispondente a
determinate concentrazioni dei suoi costituenti:
- la temperatura di completa fusione della lega (o
temperatura di inizio solidificazione)
- l’ampiezza dell’intervallo di solidificazione, cioè la
temperatura di fine solidificazione (o temperatura di inizio
fusione)
95
- i vari campi nei quali si può suddividere il diagramma, ad
ognuno dei quali corrisponde una particolare struttura della
lega, conseguente ad un particolare modo di raggrupparsi dei
suoi costituenti.
96
Definizioni:
Viene chiamato sistema il complesso costituito dal materiale
in esame e dall’ambiente con il quale esso interagisce.
Fase di un sistema è una parte di esso nella quale la
composizione (natura e concentrazione delle specie atomiche
presenti) e la struttura (distribuzione spaziale delle specie
atomiche) sono costanti o variano con continuità.
Una fase risulta separata dal sistema da superfici definite,
lungo le quali la composizione e la struttura presentano
variazioni discontinue.
I tre stati della materia - gas, liquido e solido - costituiscono
gli esempi più semplici di fasi nel caso di sostanze pure.
Tuttavia, una singola fase non necessariamente corrisponde
ad uno stato, come mostrato in tabella dal polimorfismo del
ferro.
Tabella 1 - Fasi del ferro allo stato solido
Temperatura (°C) Struttura Cristallina Fase
*
-273÷912
912÷1394
1394÷1538*
CCC
CFC
CCC
Temperatura di fusione
97
α
γ
δ
Sebbene l’acqua e l’alcol siano miscibili in tutte le
proporzioni, come lo sono il rame ed il nichel (soluzione
solida), una miscela di acqua ed olio forma un’emulsione,
cioè una dispersione di piccolissime goccioline di olio in
acqua corrispondente all’esistenza di due fasi nello stesso
liquido.
Un fenomeno analogo avviene nello stato solido, quando ad
esempio, viene superata nel ferro la solubilità del carbonio, o
di altre impurezze in esso contenute, ad una determinata
temperatura. Si dice allora che una fase precipita in un’altra.
Anche i polimeri rinforzati con fibra di vetro o polvere di
silice od altri componenti ad essi aggiunti forniscono un
esempio di materiali con diverse fasi.
98
Il concetto di equilibrio:
Un sistema è in equilibrio chimico-fisico quando i suoi
costituenti, dall’istante in cui il sistema viene preso in esame,
non cambiano né di stato fisico né di stato chimico, e le
proporzioni che collegano questi costituenti al sistema stesso
rimangono invariate.
Si intende un equilibrio stabile quando è valido il principio di
Le Chatelier:
“Se in un sistema in equilibrio viene variato il valore di uno
dei parametri che regolano l’equilibrio, il sistema reagisce
variando gli altri parametri in modo tale da mantenere
inalterato il preesistente stato di equilibrio”.
L’equilibrio dei sistemi omogenei, nei quali tutti i componenti
si trovano in uno stesso stato fisico, viene regolato
principalmente dalla legge di azione di massa.
99
Lo studio dell’equilibrio di sistemi eterogenei, invece, si basa
fondamentalmente sulla regola delle fasi di Gibbs:
nf x
(1)
Dove:
ν = varianza
f = numero fasi simultaneamente presenti
n = numero dei componenti del sistema
x = numero delle variabili fisiche (pressione e temperatura)
Se, come spesso accade, la pressione viene mantenuta
costante la regola delle fasi può essere scritta:
n f 1
(2)
La varianza ν di un sistema è il numero delle variabili
(pressione, temperatura, o concentrazione) che possono
variare in un certo campo indipendentemente dalle altre senza
che cambi il numero delle fasi presenti nel sistema.
Il numero di gradi di libertà del sistema è un altro modo di
esprimere la varianza.
Il numero di componenti del sistema n è il numero minimo
di costituenti chimici distinti la cui concentrazione deve
essere nota per definire la composizione di ciascuna fase.
100
DIAGRAMMI DI FASE ALL’EQUILIBRIO
Un diagramma di fase all’equilibrio, o più semplicemente un
diagramma di equilibrio, è un diagramma che descrive lo
stato al quale il sistema tende in funzione dei valori delle
variabili considerate.
Il diagramma di equilibrio non dà alcuna informazione sul
tempo necessario per raggiungere l’equilibrio.
Quando il sistema ha un solo componente e le variabili sono,
ad esempio, pressione e temperatura, il diagramma di
equilibrio viene rappresentato in due dimensioni. Con due
componenti il diagramma sarà rappresentato in tre
dimensioni.
Allo
scopo
di
mantenere
una
rappresentazione
bidimensionale, che è molto più pratica, la pressione può
essere assunta come parametro costante nel diagramma
rappresentato.
La temperatura viene allora riportata sull’asse delle ordinate
ed il rapporto fra le quantità dei due componenti sull’asse
delle ascisse.
Questo diagramma, chiamato diagramma binario (a due
componenti), ha una particolare importanza.
101
102
I sistemi a più componenti vengono spesso descritti con una
serie di diagrammi binari nei quali le variabili non
rappresentate vengono assunte come parametri costanti nel
diagramma.
Il diagramma binario fornisce le seguenti informazioni:
il numero delle fasi presenti
la composizione di ciascuna fase
la frazione di ciascun componente presente in ciascuna fase
103
Curve di raffreddamento
La curva di raffreddamento di un sistema descrive
l’andamento della temperatura in funzione del tempo durante
un processo di raffreddamento, dallo stato liquido allo stato
solido, sufficientemente lento da poter considerare ad ogni
istante la temperatura costante in ogni punto del sistema.
Queste curve sono usate per costruire i diagrammi di
equilibrio.
Su di esse si rilevano le temperature di trasformazione, che
sono rappresentate da punti singolari (generalmente cuspidi)
in corrispondenza di improvvise variazioni di temperatura.
104
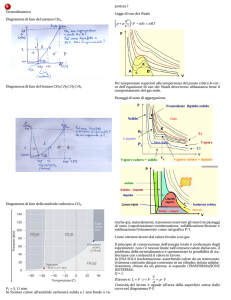
Nei sistemi ad un solo componente (monometallici) la curva
di raffreddamento può assumere tre aspetti diversi secondo
che si abbia (fig.1):
(a) solo un cambiamento di stato fisico
(b) anche una trasformazione allotropica
(c) sottoraffreddamento.
Nel caso classico che si manifesti solo un cambiamento di
stato fisico alla temperatura di equilibrio TS0 , la temperatura
dapprima decresce esponenzialmente nel tratto 1-2 (fig. 1(a))
con pendenza definita dal calore specifico del metallo fuso e
dalla sua massa.
Successivamente, nel tratto 2-3 la temperatura rimane
costante e pari alla temperatura di equilibrio TS0 del
cambiamento di stato liquido-solido per tutto il tempo
necessario al completamento della trasformazione stessa.
Infine, nel tratto 3-4 la temperatura diminuisce di nuovo
esponenzialmente con pendenza definita dal calore specifico
del metallo solido.
105
Con la regola delle fasi (2) (p = costante), si ha:
tratto 1-2: n = 1, f = 1, ν = 1, sist. monovariante (T varia)
tratto 2-3: n = 1, f = 2, ν = 0, sist. invariante (T = cost.)
tratto 3-4: n = 1, f = 1, ν = 1, sist. monovariante (T varia)
Una varianza nulla (ν = 0) significa che la trasformazione
avviene a temperatura costante, perché il calore che si
sottrae dall’esterno uguaglia quello emesso dalla massa che
diventa solida (calore latente di solidificazione).
Nel caso in cui, dopo il cambiamento di stato fisico, si
manifesti una trasformazione allotropica (fig.1(b)) alla
temperatura Tta0 , per quest’ultima tutto procede in perfetta
analogia al cambiamento di stato fisico.
La trasformazione allotropica non è altro che una
modificazione del reticolo cristallino: durante tale
trasformazione si hanno due fasi che si differenziano per il
reticolo cristallino, quindi il sistema risulta invariante.
Lo studio dell’analisi termica dei sistemi a due componenti
lasciati raffreddare lentamente dallo stato fuso, permette di
stabilire l’andamento dei diagrammi di stato o di equilibrio di
tali sistemi binari.
106
In questo caso, tuttavia, non si può più fare riferimento ad un
unico schema di curva di raffreddamento, ma è necessario
distinguere vari casi secondo che i due componenti
cristallizzino separatamente oppure siano parzialmente o
totalmente miscibili allo stato solido oltre che allo stato
liquido.
107
Diagramma di fase binario elementare
Il diagramma di fase binario elementare è il diagramma di
equilibrio corrispondente al caso in cui i due componenti A e
B siano miscibili in tutte le proporzioni sia allo stato solido
che allo stato liquido.
La forma di questo diagramma può essere dedotta dalle curve
di raffreddamento di A, di B e delle miscele A+B, mostrate in
fig.2, dove T rappresenta la temperatura e t il tempo.
Ciascuno dei diagrammi della fig.2 può essere considerato
come una sezione trasversale del diagramma tridimensionale
mostrato in fig.3.
La regola delle fasi consente la seguente interpretazione della
fig.2.
Nel caso della fig.2(a), esiste un solo componente (n = 1) ed è
del tutto analogo al caso di fig.1a.
Nell’istante che precede il tempo t1' , una sola fase, quella
liquida, è presente (f = 1), e perciò esiste un solo grado di
libertà (ν = 1).
Di conseguenza, la temperatura può variare entro certi limiti
senza modificare il numero delle fasi presenti.
108
Nell’intervallo t1' t t1" risulta f = 2 da cui si deduce ν= 0,
ciò significa che, per tutto il tempo che le fasi liquida e solida
coesistono, la temperatura si mantiene costante.
Durante questo intervallo di tempo, il sistema cede il calore
latente di fusione di A.
Non appena t t 1" , il sistema risulta completamente solido
(f = 1) e la temperatura può continuare a diminuire. Il caso
della fig.2(e) è del tutto simile.
109
Il caso delle Figure 2(b), (c) e (d) si differenzia da quello
delle Figure 2(a) ed (e) principalmente quando t 1' t t 1" .
In questi intervalli di tempo risulta f = 2, ma, dal momento
che anche n = 2, dalla regola delle fasi (2) si ottiene ν = 1.
Perciò, la temperatura del sistema continua a diminuire
durante l’intervallo di solidificazione.
110
Immaginando di realizzare una curva di raffreddamento per
ogni valore di concentrazione A-B, si può pensare di
realizzare il diagramma tridimensionale di fig. 3 nel quale, il
terzo asse rappresenta la frazione molare (o in peso) del
componente B.
111
Il diagramma di fase binario vero e proprio viene ottenuto
diagrammando i punti Ti e Ti" per tutte le curve di
raffreddamento in funzione della composizione del sistema
espressa in termini di frazione in peso X di B (fig.4).
112
I luoghi geometrici dei punti Ti e Ti" sono rispettivamente
chiamati curva di liquidus e curva di solidus.
La fig.4 corrisponde alla rappresentazione che si otterrebbe
per il diagramma tridimensionale di fig.3 osservandolo da un
punto situato all’infinito sull’asse t.
Per un sistema di composizione X0, il diagramma binario
fornisce le seguenti informazioni:
alla temperatura Ta, il sistema è completamente liquido
alla temperatura Tb, nella fase liquida di composizione X0
appare una fase solida di composizione Xsi, più ricca in B
rispetto alla fase liquida
alla temperatura Tc, una fase liquida di composizione Xl ed
una fase solida di composizione Xs coesistono
alla temperatura Td, le ultime tracce della fase liquida di
composizione Xlf solidificano nella fase solida di
composizione X0
alla temperatura Te, il sistema è completamente solido
113
Pertanto, la curva di liquidus fornisce la correlazione fra
composizione e temperatura della fase liquida in equilibrio
con la fase solida.
Analogamente, la curva di solidus fornisce la correlazione fra
composizione e temperatura della fase solida in equilibrio
con la fase liquida.
114
La regola della leva
Il diagramma di fase binario consente di calcolare la quantità
di materia presente in ciascuna fase.
Siano M la massa totale del sistema, ML la massa della fase
liquida e MS la massa della fase solida.
Per un sistema di composizione X0, ad una qualsiasi
temperatura Ti compresa nell’intervallo di solidificazione, si
può scrivere il seguente bilancio di massa rispetto a B:
X 0 M X L M L X SM S
Essendo
M M L MS MS M M L
(5)
(6)
si ottiene: X 0 M M L X L M M L X S
da cui:
ML
XS X 0
M
XS X L
(9)
La massa di fase liquida è proporzionale al segmento XS-X0.
115
Con un procedimento analogo si ottiene:
X0 XL
MS
M
XS X L
La massa di fase solida è proporzionale al segmento X0-XL
116
Diagramma binario con eutettico
Accade frequentemente che due componenti miscibili allo
stato liquido abbiano una solubilità limitata allo stato solido.
Il caso più comune è quello di una trasformazione eutettica
(fig.5).
Una trasformazione eutettica è una trasformazione isoterma
durante la quale una fase liquida viene simultaneamente
trasformata in due differenti fasi solide:
L αβ
Sia α la fase solida del componente A contenente una quantità
di B inferiore alla solubilità limite di B in A (soluzione solida
di B in A).
Analogamente, sia β la fase solida del componente B
contenente una certa quantità A in soluzione solida.
117
Nel diagramma si possono individuare:
due archi di curva del liquido che si intersecano nel punto
eutettico, che definisce la temperatura eutettica Te e la
composizione eutettica Xe
due archi di curva del solido situati rispettivamente fra le
temperature di fusione di A puro e B puro, e la temperatura
eutettica Te
due archi di curva di solubilità (solvus).
Solvus è il nome dato alla correlazione fra composizione e
temperatura di una fase solida in equilibrio con un’altra fase
solida.
Quando una miscela di composizione X0 viene raffreddata a
partire da una temperatura Ta, si ottiene la seguente
successione di stadi di equilibrio:
alla temperatura Tb, appare la fase α di composizione Xα1
alla temperatura Tc, la fase α di composizione Xα coesiste
con la fase liquida di composizione Xl: il sistema ha un
grado di libertà
alla temperatura Te, appare la fase β: la presenza simultanea
di tre fasi (liquido, α e β) rende il sistema invariante in base
alla regola delle fasi (2). La solidificazione della fase
118
liquida residua avviene a temperatura costante e, durante
questa trasformazione, si depositano contemporaneamente
cristalli di α e di β, che solidificano in un’intima miscela
eterogenea, chiamata miscela eutettica, di piccole particelle
di ciascuna delle due fasi, di composizione Xαe e Xβe
rispettivamente
alla temperatura Tf, esistono solo le fasi α e β, di
composizione Xα2 e Xβ2 rispettivamente
per ulteriori diminuzioni di temperatura, Xα diminuisce,
mentre Xβ cresce, poiché le solubilità di B in α e di A in β
diminuiscono.
119
120
Nel diagramma in fig.5 si possono osservare, alla temperatura
Tf, le frazioni in massa di B in β in equilibrio con α e di B in
α in equilibrio con β, individuate dalle rispettive curve di
solubilità (solvus).
La struttura del materiale nello stato solido dipende dalla
composizione X0.
Se X0 < Xe, la prima fase solida ad apparire durante il
raffreddamento è la fase α.
Quando la temperatura eutettica Te viene raggiunta,
l’accrescimento dei grani cristallini di α risulta interrotto e,
per T < Te, tali grani vengono incapsulati nella miscela
eutettica (fig.6(a)).
Se X0 > Xe, avviene lo stesso fenomeno per la fase β
(fig.6(c)).
Infine, se X0 = Xe, la fase solida è costituita solamente dalla
miscela eutettica (fig.6(b)), che solidifica a temperatura
costante come una sostanza pura (costituita da un solo
componente).
121
122
Nella pratica, i diagrammi di stato a due componenti possono
avere altre trasformazione caratterizzate dalla presenza
contemporanea di tre fasi.
Le più comuni sono:
Trasformazione Peritettica: L
Trasformazione Eutettoidica:
Anche queste trasformazioni sono zerovarianti.
123
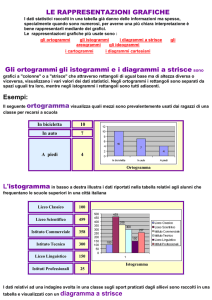
Esempio del sistema ferro-carbonio (o Fe-Fe3C)
Nel sistema Fe-C, il carbonio è presente all’equilibrio sotto
forma di grafite.
Tuttavia, in condizioni normali di raffreddamento (p.es.
raffreddamento naturale all’aria), non si forma grafite ma
carburo di ferro, Fe3C un composto metastabile la cui
cinetica di decomposizione è molto lenta (impiega parecchi
milioni di anni per trasformarsi in ferro e grafite).
Per questo motivo ci si può riferire al diagramma di equilibrio
Fe-Fe3C (fig.8).
Oltre alla fase liquida L, il diagramma Fe-Fe3C coinvolge le
tre fasi del ferro: α, γ e δ, ed il carburo di ferro (cementite).
A 1495°C e per un ristretto campo di concentrazioni Xc,
avviene una trasformazione peritettica corrispondente ad una
delle seguenti reazioni:
L + Feδ → Feγ + Feδ
per Xc < 0.2 %
L + Feδ → L + Feδ
per Xc > 0.2 %
L + Feδ → Feγ
per Xc = 0.2 %
124
A 1148°C e per Xc > 0.2·%, avviene una trasformazione
eutettica, con composizione della miscela eutettica Xc =
4.3·10-2.
A 727°C, avviene una trasformazione eutettoide che
coinvolge una delle tre seguenti trasformazioni:
Feα + Feγ → Feα + Fe3C
per Xc < 0.76 %
Feγ + Fe3C → Feα + Fe3C
per Xc > 0.76 %
Feγ → Feα + Fe3C
per Xc = 0.76 %
Queste trasformazioni sono fondamentali nel trattamento
termico degli acciai.
La composizione Xc = 0.76·% corrisponde alla miscela
eutettoide.
125
La microstruttura degli acciai eutettoidi (0.76 % di C), è
costituita da un’alternanza di lamelle delle due fasi (α e Fe3C)
che si formano simultaneamente nel corso della
trasformazione.
Questa microstruttura è chiamata perlite.
126
perlite (composizione eutettoidica)
Acciaio ipoeutettoidico
127
Acciaio ipereutettoidico
128
Trasformazioni di fase
Le trasformazioni di fase iniziano con la formazione di un
grande numero di particelle finissime della nuova fase
(nucleazione), che crescono in seguito fino a trasformazione
completa.
Con la formazione della nuova fase, l’energia libera
diminuisce (favorendo il fenomeno) ma la presenza di
un’interfaccia di separazione tra le fasi, il non perfetto
ordinamento degli atomi alla superficie di separazione, i
legami non ancora formati e le deformazioni elastiche e
plastiche la fanno aumentare.
L’accrescimento delle nuove particelle dipende quindi dal
rapporto tra area superficiale e volume; ovvero esiste una
dimensione critica al di sotto della quale esse si ridisciolgono
(embrioni) ed al di sopra della quale crescono (nuclei).
Alla dimensione critica l’energia libera di una particella è
massima: tale energia è la barriera da superare nella cinetica
della nucleazione.
129
Una trasformazione di fase inizia, quindi, su scala submicroscopica: dapprima si formano i nuclei della nuova fase,
con dimensioni dell’ordine di poche centinaia di atomi, ed in
seguito i nuclei crescono fino a che la trasformazione è
completa.
I due principali stadi sono così la nucleazione e
l’accrescimento, che in molti casi possono essere a loro volta
suddivisi in ulteriori stadi.
Ogni stadio ha una propria energia di attivazione: di solito
uno di essi procede più lentamente degli altri e limita la
velocità globale del processo.
La nucleazione può essere omogenea o eterogenea.
130
Nucleazione omogenea
Si consideri, la solidificazione di un metallo puro.
Si supponga, inoltre, che i nuclei abbiano forma sferica,
anche se le conclusioni del procedimento saranno valide per
nuclei di forma qualsiasi.
Se si abbassa bruscamente la temperatura del sistema al di
sotto del punto di fusione, la fase liquida diverrà instabile ed
apparirà una zona di materiale solidificato, la nuova fase
stabile.
La termodinamica prevede che alla stabilità della zona solida
contribuisce una diminuzione di energia libera legata al
volume del nucleo in formazione:
4 3
ΔG v πr Δg v
3
Tuttavia la zona solida è limitata da una superficie, e tale
superficie possiede un’energia libera positiva
∆Gs = 4πr2γ
dove γ è l’energia libera per unità
dell’interfaccia tra il nucleo e la fase liquida.
131
di
superficie
La variazione totale di energia libera per una particella sferica
di raggio r risulterà:
ΔG ΔG s ΔG v 4 πr 2 γ
4 3
πr Δg v
3
Le particelle di raggio minore di r* tenderanno a
ridisciogliersi, diminuendo così la loro energia libera, mentre
le particelle di raggio maggiore di r* diminuiranno la loro
energia libera aumentando le proprie dimensioni.
132
Le particelle subcritiche (r < r*) sono chiamate embrioni e
quelle con raggio maggiore di r* sono chiamate nuclei.
r*
ΔG *
2γ
Δg v
16 πγ3
3Δg V
2
La velocità di nucleazione sarà ovviamente determinata dal
valore ∆G* che a sua volta dipende dalla temperatura ovvero
dal grado di sottoraffreddamento (differenza fra la
temperatura di equilibrio e quella a cui inizia effettivamente
la solidificazione del liquido).
Con semplici passaggi si dimostra che il raggio critico è:
2 γTm
r
ΔH f ΔT
*
Tm = temperatura di fusione
∆Hf = calore latente (entalpia) di fusione
∆T = il sottoraffreddamento.
133
134
135
Diffusione
La diffusione è il meccanismo mediante il quale è possibile
realizzare il trasporto di materia attraverso i solidi.
Tende ad annullare i gradienti di concentrazione.
È attivata dall’energia termica.
Nella maggior parte dei solidi gli atomi sono legati alle loro
posizioni di equilibrio.
L’innalzamento della temperatura provoca l’aumento delle
vibrazioni degli atomi nelle loro posizioni di equilibrio e
l’aumento della concentrazione delle vacanze e dei difetti
cristallini.
Questo fa in modo che una certa percentuale di atomi possa
mettersi in moto attraverso il reticolo cristallino, con due
meccanismi a seconda che prevalga la migrazione attraverso
le vacanze o quella attraverso gli interstizi.
136
137
Leggi di Fick
La diffusione è governata dalle due leggi di Fick
È un processo termodinamicamente spontaneo e come tale
avviene con una diminuzione dell’energia libera e un
aumento di entropia (processo irreversibile).
Una specie A diffonde per un tratto ΔX da una
concentrazione Cs ad una (minore ) Cx.
Il flusso di materia in queste condizioni è dato da:
J x D
dC
dx
Ia legge di Fick
dove D è il coefficiente di diffusione o diffusività.
138
Nel caso in cui la concentrazione della specie diffondente vari
nel tempo siamo in presenza di uno stato transitorio ed il
gradiente dC dx ed il flusso Jx variano nel tempo.
In questo caso vale la IIa legge di Fick:
dC x d dC x
D
dt
dx dx
139
(1)
Nel caso più generale la concentrazione della specie
diffondente Cx varia al variare della distanza x, del tempo t e
della diffusività D. Se D non dipende dalla concentrazione
della specie diffondente (Cx bassa) l’equazione può essere
semplificata:
dC x d 2 C x
D
2
dt dx
(2)
Si dimostra inoltre che in coefficiente di diffusione dipende
dalla temperatura secondo una funzione del tipo Arrhenius:
Ea
D D 0 exp
kT
(3)
dove D0 è il coefficiente a temperatura infinita e Ea l’energia
di attivazione che dipende dal meccanismo interstiziale (0.5 –
1.5 eV) o di vacanze (3 – 5 eV).
140
141
Diagrammi di trasformazione isoterma
Le trasformazioni allo stato solido non avvengono
istantaneamente, in quanto in molti casi è necessaria una
ridistribuzione degli atomi per formare un nuovo reticolo
cristallino.
Esistono parecchi modi di introdurre il parametro tempo.
Il più semplice corrisponde al diagramma di trasformazione
isoterma.
Questo, per una data trasformazione a temperatura costante,
viene ottenuto diagrammando in funzione del tempo la
frazione della nuova fase formata.
In pratica, questo diagramma viene costruito analizzando un
numero sufficiente di campioni portati contemporaneamente
alla temperatura costante prefissata per la trasformazione.
Durante la trasformazione, vengono estratti in successione,
dopo determinati intervalli di tempo, campioni nei quali la
trasformazione viene bloccata, generalmente mediante
raffreddamento istantaneo.
Si osserva poi l’entità della trasformazione avvenuta dopo
ciascun tempo, corrispondente a ciascuno dei campioni
estratti.
142
143
Diagrammi TTT
Conoscendo le isoterme di trasformazione, si possono
calcolare le curve di trasformazione delle fasi in funzione del
tempo e della temperatura (TTT).
Queste curve forniscono il tempo necessario per raggiungere,
ad una data temperatura, un determinato tasso di
trasformazione.
I diagrammi riportano le curve di inizio (zero o 1%) e fine (99
o 100%) trasformazione.
144
Le curve del tempo di trasformazione passano per un minimo
(tmin) ad una temperatura posta tra quella di trasformazione
termodinamica (Te prevista dal diagramma di stato) e 0 K.
Con riferimento alla figura, si scelga una temperatura T1 < Te.
Dopo un raffreddamento rapido del materiale da T > Te a T1
si mantiene il materiale a temperatura costante (T1) e la
trasformazione inizia al tempo t = td per arrestarsi al tempo tf.
Esempi tipici di trasformazioni solido-solido che possono
essere rappresentate mediante l’uso dei diagrammi TTT sono
le trasformazioni degli acciai.
Si consideri per esempio la reazione eutettoide del diagramma
Fe-C:
Raffreddam
ento
γ
α Fe3C
Riscaldamento
La perlite è il prodotto microstrutturale di questa
trasformazione, di cui in figura è mostrata la relativa curva
TTT.
145
Successivamente al raffreddamento rappresentato dal tratto
AB, la trasformazione avviene nel tratto BCD.
La trasformazione da austenite a perlite inizia al punto C e si
completa in 15 s, in corrispondenza del punto D.
La figura riporta anche le microstrutture che si vengono a
formare con il progredire della reazione.
Lo spessore delle lamine dipende dalla temperatura a cui
avviene.
146
A temperature di poco inferiori alla temperatura eutettoide, si
produce una perlite grossolana.
Al diminuire della temperatura la microstruttura diventa più
sottile.
Quando le leghe Fe-C, una volta portate in fase austenitica,
vengono raffreddate rapidamente (temprate) fino ad una
temperatura prossima a quella ambiente, si forma un altro
microcostituente, o fase, detto martensite.
La martensite è una struttura monofasica di non equilibrio che
risulta dalla trasformazione senza diffusione dell’austenite.
Il raffreddamento è talmente veloce da non dare il tempo al
carbonio di uscire dal reticolo cristallino nel quale rimane
intrappolato, formando una soluzione solida interstiziale
sovrassatura di carbonio in ferro-α.
La sua struttura cristallina è una tetragonale corpo centrato,
in pratica una ccc nella quale una dimensione è stata
allungata, nella quale gli atomi di carbonio sono intrappolati
come impurezze interstiziali.
La trasformazione martensitica avviene senza diffusione di
atomi di carbonio all’interno della matrice austenitica e
quindi avviene in modo praticamente istantaneo (alla
velocità del suono).
147
Per questo motivo la trasformazione martensitica è in pratica
indipendente dal tempo (retta orizzontale sul diagramma
TTT).
Infine se un acciaio eutettoidico viene raffreddato
velocemente fino a 550-250 ºC si ottiene una microstruttura
eutettoidica non-lamellare intermedia tra la perlite e la
martensite detta bainite.
148
149
150