Quarta esperienza - Sezione di Fisica

TRASMISSIONE DEL CALORE
(8 novembre 2004)
L’esperienza è finalizzata all’uso operativo di concetti di termologia e alla determinazione
sperimentale di un’importante proprietà termica dei materiali.
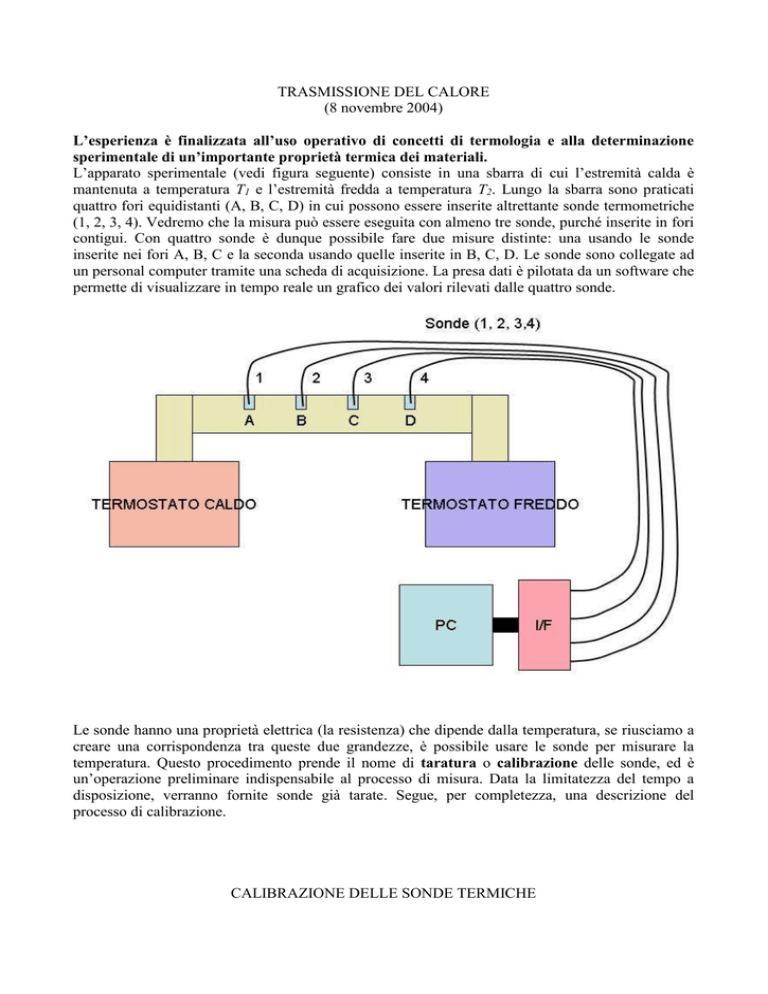
L’apparato sperimentale (vedi figura seguente) consiste in una sbarra di cui l’estremità calda è
mantenuta a temperatura T1 e l’estremità fredda a temperatura T2. Lungo la sbarra sono praticati
quattro fori equidistanti (A, B, C, D) in cui possono essere inserite altrettante sonde termometriche
(1, 2, 3, 4). Vedremo che la misura può essere eseguita con almeno tre sonde, purché inserite in fori
contigui. Con quattro sonde è dunque possibile fare due misure distinte: una usando le sonde
inserite nei fori A, B, C e la seconda usando quelle inserite in B, C, D. Le sonde sono collegate ad
un personal computer tramite una scheda di acquisizione. La presa dati è pilotata da un software che
permette di visualizzare in tempo reale un grafico dei valori rilevati dalle quattro sonde.
Le sonde hanno una proprietà elettrica (la resistenza) che dipende dalla temperatura, se riusciamo a
creare una corrispondenza tra queste due grandezze, è possibile usare le sonde per misurare la
temperatura. Questo procedimento prende il nome di taratura o calibrazione delle sonde, ed è
un’operazione preliminare indispensabile al processo di misura. Data la limitatezza del tempo a
disposizione, verranno fornite sonde già tarate. Segue, per completezza, una descrizione del
processo di calibrazione.
CALIBRAZIONE DELLE SONDE TERMICHE
La calibrazione viene effettuata ponendo in stretto contatto le quattro sonde con un termometro a
mercurio. L’insieme delle sonde e del termometro viene posto in un vaso calorimetrico in cui viene
versata acqua ad una data temperatura. Il software di acquisizione permette di rilevare i conteggi
delle quattro sonde e di inserire manualmente il valore di temperatura letto sul termometro. In tal
modo si è creata una corrispondenza tra la resistenza elettrica delle sonde e un valore della
temperatura. Si ripete l’operazione un certo numero di volte, variando la temperatura dell’acqua (ad
esempio aggiungendo acqua fredda o acqua calda), finché si è raccolto un numero sufficiente di
corrispondenze. E’ buona norma eseguire la taratura cercando di coprire completamente l’intervallo
di temperatura in cui verranno usate le sonde nel processo di misura.
Se durante la misura la sonda viene esposta ad una temperatura che non compare tra quelle di
taratura, un programma presente nel software di acquisizione esegue una interpolazione numerica
con le temperature più vicine.
RICHIAMI DI TERMOLOGIA
Un primo importante concetto è quello di capacità termica, definito come il rapporto tra il calore
scambiato con un oggetto e la sua conseguente variazione di temperatura:
Q
C
.............(1)
T
L’unità di misura è il Joule/Kelvin: J/K.
Se l’oggetto ha una massa m, si definisce il calore specifico come la capacità termica per unità di
massa:
C
c  .............(2)
m
L’unità di misura è il Joule/Kelvin/chilogrammo: J/K/kg.
Un’ultimo richiamo alla legge di Fourier sulla trasmissione del calore per conduzione:
T T
Q  kAt 2 1 .............(3)
x
ove A rappresenta l’area del corpo interessata dal flusso di calore, t l’intervallo di tempo, T2-T1 la
differenza di temperatura tra termostato caldo e termostato freddo, x lo spessore del corpo e k è la
costante di conduzione termica, caratteristica di ogni sostanza.
Da notare il segno meno che garantisce la correttezza del segno del calore scambiato, tenuto conto
del verso naturale (cioè dettato dalla seconda legge della termodinamica) del flusso del calore.
Primo membro: il termostato freddo (quello a temperatura T2) riceve calore e questo corrisponde al
verso naturale di scorrimento, per cui questa quantità di calore è positiva.
Secondo membro: T2 è minore di T1, il segno meno davanti a k rende positivo il secondo membro
dell’equazione.
CONDUZIONE DEL CALORE LUNGO UNA SBARRA
Con riferimento alla figura seguente, supponiamo che i tre punti A, B, C abbiano ascissa (x-x), x e
(x+x) rispettivamente e che il termostato caldo si trovi a sinistra (x=0) e quello freddo a destra
(x=L). Il calore fluirà naturalmente da sinistra a destra (per il secondo principio della
termodinamica), per cui ci sarà una quantità Qin che da A passa a B e una quantità Qout che da B
passa a C. Per la legge di Fourier queste quantità valgono:
Qin  kAt
TB  TA
.............(4)
x
2
Qout  kAt
TC  TB
.............(5)
x
la differenza tra queste quantità di calore rappresenta la quantità di calore trattenuta nell’elemento
B, che vale:
T  TA  2TB
Qtot  Qin  Qout  kAt C
.............(6)
x
Ricordando che un trasferimento netto di calore comporta una variazione di temperatura, possiamo
anche scrivere:
Qtot  cxATB t  t   TB t .............(7)
ove i termini davanti alla parentesi rappresentano la capacità termica dell’elemento B (sono il
prodotto del calore specifico per la densità per il volume). Uguagliando le due ultime espressioni e
riordinando otteniamo:
k TC  T A  2TB TB t  t   TB t 

.............(8)
c
t
x 2
Questa è un’equazione alle differenze finite che descrive il fenomeno della trasmissione del calore
lungo una sbarra.
La costante
k
J
.............(9)
c
è la conducibilità termometrica del materiale. La sua unità di misura è il metroquadrato/secondo:
m2/s.
Facendo il limite perx->0 e t->0, si ottiene l’equazione differenziale seguente:
 2T ( x, t ) T ( x, t )

.............(10)
t
x 2
ove abbiamo usato il simbolo di derivata parziale, in quanto la temperatura T è funzione di due
variabili: x e t.
J
L’ESPERIMENTO VERO E PROPRIO
3
Una prima considerazione: lo sviluppo teorico precedente ci indica che non misureremo la costante
k, ma piuttosto la costante J. Questo non è ovviamente un problema, perché k può essere ricavato
dall’equazione (9) una volta che siano noti J,  e c.
Nella figura seguente è riportato un andamento tipico delle misure di temperatura nel tempo per tre
punti lungo la sbarra:
La seconda considerazione: è possibile misurare J solo se si studia il sistema in situazione non
stazionaria, cioè uno stato che dipenda dal tempo. Infatti in caso contrario il secondo membro della
(8) o della (9) vanno a zero e nel primo membro si può semplificare la costante J, che quindi
scompare dall’equazione.
Notiamo che l’equazione (8) è un’approssimazione della (10) e il suo uso sarà tanto più giustificato
quanto più la funzione T(x,t) è lineare rispetto alle sue variabili. Dall’esame dell’andamento di T in
funzione del tempo, si nota che il grafico presenta un punto di flesso. In tale punto, T è ben
approssimabile linearmente, per cui l’istante di tempo corrispondente è il migliore per applicare la
formula (8). Il punto di flesso si può trovare nel modo seguente: si prendono i dati di temperatura e
con un algoritmo alle differenze finite (ad esempio usando Excel) si calcola la ‘derivata’ dei dati di
temperatura. Il punto di flesso per i dati di temperatura corrisponde al punto di massimo per i dati
della derivata della temperatura. Per eliminare le fluttuazioni casuali nella determinazione del
massimo, è bene ‘lisciare’ un po’ i dati (usando il grafico è sufficiente farlo a occhio, altrimenti si
potrebbe usare un procedimento di fit) e trovarne l’andamento medio.
Per ragioni di precisione di calcolo numerico, alla (8) si preferisce un’equazione simmetrizzata
rispetto all’istante t. Per ottenere questa equazione basta riscrivere la (8) per un valore negativo di
t e farne la semisomma con la (8) stessa:
J
TC  TA  2TB TB t  t   TB t  t 

.............(11)
2t
x 2
4
Per calcolare J bisogna scegliere un opportuno istante t (vedi figura precedente), e cinque valori di
temperatura: nei punti A e C all’istante t e nel punto B agli istanti t, t-t e t+t. Bisogna inoltre
misurare la distanza x tra i punti, mediante un calibro, e ricordare il valore t scelto come
intervallo di campionatura.
DETERMINAZIONE DELL’ERRORE SU J
Risolviamo la (11) rispetto a J:
TB t  t   TB t  t 
N
2t
J
 .............(12)
TC  TA  2TB
D
2
x
ove per semplicità si è indicato il numeratore e il denominatore rispettivamente con N e D.
Applichiano la formula di propagazione dell’errore relativo:
 (J )
J

 (N )
N

 ( D)
D
.......... ....(13)
Indicando con TB1 e TB2le temperature nel punto B agli istanti t+ t e t-t, rispettivamente,
l’errore su N è dato da:
 (N ) 


N
N
N
 (T B1 ) 
 (T B 2 ) 
 (t )
TB1
TB 2
t
T T
1
1
 (T B1 ) 
 (T B 2 )  B1 B2  (t ) 
2 t
2 t
2 t 2
 (T B )
t
................................................................................(14)
ove nell’ultimo passaggio si è supposto che gli errori sulle temperature siano uguali e che l’errore
sull’intervallo di campionamento sia trascurabile.
L’errore su D è:
 ( D) 


1
x
2
4
x
2
D
D
D
D
 (TC ) 
 (T A ) 
 (TB ) 
 (x) 
TC
T A
TB
x
 (TC ) 
 (T )  2
1
x
2
 (T A ) 
2
x
2
 (TB )  2
TC  T A  2TB
x
3
 (x) 
D
 (x)......... .......... .......... .......... .......... .......... .......... .......... ..(15)
x
dove è stata fatta la stessa supposizione sugli errori di temperatura. Le formule (13), (14) e (15)
bastano a determinare l’errore su J.
5