Diapositiva 1 - Facolta di Ingegneria

Sistema strutturale
Corso di Costruzioni in zona sismica
Laurea Magistrale in Ingegneria Civile
Università del Salento
LA CONCEZIONE STRUTTURALE
Marianovella Leone
Anno Accademico 2012/2013
Prof.ssa Maria Antonietta Aiello
La concezione strutturale
Il progetto strutturale dovrebbe accompagnare sin dall’inizio l’ITER PROGETTUALE
Un progetto INTELLIGENTE tiene in debito conto delle esigenze strutturali
ESIGENZE STRUTTURALI
ESIGENZE FUNZIONALI
PROGETTO
ARCHITETTONICO
ESIGENZE IMPIANTISTICHE
In REALTA’?....
Il momento del progetto strutturale si concretizza nella fase esecutiva, nel momento in cui ottenuta la
concessione sulla base di un progetto che definisce le FORME e le FUNZIONI si deve realizzare
l’edificio…
I tempi lunghi e la rigidità amministrativa che si incontrano pongono un limite serio alle possibili modifiche a
causa di problemi strutturali
GRAVI VINCOLI
PROGETTAZIONE NON
RAZIONALE
La concezione strutturale
Gli aspetti fondamentali in una corretta concezione strutturale sono:
•
Rigidezza e resistenza flessionali secondo due direzioni;
•
Rigidezza e resistenza torsionali;
•
Rigidezza e resistenza dei solai;
•
Fondazioni adeguate;
•
Regolarità;
•
Iperstaticità;
•
Semplicità strutturale e simmetria;
RIGIDEZZA E RESISTENZA FLESSIONALI SECONDO DUE DIREZIONI
Assicurano un buon comportamento della struttura qualunque sia la direzione del moto sismico. La presenza di due sistemi
resistenti orditi secondo due direzioni ortogonali e aventi valori di rigidezza simili è estremamente importante se si considera
l’impossibilità di prevedere la direzione di azione del sisma.
La concezione strutturale
RESISTENZA E RIGIDEZZA TORSIONALI
Assicurano limitati effetti torsionali nella struttura e quindi riducono il rischio che spostamenti differenziali, dovuti a tali effetti nei
diversi elementi strutturali, inducano sollecitazioni non uniformi.
RESISTENZA E RIGIDEZZA DEI SOLAI DEL PIANO
Assicurano capacità di ridistribuzione delle forze indotte dal sisma sul sistema proporzionalmente alla rigidezza e resistenza e un
comportamento globale uniforme.
Predimensionamento: si possono ritenere valide le prescrizioni del D.M. ‘96
(spessore non inferiore a 1/25 della luce o 1/30 nel caso di
nervature precompresse)
Deve adottarsi uno spessore con soletta di almeno 40 mm
con armatura di ripartizione ben ancorata alle travi di bordo.
Si richiede un incremento di spessore nel caso le prescrizioni
architettoniche richiedono luci superiori ai 5 m senza impiego
di travi emergenti
Sotto queste ipotesi il solaio può essere considerato RIGIDO.
La concezione strutturale
FONDAZIONI ADEGUATE
Assicurano un’eccitazione sismica uniforme, riducendo il rischio di eventuali spostamenti dovuti a input asincrono. Il sistema
dovrà essere dotato di adeguata rigidezza nel piano e adeguata rigidezza flessionale. Dovrà essere adottata una sola tipologia di
fondazione per una data struttura in elevazione, a meno che la struttura stessa non consista di più unità indipendenti.
IPERSTATICITA’
Assicura una più ampia ridistribuzione degli effetti dell’azione sismica e dissipazione di energia
La concezione strutturale
REGOLARITA’ E SIMMETRIA
Risposta globale uniforme, si riducono le concentrazioni di sforzi e di elevata richiesta di duttilità
La concezione strutturale
SEMPLICITA’ STRUTTURALE
Assicura l’esistenza di percorsi evidenti e diretti per la trasmissione delle forze sismiche riducendo le incertezze insite nelle varie
fasi di progettazione ed esecuzione e rende quindi più affidabile la previsione del comportamento della struttura soggetta al
sisma.
La concezione strutturale
ATTENZIONE A PARTICOLARI DISPOSIZIONI
Sistema strutturale
Sistema strutturale
STRUTTURE A PARETI
Sono di due tipi: a pareti semplici o accoppiate
Una parete accoppiata consiste di due o più pareti semplici collegate tra loro ai piani dell’edificio da travi di collegamento
disposte in modo regolare lungo l’altezza.
Sotto azioni laterali si comportano come una mensola. Gli
spostamenti relativi dei piani derivano dalla deformazione
flessionale dei muri e quindi presentano una forma convessa
dalla parte dei carichi.
La distribuzione del taglio è proporzionale al momento di inerzia
della sezione dei muri.
Sistema strutturale
STRUTTURE A PARETI
Limite: Essendo sistemi molto rigidi possono sopportare notevoli azioni sismiche a fronte però di elevati momenti alla base.
Questo comporta che la richiesta di duttilità locale in corrispondenza della base sia elevata e quindi che la crisi venga raggiunta a
causa di un danno concentrato e non, come preferibile, a causa di un danno distribuito. Richiedono inoltre un impegno molto più
oneroso per le fondazioni.
Predimensionamento: Le azioni verticali e quelle orizzontali dovute al sisma possono essere trattate separatamente. Le pareti
devono essere disposte in modo regolare nell’edificio
Sistema strutturale
STRUTTURE MISTA PARETI-TELAIO
In questo tipo di strutture la resistenza alle azioni verticali è affidata prevalentemente ai telai; la resistenza alle azioni
orizzontali è affidata in parte ai telai ed in parte alle pareti
A causa dell’iterazione dei due sistemi, la risposta del sistema
accoppiato altera i diagrammi di taglio e momento di entrambi.
In particolare, nei piani più bassi il muro vincola il telaio
limitandone le deformazioni, mentre nella parte superiore è il
telaio a limitare gli spostamenti del muro.
Sistema strutturale
STRUTTURE MISTA PARETI-TELAIO
Anche in questi edifici si possono verificare condizioni di elevato rischio di concentrazioni di danno o di rottura fragile. Oltre a
dover fare particolare attenzione alle fondazioni, si possono verificare rotture localizzate nei casi di discontinuità del muro al di
sopra o al di sotto di un certo piano.
Sistema strutturale
STRUTTURE A TELAIO
E’ la tipologia costruttiva maggiormente diffusa, le sollecitazioni sia di natura statica che dinamica sono affidate alle travi e ai
pilastri che costituiscono l’ossatura portante.
Il primo passo da fare quando si inizia a progettare una struttura è quello relativo all’impostazione della carpenteria, in tale
operazione i principi fondamentali da rispettare sono i seguenti:
a)
Per compensare parzialmente l’incremento di sollecitazioni sulle travi dovute al sisma, è bene ridurre l’effetto dei carichi
verticali adottando, sia per le travi che per i solai e gli sbalzi, delle luci ridotte rispetto a quelle consigliate i assenza di sisma;
b)
È bene evitare la disuniformità di luci delle travi. Essa infatti è negativa in quanto causa concentrazioni di sollecitazioni
nelle campate più corte. Se è necessario adottare luci differenti è bene ridurre la rigidezza delle travi nelle campate più corte
utilizzando travi a spessore.
c)
È bene evitare una forte disuniformità di carico verticale sui pilastri. Essa infatti comporta la necessità di sezioni maggiori,
e quindi concentrazioni di azioni sismiche.
Sistema strutturale
STRUTTURE A TELAIO
Una corretta impostazione della carpenteria dovrebbe garantire un irrigidimento uniforme in entrambe le direzioni.
In realtà questa regolarità risulta fortemente virtuosa in termini di risposta sismica, e la normativa permette per questo tipo
di strutture una analisi semplificata rispetto a quella dinamica modale, obbligatoria per le strutture cosiddette irregolari.
Sistema strutturale
STRUTTURE A TELAIO
Nell’ambito della carpenteria si dovranno individuare quali sono le travi destinate a portare i solai, che saranno quindi soggette
a consistenti carichi verticali oltre a fungere da traversi dei telai sismo-resistenti.
In una progettazione di soli carichi verticali la convenienza economica a minimizzare il numero di travi porta
necessariamente a mantenere il più possibile costante l’orditura dei solai. Al contrario la necessità di disporre
in zona sismica di una doppia orditura di travi porta alcuni progettisti alla scelta di variare continuamente
l’orditura dei solai.
Anche se in tal modo si può ottenere una più uniforme distribuzione dei carichi sulle travi, si ritiene che tale
scelta comporti complicazioni esecutive tali da rendere gli svantaggi prevalenti rispetto ai vantaggi.
Sistema strutturale
STRUTTURE A TELAIO
Nella scelta degli elementi strutturali si osservi che le travi alte costituiscono un efficace controvento per i
pilastri che se vincolati a travi a spessore potrebbero risentire di un deficit di rigidezza trasversale.
Un pilastro con travi a spessore fornisce un contributo relativamente basso in termini di rigidezza ai piani
superiori al primo, che invece risente dell’incastro della fondazione, pertanto si prevedono in tali casi elevati
spostamenti di interpiano crescenti dal basso verso l’alto sotto azione sismica.
Anche pilastri troppo esili (bassa rigidezza sezionale) sono sconsigliabili per lo stesso motivo.
Sistema strutturale
STRUTTURE A TELAIO
In caso di carpenterie eccessivamente irregolari si consiglia l’adozione di giunti per rendere la struttura maggiormente regolare.
GIUNTI
Sistema strutturale
STRUTTURE A TELAIO: Predimensionamento del solaio
Si possono ritenere valide le prescrizioni del D.M. 1996 (spessore non inferiore a 1/25 della
luce o 1/30 nel caso di nervature precompresse)
Deve adottarsi uno spessore con soletta di almeno 40 mm con armatura di ripartizione ben
ancorata alle travi di bordo
Si richiede un incremento di spessore nel caso le prescrizioni architettoniche richiedano luci
superiori ai 5 m senza impiego di travi emergenti
Il solaio nella analisi statica equivalente è considerato un impalcato con rigidezza
infinita.
Sistema strutturale
STRUTTURE A TELAIO: Predimensionamento travi
TRAVI A SPESSORE
Si consideri che l’effetto del sisma sulle travi a spessore è modesto se sono presenti travi emergenti nel telaio
pertanto nel predimensionamento ci si può basare sui soli carichi verticali.
Le travi di collegamento, parallele all’orditura del solaio e quindi poco caricate, avranno dimensioni ridotte
dettate principalmente da motivazioni geometriche (per esempio la larghezza può essere pari a 60 cm, ottenuti
eliminando dal solaio una fila di laterizi).
ATTENZIONE!
Se l’edificio è tutto con travi a spessore, esse collaborano alla resistenza sismica, ed essendo meno duttili
rispetto alle travi alte (CD-B obbligata!) è consigliabile partire con solaio H=25+5 in zona sismica anche per
luci non richiedenti tali prescrizioni sotto le sole azioni verticali
Sistema strutturale
STRUTTURE A TELAIO: Predimensionamento travi
TRAVI A SPESSORE
In caso di trave portante una regola grossolana (in condizioni statiche) consente di dimensionare la base come:
B= L/6
Nella pratica la larghezza della trave a spessore varia tra 60 e 120 cm. È opportuno limitare la larghezza della sezione e
concentrare le armature in un fascio di ampiezza comparabile a quella del pilastro. Indicazioni legate a problemi di duttilità.
ATTENZIONE: Le NTC 08 impongono limitazioni alla massima larghezza della trave.
Sistema strutturale
STRUTTURE A TELAIO: Predimensionamento travi
TRAVI EMERGENTI
Si consideri che l’effetto del sisma (sollecitazioni flesso-taglianti) sulle travi alte è molto sentito, specialmente
nei piani bassi, e talvolta anche in quelli centrali del fabbricato. Ad esempio in fabbricati di 4-6 impalcati dette
sollecitazioni hanno entità maggiore rispetto a quelle provocate dai carichi verticali.
Nella stima della sollecitazione sismica si ricordi che i carichi statici fanno crescere le sollecitazioni
all’aumentare della luce, i carichi sismici fanno crescere le sollecitazione all’aumentare della rigidezza
(riduzione della luce!)
-
In linea di massima la base della trave è pari al lato del pilastro
-
Una regola grossolana per dimensionare l’altezza di una trave portante
in condizioni statiche è:
H=L/(10÷12)
DUNQUE: L’azione del sisma è maggiormente sentita nelle campate corte ed in prossimità dei pilastri più
rigidi
Sistema strutturale
STRUTTURE A TELAIO: Predimensionamento travi
TRAVI EMERGENTI
È buona norma adottare sezioni delle travi molto simili a quelle dei pilastri, in modo da non alterare la
regolare distribuzione di sollecitazione flettente lungo i pilastri.
Sezioni delle travi molto più piccole di quelle dei pilastri sposterebbero il punto di nullo del
momento flettente dalla mezzeria dei pilastri e dunque si avrebbe un M maggiore a parità di taglio
sui pilastri.
Viceversa se la sezione delle travi è molto più grande si violerebbe il principio di gerarchia delle
resistenze incentivando un comportamento fragile della struttura.
Una buona indicazione è quella per edifici di 4-5 impalcati di adottare dimensioni pari a
30x60/30x50 cm.
Sebbene le sollecitazioni si riducano all’aumentare dell’altezza è bene non ridurre la sezione per non
ridurre la rigidezza trasversale dei pilastri che in quelle zone risentono delle maggiori deformazioni.
Sistema strutturale
STRUTTURE A TELAIO: Predimensionamento travi
La differenza tra l’utilizzo di travi alte e a spessore si può notare già dal differente comportamento per carichi non sismici.
Trave a spessore
Trave emergente
Il momento agente agli appoggi della trave risulta notevolmente ridotto, di conseguenza anche il momento sul pilastro lo sarà.
La stessa cosa si può dire per il taglio.
Sistema strutturale
STRUTTURE A TELAIO: Predimensionamento travi
In presenza di azione sismica l’influenza della presenza di travi a spessore o emergenti si fa ancora più evidente
Trave a spessore
1
88
111
77
122
78
Trave emergente
24
55
Sistema strutturale
STRUTTURE A TELAIO: Predimensionamento travi
TELAIO SHEAR – TYPE
Travi con rigidezza flessionale infinita
Travi con rigidezza assiale infinita
Travi con rigidezza a taglio infinita
Pilastri con rigidezza assiale infinita
Conseguenza:
In virtù della infinita rigidezza assiale dei pilastri, i traversi sono impediti di ruotare rigidamente.
Inoltre, per la infinita rigidezza assiale e flessionale dei traversi, questi stessi non possono deformarsi
assialmente o flessionalmente.
Sistema strutturale
STRUTTURE A TELAIO: Predimensionamento travi
TELAIO SHEAR – TYPE
Il momento che si genera nei pilastri ha un andamento a farfalla
Sistema strutturale
STRUTTURE A TELAIO: Predimensionamento travi
TELAIO SHEAR – TYPE
Il taglio nel generico pilastro è legato allo spostamento relativo di piano
Essendo lo spostamento di piano uguale per tutti i pilastri, il taglio di
piano si ottiene dalla sommatoria di tutti i tagli agenti sui pilastri
Sistema strutturale
STRUTTURE A TELAIO: Predimensionamento travi
TELAIO SHEAR – TYPE
Il sistema di telaio shear-type approssima bene il comportamento di pilastri collegati da travi emergenti di elevata altezza e
modesta luce
Il sistema di telaio shear-type multipiano si comporta come un insieme di sistemi monopiano posti in serie
Sistema strutturale
STRUTTURE A TELAIO: Predimensionamento travi
TELAIO SHEAR – TYPE
Il sistema con travi infinitamente flessibili si comporta come un insieme di mensole incastrate alla base.
Esso approssima bene il comportamento di pilastri collegati da travi a spessore di luce elevata.
ESEMPI DI SCELTE STRUTTURALI E PROGETTUALI
Nella pratica progettuale si può concludere che:
IN PRESENZA DI TRAVI SPESSORE
Le travi soggette a sisma subiscono rispetto al caso dei soli carichi verticali un lieve incremento di M e T
I pilastri subiscono lievi incrementi di sforzo assiale e rilevanti incrementi di momento flettente ai piani
bassi.
Nel predimensionamento delle travi ci si può riferire ai soli carichi verticali
Per i pilastri deve considerarsi un più gravoso regime di pressoflessione specialmente nei piani bassi.
IN PRESENZA DI TRAVI ALTE
Le travi soggette a sisma subiscono rispetto al caso dei soli carichi verticali dei SENSIBILI incrementi di M
e T crescenti dai piani alti a quelli bassi
I pilastri subiscono rilevanti variazioni di sforzo assiale e rilevanti incrementi di momento flettente
proporzionali alle sollecitazioni taglianti ; le azioni orizzontali hanno distribuzione triangolare, i tagli hanno
distribuzione trapezoidale
Nel predimensionamento delle travi ci si può riferire ai soli carichi verticali
Per i pilastri deve considerarsi un più gravoso regime di pressoflessione specialmente nei piani bassi.
ESEMPI DI SCELTE STRUTTURALI E PROGETTUALI
DM 14 Gennaio 2008
Nella concezione dell’edificio il progetto architettonico influisce sensibilmente su un parametro che risulta
determinante nell’analisi del comportamento sismico: LA REGOLARITA’.
Un edificio si considera REGOLARE se rispetta i requisiti di regolarità in pianta ed in altezza. Dal
rispetto di tali requisiti dipende la capacità dell’organismo strutturale di rispondere globalmente al sisma con
un regime più o meno favorevole di azioni interne (sollecitazioni), e di evitare pericolose concentrazioni di
sforzi che richiederebbero sovra-resistenze economicamente non sostenibili o materialmente irraggiungibili
attraverso la geometria prescelta.
Sistema strutturale
STRUTTURE A TELAIO: Predimensionamento pilastri
-
In zona sismica i pilastri sono dimensionati a pressoflessione considerando il dominio M-N
- Il valore massimo che può essere portato da una sezione corrisponde ad uno sforzo normale Ned per il quale la tensione media
Ned/Ac è all’incirca 0,5 fcd
- Aumentare N sui pilastri significa anche diminuire la loro capacità di rotazione
>B ~Mrd uguale
ATTENZIONE: Aumentando la base non
conferisce un significativo beneficio in termini di
resistenza flessionale, al contrario, aumentando
l’altezza si incrementa di molto la resistenza
flessionale.
….MA…..aumentare l’altezza vuol dire anche
incrementare sensibilmente la rigidezza
flessionale e dunque anche la sollecitazione
sismica!
>H = >K ma > richiesta sismica
Sistema strutturale
STRUTTURE A TELAIO: Predimensionamento pilastri
Per tenere in conto le precedenti osservazioni, nella fase di predimensionamento di può procedere assumendo un limite massimo
per la tensione media nei pilastri, in particolare si consiglia di non superare il valore di 0,5fcd e di mantenersi prossimi a 0,3-0,4
fcd.
Per un CLS di classe C25/30 si limita la tensione tra 4.0 e 5.5 MPa
Per un CLS di classe C20/25 si limita la tensione tra 3.5 e 4.5 MPa
In fase di predimensionamento si può effettuare una analisi statica senza
sisma nel caso in cui siano state evitate travi molto corte e rigide.
Si determina in questo modo l’area necessaria di cls considerando la
tensione massima ridotta.
Sistema strutturale
STRUTTURE A TELAIO: Predimensionamento pilastri
Anche le NTC impongono un limite alla massima sollecitazione di compressione:
7.4.4.2.1
Sistema strutturale
STRUTTURE A TELAIO: Predimensionamento pilastri
Anche le NTC impongono un limite alla massima sollecitazione di compressione:
Se la carpenteria è regolare si avranno sezioni dei pilastri tutte uguali, altrimenti, pur potendo adottare sezioni differenti, si
consiglia di sovradimensionare i pilastri meno caricati. In questo modo si ottiene uno sgravio flessionale dei pilastri più caricati.
Bisogna far attenzione alla riduzione delle sezioni ai piani
superiori, si potrebbero avere problemi esecutivi nei nodi che
inficiano la trasmissione delle sollecitazioni.
Per edifici non troppo alti si consiglia di non adottare riduzioni
di sezioni o comunque limitare le riseghe sia come numero
(invariata per almeno 2 ordini ) che come entità.
ESEMPI DI SCELTE STRUTTURALI E PROGETTUALI
L’assorbimento delle azioni orizzontali dipende sensibilmente dalla presenza di travi
emergenti o travi a spessore di solaio.
Si consideri un telaio in zona sismica ed uno in zona non sismica:
Colonne 30x30 cm – Trave 30x50 cm
ESEMPI DI SCELTE STRUTTURALI E PROGETTUALI
1° IPOTESI DI TRAVERSO DEFORMABILE:
Nel telaio sismico il primo pilastro si scarica ed il secondo incrementa sensibilmente
le sollecitazioni
Momento flettente
ESEMPI DI SCELTE STRUTTURALI E PROGETTUALI
Nel telaio sismico il primo pilastro si scarica ed il secondo incrementa sensibilmente
le sollecitazioni
29 kN
69 kN
Taglio
ESEMPI DI SCELTE STRUTTURALI E PROGETTUALI
Nel telaio sismico il primo pilastro si scarica ed il secondo incrementa sensibilmente
le sollecitazioni
120 kN
143 kN
Sforzo assiale
ESEMPI DI SCELTE STRUTTURALI E PROGETTUALI
2° IPOTESI DI TRAVERSO INFINITAMENTE RIGIDO:
Se l’impalcato può considerarsi infinitamente rigido rispetto alle colonne allora la
presenza del sisma non modifica la sollecitazione flettente sul traverso.
In realtà il comportamento reale dei telai è intermedio tra quello con travi infinitamente
rigide (telai shear-type) e quello con travi deformabili
Influenza delle scelte progettuali
Per valutare l’influenza delle scelte progettuali sulla distribuzione delle sollecitazioni nella struttura si esamineranno diversi
esempi applicativi.
1° CASO: Impalcato rigido con travi a spessore 70x25 e pilastri 40x40 al piano terra e 30x30 al primo,
secondo e terzo piano.
2° CASO: Impalcato rigido con travi emergenti 30x55 e pilastri 40x40 al piano terra e 30x30 al
primo, secondo e terzo piano.
3° CASO: Impalcato non rigido con travi emergenti 30x55 e pilastri 40x40 al piano terra e 30x30 al primo,
secondo e terzo piano.
4° CASO: Impalcato non rigido con travi emergenti 30x55 e pilastri 60x60 al piano terra e 40x40 al piano
primo, secondo e terzo.
5° CASO: Campate irregolari con travi a spessore nelle campate corte ed emergenti nelle campate lunghe.
6° CASO: Campate irregolari con travi emergenti in tutte le campate.
Influenza delle scelte progettuali
Per valutare l’influenza delle scelte progettuali sulla distribuzione delle sollecitazioni nella struttura si esamineranno diversi
esempi applicativi.
1° CASO: Impalcato rigido con travi a spessore 70x25 e pilastri 40x40 al piano terra e 30x30 al primo,
secondo e terzo piano.
2° CASO: Impalcato rigido con travi emergenti 30x55 e pilastri 40x40 al piano terra e 30x30 alprimo,
secondo e terzo piano.
3° CASO: Impalcato non rigido con travi emergenti 30x55 e pilastri 40x40 al piano terra e 30x30 al primo,
secondo e terzo piano.
4° CASO: Impalcato non rigido con travi emergenti 30x55 e pilastri 60x60 al piano terra e 40x40 al piano
primo, secondo e terzo.
5° CASO: Campate irregolari con travi a spessore nelle campate corte ed emergenti nelle campate lunghe.
6° CASO: Campate irregolari con travi emergenti in tutte le campate.
Influenza delle scelte progettuali
Confronto tra 1 CASO (travi a spessore) e 2 CASO (travi emergenti)
Influenza delle scelte progettuali
Confronto tra 1 CASO e 2 CASO: Diagramma del momento
Mmax pilastri (travi spessore) = 520 kNm
Mmax pilastri (travi emergenti)= 320 kNm
Riduzione del 39%
Con le travi emergenti diminuisce la
sollecitazione nei pilastri e aumenta
nelle travi. La luce di taglio si sposta
all’incirca in mezzeria.
Influenza delle scelte progettuali
Confronto tra 1 CASO e 2 CASO: Diagramma del taglio
Tmax pilastri (travi spessore) = 230 kN
Tmax pilastri (travi emergenti)= 210 kN
I diagrammi risultano simili e non vi
è una grande differenza in termini
numerici.
Influenza delle scelte progettuali
Confronto tra 1 CASO e 2 CASO: Deformata
∆ max (travi spessore) = 2.82 cm
∆ max (travi emergenti) = 0.98 cm
In termini di deformazione il telaio con
travi a spessore risulta più deformabile
Influenza delle scelte progettuali
Per valutare l’influenza delle scelte progettuali sulla distribuzione delle sollecitazioni nella struttura si esamineranno diversi
esempi applicativi.
1° CASO: Impalcato rigido con travi a spessore 70x25 e pilastri 40x40 al piano terra e 30x30 al primo,
secondo e terzo piano.
2° CASO: Impalcato rigido con travi emergenti 30x55 e pilastri 40x40 al piano terra e 30x30 al
primo, secondo e terzo piano.
3° CASO: Impalcato non rigido con travi emergenti 30x55 e pilastri 40x40 al piano terra e 30x30 al primo,
secondo e terzo piano.
4° CASO: Impalcato non rigido con travi emergenti 30x55 e pilastri 60x60 al piano terra e 40x40 al piano
primo, secondo e terzo.
5° CASO: Campate irregolari con travi a spessore nelle campate corte ed emergenti nelle campate lunghe.
6° CASO: Campate irregolari con travi emergenti in tutte le campate.
Influenza delle scelte progettuali
Confronto tra 2 CASO (impalcato rigido) e 3 CASO (impalcato non rigido): Diagramma del momento
Mmax pilastri (rigido) = 320 kNm
Mmax pilastri (deformabile)= 390 kNm
Riduzione del 18%
Con l’ipotesi di impalcato rigido e
assumendo sempre travi emergenti
il momento sui pilastri risulta superiore
al caso di solaio flessibile.
Influenza delle scelte progettuali
Confronto tra 2 CASO e 3 CASO: Diagramma del taglio
Tmax pilastri (caso 2) = 210 kN
Tmax pilastri (caso 3)= 230 kN
I diagrammi risultano simili e non vi
è una grande differenza in termini
Numerici.
Influenza delle scelte progettuali
Confronto tra 2 CASO e 3 CASO: Deformata
∆ max (rigido) = 0.98 cm
∆ max (deformabile) = 1.32 cm
In termini di deformazione il telaio con
implacato non rigido risulta più
deformabile
Influenza delle scelte progettuali
Per valutare l’influenza delle scelte progettuali sulla distribuzione delle sollecitazioni nella struttura si esamineranno diversi
esempi applicativi.
1° CASO: Impalcato rigido con travi a spessore 70x25 e pilastri 40x40 al piano terra e 30x30 al primo,
secondo e terzo piano.
2° CASO: Impalcato rigido con travi emergenti 30x55 e pilastri 40x40 al piano terra e 30x30 al
primo, secondo e terzo piano.
3° CASO: Impalcato non rigido con travi emergenti 30x55 e pilastri 40x40 al piano terra e 30x30 al primo,
secondo e terzo piano.
4° CASO: Impalcato non rigido con travi emergenti 30x55 e pilastri 60x60 al piano terra e 40x40 al piano
primo, secondo e terzo.
5° CASO: Campate irregolari con travi a spessore nelle campate corte ed emergenti nelle campate lunghe.
6° CASO: Campate irregolari con travi emergenti in tutte le campate.
Influenza delle scelte progettuali
Confronto tra 3 CASO e 4 CASO: Diagramma del momento
Mmax pilastri (pilastri «piccoli») = 390 kNm
Mmax pilastri (pilastri «grandi»)= 535 kNm
Riduzione del 27%
Un eccessivo aumento della sezione dei
pilastri comporta un aumento del
momento a causa del notevole incremento
di rigidezza.
Influenza delle scelte progettuali
Confronto tra 3 CASO e 4 CASO: Deformata
∆ max (pilastri «piccoli») = 1.32 cm
∆ max (pilastri «piccoli») = 1.32 cm
In termini di deformazione non si
hanno notevoli differenze
Influenza delle scelte progettuali
Per valutare l’influenza delle scelte progettuali sulla distribuzione delle sollecitazioni nella struttura si esamineranno diversi
esempi applicativi.
1° CASO: Impalcato rigido con travi a spessore 70x25 e pilastri 40x40 al piano terra e 30x30 al primo,
secondo e terzo piano.
2° CASO: Impalcato rigido con travi emergenti 30x55 e pilastri 40x40 al piano terra e 30x30 al
primo, secondo e terzo piano.
3° CASO: Impalcato non rigido con travi emergenti 30x55 e pilastri 40x40 al piano terra e 30x30 al primo,
secondo e terzo piano.
4° CASO: Impalcato non rigido con travi emergenti 30x55 e pilastri 60x60 al piano terra e 40x40 al piano
primo, secondo e terzo.
5° CASO: Campate irregolari con travi a spessore nelle campate corte ed emergenti nelle campate lunghe.
6° CASO: Campate irregolari con travi emergenti in tutte le campate.
Influenza delle scelte progettuali
Confronto tra 5 CASO e 6 CASO:
LUCI IRREGOLARI
3
6
7
6
3
Influenza delle scelte progettuali
Confronto tra 5 CASO e 6 CASO:
Emergenti + spessore
Emergenti
Influenza delle scelte progettuali
Confronto tra 5 CASO e 6 CASO: Diagramma del momento
Mmax pilastri (E+S) = 445 kNm
Mmax pilastri (E)= 395 kNm
Riduzione del 11%
La variazione di sezione delle travi comporta
una variazione delle sollecitazioni nei pilastri,
Nelle campate centrali si hanno sollecitazioni
maggiori nel caso di presenza agli estremi
di travi a spessore
Influenza delle scelte progettuali
Confronto tra 5 CASO e 6 CASO: Deformata
∆ max (E+S) = 1.69 cm
∆ max (E) = 1.34 cm
In termini di deformazione non si
hanno notevoli differenze
CONSIGLI PRATICI PER LA PROGETTAZIONE ARCHITETTONICA
Nell’impostazione per carichi verticali:
• Adottare per le luci di sbalzi, solai e travi dimensioni non eccessive, si
consigliano le seguenti:
CONSIGLI PRATICI PER LA PROGETTAZIONE ARCHITETTONICA
• Evitare campate di trave troppo corte, che provocherebbero concentrazione di
sollecitazioni
•Evitare strutture composte da telai e pareti in muratura portante
CONSIGLI PRATICI PER LA PROGETTAZIONE ARCHITETTONICA
•Evitare parapetti rigidi in strutture intelaiate
•Evitare travi tozze
CONSIGLI PRATICI PER LA PROGETTAZIONE ARCHITETTONICA
•Evitare singoli piani superiori o piano terra con bassa rigidezza
•Evitare sistemi di controvento non simmetrici
CONSIGLI PRATICI PER LA PROGETTAZIONE ARCHITETTONICA
•Evitare spostamenti dei sistemi di controvento
•Cercare di orientare i pilastri, per quanto possibile, per il 50% in una
direzione e per il 50% nella direzione ortogonale in modo da
centrifugare le rigidezze.
PRIME ANALISI DELL’EDIFICIO
Tipologia: Edificio adibito a OSPEDALE
Struttura portante principale:
In cemento armato con struttura intelaiata.
Materiali: calcestruzzo C35/45
acciaio B450C
Altezze d’interpiano: 3.50 m a tutti i piani
PRIME ANALISI DELL’EDIFICIO
Le caratteristiche meccaniche del conglomerato cementizio armato sono definite in funzione del
valore caratteristico della resistenza cilindrica fck:
Il primo termine rappresenta la
resistenza cilindrica a compressione
fck, mentre il secondo la Rck,
resistenza cubica a compressione.
Es:
C 35/45 possiede:
fck=35 [N/mm^2]
Rck =45 [N/mm^2]
PRIME ANALISI DELL’EDIFICIO
PRIME ANALISI DELL’EDIFICIO
CARATTERISTICHE DEL CLS (E.C. 2) e NTC 2008
PRIME ANALISI DELL’EDIFICIO
Classe utilizzata nel progetto C35/45 :
fcd=0.85*35/1.5 [N/mm^2]= 19.83 [N/mm^2]
per classi < C50/60
fctm = 0,30×fck^2/3 =3.21 [N/mm^2]
fctk_0.05 = 1.3×fctm =4.17 [N/mm^2]
fctk_0.05 = 0,7×fctm =2.24 [N/mm^2]
fctd=fctk/1.5 [N/mm^2]= 1.49 [N/mm^2]
PRIME ANALISI DELL’EDIFICIO
PRIME ANALISI DELL’EDIFICIO
fctk_0.05 = 0,7×fctm =
PRIME ANALISI DELL’EDIFICIO
PRIME ANALISI DELL’EDIFICIO
CARATTERISTICHE DELL’ACCIAIO
• Rapporto tra resistenza e tensione di snervamento (valore medio del rapporto):
ft/fy > 1,05
• Rapporto medio tra valore effettivo e valore nominale della resistenza a
snervamento:
fy,eff/fy,nom < 1,25
PRIME ANALISI DELL’EDIFICIO
Acciaio B450C:
fyd=450/1.15 [N/mm^2]= 391 [N/mm^2]
fyk= elasto plastico-indefinito
Modulo elastico Es=206000 MPa
Deformazione al limite elastico:
yd=fyd/ Es=391/206000=1,89
PRIME ANALISI DELL’EDIFICIO
PRIME ANALISI DELL’EDIFICIO
PER LA REALIZZAZIONE DELLA STRUTTURA SI CONSIDERANO I
MATERIALI RIPORTATI NEL SEGUITO CON LE CARATTERISTICHE
NECESSARIE PER L’ANALISI DEI CARICHI:
Tompagni
Fodera interna (laterizi forati)
8 kN/m3
Fodera esterna (laterizi forati)
8 kN/m3
PAVIMENTI ED INTONACI
Intonaco interno
18 kN/m3
PAVIMENTO IN MARMO
27 kN/m3
Intonaco interno ed esterno
18 kN/m3
PRIME ANALISI DELL’EDIFICIO
Analisi dei carichi verticali per il dimensionamento
Tompagni esterni
Fodera interna (10 cm)
0,8 kN/m2
Fodera esterna (15 cm)
1,2 kN/m2
Intonaco interno (2 cm)
0,36 kN/m2
Intonaco esterno (2 cm)
0,36 kN/m2
carichi strutturali portati
Incidenza Tramezzi
Gk2’=2,72 kN/m2
1,20 kN/m2
Si considera un 25% in meno per la presenza dei vuoti (porte e
finestre)=0,75*2,72=2,04[KN/m2]
Carichi Accidentali
Sono forniti dalle NTC-2008 nella misura di 3,00 kN/m2 (cat C1-Ospedale) per
ambienti suscettibili di affollamento e di 0,50 kN/m2 per coperture non accessibili
PRIME ANALISI DELL’EDIFICIO
Dimensione
Solai di interpiano
SIMBOLO
soletta
altezza pignatta
larghezza pignatta
base travetto
altezza totale solaio
massetto in
calcestruzzo leggero
pavimento
(cm)
s
hp
bp
b
H
Campata
5
16
38
12
21
sbalzo
5
16
38
12
21
sm
6
6
sp
3
2
sc
smb
p
s
hp
si
bp
i
b
sm
H
PRIME ANALISI DELL’EDIFICIO
Solai di interpiano
PESO PROPRIO SOLAIO
Elemento/i
Simbolo
formula
Peso
Valori numerici
(kN/m2)
1.25
soletta
G1s
s x larghezza x profondità x ps
travetti
G1t
[base x altezza x profondità x ps] x ntrav. al m 0.12 x 0.16 x 1 x 25 x 2
0.96
[base x altezza x profondità x ps] x nfile
0.38 x 0.16 x 1 x 8 x 2
0,97
G1s + G1t + G1l
1.25 + 0.96 + 0.97
3.18
pignatte
G1l
PESO PROPRIO
SOLAIO G1
0.05 x 1 x 1 x 25
CARICHI PERMANENTI NON STRUTTURALI
Elemento/i
Simbolo
pavimento
massetto
intonaco
Incidenza
tramezzi
G2p
G2m
G2i
G2t
G2
formula
sp x larghezza x profondità x ps
sm x larghezza x profondità x ps
si x larghezza x profondità x ps
Valori numerici
0.03 x 1 x 1 x 27
0.06 x 1 x 1 x 14
0.015 x 1 x 1 x 20
Peso
(kN/m2)
0.8
0.84
0.3
1,2
G2p + G2m + G2i+ G2t
0.8+0.84+0.3+1.2
3.14
PRIME ANALISI DELL’EDIFICIO
Solai di balconi
PESO PROPRIO SOLAIO
Elemento/i Simbolo
formula
Valori numerici
(kN/m2)
soletta
G1s
s x larghezza x profondità x ps
travetti
G1t
[base x altezza x profondità x ps] x ntrav. al m 0.12 x 0.16 x 1 x 25 x 2
0.96
pignatte
G1l
[base x altezza x profondità x ps] x nfile
0.38 x 0.16 x 1 x 8 x 2
0,97
G1s + G1t + G1l
1.25 + 0.96 + 0.97
3.18
PESO PROPRIO
SOLAIO G1
0.05 x 1 x 1 x 25
Peso
1.25
PRIME ANALISI DELL’EDIFICIO
RIEPILOGO DEI CARICHI DA ASSEGNARE:
Carichi strutturali (auto-portati dal solaio)
Gk1
3,18
[kN/m2]
Carichi non strutturali permanenti
Gk2
3,14
[kN/m2]
Tompagni esterni
Gk2’
2,04
[kN/m2]
Carichi accidentali (cat. C1 Ospedale)
Qk1
3,00
[kN/m2]
Carichi accidentali copertura
Qk2
0,50
[kN/m2]
2° carichi NON strutturali permanenti - tompa. est
Gk2”=2,04 [KN/m]
PRIME ANALISI DELL’EDIFICIO
Predimensionamento TRAVI
Per quanto concerne le travi, per semplicità, vengono predimensionate per soli carichi verticali.
Relativamente allo schema statico, si può fare riferimento o ad una trave continua su più appoggi, oppure,
ad un’unica trave appoggiata-appoggiata o appoggiata-incastrata o incastrata-incastrata (con momento
massimo in mezzeria pari a ql2/8; ql2/14; ql2/24).
La misura cautelativa è adottata, per tenere presente che, in questa fase, non vengono portate in
conto le azioni orizzontali (forze sismiche).
Posta la distinzione tra travi a spessore di solaio con altezza pari allo spessore del solaio e travi emergenti
con altezze maggiori dello spessore del solaio si sceglie di prendere delle travi emergenti sul contorno
della struttura e delle travi a spessore per le travi interne. I limiti sulle altezze per entrambe le tipologie di
travi sono:
H 1/20 –1/25 lmax per le travi a spessore
H 1/10 –1/14 lmax per le travi emergenti
Per le travi a spessore in particolare una regola grossolana di predimensionamento permette di
dimensionarne la base come:
B=lmax/6
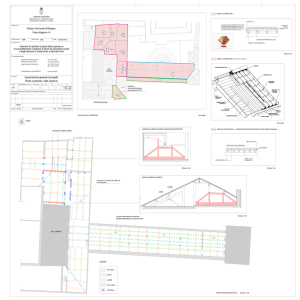
PROGETTO E VERIFICA PER AZIONI SISMICHE DI UN EDIFICIO IN C.A. CON SAP 2000
PROGETTO E VERIFICA PER AZIONI SISMICHE DI UN EDIFICIO
IN C.A. CON SAP 2000
LE IPOTESI DI CALCOLO:
PIANTA 1°,2° E 3 ° IMPALCATO
PIANTA 4° E 5 ° IMPALCATO
84
PROGETTO E VERIFICA PER AZIONI SISMICHE DI UN EDIFICIO
IN C.A. CON SAP 2000
Predimensionamento TRAVI
Il predimensionamento è ora possibile poiché sono noti i carichi da assegnare alle varie travi:
TRAVI DI BORDO
TRAVI PORTANTI
TRAVI NON PORTANTI
PROGETTO E VERIFICA PER AZIONI SISMICHE DI UN EDIFICIO
IN C.A. CON SAP 2000
Predimensionamento TRAVI
Per le travi scalate :
Gk1= peso trave(Pt )+inc. solaio=0.3*0.6*25+3.18*(4,00)
= 17,22 [kN / m]
Gk2’= inc. solaio portato
= 12.56 [kN / m]
=3.14*(4,00)
Gk2’’= incid. Tamponamenti =2,04*(3,50)
=
7,14 [KN/m]
Qk = 3,00*(4,00)
= 12 kN / m
Fd = g1*Gk1+ g2*Gk12 +q*Qk= 1,3*17.22+1,5*12.56+1,5*12+1,5*7,14 = 69,94 kN/m
Fd  l 2 69.94  62
Md 

 209.82kNm
12
12
PROGETTO E VERIFICA PER AZIONI SISMICHE DI UN EDIFICIO
IN C.A. CON SAP 2000
Predimensionamento TRAVI EMERGENTI
L’altezza della sezione della trave viene determinata andando ad imporre che il momento flettente sia
equilibrato dalla coppia interna data dal prodotto della risultante di compressione e di trazione per il braccio d*.
In modo approssimato con il metodo dello stress block:
ecm
H
y
xc
A’f
C
M
cy
Af
T
b
ey
(a)
(b)
Mrd  T  d *  As  f sd  0.9  d
d*=57 [cm]=altezza utile sezione
Si ottiene un’armatura As=10,46 [cm^2]= 5 f 18
d*
PROGETTO E VERIFICA PER AZIONI SISMICHE DI UN EDIFICIO
IN C.A. CON SAP 2000
Predimensionamento TRAVI A SPESSORE
Per trave a spessore, con spessore del solaio pari a 20 [cm]:
Si ottiene un’armatura As=35,07 [cm^2]=14 f 18
Per il solaio dovremmo cambiare sezione poiché lo spessore di 20 cm diviene esiguo per
la luce di 6 m! Aumenterebbe pertanto nell’analisi dei carichi il valore del peso proprio
IN QUESTO CALCOLO SI E’ TRASCURATA LA DIFFERENZA DI CARICO DOVUTA ALLA
DIFFERENZA PESO TRA LA TRAVE A SPESSORE E QUELLA EMERGENTE. Inoltre le travi di bordo
che portano meno carico per ora non sono state differenziate .
PROGETTO E VERIFICA PER AZIONI SISMICHE DI UN EDIFICIO
IN C.A. CON SAP 2000
Predimensionamento TRAVI
E SE AVESSIMO SCELTO L’ORDITURA DEL SOLAIO O IN MODO PERPENDICOLARE ALLE
TRAVI DI LUCE MINORE?
PROGETTO E VERIFICA PER AZIONI SISMICHE DI UN EDIFICIO
IN C.A. CON SAP 2000
Predimensionamento TRAVI EMERGENTI
Per le travi scalate :
Gk1/m= peso trave(Pt )+inc. solaio=0.3*0.6*25+3.18*(6,00) = 23,58 kN / m
Gk2/m= inc. solaio portato
=3.14*(6,00)
= 18.84 kN / m
Gk2/m= inc. tompagni =2,04*(3,50)
= 7,14 [KN/m]
Qk /m= 3,00*(6,00)
= 18 kN / m
d*=57 [cm]=altezza utile sezione
Fd = g1*Gk1+ g2*Gk12 +q*Qk= 1,3*23.58+1,5*18.84+1,5*18+1.5*7,14 = 90,85 kN / m
Fd  l 2 90.85  42
Md 

 121.13kNm
12
12
Si ottiene un’armatura As=6,04 [cm^2] = 3 f 18
Per trave a spessore, con spessore del solaio pari a 35 [cm]:
Si ottiene un’armatura As=10,75 [cm^2] = 5 f 18
Dovremmo cambiare
sezione di solaio
comunque!
PROGETTO E VERIFICA PER AZIONI SISMICHE DI UN EDIFICIO
IN C.A. CON SAP 2000
I pilastri, in prima analisi, possono essere predimensionati a sforzo normale in funzione di tutti
i carichi verticali che gravano su di essi, assegnando delle dimensioni iniziali che potranno
essere corrette di volta in volta nell’inserimento dei parametri.
Individuando per ogni pilastro “ i ”, ad ogni piano “ j ”, la sua area di influenza Aij se ne
calcola il peso tenendo presente sia il contributo dei carichi permanenti che quello relativo ai
carichi variabili. La sezione del pilastro“ i ” al piano “ j ” sarà così dimensionata in base al
carico complessivo Nd relativo al piano j-mo e a tutti i piani superiori allo stesso
sforzo normale al
generico piano j-mo
N dj  N j  N gj
Carichi permanenti e
accidentali
Peso proprio
PROGETTO E VERIFICA PER AZIONI SISMICHE DI UN EDIFICIO
IN C.A. CON SAP 2000
1° osservazione : i pilastri di un edificio sono sollecitati a pressoflessione i cui valori derivano dalla risoluzione completa
dello schema strutturale e pertanto non noti in questa fase.
2° osservazione : I domini di resistenza a pressoflessione variano poco con la larghezza della sezione mentre dipendono
fortemente dall’altezza.
Hanno forma pressoché parabolica con i valori massimi del momento in corrispondenza di
circa il 50% di Nd.
M
0,5 Nd
N
3° osservazione : La duttilità di una sezione diminuisce fortemente all’aumentare della sollecitazione di compressione
media.
PROGETTO E VERIFICA PER AZIONI SISMICHE DI UN EDIFICIO
IN C.A. CON SAP 2000
4° osservazione : Si consiglia pertanto di predimensionare i pilastri con un valore massimo della sollecitazione di
compressione pari al 30-40% di quella di calcolo.
fcd_p=0,3 fcd =0,3* 19,83= 5,9 [N/mm2]
5° osservazione : Se la carpenteria è sufficientemente regolare anche le sezioni saranno poco diverse tra loro. Inoltre
mentre nel caso di edifici con numero di piani elevato (>7-8) è buona norma ridurre la dimensione
della sezione del pilastro ai piano più alti per via delle minori tensioni dovute a minore sollecitazioni
sismica, per edifici più bassi, se l’architettonico lo consente, si può adottare una sezione costante.
6° osservazione : Per il predimensionamento del pilastro sono necessari i valori di massima dello SFORZO
NORMALE e del MOMENTO FLETTENTE. In realtà per il calcolo di quest’ultimo è
necessario ricavare anche il valore del TAGLIO. In particolare i valori di N derivano dai carichi
verticali e dall’incremento di N dovuto all’azione sismica. I valori di M sono in pratica
quelli provenienti dall’azione sismica, essendo quelli dovuti ai carichi verticali molto
contenuti se rapportati ai momenti flettenti del sisma.
7° osservazione: i pilastri devono essere sovradimensionati e non si devono avere travi eccessivamente
resistenti, per rispettare la gerarchia delle resistenze per lo SLU e anche per il rispetto
della verifica di deformabilità dello SLD. Per ragioni di regolarità in elevazione e per
motivi pratici si consiglia, per ciascun pilastro, al massimo una rastremazione della
sezione trasversale di 10 cm per piano.
PROGETTO E VERIFICA PER AZIONI SISMICHE DI UN EDIFICIO
IN C.A. CON SAP 2000
Predimensionamento pilastri – Calcolo massima dello sforzo normale
Nj5
Nj5
Nj4
Ngi
Nj4
Considereremo per il peso proprio del pilastro una sezione 50 x 50
[cm] (NCT 2008: dimensione minima 250mm)
Ngj    A pj  h  s
Dove s è il coefficiente di continuità che è pari:
Nj3
Ngi
Nj2
Ngi
Nj1
Ngi
Nj3
Pilastri interni => s= 1,2 1,3
Pilastri esterni => s= 1,1
Pilastri esterni di spigolo => s= 1
Nj2
Utilizzando le aree di influenza per la valutazione dei carichi che competono ad ogni singolo
pilastro non si tiene conto dalla continuità delle travi nelle due direzioni. Detto effetto potrebbe
essere considerato utilizzando dei coefficienti di continuità in entrambe le direzioni, per i pilastri
interni, o una di esse per i pilastri laterali che amplificano i carichi
Nj1
Peso del pilastro di dimensioni minime al piano generico:
Ngpil11    A p11  h  s  2500 * 0,50 * 0,50  3,5 *1,3  2843daN
PROGETTO E VERIFICA PER AZIONI SISMICHE DI UN EDIFICIO
IN C.A. CON SAP 2000
Predimensionamento pilastri – calcolo di massima sforzo normale
Resistenza di calcolo per sforzo normale centrato
a=4m
L’area di influenza di ogni pilastro si considera per
semplicità pari a Aij =4 x 6 = 24 [m^2]
b=6m


e
  1.5  G impalcato
N j  1.3  G impalcato
 Aij  G ktravi  (a  b)  G pilastri
 A ij  G ktamponatur
 a   1.5  Q k  A ij  s 
k1
k
k2
2
 1.3  3,18  24  0,3  0,6  25  (6  4)  25  0,5  0,5  3,5  1.5  3,14  24  7,14  4  1.5  3  24 1,3  846,52kN
N j  846,52 [kN]
A
846520
 1434777,97 mm 2  B  H 
5.9
Si scegli di dimensionare
tutti i pilastri 40x40
f cd  5.9 [MPa]
138657.63  379mm  40 x 40cm
Att.: Solo carichi
verticali
PROGETTO E VERIFICA PER AZIONI SISMICHE DI UN EDIFICIO
IN C.A. CON SAP 2000
Controllo di regolarità
PROGETTO E VERIFICA PER AZIONI SISMICHE DI UN EDIFICIO
IN C.A. CON SAP 2000
Controllo di regolarità
PROGETTO E VERIFICA PER AZIONI SISMICHE DI UN EDIFICIO
IN C.A. CON SAP 2000
Controllo di regolarità – calcolo delle masse sismiche
Calcolo dei pesi simici a ciascun impalcato
PROGETTO E VERIFICA PER AZIONI SISMICHE DI UN EDIFICIO
IN C.A. CON SAP 2000
Controllo di regolarità – calcolo delle masse sismiche
Calcolo delle masse sismiche
Le masse simiche si calcolano dai pesi simici dividendoli per l’accelerazione di
gravità g=9,81m/s2
La massa rotazionale si calcola moltiplicando la massa M per il quadrato del raggio
di inerzia r
Baricentro delle masse
PROGETTO E VERIFICA PER AZIONI SISMICHE DI UN EDIFICIO
IN C.A. CON SAP 2000
Controllo di regolarità – esempio di controllo della variazione delle masse
PROGETTO E VERIFICA PER AZIONI SISMICHE DI UN EDIFICIO
IN C.A. CON SAP 2000
Controllo di regolarità –controllo della variazione delle rigidezze
Per effettuare la verifica di regolarità in termini di rigidezze, bisogna prima modellare la
struttura ed applicare in ciascuna delle due direzioni, separatamente, le azioni sismiche;
dunque si calcola la rigidezza come rapporto tra il taglio complessivo agente al piano
(«taglio di piano») e lo spostamento relativo al piano d, conseguente a tali azioni
Il taglio di piano è la sommatoria delle azioni orizzontali agenti al di sopra del piano
considerato
La forza da applicare ad ogni piano si ottiene dall’analisi statica lineare
PROGETTO E VERIFICA PER AZIONI SISMICHE DI UN EDIFICIO
IN C.A. CON SAP 2000
Controllo di regolarità –controllo della variazione delle rigidezze – analisi statica lineare per la valutazione delle rigidezze
PROGETTO E VERIFICA PER AZIONI SISMICHE DI UN EDIFICIO
IN C.A. CON SAP 2000
Controllo di regolarità –controllo della variazione delle rigidezze – analisi statica lineare per la valutazione delle rigidezze
PROGETTO E VERIFICA PER AZIONI SISMICHE DI UN EDIFICIO
IN C.A. CON SAP 2000
Incremento dello sforzo normale agente sui pilastri
Analisi statica equivalente ci permette
anche di stimare più accuratamente la
sollecitazione nei pilastri
L’entità delle azioni sismiche è rilevante in rapporto ai carichi verticali. Di conseguenza lo sforzo normale sui pilastri potrebbe
variare molto nei pilastri di estremità; per i pilastri interni la variazione di sforzo assiale è invece dovuta alla differenza di
tagli indotti dal sisma nelle travi ed è quindi in genere trascurabile a meno che non vi sia una forte differenza di luce o di
sezione tra due travi che convergono nel pilastro.
La variazione di sforzo normale indotta dal sisma può essere valutata con un modello locale
come somma dei tagli nelle travi ai diversi piani o con un modello globale (in caso di edificio a
pianta rettangolare) che usa il momento ribaltante alla base dell’edificio.
PROGETTO E VERIFICA PER AZIONI SISMICHE DI UN EDIFICIO
IN C.A. CON SAP 2000
Incremento dello sforzo normale agente sui pilastri
A5
40x40
A4
40x40
A3
A2
A1
50x50
60x50
60x50
Rifare di controlli di
regolarità!