taratura statica

Argomenti del corso
Parte I – Caratteristiche generali e strumenti terminali
3.
Prestazioni generali degli strumenti di misura:
caratteristiche statiche
• Taratura statica
• Elaborazione statistica dei dati – Cenni
• Metodo dei minimi quadrati
• Analisi e determinazione dell’incertezza di
misura, normativa di riferimento, propagazione
delle incertezze
• Sensibilità statica, Linearità, Risoluzione,
Ripetibilità, Soglia, Isteresi, Precisione, Campo di
misura
• Effetti di inserzione: impedenza e ammettenza
generalizzate di uno strumento
Misure Meccaniche e Termiche – Anno accademico 2014/15
Taratura statica
Importanza e finalità
•
La qualità di una misura (come capacità di descrivere la realtà fisica nel modo più
fedele e accurato possibile) dipende dalle decisioni assunte nell’ambito del
metodo di misura ed in particolare dalla scelta dello strumento
•
La scelta è fatta in base alle caratteristiche metrologiche dello strumento =
prestazioni nei confronti degli ingressi ai quali lo strumento è sensibile
•
La taratura statica è l’operazione relativa alla determinazione delle
caratteristiche metrologiche di uno strumento nel caso di ingressi costanti
(statici)
Misure Meccaniche e Termiche – Anno accademico 2014/15
Taratura statica
Importanza e finalità
•
La taratura statica è un procedimento atto a determinare “come i segnali di
uscita sono legati alle misure dei misurandi” (UNI 4546) e quindi quali
relazioni intercorrono fra essi e con quale incertezza vengono stimati i misurandi
•
La taratura:
- è un’operazione eseguita da chi progetta e costruisce uno strumento;
- fornisce dati utili a chi deve scegliere ed utilizzare uno strumento;
- è un’operazione eseguita periodicamente per verificare che le caratteristiche
rimangano inalterate nel tempo;
- è un’operazione eseguita prima di ogni misura nel caso di strumenti e/o situazioni
particolari che lo richiedono
Misure Meccaniche e Termiche – Anno accademico 2014/15
Taratura statica
Metodo di taratura
•
Tutti gli ingressi eccetto uno sono fissati a valori costanti
•
L’ingresso d’interesse è fatto variare in un intervallo di valori costanti
•
Taratura: relazione tra i valori d’ingresso e di uscita per i valori costanti degli altri
ingressi
•
Descrive una situazione ideale (nella realtà non è possibili controllare tutti gli altri
ingressi e mantenerli costanti)
Misure Meccaniche e Termiche – Anno accademico 2014/15
Taratura statica
Processo di taratura
Realizzazione pratica del metodo di taratura
•
Analisi del principio di funzionamento, del metodo di misura e dell’ambiente di
utilizzo dello strumento
 elenco dei possibili ingressi ai quali lo strumento è sensibile
 definizione di un modello teorico dello strumento
•
Scelta degli ingressi da tenere sotto controllo nella taratura, da misurare con
mezzi indipendenti di accuratezza adeguata
Esempio: variazione di 100°C provoca un errore sulla misura di pressione con un
manometro di 0.100%, se il termometro misura con un errore del 2%, l’errore
sulla determinazione della pressione è 0.102%: l’accuratezza è più elevata del
necessario.
Misure Meccaniche e Termiche – Anno accademico 2014/15
Taratura statica
Processo di taratura
•
Scelta dello strumento campione: strumento che permette la determinazione
dell’ingresso desiderato con un’incertezza 10 volte inferiore
Strumento campione:
Strumento di cui sia nota l’incertezza tramite la sua proprietà di riferibilità, acquisita
se lo strumento è stato calibrato “impiegando misurandi le cui misure sono state
assegnate con riferimento a campioni riconosciuti come primari” (UNI 4546)
La riferibilità presuppone che sia stata stabilita una gerarchia di campioni e strumenti
con incertezza crescente
Nella gerarchia i campioni più accurati sono detti campioni primari
Misure Meccaniche e Termiche – Anno accademico 2014/15
Taratura statica
Processo di taratura
Strumento campione:
I campioni primari sono realizzati e mantenuti in laboratori nazionali:
negli US: NIST (National Institute for Standards and Technology)
In Italia: I.N.RI.M. (Istituto Nazionale di Ricerca Metrologica)
afferente al Ministero dell’Università e della Ricerca e nato
dalla fusione di IMGC (Istituto Metrologico “G. Colonnetti”)
e IEN (Istituto Elettrotecnico Nazionale “G. Ferraris”) ed ENEA
Misure Meccaniche e Termiche – Anno accademico 2014/15
Taratura statica
Processo di taratura
Campioni primari
I campioni nazionali realizzano le unità SI e sono riportati nel Decreto Ministeriale
n. 591 e costituiscono il riferimento metrologico dei Centri di Taratura
Il riferimento metrologico italiano può anche essere realizzato tramite la
disseminazione delle unità SI fatta dagli Istituti metrologici firmatari dell’accordo
redatto dal Comitato Internazionale dei Pesi e Misure (CIPM – MRA), oppure
dell’accordo multilaterale (EA – MLA) della Cooperazione Europea per
l’Accreditamento (EA – European cooperation for Accreditation)
Misure Meccaniche e Termiche – Anno accademico 2014/15
Taratura statica
Campioni primari
Da: Decreto Ministeriale 30 Nov 1993, n. 591, “Regolamento concernente la
determinazione dei campioni nazionali di talune unità di misura del SI in attuazione
dell’art. 3 della legge 11 agosto 1991, n. 273”
Campioni di unità SI di base
Lunghezza
IMGC
Massa
IMGC
Tempo
IEN
Intensità di corrente el.
IEN
Temperatura termodinamica IMGC
Intensità luminosa
IEN
Misure Meccaniche e Termiche – Anno accademico 2014/15
Taratura statica - Campioni
Campioni di unità SI derivate
Angolo piano
IMGC
Massa volumica
IMGC
Portata di massa
IMGC
Forza
IMGC
Pressione
IMGC
Pressione sonora
IEN
Potenza elettrica
IEN
Tensione elettrica
IEN
Intensità di campo elettrico
IEN
Resistenza elettrica
IEN
Misure Meccaniche e Termiche – Anno accademico 2014/15
Campioni di unità SI derivate
Capacità elettrica
IEN
Flusso di induzione magn.
IEN
Induzione magnetica
IEN
Induttanza
IEN
Flusso luminoso
IEN
Attività (dei radionuclidi)
ENEA
Dose assorbita
ENEA
Densità di flusso di neutroni
ENEA
Esposizione
ENEA
Campioni di unità non SI
Scale di durezza
IMGC
Misure Meccaniche e Termiche – Anno accademico 2014/15
Taratura statica
SIT - Servizio di taratura in Italia
•
Dal 1979 gli Istituti metrologici primari IMGC/CNR, IEN e INRIM/ENEA hanno
accreditato numerosi laboratori metrologici secondari come Centri di Taratura
costituendo il SIT – Servizio Italiano di Taratura
•
Dal 2003 responsabilità e controllo di accreditamento sono della Segreteria
Centrale del SIT. Dal 2004 tale autorità è estesa a ogni tipo di Laboratorio di
taratura, per qualunque tipo di grandezza fisica
•
Per accreditare un laboratorio quale Centro di Taratura, il SIT si avvale di esperti
degli Istituti primari come ispettori tecnici, applica procedure di mantenimento,
estensione o riduzione, rinnovo, sospensione o revoca dell’accreditamento
Misure Meccaniche e Termiche – Anno accademico 2014/15
Taratura statica
SIT - Servizio di taratura in Italia
•
La procedura di accreditamento iniziale si conclude con l’emissione di un
Certificato di accreditamento in cui si attesta la competenza del Laboratorio a
eseguire tarature che assicurano nel tempo la riferibilità ai campioni e riconosce
al Laboratorio la facoltà di emettere certificati di taratura SIT per gli strumenti, i
campi, le incertezze e le condizioni di misura specificate
•
La riferibilità della strumentazione è richiesta in misura crescente nei più diversi
settori: ricerca&sviluppo, laboratori di prova per la certificazione di prodotti,
sistemi per il controllo automatico di processi di produzione, PA
Misure Meccaniche e Termiche – Anno accademico 2014/15
Taratura statica
Misure Meccaniche e Termiche – Anno accademico 2014/15
Taratura statica
SNT – Sistema Nazionale di Taratura
•
Istituito con la legge 11 agosto 1991 n. 273 “Il sistema nazionale di taratura è
costituito dagli istituti metrologici primari e dai centri di taratura e ha il compito di
assicurare la riferibilità ai campioni nazionali dei risultati delle misurazioni”
•
“Gli Istituti metrologici primari effettuano studi e ricerche finalizzati alla
realizzazione dei campioni primari delle unità di misura di base, supplementari e
derivate del SI” e ne “assicurano la conservazione nel tempo”.
•
“Inoltre procedono alla disseminazione delle unità di misura con essi realizzate,
attuando tutte le operazioni tecniche e procedurali che consentono e
garantiscono il trasferimento delle unità di misura dal livello di riferimento dei
campioni primari a quello applicativo attraverso una catena ininterrotta di
confronti”
Misure Meccaniche e Termiche – Anno accademico 2014/15
Taratura statica
SNT – Sistema Nazionale di Taratura
•
MIUR e MAP svolgono funzioni di indirizzo e coordinamento del SNT
•
“I centri di taratura sono costituiti da laboratori di idonea valenza tecnica e
organizzativa convenzionati con gli istituti metrologici primari per l’effettuazione
della taratura degli strumenti di misura sulla base di campioni secondari
confrontati periodicamente con i campioni nazionali” (MIUR e MAP pubblicano
ogni anno sulla Gazzetta Ufficiale l’elenco dei Centri SIT)
•
“Il Comitato centrale metrico definisce le procedure per la campionatura delle
misure di uso regionale, di concerto con il competente assessore regionale”,
svolge anche funzioni di consulenza e di proposta nell’ambito del SNT
Misure Meccaniche e Termiche – Anno accademico 2014/15
Taratura statica
Processo di taratura
•
Predisposizione di un banco che consenta di variare gli ingressi uno alla volta e
tenere sotto controllo gli altri
•
Variazione degli ingressi in un determinato intervallo e registrazione delle
relazioni ingresso-uscita
Misure Meccaniche e Termiche – Anno accademico 2014/15
Taratura statica
Valore misurato e valore vero
•
Il valore vero di una grandezza fisica non è conoscibile, si parla di valore di
riferimento ottenuto da una misurazione eseguita con un metodo esemplare
•
Il metodo esemplare è sufficientemente accurato per lo scopo finale della
misurazione
•
Il processo di taratura, come ogni altro processo di misura, è la realizzazione
pratica di questo metodo
•
Ogni processo di taratura se ripetuto diverse volte, genera una sequenza casuale
di dati, cioè letture diverse pur mantenendo inalterate le condizioni di misura
Misure Meccaniche e Termiche – Anno accademico 2014/15
Taratura statica
Controllo statistico
•
Ogni strumento ha un numero infinito di ingressi (ad esempio: temperatura,
pressione, umidità)
•
Nella procedura di taratura si specifica che certi ingressi, in grado di dare i
contributi più importanti all’incertezza di misura, sono mantenuti costanti entro
determinati limiti – gli altri sono lasciati incontrollati
•
Se il processo di misurazione è in stato di controllo statistico, ripetendo la misura
n volte si ottiene una serie di dati con dispersione di tipo casuale – la sequenza
casuale si può usare per descrivere il processo di misura e stimare l’incertezza
•
E’ importante quindi considerare la deviazione dalle condizioni di taratura delle
effettive condizioni di utilizzo di uno strumento
Misure Meccaniche e Termiche – Anno accademico 2014/15
Taratura statica
Processo di taratura
Esempio: manometro
Ingressi significativi:
-
Temperatura (espansioni o contrazioni)
Accelerazione (indicazione errata)
Vibrazione (indicazione errata)
Misure Meccaniche e Termiche – Anno accademico 2014/15
Elaborazione statistica dei dati - Cenni
Misure ripetute
Esempio: manometro
-
Campione di riferimento
Ingressi controllati
dispersione casuale
Cause:
Sistema di misura: risoluzione, ripetibilità
Procedimento: ripetibilità
Variabile misurata: variazioni spaziali e
temporali
Misure Meccaniche e Termiche – Anno accademico 2014/15
Elaborazione statistica dei dati - Cenni
Istogramma
Esempio: manometro
- Ordine letture e suddivisione in
intervalli di uguale ampiezza
- Si definisce Z come:
Z
(numero di letture in un intervallo)/(numero totale di letture)
ampiezza dell' intervallo
Con un numero di intervalli K pari a:
K= 1.87 (N-1)0.40+1
Istogramma
Misure Meccaniche e Termiche – Anno accademico 2014/15
Elaborazione statistica dei dati - Cenni
Funzione densità di probabilità
- Numero ipoteticamente infinito di letture
- Istogramma
Curva continua
Funzione densità di probabilità
Z = f(x)
b
p(a  x  b)   f ( x)dx
probabilità che una lettura sia compresa fra a e b
a
x
F ( x) 
 f ( x)dx

probabilità che la lettura sia minore di un certo valore di x
(funzione di distribuzione cumulata)
Misure Meccaniche e Termiche – Anno accademico 2014/15
Elaborazione statistica dei dati - Cenni
Distribuzione gaussiana
- La funzione di densità di probabilità più
utilizzata e utile è la funzione normale,
Gaussiana
f ( x) 
2
2
1
e ( x   ) /( 2 )
2
-   x  
68% µ ± 1
95% µ ± 2
99.7% µ ± 3
Nella realtà le distribuzioni sono limitate a valori finiti
Misure Meccaniche e Termiche – Anno accademico 2014/15
Elaborazione statistica dei dati - Cenni
Distribuzione gaussiana
Deviazione standard (popolazione infinita):
n

 x   
i
i 1
n
Per N punti campione (popolazione finita):
Media campionaria
Deviazione standard del
campione
N
x
x
i 1
N
N
i
sx 
Deviazione standard
della media
 x  x 
i 1
2
i
N 1
Misure Meccaniche e Termiche – Anno accademico 2014/15
sx 
sx
M
Elaborazione statistica dei dati - Cenni
Valutazione di una gaussiana
- Distorsione asse verticale: si ottiene una
retta
- Carte di probabilità: l’asse delle ordinate
rappresenta la distribuzione cumulata
- Solo aumentando significativamente il
numero di campioni (aventi stessa media
campionaria e deviazione standard del
campione) la curva si approssima alla
retta (Gaussiana perfetta)
Misure Meccaniche e Termiche – Anno accademico 2014/15
Metodo dei minimi quadrati
Curva di taratura – Regressione lineare
Criterio di interpolazione più usato: retta dei
minimi quadrati
Linea che minimizza la somma dei
quadrati delle differenze, in direzione
verticale, tra i punti e la linea interpolante
qo  mqi  b
qo = lettura
qi = ingresso
m = coefficiente angolare
b = intercetta
Misure Meccaniche e Termiche – Anno accademico 2014/15
Metodo dei minimi quadrati
Retta interpolante
m
•
Parametri della retta dei minimi quadrati:
(qo )(qi2 )  (qi qo )(qi )
b
Nqi2  (qi ) 2
s 
2
m
•
Deviazioni standard:
Nqi qo  (qi )(qo )
Nqi2  (qi ) 2
s 
2
b
2
sqo

2
Nsqo
Nqi2  (qi ) 2
2
sqo
qi2
Nqi2  (qi ) 2
1
mqi  b  qo 

N 2
Misure Meccaniche e Termiche – Anno accademico 2014/15
Metodo dei minimi quadrati
Errori sistematici e casuali
2
sqo

1
mqi  b  qo 

N 2
Assumendo sqo uguale per ogni valore di qi,
si può calcolare sqo usando tutti i dati di
misura e senza ripetere la misura diverse
volte per lo stesso valore dell’ingresso
qi 
qo  0.847
1.082
2
2
s
q

b
1


qo
sqi2 
 qi   2
 o
N 2 m
m

Esempio: qo=4.32 kPa, la stima di qi è 4.78±0.58 kPa (±3s), e. sistematico: -0.46 kPa
Taratura: processo di eliminazione del bias e di definizione quantitativa dell’imprecisione
Misure Meccaniche e Termiche – Anno accademico 2014/15
Incertezza di misura
Analisi e determinazione dell’incertezza
Da UNI CEI ENV 13005:
“allorquando tutte le componenti di errore note o ipotizzate siano state valutate e le
relative correzioni apportate, rimane tuttavia un’incertezza sulla correttezza del
risultato, vale a dire un dubbio su quanto bene rappresenti il valore della quantità
misurata”
Analisi: valutazione delle possibili cause di incertezza
Determinazione: definizione quantitativa dei limiti di incertezza
Misure Meccaniche e Termiche – Anno accademico 2014/15
Incertezza di misura
La Norma UNI CEI ENV 13005
“Guida all’espressione dell’incertezza di misura”
Traduzione italiana della norma internazionale ISO ENV 13005 “Guide to the
expression of uncertainty in measurement” (GUM)
Definizione di incertezza: “parametro, associato al risultato di una misurazione, che
caratterizza la dispersione dei valori ragionevolmente attribuibili al misurando”
Distinzione di incertezza in base ai metodi usati per valutarla:
• Tipo A: si basa su analisi statistica e osservazioni sperimentali
• Tipo B: si basa sull’utilizzo di dati esterni quali misure precedenti, certificati di
taratura, specifiche di costruttori, manuali
In entrambi i casi: distribuzioni di probabilità, quantificazione tramite varianze e scarti
tipo
Misure Meccaniche e Termiche – Anno accademico 2014/15
Incertezza di misura
Valutazione dell’incertezza tipo - UNI CEI ENV 13005
Valutazione di categoria A
Approccio: misure ripetute, in condizioni controllate
Da N osservazioni statisticamente indipendenti, la miglior stima di una grandezza X è
la media sperimentale del campione:
1
x
N
N
x
j 1
j
La variabilità delle misure si può esprimere tramite la varianza campionaria che
rappresenta una stima della varianza della variabile aleatoria X:
1 N
2


s 
x

x
 j
N  1 j 1
2
x
Misure Meccaniche e Termiche – Anno accademico 2014/15
Incertezza di misura
Valutazione dell’incertezza tipo - UNI CEI ENV 13005
Per la definizione di incertezza si utilizza la varianza sperimentale della media:
N
s x2
1
2


s  
x

x
 j
N N ( N  1) j 1
2
x
L’incertezza di misurazione si pone pari allo scarto tipo sperimentale della media:
u( x )  sx 
sx
N
Misure Meccaniche e Termiche – Anno accademico 2014/15
Incertezza di misura
Valutazione dell’incertezza tipo - UNI CEI ENV 13005
Valutazione di categoria B Approccio: giudizio scientifico su tutte le informazioni
utili sulla possibile variabilità di X
Informazioni utili:
•
•
•
•
•
dati da precedenti misurazioni;
esperienza o conoscenza del comportamento e delle proprietà dei materiali e
strumenti di interesse;
specifiche tecniche del costruttore;
dati forniti in certificati di taratura o rapporti simili;
incertezze assegnate a valori di riferimento presi da manuali
u ( x)     2 
2


x


p( x)dx
x

Misure Meccaniche e Termiche – Anno accademico 2014/15
Incertezza di misura
Valutazione dell’incertezza tipo - UNI CEI ENV 13005
Valutazione di categoria B
-
-
In certi casi viene indicato dal produttore il livello di fiducia: in tal caso si suppone
una distribuzione normale
Qualora si sappia che Xi ha uguale probabilità di giacere in un intervallo compreso
tra a- e a+ è sempre uguale a 1, si assume:
xi 
a  a 
2
a2
2
u xi  
3
p
2a
a
1
a  a 
2
distribuzione rettangolare
xi
Misure Meccaniche e Termiche – Anno accademico 2014/15
Incertezza di misura
Valutazione dell’incertezza tipo - UNI CEI ENV 13005
Valutazione di categoria B
-
Una distribuzione trapezoidale ha maggior significato fisico:
u xi   a
2
1   
2
2
6
0   1
p
2aβ
β=1 distribuzione rettangolare
β=0 distribuzione triangolare
xi
Misure Meccaniche e Termiche – Anno accademico 2014/15
Incertezza di misura
Valutazione dell’incertezza tipo - UNI CEI ENV 13005
Valutazione dell’incertezza tipo composta
Misurando determinato a partire da N grandezze Xi:
Y  f ( X 1 , X 2 ,..., X N )
Xi sono variabili aleatorie: Y è una variabile aleatoria la cui stima si ricava da:
y  f ( x1 , x2 ,..., xN )
L’incertezza associata a Y prende il nome di incertezza tipo composta e per calcolarla
si utilizza la legge di propagazione dell’incertezza, che considera le incertezze tipo
di tutte le grandezze di ingresso
Misure Meccaniche e Termiche – Anno accademico 2014/15
Incertezza di misura
Valutazione dell’incertezza tipo - UNI CEI ENV 13005
Propagazione dell’incertezza per grandezze non correlate
Incertezza tipo composta di Y:
2
N
 f  2
2
 u ( xi )   ci2u 2 ( xi )
uc ( y )   
i 1  xi 
i 1
N
2
 f  2
 u ( xi ) 
uc ( y )   
i 1  xi 
N
N
c u
i 1
2
i
2
( xi )
Le derivate parziali sono i coefficienti di sensibilità, che descrivono come varia la
stima d’uscita y al variare dei valori delle stime d’ingresso (sono “pesi” in senso
statistico)
Misure Meccaniche e Termiche – Anno accademico 2014/15
Incertezza di misura
Valutazione dell’incertezza tipo - UNI CEI ENV 13005
Propagazione dell’incertezza per grandezze correlate
Incertezza tipo composta di Y:
N
N 1 N
 f 
 f 
 f  f 
2
u ( xi , x j )





uc ( y )    
u xi , x j    
 2  




i 1 j 1  xi 
i 1  xi 
i 1 j i 1 xi  x j 
N
2
N
Il parametro u(xi, xj) è la covarianza di xi e xj.
La dipendenza tra variabili aleatorie è espressa tramite il coefficiente di correlazione:
r ( xi , x j ) 
u ( xi , x j )
u ( xi )u ( x j )
Misure Meccaniche e Termiche – Anno accademico 2014/15
Incertezza di misura
Valutazione dell’incertezza tipo - UNI CEI ENV 13005
Propagazione dell’incertezza per grandezze correlate
La covarianza fra due grandezze aleatorie x e y è espressa:
-
sperimentalmente, si ottiene da M coppie indipendenti di osservazioni simultanee di
due grandezze
M
1
s( x, y ) 
 xi  x  ( yi  y )
( M  1) i 1
-
analiticamente, va espressa la dipendenza di entrambe le variabili da tutte le
grandezze
g h

 u 2 qi 
qi
k 1 qi
P
u ( x, y )  
Misure Meccaniche e Termiche – Anno accademico 2014/15
Incertezza di misura
Valutazione dell’incertezza - UNI CEI ENV 13005
Incertezza estesa
In certe applicazioni commerciali, industriali e normative, e dove sono coinvolte la
salute e la sicurezza pubblica, è necessario dare una valutazione quantitativa
dell’incertezza che definisca un intervallo che comprenda una gran parte dei valori che
possono ragionevolmente essere attribuiti al misurando
ym  U  y ; ym  U  y 
Incertezza estesa:
U ( y)  k  u( y)
richiede la conoscenza completa della distribuzione di probabilità (es: livelli di
confidenza di una gaussiana)
Misure Meccaniche e Termiche – Anno accademico 2014/15
Incertezza di misura
Valutazione dell’incertezza - UNI CEI ENV 13005
Procedura di valutazione - Sommario
1) Si esprime la relazione matematica tra il misurando Y e le grandezze di ingresso Xi:
Y = f(X1, X2,…, XN)
2) Si determina xi, valore stimato della grandezza Xi, tramite analisi statistica di serie
di osservazioni o tramite altri metodi
3) Si valuta l’incertezza tipo u(xi) ci ciascuna stima di ingresso xi, secondo un
approccio di tipo A (analisi statistica di osservazioni) o di tipo B (informazioni)
4) Si valutano le covarianze associate alle stime di ingresso eventualmente correlate
5) Si stima y tramite f, usando le stime xi (punto 2)
6) Si determina l’incertezza tipo u(y) dalle incertezze tipo e dalle covarianze associate
alle stime d’ingresso
7) Se è necessario definire un’incertezza estesa U(y), si ricava k usando la
distribuzione definita per y e il livello di confidenza richiesto
Misure Meccaniche e Termiche – Anno accademico 2014/15
Incertezza di misura
Propagazione delle incertezze
Esempio: dinamometro (misura della potenza trasmessa ad un albero rotante)
Y  f ( X 1 , X 2 ,..., X N )
2
 f  2
 u ( xi )
uc ( y )   

x
i 1 
i 
N
Potenza
W
2RFL
t
o hp 
2RFL
550t
R=giri dell’albero nel tempo t
F=forza del braccio L=lung. braccio
t=tempo di rotazione
Incertezza di misura
Propagazione delle incertezze
Esempio dinamometro - Valutazione delle incertezze
Contatore di giri: digitale, errore massimo: ±1 giro
Determinazione di t: esperienza, ±0.5 s con livello di confidenza del 95%
Misura del braccio L: esperienza, ±1 mm con livello di confidenza del 95%
Misura dello forza F: incertezza di taratura della cella di carico: ±0.2 N (vibrazioni e
oscillazioni dell’indicatore trascurabili)
Misure Meccaniche e Termiche – Anno accademico 2014/15
Incertezza di misura
Propagazione delle incertezze
Esempio dinamometro - Valutazione dell’incertezza totale
R = 1202 ±1.0 rivoluzioni
L = 0.397 ± 0.001 m
F = 45 ± 0.2 N
t = 60 ± 0.50 s
W KLR 2 (0.397)(1202)


 49.972 W/N
F
t
60
W KLF 2 (45)(0.397)


 1.871 W/N
R
t
60
W KFR 2 (45)(1202)


 5664.292 W/m
L
t
60
W KFLR 2 (45)(0.397)(1202)


 37.479 W/s
t
t
602
Misure Meccaniche e Termiche – Anno accademico 2014/15
Incertezza di misura
Propagazione delle incertezze
Esempio dinamometro - Valutazione dell’incertezza totale
uc ( y)  (9.9944) 2  (1.87) 2  (5.6643) 2  (18.7395) 2  22.060 W
livello di confidenza al 95%
Problema inverso: si vuole misurare W con incertezza dello 0.5%
Metodo degli effetti uguali
u ( xi ) 
uc ( y )
f
n
xi
Misure Meccaniche e Termiche – Anno accademico 2014/15
Incertezza di misura
Propagazione delle incertezze
Esempio dinamometro - Valutazione dell’incertezza totale
Metodo degli effetti uguali – calcolo delle accuratezze singole
F 
(2248.724)(0.005)
 0.112 N
4 49.972
R 
(2248.724)(0.005)
 3.004 rad
4 1.871
L 
(2248.724)(0.005)
 0.001 m
4 5664.292
t 
(2248.724)(0.005)
 0.150 s
4 37.479
Misure Meccaniche e Termiche – Anno accademico 2014/15
Caratteristiche statiche
Sensibilità statica
Derivata della curva di taratura in ogni suo punto
Determinazione: effettiva uscita fisica dello
strumento
Es: nel manometro, °/kPa (rotazione angolare/
pressione)
Permette il confronto fra strumenti, riguardo la
capacità di “sentire” variazioni di grandezze di
ingresso
Misure Meccaniche e Termiche – Anno accademico 2014/15
Caratteristiche statiche
Sensibilità statica
Sensibilità dello strumento a ingressi interferenti e/o modificanti
Ingresso interferente
deriva di zero
Ingresso modificante
deriva di sensibilità
Deriva di zero: ingresso int. variato a ing. nullo
Deriva di sensibilità: ripetizione taratura per
valori diversi dell’ingresso modificante
Misure Meccaniche e Termiche – Anno accademico 2014/15
Caratteristiche statiche
Linearità
Linearità indipendente:
Definizione:
Utilizzando la retta di riferimento ottenuta con
l’interpolazione ai minimi quadrati –
Misura della deviazione massima in qualsiasi
punto di taratura dalla retta considerata
Espressione:
- percentuale della lettura
- percentuale di fondo scala
- combinazione:
±A % della lettura o ±B% della lettura (maggiore)
In strumenti lineari: linearità = accuratezza
Misure Meccaniche e Termiche – Anno accademico 2014/15
Caratteristiche statiche
Isteresi
Tipi di attrito:
(a)
(b)
(c)
(d)
attrito interno, smorzamento isteretico
attrito interno, campo di misura pos e neg
attrito esterno, giochi
attrito esterno, giochi, campo di misura pos
e neg
(e) attriti combinati
Importanza della cadenza temporale delle prove
per effetti di rilassamento e/o recupero
Effetto specificato come percentuale di fondo
scala
Misure Meccaniche e Termiche – Anno accademico 2014/15
Caratteristiche statiche
Soglia, Rumore di fondo, Risoluzione, Spazio morto
Soglia La più piccola variazione “apprezzabile” o “misurabile” incrementando
l’ingresso dallo zero
Rumore di fondo Limite inferiore dovuto a fluttuazioni casuali vicine allo zero
(di solito espresso in RMS)
Risoluzione
La più piccola variazione apprezzabile o
misurabile incrementando l’ingresso da un
valore non nullo
Misure Meccaniche e Termiche – 2014/15
qO
RqO
RqI
qI
Caratteristiche statiche
Leggibilità della scala, Campo di misura
Leggibilità della scala
Strumenti analogici: lettura effettuata da un osservatore
Caratteristica dipendente dallo strumento e dall’osservatore
Campo di misura
Intervallo che uno strumento è in grado di misurare
Limite operativo inferiore – Limite operativo superiore
Per strumenti lineari: campo operativo lineare
Segnali tempovarianti: campo dinamico dB=20logN (rapporto fra segnale massimo
e minimo, es: 60 dB 1000:1)
Misure Meccaniche e Termiche – Anno accademico 2014/15
Caratteristiche statiche
Definizioni – UNI 4546
Campo di misura “Intervallo comprendente i valori di misura che si possono
assegnare tramite un dispositivo di misurazione”
Portata “Limite superiore del campo di misura”
Sensibilità “Pendenza della curva di taratura in un suo punto”
Risoluzione “Attitudine di un dispositivo per misurazione a risolvere stati diversi del
misurando”
Ripetibilità “Attitudine di uno strumento a fornire valori di lettura poco differenti fra
loro in letture consecutive eseguite indipendentemente sulla stessa misura”
Misure Meccaniche e Termiche – Anno accademico 2014/15
Caratteristiche statiche
Definizioni – UNI 4546
Stabilità “Attitudine di uno strumento a fornire valori di lettura differenti tra loro in
letture eseguite indipendentemente sullo stesso misurando in un intervallo di tempo
definito”
Isteresi “Proprietà di uno strumento di fornire valori di lettura diversi in
corrispondenza di un medesimo misurando quando questo viene fatto variare per
valori crescenti e per valori decrescenti”
Misure Meccaniche e Termiche – Anno accademico 2014/15
Effetti di inserzione
Impedenza e ammettenza generalizzate
Variabili di sforzo e di flusso
L’utilizzo di uno strumento di misura è associato a una sottrazione di energia, o di
potenza, che provoca, tra l’altro, una variazione del misurando
Ai trasferimenti di energia sono in genere associate due variabili, una di sforzo qs e
una di flusso qf tali che il loro prodotto è una potenza:
p = q s qf
Misure Meccaniche e Termiche – Anno accademico 2014/15
Effetti di inserzione
Impedenza generalizzata
Misura di una variabile di sforzo
Si definisce impedenza generalizzata d’ingresso il rapporto fra una variabile di sforzo
e una di flusso:
z gi 
qs
qf
la potenza sottratta dallo strumento diventa:
qs2
Ps 
z gi
occorre minimizzare zgi relativamente all’impedenza di uscita dello strumento che
precede nella catena di misura
Misure Meccaniche e Termiche – Anno accademico 2014/15
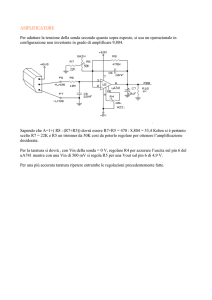
Effetti di inserzione
Impedenza generalizzata
Voltmetro
G
R1
RV
I
VI=R1I
R
Tensione ai capi della resistenza, indisturbata
1
1
1

R1 RV

R1 RV
R1  RV
(collegando il voltmetro, impedenza generalizzata Rv)
Misure Meccaniche e Termiche – Anno accademico 2014/15
Effetti di inserzione
Impedenza generalizzata
Voltmetro
Tensione effettivamente misurata
Vm 
R1 RV
1
I
I
R
R1  RV
1
1
RV
Se Rv (impedenza generalizzata di ingresso del voltmetro) è molto più grande di R1
Vm 
1
R1
1
RV
I  R1 I  VI
Misure Meccaniche e Termiche – Anno accademico 2014/15
Effetti di inserzione
Ammettenza generalizzata
Misura di una variabile di flusso
Si definisce ammettenza generalizzata d’ingresso il rapporto fra una variabile di
flusso e una di sforzo:
y gi 
qf
qs
la potenza sottratta dallo strumento diventa:
Ps  qs q f 
q 2f
y gi
occorre rendere massima ygi relativamente all’ammettenza di uscita dello strumento
che precede nella catena di misura
Misure Meccaniche e Termiche – Anno accademico 2014/15
Effetti di inserzione
Ammettenza generalizzata
RA
Amperometro
II 
Im 
V
R1
Corrente indisturbata
G
V
V / R1

R1  RA 1  RA / R1
R1
(amperometro)
Se RA è molto minore di R1, la corrente misurata tenderà al valore indisturbato
Misure Meccaniche e Termiche – Anno accademico 2014/15