Dipartimento di Ingegneria Industriale dell’Università di Parma – Ing. Giorgio Toderi
Dimensionamento di un condensatore di vapore acqueo
Si deve dimensionare un condensatore che andrà inserito in una macchina a vapore a circuito chiuso.
I dati forniti dal committente sono: portata di vapore [Gv = 80 kg/s ] , titolo del vapore [x = 0.96] e
l’indicazione che il condensatore può essere raffreddato con acqua di fiume.
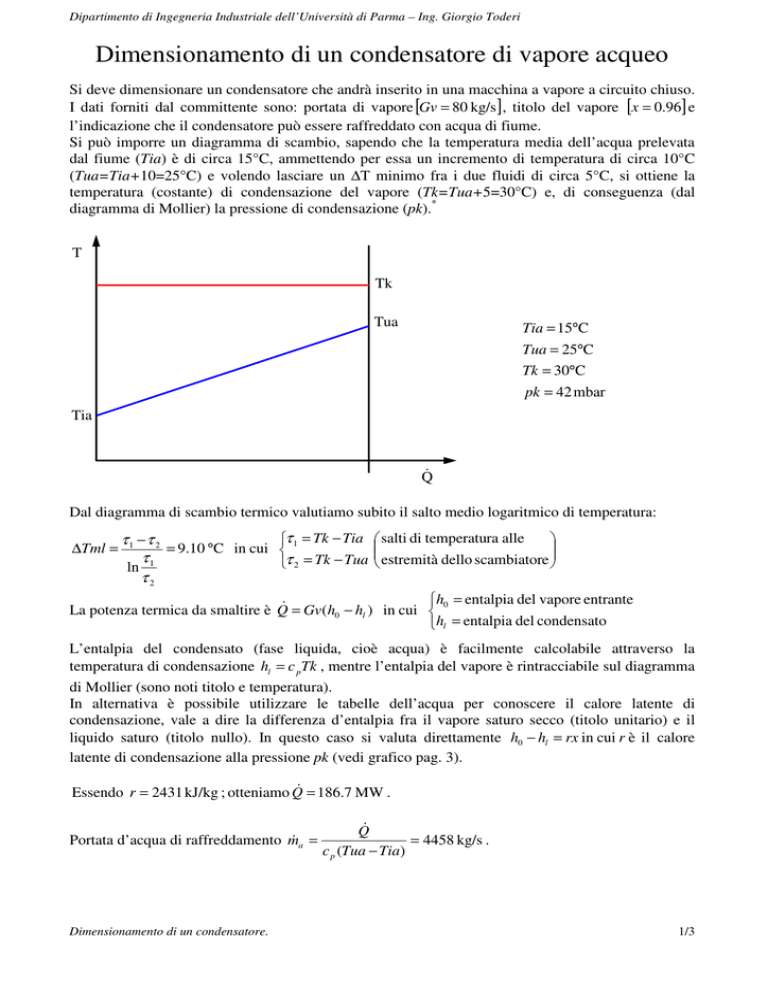
Si può imporre un diagramma di scambio, sapendo che la temperatura media dell’acqua prelevata
dal fiume (Tia) è di circa 15°C, ammettendo per essa un incremento di temperatura di circa 10°C
(Tua=Tia+10=25°C) e volendo lasciare un ∆T minimo fra i due fluidi di circa 5°C, si ottiene la
temperatura (costante) di condensazione del vapore (Tk=Tua+5=30°C) e, di conseguenza (dal
diagramma di Mollier) la pressione di condensazione (pk).*
T
Tk
Tua
Tia = 15°C
Tua = 25°C
Tk = 30°C
pk = 42 mbar
Tia
Q
Dal diagramma di scambio termico valutiamo subito il salto medio logaritmico di temperatura:
∆Tml =
τ1 −τ 2
= 9.10 °C in cui
τ1
ln
τ2
τ 1 = Tk − Tia salti di temperatura alle
τ 2 = Tk − Tua estremità dello scambiatore
La potenza termica da smaltire è Q = Gv(h0 − hl ) in cui
h0 = entalpia del vapore entrante
hl = entalpia del condensato
L’entalpia del condensato (fase liquida, cioè acqua) è facilmente calcolabile attraverso la
temperatura di condensazione hl = c pTk , mentre l’entalpia del vapore è rintracciabile sul diagramma
di Mollier (sono noti titolo e temperatura).
In alternativa è possibile utilizzare le tabelle dell’acqua per conoscere il calore latente di
condensazione, vale a dire la differenza d’entalpia fra il vapore saturo secco (titolo unitario) e il
liquido saturo (titolo nullo). In questo caso si valuta direttamente h0 − hl = rx in cui r è il calore
latente di condensazione alla pressione pk (vedi grafico pag. 3).
Essendo r = 2431 kJ/kg ; otteniamo Q = 186.7 MW .
Portata d’acqua di raffreddamento ma =
Dimensionamento di un condensatore.
Q
= 4458 kg/s .
c p (Tua − Tia )
1/3
Dipartimento di Ingegneria Industriale dell’Università di Parma – Ing. Giorgio Toderi
Imponiamo la velocità con cui l’acqua di raffreddamento deve attraversare il fascio tubiero1.
Un valore tipico è v = 2 m/s; con tale valore calcoliamo la sezione di passaggio per l’acqua
m
S a = a = 2.229 m 2 .
ρv
Questa è la sezione totale vista dalla portata d’acqua, vale a dire la sezione interna di un tubo
moltiplicata per il numero di tubi; quindi, scelto il tubo da utilizzare fra quelli commerciali, si può
calcolare il numero di tubi.
d i = 22 mm [diametro interno]
Si sceglie un tubo 22 x1.5, quindi: s = 1.5 mm [spessore della parete] ;
d e = 25 mm [diametro esterno]
4S a
= 5865 .
π d i2
Noto il materiale con cui è realizzato il tubo scelto (tipicamente rame, per questo tipo di macchina) è
noto anche il suo coefficiente di conduzione, mentre i coefficienti di convezione sulle facce interna
ed esterna si valutano tramite l’uso di tabelle.
di conseguenza si calcola il numero di tubi nt =
λ = 395 W/mK [coefficiente di conduzione della parete]
Si ponga, ad esempio: α i = 2000 W/m 2 K [coefficiente di convezione lato interno] .
α e = 7000 W/m 2 K [coefficiente di convezione lato esterno]
Con tali valori si calcola il coefficiente globale di scambio termico riferito alla superficie interna,
1
applicando i coefficienti correttivi validi per la geometria cilindrica: K =
.
1 di s di
1
+
+
α e d e λ d ml α i
d − di
Essendo d ml = e
= 23.47 mm [diametro medio logaritmico] si ha K=1589 W/m2K.
d
ln e
di
La superficie di scambio dovrà allora essere: S =
Q
= 1.290 ⋅10 4 m 2 .
K ∆Tml
Conseguentemente la lunghezza dei tubi Lt1 =
p
1
S
= 31.84 m .
π d i nt
I tubi sono disposti a ranghi sfalsati, quindi il centro di ciascun tubo
occupa il vertice di un triangolo equilatero il cui lato è pari al passo
3 p2
p, e la cui area è A0 =
. Tale area è quella frazione della
4
piastra tubiera che serve a portare mezzo tubo (60° di ciascuno dei
tre raffigurati). Per ogni tubo sarà quindi necessaria una superficie
3p2
la cui area è A1 =
. Assumendo p = 1.5 d e che è un valore
2
Calcolata la portata, questa può essere ottenuta adottando alta velocità e piccola sezione di passaggio, o, viceversa,
grande sezione e bassa velocità. Nel primo caso si ottiene una macchina più piccola (minore costo d’investimento) e
maggiori perdite di carico per l’attraversamento del fascio tubero (maggiore costo d’esercizio per la pompa di
circolazione) nel secondo caso si hanno maggiore investimento e minori costi d’esercizio. La scelta ottimale è,
ovviamente, una via di mezzo.
Dimensionamento di un condensatore.
2/3
Dipartimento di Ingegneria Industriale dell’Università di Parma – Ing. Giorgio Toderi
tipico, per questa macchina, si può allora stimare approssimativamente il diametro della piastra
tubiera: D f 1 =
2 3 p 2 nt
π
= 3.016 m .
Realizzando il condensatore a più passaggi la sua lunghezza diminuisce, mentre il diametro
aumenta. Realizzando due passaggi, per esempio, dovremo mandrinare sulle piastre tubiere, non nt
tubi, ma 2nt mezzi tubi; ne consegue che la distanza fra le due piastre dimezza, mentre raddoppia la
loro area determinando un aumento del diametro di un fattore pari alla radice quadrata di 2. Più
generalmente si può osservare che esiste un legame di proporzionalità diretta fra area della piastra e
numero dei passaggi; legame che è, invece, di proporzionalità inversa, per la lunghezza.
In parole povere, realizzando lo scambiatore a n passaggi avremo
D fn = n D f 1
Ltn =
Lt1
n
Nel nostro caso si trova che Lt1>10 Df1, quindi, per ottenere una macchina più compatta, conviene
realizzare più passaggi. Precisamente con due passaggi si ottiene Lt2=15.92 m e Df2=4.265 m, con tre
passaggi si ottiene Lt3=10.61 m e Df3=5.223 m.
Ltn
<5.
D fn
2480
125
2470
115
2460
105
2450
95
2440
85
2430
75
2420
65
2410
55
2400
45
2390
35
2380
25
2370
Pressione di condensazione [mbar].
Calore latente [kJ/kg]
Salvo casi particolari si cerca di fare in modo che risulti 2 <
15
15
20
25
30
35
40
45
50
Temperatura di condensazione [°C]
*
Attenzione! Pk potrebbe essere fissato, vale a dire un dato del problema, in tal caso da questo si dovrà ricavare
Tk, il che potrebbe vincolare alcune scelte. Ricordate sempre che, in ogni caso, i valori assunti da Pk, Tk, r sono
sempre legati assieme, come si vede dal grafico in questa pagina.
Dimensionamento di un condensatore.
3/3










