Macchina sincrona anisotropa

Macchina sincrona a poli salienti Macchina sincrona a poli salienti (anisotropa)
1. Generalità e schematizzazione del campo
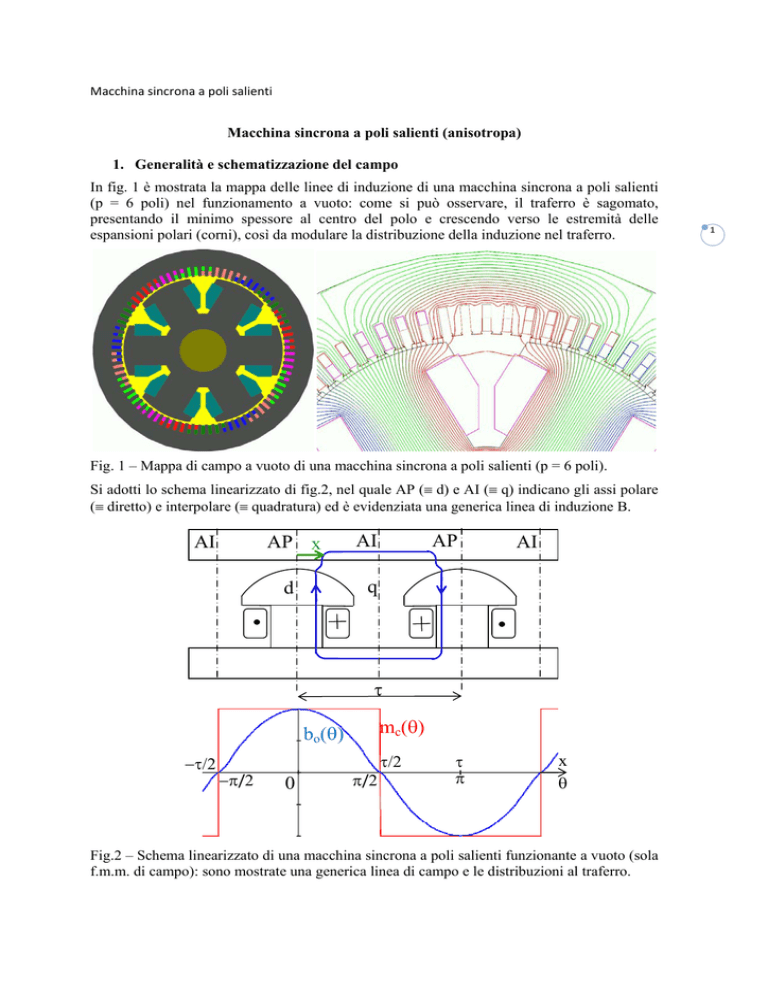
In fig. 1 è mostrata la mappa delle linee di induzione di una macchina sincrona a poli salienti
(p = 6 poli) nel funzionamento a vuoto: come si può osservare, il traferro è sagomato,
presentando il minimo spessore al centro del polo e crescendo verso le estremità delle
espansioni polari (corni), così da modulare la distribuzione della induzione nel traferro.
Fig. 1 – Mappa di campo a vuoto di una macchina sincrona a poli salienti (p = 6 poli).
Si adotti lo schema linearizzato di fig.2, nel quale AP ( d) e AI ( q) indicano gli assi polare
( diretto) e interpolare ( quadratura) ed è evidenziata una generica linea di induzione B.
AI
AP x
AI
d
q
AP
AI

mc()
bo()
/2 /2 0
/2
/2


x
 Fig.2 – Schema linearizzato di una macchina sincrona a poli salienti funzionante a vuoto (sola
f.m.m. di campo): sono mostrate una generica linea di campo e le distribuzioni al traferro.
1
Macchina sincrona a poli salienti Definito  l’angolo elettrico lungo la periferia e x la corrispondente coordinata lineare lungo
la circonferenza interna di statore, vale il seguente legame:
x = (/) ,
dove  è il passo polare, misurato in [m] lungo la circonferenza interna della statore.
Indicata con Mc la f.m.m. di eccitazione (c = campo) attorno a ciascun polo:
Mc = NcIc
dove Nc è il N° spire di ogni bobina di campo e Ic è la corrente continua di eccitazione, per la
distribuzione di f.m.m. mc() al traferro si può scrivere:
+ Mc per /2 <  < + /2
mc() =  Mc per +/2 <  < + 3/2
+ Mc per +3/2 <  < + 5/2 …
Data la simmetria della generica linea di campo disegnata, la legge della circuitazione di
Ampére può essere scritta limitandosi a metà del percorso:
mc() = ug() + ufe()  ug() ,
dove si è supposto che la c.d.t.m. ufe() nei tratti ferromagnetici (corona statore e rotore, denti
statore, corpo polare) sia trascurabile, ovvero che il nucleo ferromagnetico sia lontano dalla
saturazione magnetica. Dunque, considerando la sagomatura dello spessore di traferro (g()),
la distribuzione della induzione a vuoto è data da:
bo() = oug()/g()  omc()/g() .
Questa espressione mostra che, pur di sagomare il traferro, si può partire da una distribuzione
rettangolare di f.m.m. mc() per ottenere una distribuzione prossima alla sinusoidale per la
induzione al traferro bc(). Infatti, trascurando la presenza delle cave, per avere
bo() = Bcos()
il traferro dovrebbe idealmente essere sagomato come segue:
g() = oug()/bo()  (oMc/B) / cos() ;
in tal modo, il valore minimo di traferro gmin = g(0) si ha al centro del polo, mentre sull’asse q
il traferro dovrebbe essere teoricamente infinito.
Naturalmente questa distribuzione del traferro è realizzabile sono in modo approssimato:
pertanto, la distribuzione di B risulta alternata, ma solo approssimativamente sinusoidale,
come mostrato in fig.2 (dove le scale di mc() in [A/m] e di bo() in [T/m] sono state scelte in
modo da far coincidere i valori di picco delle due curve).
Possiamo dunque sottolineare le due principali differenze rispetto alla macchina sincrona
isotropa: f.m.m. a distribuzione rettangolare e traferro non costante.
D’altra parte la f.m.m. di indotto, dovuta al funzionamento a carico, è a distribuzione
sinusoidale e quindi associabile ad un fasore spaziale: pertanto, la f.m.m. di induttore e quella
di indotto, aventi distribuzioni spaziali diverse, non sono direttamente confrontabili. Per
studiare il comportamento della macchina, dunque, tali distribuzioni si dovrebbero sommare
punto a punto lungo la periferia, come pure la distribuzione di induzione dovrebbe essere
determinata punto a punto. Questa procedura risulta poco adatta allo sviluppo di un modello
per lo studio del funzionamento in termini di equazioni circuitali elettriche.
Si adotta, dunque, un diverso approccio, che va sotto il nome di teoria dei due assi.
2
Macchina sincrona a poli salienti 2. Funzionamento a vuoto (solo induttore percorso da corrente)
Come si è visto, a fronte di una f.m.m. di eccitazione mc() a distribuzione rettangolare ( ),
la corrispondente distribuzione di induzione bo() risulta pressoché sinusoidale ().
A quest’ultima distribuzione è dunque possibile associare un fasore spaziale flusso di polo,
avente la direzione del picco B della distribuzione bo(), il verso del polo Nord (semionda
positiva di bo()) e la ampiezza  data da:
 2


B  cos  x          dx   
 2
 2

B  cos      
 2
d 2
  B  ,
 
dove  è la lunghezza assiale del pacco lamiere di statore.
Dunque, il fasore flusso concatenato dell’avvolgimento di fase è dato da:
 = ka Ns/2= Nse/2
con ka fattore di avvolgimento, Ns = N° di spire in serie dell’avvolgimento di fase, Nse = kaNs
N° di spire efficaci di tale avvolgimento; la presenza del 2 è dovuta al fatto che il fasore è
espresso in valore di picco, mentre è espresso in valore efficace.
Adottando il segno negativo nella scrittura della legge della induzione (cioè legando il verso
della f.e.m. a quello del flusso con la regola della vite destrorsa), il fasore f.e.m. di fase a
vuotoEof è esprimibile come:
Eof = j 
dove  è la pulsazione elettrica, legata alla velocità meccanica  [radmecc/s] da:  = p/2.
Nel piano della macchina (rappresentata a 2 poli, così che gli angoli meccanici appaiano
anche come elettrici), vale la rappresentazione fasoriale di fig.3; nella stessa figura è mostrata
anche la caratteristica di magnetizzazione a vuoto, sia in assenza di saturazione (retta g), che
in presenza di nucleo ferromagnetico saturabile (curva affetta da ginocchio).
Eof
Eof
g
q , d
Mc  Mc
Fig. 3 – Diagramma fasoriale relativo al funzionamento a vuoto della macchina e
corrispondente caratteristica di magnetizzazione.
3
Macchina sincrona a poli salienti 3. Reazione di indotto (solo indotto percorso da corrente)
Quando l’indotto sia percorso da un sistema di correnti equilibrate sinusoidali nel tempo, si
genera una f.m.m. a distribuzione sinusoidale nello spazio, cioè un campo di f.m.m. rotante
(campo magnetico di G. Ferraris): esso è associabile ad un fasore spaziale f.m.m. di
indottoMi proporzionale al fasore corrente efficace di faseI:
Mi = kM I ,
con kM = (32/)(Nse/n) .
Il fasore f.m.m. di indottoMi può essere orientato nello spazio in una direzione e in un verso
qualsiasi, in relazione alla modalità di funzionamento della macchina. Indicato con  l’angolo
di reazione come mostrato in fig. 4 (ovvero di ritardo della f.m.m. di indotto rispetto all’asse
interpolare q: 0   < 2), si hanno le seguenti due componenti di f.m.m. di indotto:
 f.m.m. torcente (associata alla coppia elettromagnetica): Miq = Micos();
 f.m.m. smagnetizzante (associata ad un effetto smagnetizzante): Mid = Misin().
Miq
q 
Mi
d
Mid
Fig. 4 – Funzionamento con solo indotto percorso da corrente: f.m.m. di indotto e sua
scomposizione sui due assi.
Si studia separatamente l’effetto della reazione di indotto sugli assi d e q: va osservato che,
partendo da distribuzioni sinusoidali di f.m.m., le distribuzioni spaziali delle corrispondenti
componenti di induzione non hanno distribuzione sinusoidale, perché il traferro sagomato
delle espansioni produce un effetto distorcente sulla forma d’onda spaziale.
Nelle figure seguenti sono evidenziate le correnti nelle cave statoriche: i simboli X e , di
dimensioni graduate, rappresentano il verso e la intensità delle correnti totali distribuite nelle
cave, a prescindere dalla appartenenza dei lati attivi in cava a ciascuna delle tre fasi.
La mappa delle linee di campo relativa alla reazione di asse d viene qui omessa perché,
avendo l’asse magnetico della f.m.m. lungo tale asse, si presenta abbastanza simile a quella
mostrata in fig. 1. Per quanto riguarda le distribuzioni lungo il traferro, in fig. 5 è
rappresentata la condizione di reazione di asse d: al traferro agisce una f.m.m. di indotto
mid(), a distribuzione spaziale sinusoidale, con ampiezza Mid e asse magnetico lungo l’asse
d. La sagomatura del traferro implica che la conseguente distribuzione di induzione, bid(),
risulti distorta. Si noti che in fig. 5, come in precedenza, si sono adottate opportune scale in
[A/m] e [T/m], che consentono di far coincidere i valori di picco di mid() e di bid().
4
Macchina sincrona a poli salienti Le caratteristiche costruttive dell’avvolgimento trifase distribuito di indotto lo rendono
sensibile al campo principale di induzione al traferro, mentre l’effetto “ai morsetti” dei campi
armonici superiori (ovvero l’ampiezza delle corrispondenti f.e.m. armoniche) risulta
fortemente attenuato: pertanto, della curva bid() è utile considerare la sola armonica
fondamentale, in figura indicata con bd(). In base alla forma d’onda di bid(), è intuitivo
riconoscere che il valore di picco di bd() è inferiore al valore di picco di bid().
Naturalmente, essendo la bd() a distribuzione sinusoidale, essa si può interpretare come
dovuta ad una f.m.m. di reazione, Md, a distribuzione spaziale rettangolare: in base alla già
citata scelta delle scale, la f.m.m. Md risulta posizionata sul picco della bd().
Si definisce coefficiente cd di reazione di asse d (tipicamente: cd  0.85) il rapporto:
cd = Md / Mid .
In modo simile a quanto già visto nel funzionamento a vuoto, si può scrivere:
d = ka Nsd/2= Nsed/2 ,
Ed = j d .
Mid
Md
bd()
mid()
bid()
 AP
AI
   q
  AI
x
 d
x
x x
x x
q
Fig. 5 – Reazione di armatura sull’asse d: distribuzioni di indotto e distribuzioni di reazione.
La mappa delle linee di campo della reazione di indotto agente lungo l’asse q è mostrata in
fig. 6: come si nota, tali linee si richiudono lungo la scarpa polare: per evitare saturazioni
locali, specialmente in corrispondenza dei corni delle espansioni, è dunque necessario che tali
corni abbiano spessore adeguato in corrispondenza dell’attacco con il corpo del polo.
In fig. 7 sono rappresentate le distribuzioni relative alla reazione di asse q: al traferro agisce
una f.m.m. di indotto miq(), a distribuzione spaziale sinusoidale, con ampiezza Miq e asse
magnetico lungo l’asse q. La sagomatura del traferro implica che la conseguente distribuzione
di induzione, biq(), risulti distorta.
Si noti che in fig. 7 si sono adottate opportune scale in [A/m] e [T/m], che consentono di far
5
Macchina sincrona a poli salienti coincidere le pendenze di miq() e di biq() per  = 0 (e quindi anche per  = ). Questa
condizione può apparire difforme da quella di fig. 5, ma in realtà è congruente: infatti, se si
supponesse traferro uniforme pari a gmin (macchina isotropa), in entrambi i casi si avrebbe la
sovrapposizione di sinusoidi (mid() sovrapposta a bid(); miq() sovrapposta a biq()).
6
Fig. 6 - Reazione di armatura sull’asse q: mappa di campo delle linee di induzione
Anche in questo caso, le caratteristiche costruttive dell’avvolgimento trifase distribuito di
indotto lo rendono sensibile al campo principale di induzione al traferro, mentre l’effetto “ai
morsetti” dei campi armonici superiori (ovvero l’ampiezza delle corrispondenti f.e.m.
armoniche) risulta fortemente attenuato: pertanto, della curva biq() è utile considerare la sola
armonica fondamentale, in figura indicata con bq(). In base alla forma d’onda di biq(), è
intuitivo riconoscere che il valore di picco di bq() è superiore al valore di picco di biq().
Miq
miq()
biq()
bq()
AP
   d
  Mq

AI
AP
x
 q
x
x x
x x
d
Fig. 7 - Reazione di armatura sull’asse q: distribuzioni di indotto e distribuzioni di reazione.
Macchina sincrona a poli salienti Naturalmente, essendo la bq() a distribuzione sinusoidale, essa si può interpretare come
dovuta ad una f.m.m. di reazione, Mq, a distribuzione spaziale rettangolare: in base alla già
citata scelta delle scale, la f.m.m. Mq risulta posizionata sul picco della bq().
Si definisce coefficiente cq di reazione di asse q (tipicamente: cq  0.35) il rapporto:
cq = Mq / Miq .
In modo simile a quanto già visto nel funzionamento a vuoto, si può scrivere:
q = ka Nsq/2= Nseq/2 ,
Eq = j q .
Sulla base delle precedenti considerazioni, si possono tracciare le caratteristiche di
magnetizzazione relative alla reazione di asse d e di asse q. Per la reazione di asse d, vale la
caratteristica Ed = Ed(Md) di fig. 8 (il cui andamento coincide con quello di fig. 3, essendo
coinvolto lo stesso circuito magnetico saturabile, lungo l’asse d).
Viceversa, per la reazione di asse q si ha la caratteristica Eq = Eq(Mq) di fig. 8: il suo
andamento è praticamente lineare, con pendenza inferiore a quella del tratto lineare di Ed =
Ed(Md) (coincidente con la caratteristica di traferro g di fig. 5): la linearità di Eq = Eq(Mq)
è dovuta all’entità rilevante del traferro equivalente nella zona interpolare, che limita
l’ampiezza del flusso di reazione d’asse q (q) e ne linearizza il legame con Mq.
Ed
Eq
Md , Mq
Fig. 8 – Caratteristica di magnetizzazione di reazione lungo l’asse d e lungo l’asse q.
4. Funzionamento a carico (simultanea presenza di eccitazione e reazione)
Se si vuole studiare il funzionamento a carico tenendo conto della non linearità della
caratteristica di magnetizzazione lungo l’asse d, è necessario seguire la procedura descritta nel
seguito (si supponga di partire dalla conoscenza delle cause – correnti, f.m.m. –) per giungere
a determinare gli effetti -f.e.m., c.d.t, tensione ai morsetti-):
 si deve conoscere l’angolo di reazione  di fig.4, cui consegue la scomposizione della
f.m.m. di indottoMi = kM I nei suoi componentiMid = kM Id e Miq = kM Iq;
 mediante i fattori di reazione cd e cq, si determinano le corrispondenti f.m.m. di
reazioneMd = cd Mid e Mq = cq Miq;
 si determina il fasore f.m.m.ME risultante agente lungo l’asse d (ME = Mc +Md );
 con la ampiezza ME diME si entra in ascissa sulla caratteristica a vuoto di fig. 3,
ricavando in ordinata l’ampiezza della f.e.m. risultanteE;
 entrando con la ampiezza Mq diMq nella caratteristica di fig. 8, si determina la
ampiezza Eq dellaEq;
7
Macchina sincrona a poli salienti  si determina la f.e.m.Ea =  jXa I corrispondente alla c.d.t. sulla reattanza Xa di
dispersione (poiché è associata alla dispersione di statore, non risente della anisotropia);
 si determina la c.d.t. resistiva Rs I sulla resistenza di fase di statore;
 si calcola il fasore tensione di fase: Vf =E +Eq +Ea  Rs I .
Questa sequenza, nella quale è compreso un passaggio non lineare attraverso la caratteristica
di magnetizzazione, sta alla base della procedura detta costruzione di Arnold-Blondel.
Nel seguito, invece, si sviluppa la trattazione linearizzata, che va sotto il nome di costruzione
delle due reattanze: a tale scopo, si adottino le caratteristiche di magnetizzazione linearizzate
(caratteristica di traferro sull’asse d, caratteristica di asse q).
Per ora si suppongano ancora come note la f.m.m. di campoMc e quella di indottoMi (e
quindi anche l’angolo di reazione ), e si voglia giungere a ricostruire la tensione di faseVf.
Se la macchina si può trattare come sistema lineare, allora vale il principio di sovrapposizione
delle cause e degli effetti. Si può dunque istituire la seguente formulazione concettuale:
Etot = ƒ(Mtot ) = ƒ(hMh ) = h ƒ(Mh ) = hEh(Mh ) ,
ovvero si può determinare la f.e.m. totale dovuta alla risultante di tutte le f.m.m. agenti come
la somma delle f.e.m. dovute singolarmente a ciascuna f.m.m. supposta agente da sola.
Vale dunque il diagramma fasoriale rappresentato in fig. 9 (dove non è evidenziata la c.d.t.
resistiva Rs I, spesso piccola, come tipico per macchine di taglia medio-grande).
Eo
d
Eo
q
Ed
Eq
Mecc
Mc
d
Ed
q E Ea
q
Miq  Vf   
I
Mi
Mid
Md Mc Mq
Fig. 9 – Diagramma fasoriale per la costruzione delle due reattanze e caratteristiche
linearizzate di magnetizzazione dei due assi. In considerazione dell’ipotesi di linearità, è conveniente introdurre opportuni parametri di
proporzionalità tra le componenti di corrente e le corrispondenti componenti di f.e.m.; in
regime sinusoidale, tali parametri sono delle reattanze. Pertanto si può scrivere:
Vf =Eo +Ed +Eq +Ea  Rs I = Eo  jXd Id  jXq Iq  jXa I  Rs I .
I parametri Xd e Xq sono denominati rispettivamente reattanza di reazione longitudinale (o
di asse d) e reattanza di reazione trasversale (o di asse q); se poi osserva che:
I = Id +Iq ,
(dove per le ampiezze si ha: Id = Isin(); Iq = Icos()) la precedente equazione fasoriale si
può riscrivere come segue:
8
Macchina sincrona a poli salienti Vf =Eo  jXd Id  jXq Iq  Rs I ,
dove le quantità
Xd = Xd + Xa ,
Xq = Xq + Xa
sono denominate reattanze sincrone, rispettivamente di asse d e di asse q.
In fig. 9, oltre all’angolo di reazione , sono evidenziati:
 l’angolo  di sfasamento tra i fasori tensioneVf e correnteI ( è assunto positivo se di
ritardo della corrente rispetto alla tensione);
 l’angolo  tra la tensione di faseVf e la f.e.m. a vuotoEo , detto anche angolo di carico (in
quanto diverso da zero solamente con funzionamento a carico; infatti, a vuotoI = 0, da cui
consegue:Vf =Eo , e quindi:  = 0);
 l’angolo  tra la f.m.m.Mc di campo e la f.m.m.Mi di indotto.
Naturalmente si ha:
=+ ;
 =  + /2 .
Noti i parametri di asse d e q, è possibile studiare il funzionamento a carico della macchina,
partendo dalla conoscenza di Vf, I, , per risalire a Eo e quindi alla corrente di eccitazione Ic:
per far ciò è però necessario determinare la posizione dell’asse q, al fine di scomporre la
corrente I nelle componenti Id e Iq.
A tal fine, si consideri il diagramma fasoriale di fig. 10, dove per i fasori ivi indicati si ha:
Eo =Vf + jXa I + jXq Iq + jXd Id =Vf +Va +Vq +Vd .
Si osservi che se non si conosce l’angolo di reazione  non è possibile scomporreI nei
componentiId eIq: pertanto, a partire dalla sola conoscenza diVf eI non è possibile
completare il diagramma.
EoVd
3
VJ
q
2
Vq Va
1
V
f



Ic
d
I
Fig. 10 – Costruzione fasoriale per la determinazione della posizione dell’asse q.
Oltre ai fasoriVf,Va = jXa I,Vq = jXq Iq, eVd = jXd Id di fig.10, si consideri anche
il fasoreVJ (segmento 2-3) inteso come il prolungamento del fasoreVa (segmento 1-2) fino
a incontrare l’asse q nel punto 3. Con considerazioni geometriche, si constata che l’angolo tra
i fasoriVJ eVq vale , per cui, per i moduli si può scrivere:
Vq = VJcos().
9
Macchina sincrona a poli salienti D’altra parte si ha: Iq = Icos(), ed essendo Vq = XqIq, si ha:
Vq = XqIq, = XqIcos() = VJcos(),
ovvero:
VJ = XqI,
cioè in termini fasoriali:
VJ = jXq I .
La tensioneVJ è detta “joubertica” (da Joubert, che l’ha introdotta): si tratta di una quantità
fittizia, che non viene direttamente coinvolta nella relazione fasoriale:
Eo =Vf + jXa I + jXq Iq + jXd Id =Vf +Va +Vq +Vd ,
ma tuttavia consente di determinare i singoli contributi di questa.
Infatti, noti i fasoriVf eI, sommandoVa aVf si giunge al vertice 2 di fig. 10;
sommandoVJ = jXq I aVa si giunge al punto 3, che si trova lungo l’asse q.
La conoscenza della orientazione di q nel piano dei fasori di macchina consente la
determinazione di  e quindi il completamento del diagramma fasoriale, con il calcolo di Eo e
dunque della corrente di eccitazione Ic.
Osservando che per il fasoreVJ +Va si ha:
VJ +Va = jXq I + jXa I = jXq I
dove Xq è la reattanza sincrona di asse q, per applicare la costruzione delle due reattanze si
può operare come mostrato in fig. 11 (dove sono anche indicati i versi adottati per gli assi q 
Re e d  Im del piano complesso).
q
Re
Eo jXd Id
jXq I
jXq Iq
Im
Ic

 Vf
  I
d
Fig. 11 – Diagramma fasoriale della costruzione delle due reattanze.
A partire dalla conoscenza dei fasoriVf eI, aVf si somma jXq I, il cui vertice individua
l’orientazione dell’asse interpolare e quindi consente di determinare l’angolo ; calcolatiId
eIq, aVf si sommano jXq Iq e jXd Id, ottenendoEo, da cui si ottiene la corrente di
eccitazione Ic, sulla caratteristica linearizzata di magnetizzazione dell’asse d:
Eo = kEIc .
10
Macchina sincrona a poli salienti 5. Scambio di potenza attiva e reattiva; coppia elettromagnetica.
Si consideri una macchina sincrona trifase a poli salienti nel funzionamento a carico (con le
convenzioni di fig. 12) e si assuma valido il modello linearizzato sviluppato nel paragrafo
precedente.
I
MS
3f
Vf
Pp
Pme
Pel
Fig. 12 – Convenzioni adottate per il funzionamento a carico della macchina sincrona.
Dal punto di vista energetico, si ha:
Pme = Pel + Pp
Pp = PpJs + Ppmecc + Ppfes + Ppecc + Ppadd
dove
sono le perdite totali.
Si supponga idealmente che la macchina sia priva di: perdite negli avvolgimenti di statore PpJs
= 3RsI2, perdite meccaniche Ppmecc, perdite ferromagnetiche di statore Ppfes, perdite di
eccitazione Ppecc e perdite addizionali Ppadd.
Per la potenza apparente trifase ai morsetti si ha:
A = P + jQ = 3 Vf I .
D’altra parte, sulla base del diagramma fasoriale di fig. 10, si può scrivere:
dove si è posto:
Vf = (Eo jXd Id )  jXq Iq =Vfq +Vfd ,
Vfq = Eo jXd Id ; Vfd =  jXq Iq .
Pertanto, per i fasoriId eIq si può scrivere:
Id = (Eo Vfq )/(jXd) ;
Iq = Vfd /(jXq) ,
essendoI =Id +Iq .
Sempre in base al sistema di riferimento adottato in fig. 10, si può scrivere:
Eo = Eo ;
Vf = Vfexp(j) =Vfd +Vfq = jVfsin() + Vfcos() .
Pertanto, per la potenza apparente vale la seguente riformulazione:
A = 3 Vf I = 3  (Vfq +Vfd )( Iq + Id ) =
= 3Vf (cos()jsin())[(Vf/Xq)sin() + j(Eo  Vfcos())/Xd] .
Dalla elaborazione di quest’ultima espressione si ottengono le seguenti espressioni della
potenza attiva e reattiva scambiate ai morsetti di macchina:
P = 3[(EoVf/Xd)sin() + (1/2)(Vf2/Xd)(Xd/Xq  1)sin(2)]
Q = 3(EoVf/Xd)cos()  (Vf2/Xd)[cos2() + (Xd/Xq) sin2()] .
11
Macchina sincrona a poli salienti In modo simile a quanto già fatto per la macchina sincrona isotropa, l’aver trascurato anche in
questo caso le perdite totali ci consente di ritenere che: Pme = Ceo = P + Pp  P, da cui si
ricava la espressione della coppia elettromagnetica Ce  P/o :
Ce = (3/o)[(EoVf/Xd)sin() + (1/2)(Vf2/Xd)(Xd/Xq  1)sin(2)] .
Le espressioni trovate per P, Q, Ce esprimono l’energetica di una macchina sincrona
anisotropa in una modalità di funzionamento in cui sono imposte la tensione e la frequenza ai
morsetti: si tratta della situazione tipica di una macchina funzionante in parallelo ad una rete
che impone, a frequenza costante, una tensione Vf costante.
Tale tipo di rete è anche detta “di potenza infinita”, o “con impedenza interna nulla”).
La natura binomia della coppia elettromagnetica evidenzia le seguenti proprietà:
 il primo addendo della coppia elettromagnetica prende il nome di coppia di eccitazione
Cecc, in quanto, essendo proporzionale a Eo, dipende anche dalla corrente di campo Ic;
 il secondo addendo è denominato coppia di anisotropia Canis, in quanto esiste solamente in
caso di anisotropia, ovvero quando le reattanze sincrone d’asse d e q sono diverse tra loro:
usualmente per il rapporto Xd/Xq si ha: Xd/Xq  23;
 la coppia di anisotropia presenta periodicità doppia della coppia di eccitazione, rispetto
all’angolo di carico ;
 per angoli di carico  < 90°, la coppia di anisotropia da un contributo additivo alla coppia
di eccitazione: questa proprietà è diretta conseguenza del fatto che Xd/Xq >1, condizione
tipica delle macchine dotate di sistema di eccitazione in corrente;
 viceversa, si può mostrare che nelle macchine con eccitazione a magnete permanente, dove
si ha Xd/Xq < 1, sempre per  < 90° il contributo di coppia Canis risulta sottrattivo;
 qualora la macchina non presenti anisotropia (Xd = Xq = X; cd = cq =1), le espressioni di P,
Q, Ce si riducono a quelle già viste per la macchina isotropa.
In fig. 13 è mostrato l’andamento qualitativo dei due contributi di coppia e l’andamento
complessivo della caratteristica pseudo-meccanica di coppia: ne risulta che l’angolo limite
lim di stabilità statica, al di sopra del quale la coppia complessiva decresce al crescere di , è
inferiore a 90°, a differenza di quanto avviene nella macchina sincrona isotropa.
Ce Ctot
Cecc
Canis  [°] 0
30
60
lim
90
120
150
180
Fig. 13 – Caratteristica pseudo-meccanica di coppia della macchina sincrona anisotropa:
l’angolo limite di stabilità statica lim è inferiore ai 90°, tipico delle macchine isotrope.
Le precedenti espressioni di P, Q, Ce possono essere riformulate anche in funzione delle
correnti di campo Ic e di armatura I (ovvero delle rispettive f.m.m. Mc e Mi).
12
Macchina sincrona a poli salienti A tale scopo, si consideri che:
 in linearità la f.e.m. di fase è proporzionale alla corrente di campo, come segue:
Eo = Nse(2/)(1/2)ℓ(o/gmin)Mc =  [Nse(2/)ℓ(o/gmin)] Mc
cioè
Eo = hEMc = hENcIc;
 la f.m.m. di indotto è proporzionale alla corrente di statore secondo la relazione:
Mi = (32/)(Nse/n)I = kMI ;
 inoltre, come già ricavato dal diagramma fasoriale di fig. 10, si ha:
Vfq = Eo jXd Id ; Vfd =  jXq Iq ;
 infine, sempre dal diagramma di fig. 10 risulta:
Eo = Eo ;
Id = jIsin();
Iq = Icos() ;  =   /2 .
Riprendendo e rielaborando l’espressione della potenza apparente, si ha:
A = 3 Vf I = 3  (Vfq +Vfd )( Iq + Id ) =
= 3  (Eo jXd Id  jXq Iq )( Iq + Id ) =
Considerando le precedenti relazioni, per la potenza attiva e reattiva si ottiene:
P = 3EoIsin() + (3/2)(Xd  Xq)I2sin(2)
Q =  3EoIcos()  XdI2cos2() XqI2sin2() ,
e considerando che Eo = hEMc e I = Mi / kM , consegue:
P = 3(hE / kM)McMisin() + (3/2)(Xd  Xq)(Mi / kM)2sin(2)
Q =  3(hE / kM)McMicos()  Xd(Mi / kM)2cos2() Xq(Mi / kM)2sin2() .
Infine, dividendo la espressione della potenza attiva (con macchina ideale a rendimento
unitario) per la velocità di rotazione o = /n, per la coppia elettromagnetica Ce si giunge a:
Ce = Cecc + Canis = 3n(hE/kM)McMisin() + (3/2)n(Ld  Lq)(Mi/kM)2sin(2) .
Per queste espressioni di P, Q, Ce valgono le seguenti osservazioni:
 nonostante il segno negativo esplicito nel primo termine della potenza reattiva, tale termine
è positivo, perché, essendo  > /2, risulta cos()<0;
 sviluppando il rapporto hE/kM, per la coppia di eccitazione Cecc risulta:
Cecc = n2(oℓ/gmin)McMisin() = n2gMcMisin() :
come si osserva, tale coppia esiste in quanto   0, mentre tende a zero se  si annulla: per
tale ragione, tale contributo di coppia viene anche detto coppia di allineamento;
 fissati i valori della corrente di campo Ic e della corrente di armatura I, cioè fissati i valori
di Mc e Mi, la coppia elettromagnetica massima si ha quando  = /2, ovvero quando il
campo di f.m.m. di armatura è orientato in quadratura rispetto a quello di campo: quando la
quadratura è in ritardo, la coppia elettromagnetica è frenante (funzionamento come
generatore, considerato in queste note); quando la quadratura è in anticipo, la coppia
elettromagnetica è motrice e il funzionamento è come motore;
 con  = /2 la coppia di anisotropia Canis si annulla; inoltre, la espressione della potenza
13
Macchina sincrona a poli salienti 
reattiva si semplifica come segue: Q(=/2) =  Xq(Mi/kM)2; infatti, la reazione di indotto,
puramente torcente, non dà alcun effetto magnetizzante o smagnetizzante al traferro e
l’unica potenza reattiva è messa in gioco dalla componente di asse q della reazione, ed è
negativa, quindi assorbita da parte della macchina;
il funzionamento con || = /2 è quello che massimizza la coppia (e quindi la potenza
convertita da meccanica a elettrica o viceversa), a pari valori efficaci delle correnti
circolanti; inoltre anche la potenza reattiva scambiata è modesta (funzionamento quasi a
cos unitario): questa modalità di funzionamento è possibile imponendo che le correnti di
statore producano una f.m.m.Mi di armatura in quadratura con la f.m.m. di campoMc:
questa modalità di funzionamento prende il nome di “orientamento di campo”, ed è resa
possibile dall’impiego di opportuni convertitori elettronici di potenza controllati.
14