Lezioni di Fisica
Raggruppamento misto di resistori
Prof. Ettore Limoli
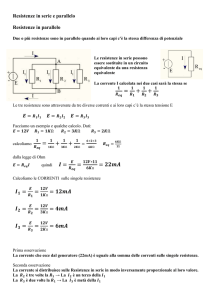
Supponiamo di avere quattro resistori, di resistenza nota (misurata in ohm), collegati come in Figura 1.
È nota, pure, la f.e.m. della pila (misurata in volt) di cui consideriamo trascurabile la resistenza interna.
Figura 1
Il circuito presenta due raggruppamenti in parallelo: R1-R2 ed R3-R4.
I due raggruppamenti sono collegati fra loro in serie.
Per ciascuna resistore ci proponiamo di determinare:
la tensione V ai suoi capi (caduta di potenziale);
la corrente I che lo attraversa;
la potenza P dissipata per effetto Joule.
Ci proponiamo, infine, di determinare la corrente misurata dall’amperometro e la potenza
complessivamente dissipata dal circuito per effetto Joule.
Allo scopo compileremo una tabella contenente i risultati via via conseguiti, iniziamo col porre i valori noti.
La tabella conterrà i valori di ciascuna grandezza in corrispondenza degli indici di riferimento dei vari
resistori.
1
Con gli indici 1_2, 3_4 sono indicate le resistenze equivalenti ai raggruppamenti in parallelo e con l’indice
1_2_3_4 la resistenza equivalente totale.
Ed ancora:
R resistenza misurata in ohm ();
I intensità di corrente misurata in ampere (A);
V tensione misurata in volt (V);
P potenza misurata in watt (W).
Procediamo passando dallo schema in Figura 1 a quello in Figura 2.
Figura 2
Ai raggruppamenti in parallelo sono state sostituite le resistenze equivalenti calcolate secondo la formula:
1
1
1
=
+
𝑅
𝑅1 𝑅2
I valori calcolati sono riportati in Figura 2.
Si passa, infine, dallo schema in Figura 2 a quello riportato in Figura 3, dove al raggruppamento in serie
della R1_2 con la R2_3 è stata sostituita la resistenza equivalente complessiva dell’intero raggruppamento
R = R1_2_3_4.
2
Figura 3
Si ricorda che la resistenza equivalente, in un raggruppamento in serie, è dato dalla formula:
𝑅 = 𝑅1 + 𝑅2
Aggiungiamo i valori trovati alla nostra tabella.
I valori di I complessivo (valore segnato dall’amperometro) e della potenza P complessiva sono stati ricavati
dalle formule:
𝐼=
𝑉
𝑅
e
𝑃 = 𝑅 ∙ 𝐼2
Ritornando dallo schema in Figura 3 a quello in Figura 2 abbiamo che la corrente che attraversa le due
resistenze in serie è la stessa di quella complessiva. Possiamo quindi determinare le due tensioni ai capi
delle resistenze (caduta di potenziale) tramite la formula:
𝑉 =𝑅∙𝐼
La tabella può essere quindi arricchita dei valori:
3
Nella tabella, le celle che contengono lo stesso valore sono distinte dallo stesso colore di fondo.
Nel raggruppamento in parallelo la tensione ai capi di ciascuna resistenza è uguale a quella della resistenza
equivalente, pertanto:
Procediamo quindi col calcolo a completare la tabella.
Si osservi che, a meno di errori di arrotondamento, la somma delle potenze dissipate da ogni singola
resistenza è uguale alla potenza dissipata dalla resistenza equivalente all’intero raggruppamento.
Prof. Ettore Limoli
4