NUMERI PRIMI CONGRUENTI
A 1 MODULO 4 E TEST DI PRIMALITA’
(PRIME NUMBERS CONGRUENT TO 1 MODULO 4 AND
PRIMALITY TEST)
Ing. Pier Francesco Roggero, Dott. Michele Nardelli, P.A. Francesco Di Noto
Abstract:
In this paper we focus our attention on a new primality test, based on
forms p = 4n+1 e p= 4n+3 of odd numbers of form 6n + 1, and if p or
p2 it is sum of two squares.
There are besides some thoughts on Fermat's theorem on sums of two
squares that states that every prime number can be written as the sum
of two perfect squares.
Versione 1.0
10/12/2013
Pagina 2 di 19
Riassunto
In questo lavoro focalizziamo l’attenzione su un nuovo test di primalità
basato sulle forme p = 4n + 1 e p = 4n +3 dei numeri dispari di forma
6k + 1 , e se p o p2 sono somma di due quadrati.
Questo tenendo conto del teorema di Fermat sulla somma di due
quadrati perfetti.
Versione 1.0
10/12/2013
Pagina 3 di 19
Index:
1. TRAPPOLE PER NUMERI PRIMI .................................................................................................... 4
2. TEOREMA DI FERMAT SULLE SOMME DI DUE QUADRATI .................................................. 7
3. ALTRI PROGRAMMI ...................................................................................................................... 15
4. RIFERIMENTI .................................................................................................................................. 19
Versione 1.0
10/12/2013
Pagina 4 di 19
1. TRAPPOLE PER NUMERI PRIMI
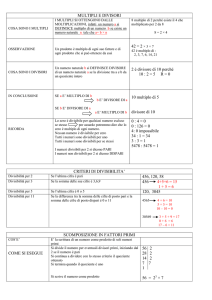
In questo lavoro riassumiamo in una Tabella, con qualche breve semplificazione,
il test di primalità del prof. Guido Carolla, vedi Rif. 1 e 2
Nel libro “PRIMI, PROGRESSIONI E MEDIE”, Casa ed. Kimerik, Il prof. Guido
Carolla ha mostrato un suo test di primalità, basato su alcune caratteristiche dei
numeri primi (forme 6n+1, 4n+1 come somma di due quadrati, 4n+3, ecc.) per
determinare con alta percentuale di sicurezza la loro primalità, e che
riassumeremo in una Tabella riepilogativa per facilitare il compito ad eventuali
lettori interessati.
TABELLA 1
6n + 1
N
4n +1 e
Esempi da
N^2
prof.
somma di
Carolla
(6n +1)/ 6 due
sempre
quadrati
intero
Se (4n-1)/
4 intero
989
Si, 165
Si , 247
No
solution
941
Si, 157
si, 235
si, 941^2
=580^2+
41^2
839
Si, 140
No
no solution
49
Si, 8
No
solution
4n+3
n’ n’’
(4n -3)
Se
(4n3)/4
3
intero
Primo
composto
Si
No
oppure
no
No
5*33
no
si
Si, 209
si
no
Composto
(quadrato, 7^2)
Versione 1.0
10/12/2013
Pagina 5 di 19
121
Si ,20
169 ecc
Si, 28
221
eccezione.
Si, 37
289 eccez
Si, 42
47
Si, 8
65437
Si, 10906
157
Si, 26
817
Si, 136
127
Si, 21
1861
Si, 310
1321
Si, 220
17129
Si, 2855
131
Si, 22
Altri
nostri
esempi
e
Si, 30
no
solution,
no
si, 42,
si solution
si, 55
si solution
si 72
si solution
no
no solution
si, 16359
si solution
si, 39
si solution
si, 204
no solution
no,
no
solution
si, 465
si solution
si, 330
si solution
si, 4282
no solution
si, 32
no
solution,
no
Composto
(quadrato, 11^2)
Si, 11
Composto(quadrato,
13^2)
No, 13 *17 anche se
la sequenza si, si no
lo dà per primo
No, quadrato
17^2
si
no
si
no
si
no
Si, 31
no
19*43
si
no
si
no
si
no
si
no
no
no
Versione 1.0
10/12/2013
Pagina 6 di 19
943
Si, 157
Si, 167
1001
…
…
no
si solution
si, 250
si solution
…
si, 235
no
no,
23*41
si
…
Il primo “Si” si può eliminare poichè (6n+1)/6 è sempre intero, quindi avremo,
più semplicemente, se si ottiene la sequenza:
si no solution,
si, si solution,
no, no solution,
si, no solution,
si, si solution
no si solution
si
no
si
no,
si
si
allora
allora
allora
allora
allora
allora
N = numero primo
N = numero primo
N = numero primo
N = numero composto
N = numero composto
N = numero composto
sono sei possibili sequenze sottolineate , tutte diverse tra loro: tre per i numeri
primi e tre per i numeri composti, con qualche rara eccezione, riguardante
quadrati, facilmente individuabili con l’estrazione della loro radice quadrata
(ovviamente se questa è intera, N è il suo quadrato). L’unica vera eccezione è 221 =
13*17, non quadrato, ma dato per primo dalla sequenza si si solution no.
Versione 1.0
10/12/2013
Pagina 7 di 19
2. TEOREMA DI FERMAT SULLE SOMME DI DUE QUADRATI
Il teorema di Fermat sulle somme di due quadrati afferma che ogni numero primo si
può scrivere come somma di due quadrati perfetti se e solo se è congruo a 1 modulo 4,
in altre parole se la differenza tra tale numero primo e 1 è multipla di 4.
p = x2 + y2 ,
p ≡1
(mod 4)
Per esempio:
5 = 12 + 2 2 , 13 = 2 2 + 3 2 , 17 = 12 + 4 2 ,
29 = 2 2 + 5 2 ,
37 = 12 + 6 2 ,
41 = 4 2 + 5 2 .
Fa eccezione il 2, che pur non essendo congruo a 1 modulo 4, può tuttavia essere scritto
come somma di due quadrati però uguali: 2 = 12 + 12 .
Si osservi che il numero primo p che si genera ha sempre come somma un multiplo
di 4 della forma (2n)2 con n = intero positivo ≥ 1
Quindi possiamo affermare che se un numero primo è dato dalla somma di 2
quadrati di cui un termine è un multiplo di 4 della forma (2n)2 con n ≥ 1 allora
sicuramente si ha anche che p≡1 (mod 4).
L’altro termine è di tipo (2m+1)2 con m intero positivo ≥ 0 e quindi è dato da tutti i
quadrati dispari, così la somma del termine pari della forma (2n)2 e di quello
dispari dà un numero dispari che è ovviamente primo.
Versione 1.0
10/12/2013
Pagina 8 di 19
Si ha:
per (2n)2 :
4, 16, 36, 64, 100, 144, 196, 256, 324, 400,…..
per (2m+1) 2 :
1, 9, 25, 49, 81, 121, 169, 225, 289, 361,….
Sommando un termine della 1° serie con uno della 2° serie si può ottenere un
numero primo p.
4+49 = 53
Ma ad esempio:
100+25 = 125 non è primo
Vediamo tutti i 10 casi che si presentano con le serie di numeri di sopra:
1+4=5
1+16=17
1+36=37
1+64=65 multiplo di 5
1+100=101
1+144=145 multiplo di 5
1+196=197
1+256=257
1+324=325 multiplo di 5
1+400=401
9+4=13
9+16=25 multiplo di 5
9+36=45 multiplo di 5
9+64=73
Versione 1.0
10/12/2013
Pagina 9 di 19
9+100=109
9+144=153 multiplo di 3
9+196=205 multiplo di 5
9+256=265 multiplo di 5
9+324=333 multiplo di 3
9+400=409
25+4=29
25+16=41
25+36=61
25+64=89
25+100=125 multiplo di 5
25+144=169 multiplo di 13
25+196=221 multiplo di 13
25+256=281
25+324=349
25+400=425 multiplo di 5
49+4=53
49+16=65 multiplo di 5
49+36=85 multiplo di 5
49+64=113
49+100=149
49+144=193
49+196=245 multiplo di 5
49+256=305 multiplo di 5
49+324=373
49+400=449
81+4=85 multiplo di 5
81+16=97
81+36=117 multiplo di 3 e di 13
81+64=145 multiplo di 5
81+100=181
Versione 1.0
10/12/2013
Pagina 10 di 19
81+144=225 multiplo di 5
81+196=277
81+256=337
81+324=405 multiplo di 5
81+400=481 multiplo di 13
121+4=125 multiplo di 5
121+16=137
121+36=157
121+64=185 multiplo di 5
121+100=221 multiplo di 13
121+144=265 multiplo di 5
121+196=317
121+256=377 multiplo di 13
121+324=445 multiplo di 5
121+400=521
169+4=173
169+16=185 multiplo di 5
169+36=205 multiplo di 5
169+64=233
169+100=269
169+144=313
169+196=365 multiplo di 5
169+256=425 multiplo di 5
169+324=493 multiplo di 17
169+400=569
Versione 1.0
10/12/2013
Pagina 11 di 19
225+4=229
225+16=241
225+36=261 multiplo di 3
225+64=289 multiplo di 17
225+100=325 multiplo di 5
225+144=369 multiplo di 3
225+196=421
225+256=481 multiplo di 13
225+324=549 multiplo di 3
225+400=625 multiplo di 5
289+4=293
289+16=305 multiplo di 5
289+36=325 multiplo di 5
289+64=353
289+100=389
289+144=433
289+196=485 multiplo di 5
289+256=545 multiplo di 5
289+324=613
289+400=689 multiplo di 13
361+4=365 multiplo di 5
361+16=377 multiplo di 13
361+36=397
361+64=425 multiplo di 5
361+100=461
361+144=505 multiplo di 5
361+196=557
361+256=617
361+324=685 multiplo di 5
361+400=761
Versione 1.0
10/12/2013
Pagina 12 di 19
Si generano moltissimi numeri primi, esattamente la metà ovvero il 50%.
Inoltre, notiamo che i numeri evidenziati in blu della 1° serie, sono tutti divisibili
per 8, che è un numero di Fibonacci ed è connesso ai “modi” corrispondenti alle
vibrazioni fisiche delle superstringhe attraverso la seguente equazione modulare di
Ramanujan:
∞ cos πtxw'
− πx 2 w '
∫0 cosh πx e dx 142
4 anti log
⋅ 2
πt 2
t w'
w'
−
e 4 φw' (itw')
1
8=
.
3
10 + 11 2
10 + 7 2
+
log
4
4
Osserviamo che:
I quadrati di numeri pari terminano sempre con le cifre:
0, 4, 6
I quadrati di numeri dispari terminano sempre con le cifre:
1, 5, 9
Sommando i quadrati di numeri pari con i quadrati di numeri dispari si ottengono
numeri dispari che terminano con le seguenti cifre:
1+0, 4, 6=1, 5, 7
5+0, 4, 6=5, 9, 1
9+0, 4, 6=9, 3, 5
E quindi possono terminare con tutte le cifre dispari 1, 3, 5, 7 e 9.
Vediamo in dettaglio:
1
di tutte le somme terminano con 5 e quindi non possono essere numeri primi.
3
1
di tutte le somme generano numeri composti.
6
Versione 1.0
10/12/2013
Pagina 13 di 19
1
1
di tutte le somme generano numeri primi, di questi terminano con le cifre 1,
2
6
1
1
1
terminano con le cifre 9,
terminano con le cifre 3 e
terminano con le
6
12
12
cifre 7
Versione 1.0
10/12/2013
Pagina 14 di 19
Abbiamo una distribuzione di numeri primi “REGOLARE” il che è molto strano e
inusuale, anzi sappiamo già a priori che con questo metodo si generano, ad
esempio, il 33,33% di numeri primi che terminano con la cifra 9 (considerando
solo i numeri primi che sono stati generati).
Interessante notare che nelle frazioni
1
1
ed , i denominatori 6 e 12 sono divisibili
6
12
per 24, numero connesso ai “modi” corrispondenti alle vibrazioni fisiche delle
stringhe bosoniche, attraverso la seguente equazione modulare di Ramanujan:
∞ cos πtxw'
− πx 2 w '
e
dx
∫
142
0 cosh πx
4 anti log
⋅ 2
πt 2
w'
−
t w'
4
(
)
e
φ
itw
'
w
'
.
24 =
10 + 11 2
10 + 7 2
+
log
4
4
Versione 1.0
10/12/2013
Pagina 15 di 19
3. ALTRI PROGRAMMI
Possiamo concludere che con questa semplificazione del Test di primalità del prof.
Guido Carolla abbiamo fatto un piccolo passo avanti verso una procedura più
semplice per testare un numero , con altissima percentuale di sicurezza, essendo
possibili rare eccezioni come 221, che pur essendo composto, passa tuttavia il test
come numero primo.
L’eseguibile per trovare rapidamente l’eventuale soluzione di N^2 è “ biquadrv”
biquadrvb.exe
, reperibile nel link
del prof. Giuseppe
,
http://matematicagratis.weebly.com/, insieme ad altri programmi :
Merlino:
ALTRI PROGRAMMI (DEDICATI SPECIFICATAMENTE ALLA TEORIA
DEI NUMERI), SI TROVANO QUI (NUMBER THEORY PROGRAMS IN
ENGLISH HERE):
http://numbertheorycalculator.myblog.it/
QUESTO E' L'INDICE DEI PROGRAMMI (QUASI TUTTI) :
ENGLISH INDEX AFTER ITALIAN INDEX
acamod.exe
aliquomio
amipevb
anadivi
anaprim
biquadrvb
biquagiu
carmivb
colivb
collamio
conichemio
contframio
aritmetica modulare
sequenze aliquot
n. amici e perfetti
numero e somma dei divisori. Abbondanti e deficienti.
analisi di un n. primo
N = x2 + y2 una soluzione
N = x2 + y2 tutte le soluzioni
numeri di Charmichael
a congruo a b mod c
Collatz
coniche
frazione continua di un radicale
Versione 1.0
10/12/2013
Pagina 16 di 19
cribuo
decbinmio
dessert
diffqua
dio1vb
diprevb
divimiovb
divrestvb
ducubvb
egimio
epeseg
eramio
evalmio
facred
factomio
fattomio
fibennevb
fifimio
formqmio
ge20vb
genfrape
gera2
gldb e gldb2
invmpvb
kquaku
mcdmpho
menoucon
minonrera
modpov
multffu
nepredi
nuprivb
palivb e pali2vb
pellvb
phivb
pidisp
pivbmio
n. primi tra a e b
da decimale a binario
deserti senza n. primi
a2 – b2
equazione diofantea di 1° grado
divisione 100 cifre
divisori
divisione con resto
a3 + b3 = c3 + d3
frazioni egiziane
N= a*b + a*c + b*c
crivello
valutatore espressioni numeriche
fattorizzatore
fattoriale cifre illimitate
fattori primi
e.mo n. di Fibonacci
numeri di Fibonacci
forme quadratiche
20 coppie di n. primi gemelli dopo N
frazione generatrice
fraz. generatrici di radical 2
congettura di Goldbach
inverso modulo p
a2 – b 3 = k
M.C.D e m.c.m.
x2 congruo a -1 mod. p
minimo non residuo quadratico e minima radice primitiva di p
ab modulo c (modpow)
varie di teoria dei numeri
divisione in multiprecisione
numero dei n. primi
serie palindromiche (reverse and add)
equazione di Pell
phi (funzione di Eulero)
pigreco da serie
pigreco cifre illimitate
Versione 1.0
10/12/2013
Pagina 17 di 19
pm7000
polipri
prienne
prifoda
prinextvb
quabicub
quanote
radimia
raprivb
renore
resnonres
segramio
siglimio
sistmio
sogevb
soquo
sosse
stinupri
studinterva
teiniz
tuttexp
tuttinve
tuttord
tvlvb
tepiprim
testprvb
tregrabuo e trgramio
trequavb
trequax
triavb
triquavb
tritarvb
tuquacu
unapit
unosup
variecost
vbmerse
crivello semplice
studio di x2 +x + 41
ennesimo primo
n. primi di forma data
nextprime
a2 = b 3 + c3
somme eguali di quadrati consecutivi
radice quadrata
tutte le radici primitive di p
residui e non residui quadratici di p
verifica se a è residuo o non residuo di p
secondo grado
singola linea del triangolo di Tartaglia-Pascal
sistemi di equazioni
numeri di Sophie Germain
12 + 22 + 32 + ....... N2
serie (1/(an))
stima del numero dei n. primi
studio di un intervallo
forme quadratiche
resti di aj modulo p
tutte le coppie di inversi di N
ordine di tutti gli a inferiori a p
N = x2 + y2 tavola
terne pitagoriche primitive
test di primalità
terzo grado
N = x2 + y2 + z2
P = x2 + y2 P2 = x2 + y2 P3 = x2 + y2
numeri triangolari
n. triangolari che sono quadrati esatti
triangolo di Tartaglia - Pascal
a2 – b 3 = k
singola terna pitagorica
periodo di 1/P
costanti varie
test di Lucas
Versione 1.0
10/12/2013
Pagina 18 di 19
vbpart
verordvb
zequcobvb
partizioni di N
ordine di a modulo p
z2 congruo a b modulo p
Versione 1.0
10/12/2013
Pagina 19 di 19
4. RIFERIMENTI
1) “TEOREMA SU UN TEST DI PRIMALITÀ CON FATTORIZZAZIONE
Guido Carolla
dal sito https://elvira.univr.it/bscwsci/pub/bscw.cgi/d3462092/n.174.pdf
2) libro di Guido Carolla “PRIMI, PROGRESSIONI E MEDIE”,
Casa ed. Kimerik
3) “ La congettura di Polignac”, parte finale dedicata alla fattorizzazione di prodotti
tra due numeri consecutivi
sul nostro sito
4) “La congettura percentuale”
sul nostro sito
5) ALTRI PROGRAMMI (DEDICATI SPECIFICATAMENTE ALLA TEORIA
DEI NUMERI), SI TROVANO QUI (NUMBER THEORY PROGRAMS IN
ENGLISH HERE):
http://numbertheorycalculator.myblog.it/