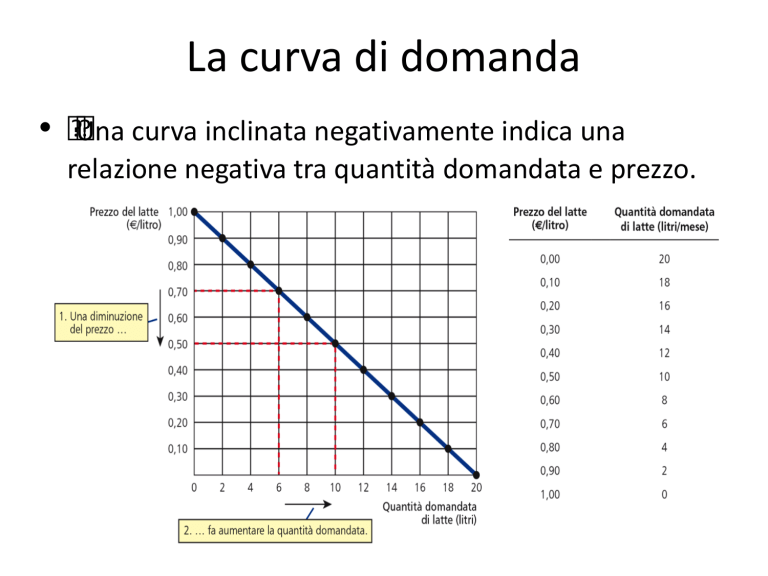
La curva di domanda
•
Una curva inclinata negativamente indica una
relazione negativa tra quantità domandata e prezzo.
La curva di domanda
•
Cosa accade se aumenta il numero dei il
numero dei consumatori?
• Cosa accade se aumenta il reddito dei
consumatori?
•Le curve di domanda definiscono le quantità domandate in
corrispondenza di ciascun prezzo.
•Esse sono costruite ipotizzando che solo il prezzo influenzi le decisioni
degli agenti o che, se intervengono altri fattori, questi ultimi siano
mantenuti costanti (ipotesi del ceteris paribus).
•Oltre che dal prezzo le decisioni di domanda possono essere
influenzate da:
• prezzo di altri beni
•Reddito
•preferenze dei consumatori
•Aspettative dei consumatori
•Pubblicità
•popolazione
Effetti del prezzo e di altri fattori sulla domanda
Movimento lungo la curva
L’OPEC aumenta il prezzo del
petrolio. Il prezzo della benzina
aumenta e la domanda
diminuisce
Spostamento della curva
La gente capisce che l’aria
pulita è importante. Il traffico
diminuisce e, con esso, la
domanda di benzina
L’ELASTICITA’
Elasticità della domanda
•Non è sufficiente sapere che la quantità
diminuisce o aumenta al variare del prezzo è
importante misurare anche di quanto varia
•l’elasticità misura la reattività della domanda
rispetto a variazioni del prezzo, ovvero in che
misura varia la quantità domandata al variare del
prezzo.
Elasticità della domanda
•L’elasticità dipende da:
•esistenza di buoni sostituti
• maggiore o minore importanza del bene per il
consumatore
• confini del mercato
•orizzonte temporale
Calcolare l’Elasticità
Prezzo
5
4
Domanda
La domanda è elastica
rispetto al prezzo
0
50
100
Quantità
9
elasticità= ΔQ/Q/ΔP/P
• Esempio: Se il prezzo di una bibita sale da
€4.00 a €5.00 e la quantità domandata passa
da 100 a 50, il coefficiente di elasticità sarà:
(50 - 100)
100
ED
(5,0 - 4,0)
4,0
- 50 %
2
25 %
La variazione assoluta
indicata dalla pendenza
della curva è data da
DQ/DP . Essa ci
fornisce qualche
informazione
sull’elasticità
approssimandola ma
l’elasticità è la
variazione
percentuale.
L’elasticità non è costante lungo una retta
Elasticità puntuale =
Dq/Q/Dp/P=
Dq/Dp/Q/P=
Dq/Dp x P/Q
Elasticità e variazioni della domanda
Se la domanda è rigida grandi variazioni del prezzo fanno variare
di poco la domanda
Se la domanda è elastica piccole variazioni del prezzo fanno
variare di molto la domanda
Elasticità/prezzo e ricavo totale
in una curva di domanda lineare
• In una curva di domanda anelastica rispetto al
prezzo, un aumento del prezzo determina una
riduzione meno che proporzionale della
quantità.
• Per cui il ricavo aumenta.
Come varia il ricavo totale quando cambia il prezzo:
domanda anelastica
P
P
Un aumento del
prezzo da €1
a €3 …
… porta
ad un
aumento del
ricavo totale da
€100 a €240
€3
Ricavo = €240
€1
D
Ricavo = €100
0
100
D
Q
0
80
Q
Price Elasticity and Total Revenue along a Linear
Curve è elastica, un aumento del
•Demand
Se la domanda
prezzo porta ad una riduzione più che
proporzionale della quantità domandata.
• Per cui il ricavo totale diminuisce.
Come varia il ricavo totale al variare del prezzo:
domanda elastica
P
P
Un aumento del
prezzo da €4
a €5 …
…porta
ad una
riduzione del
ricavo totale da
€200 a €100
€5
€4
D
D
Ricavo = €200
0
50
Ricavo = €100
Q
0
20
Q
Casi limite
IL PRODUTTORE
L’obiettivo dell’impresa
• L’impresa vuole massimizzare il profitto, il che
implica minimizzare i costi a parità di
produzione.
• Profitto= ricavo totale –costo totale
= RT -CT
= P · Q -CT
La funzione di produzione
Y = F(L)
Funzione di produzione
Y
YB
YA
B
•
•A
Insieme di
Produzione
L1
L
La funzione di produzione
È la relazione che intercorre tra la quantità
di fattori impiegata e la quantità di prodotto
ottenuta.
La funzione di produzione nel
breve periodo
Nel breve periodo solo il lavoro (L ) è variabile mentre il
capitale (K) è considerato fisso in quanto è realistico
pensare che se il produttore volesse ingrandire il proprio
stabilimento tale decisione richiederebbe un tempo
superiore all’anno (in altre parole: oltre il breve periodo)
K= FISSO
q= q(L)
La funzione di produzione nel
lungo periodo
Nel lungo periodo tutti gli input (nel nostro caso L e K)
sono variabili
q = q(L, K)
Prodotto totale e prodotto marginale
Se il prodotto totale Q dipende dal numero di
lavoratori impiegati appare fondamentale
comprendere di quanto fa aumentare il nostro
prodotto l’aggiunta di un lavoratore cioè conoscere
la produttività marginale di quell’ennesimo
lavoratore .
In formula PMG= ΔQ/ΔL
Produttività marginale
Pmg
w
N*
N
La Pmg indica di quanto cresce il prodotto totale
aggiungendo una unità di fattore produttivo – E’ decrescente
nel breve periodo in quanto il fattore capitale è fisso.
Funzione di produzione con due input
variabili
Se fissiamo il livello
produzione, q0, in
modo che
K
q0 = q(L, K)
è possibile rappresentare
la funzione di produzione
nel piano (L, K) attraverso
curve di livello dette
isoquanti
L
Isoquanto
È una curva su cui si trovano le combinazioni di
input che permettono di ottenere la stessa
quantità di output
La mappa degli isoquanti
A curve più lontane dall’origine
corrispondono livelli di
produzione maggiori (q2>q1>q0)
K
Gli isoquanti sono curve
decrescenti
q2
Gli isoquanti non si intersecano
tra loro
q1
q0
L
Il saggio (tecnico) marginale di
sostituzione
Ci dice di quanto deve aumentare la quantità
utilizzata di un input nel caso di una riduzione
unitaria della quantità utilizzata dell’altro
input se si vuole mantenere costante il livello
di produzione
è pari, in valore assoluto, al rapporto tra le
produttività marginali dei due input
I costi
Il costo totale nel caso di due input variabili (L e K) è
pari a:
CT = wL + rK
Dove w è il salario e r è il tasso di interesse
Se fissiamo il livello di costo CT0 è
possibile rappresentare il costo totale
nel piano (L,K)
K
CT0/r
w/r
Otteniamo la retta di isocosto
CT0/w L
La mappa degli isocosti
K
A rette più lontane
dall’origine
corrispondono
combinazioni dei due
input che comportano
un costo maggiore per
l’impresa
L
La combinazione ottima degli input
Dato il livello di produzione
fissato, q*, l’impresa sceglie la
combinazione dei fattori in
modo da minimizzare il costo di
produzione
La combinazione (L*, K*)
ottima corrisponde al punto di
tangenza tra isocosto e
isoquanto
K
E
K*
q*
L*
L
Nel punto di scelta ottima
PMGL
w
STS
PMGK
r
PMGL
PMGK
w
r
Il criterio di scelta della combinazione ottima degli input è dato
dall’uguaglianza delle produttività marginali ponderate (cioè
pesate per i prezzi degli input (salario e tasso di interesse)