Cinematica del moto rotatorio
Sino adesso ci siamo occupati del moto traslatorio di un corpo. In questo caso ciascun
punto del corpo si muove come tutti gli altri e quindi il moto di una singola particella,
il punto materiale, è rappresentativo del moto dell’intero corpo.
Adesso studieremo il moto rotatorio di un corpo. Cioè il caso in cui il corpo ruota attorno
ad un certo asse.
Per semplicità cominciamo a considerare il caso di un corpo rigido.
Cioè un corpo in cui le distanze relative fra tutti i punti sono costanti, anche quando il
corpo è soggetto a forze esterne.
In questo caso, potremo trascurare eventuali vibrazioni del corpo in questione.
1
Sia una particella che un corpo rigido in moto traslatorio si possono identificare univocamente
assegnando loro una posizione x,
y, z nel nostro sistema di riferimento.
Queste 3 coordinate tuttavia non sono sufficienti se il corpo rigido è anche soggetto ad un
moto rotatorio oltre che ad un moto traslatorio.
In generale, oltre alle tre coordinate
x, y, z che definiscono la posizione di un punto di
riferimento del corpo rigido, serviranno anche altre tre coordinate, tipicamente degli
angoli, che definiscono l’orientazione del corpo rispetto al sistema di riferimento.
2
Le figure di seguito illustrano la differenza fra moto semplicemente traslatorio e moto
traslatorio + rotatorio di un corpo rigido e la conseguente necessità di definire 6 coordinate
Moto traslatorio
y
x
3
Moto traslatorio + rotatorio
y
x
4
In questo caso, oltre che definire le coordinate x0-y0 del punto di riferimento 0 sul corpo,
rispetto al nostro sistema di riferimento, dovremo definire anche l’orientazione di un sistema
di assi x’-y’ solidale col corpo, rispetto al nostro sistema di riferimento x-y.
Moto traslatorio + rotatorio
y
0
y’
x
0
x’
0
5
Studieremo questo tipo di moto separando il moto traslatorio dal moto rotatorio.
Applicheremo in sostanza il principio di sovrapposizione.
Cioè: ad ogni istante lo stato del corpo è definibile in base ad una traslazione + una rotazione
6
Rotazione
Traslazione
y
x
7
Rotazione
Traslazione
y
x
8
Rotazione
Traslazione
y
x
9
Abbiamo già visto che per un sistema di particelle, rigido o non rigido, il centro
di massa (baricentro) si muove come se tutta la massa fosse concentrata in quel punto e
se tutte le forze esterne agissero su quel punto.
Cioè il moto del centro di massa di un corpo rigido è determinato dalla:
Fest = mtotale abaricentro
Questo moto è ovviamente solo traslatorio, essendo il baricentro un punto.
Quindi:
a) Il moto traslatorio di un corpo può essere descritto dal moto del suo baricentro
b) Il moto rotatorio sarà descritto dalla rotazione del corpo in questione rispetto ad un
determinato sistema di assi
10
Definizione formale di moto puramente traslatorio e di moto puramente rotatorio
Il moto di un corpo rigido è puramente traslatorio se tutti i punti del corpo
subiscono lo stesso spostamento in un dato intervallo di tempo
Il moto di un corpo rigido è puramente rotatorio se tutti i punti del corpo si muovono
su dei cerchi i cui centri sono localizzati tutti lungo una retta detta asse di rotazione
11
Se per ogni punto del corpo in questione, tracciamo dei segmenti perpendicolari
all’asse di rotazione, tutti questi segmenti ruoteranno di uno stesso angolo Δ θ in
un dato intervallo di tempo Δt
Δθ
Δθ
12
E questo va inteso anche nel caso 3D
13
E questo va inteso anche nel caso 3D
14
Per semplicità di trattazione, adesso prenderemo in considerazione il caso di un corpo
rigido che si estende solo in superfice, per esempio su un piano x-y e che ruota attorno
ad un punto 0, preso come origine del sistema di assi. In questo caso l’asse di rotazione è
l’asse z che interseca perpendicolarmente il piano x-y passando per 0.
y
O
x
z
15
Consideriamo un generico punto P e consideriamo il segmento
O-P.
Questo segmento è
fisso rispetto al corpo e ruota con esso. Ad ogni istante possiamo individuare la posizione
del corpo specificando l’angolo θ che il segmento O-P forma con l’asse x, che stabiliremo
positivo nel caso di rotazione in senso antiorario.
y
P
O
θ
x
θ θ (t)
z
16
Stabiliremo di misurare gli angoli in radianti. Un radiante è l’angolo al centro in un
cerchio sotteso da un arco di s lunghezza pari al raggio
R.
Pertanto un angolo θ è espresso in radianti dalla relazione
θ = s/R
1 rad
R
Poiché la circonferenza di un cerchio di raggio R è lunga 2πR, vi sono 2π radianti in
un angolo giro. Quindi 2π rad = 360°
1 rad ≈ 57,3 °
17
Supponiamo che il corpo rigido in questione ruoti in senso antiorario. Indichiamo
con θ1 l’angolo formato dal segmento O-P con l’asse x all’istante t1 e con θ2 l’angolo
al tempo t2.
Lo spostamento angolare nell’intervallo di tempo
Definiremo la velocità angolare media
Δt = t2 − t1
sarà
Δθ = θ2 − θ1
< ω > del corpo nell’intervallo Δt :
< ω > = (θ2 − θ1) / (t2 − t1 ) = Δθ / Δt
In perfetta analogia con quanto abbiamo studiato in cinematica nel caso lineare, la
velocità angolare istantanea sarà data dal limite per Δt
0 di questo rapporto:
ω(t) = lim Δθ / Δt = dθ /dt
Δt 0
18
La velocità angolare ha le dimensioni dell’inverso di un tempo:
[ T -1 ]
e in generale l’unità di misura è il
radiante / sec
19
Se la velocità angolare ω
(t) di un corpo non è costante, il corpo è soggetto ad una
accelerazione angolare. In analogia con quanto abbiamo già studiato, indicate con
ω1 e ω2
le velocità angolari agli istanti t1 e
t2
l’accelerazione angolare media
< α > è definita dalla relazione:
< α > = (ω2 − ω1) / (t2 − t1 ) = Δ ω / Δt
e di conseguenza l’accelerazione angolare istantanea è data dalla relazione
α (t) = lim Δ ω / Δt = d ω /dt
Δt 0
20
L’accelerazione angolare ha le dimensioni dell’inverso di un tempo quadrato:
[ T -2 ]
e in generale l’unità di misura è il
radiante / sec2
21
Analogia fra le grandezze cinematiche lineari e quelle angolari
Caso lineare
Caso rotazionale
x
[L]
θ
[]
v = dx /dt
[L T-1]
ω = dθ /dt
[T-1]
a = dv/dt = d2x/dt2
[L T-2]
α = dω/dt = d2θ/dt2
[T-2]
Le dimensioni lineari differiscono dalle corrispondenti dimensioni angolari
per un fattore avente dimensione di una lunghezza, il che deriva dalla definizione di
radiante
θ= s / R che è un numero puro, essendo il rapporto fra due lunghezze
22
Carattere vettoriale delle grandezze rotazionali
Avevamo visto che in cinematica lineare lo spostamento, la velocità e l’accelerazione
sono grandezze vettoriali, cioè necessitano anche della definizione di una direzione e di
un verso per essere individuate. Poi avevamo anche visto che nel caso unidimensionale
la trattazione era riconducibile al semplice caso scalare, in quanto la direzione è già
individuata, e il verso è specificato dal segno della grandezza scalare.
A prima vista sembra che anche le grandezze rotazionali siano dei vettori, in quanto
per ogni rotazione dobbiamo individuare l’asse di rotazione e il verso. E anche in questo
caso laddove esiste solo un asse preassegnato, possiamo trattare le grandezze in
questione come scalari.
Tuttavia, prima di affermare che le grandezze rotazionali sono dei vettori occorre
verificare che esse obbediscono alle regole del calcolo vettoriale,
in particolare le regole sulla addizione di vettori
23
Consideriamo il caso dello spostamento angolare θ
Si può verificare sperimentalmente che gli spostamenti angolari non si sommano come
vettori. Infatti se si sommassero come vettori dovrebbero obbedire alle regole sulla
somma dei vettori e in particolare alla proprietà commutativa della somma di due vettori,
cioè:
θ1 + θ2 = θ2 + θ1
24
Un libro ruota di 90° in senso orario
visto di fronte, e poi in senso antiorario
visto da sopra. Se l’ordine delle due
rotazioni viene invertito la posizione
finale è differente
Lo stesso succede se si adotta un
angolo di rotazione più piccolo, per
esempio di 45°, ma in questo caso
la differenza di orientazione finale
è minore
Nel caso di angoli sempre più
piccoli, la differenza di orientazione
finale tende a 0
25
Quindi:
θ1 + θ2 = θ2 + θ1
Ma:
dθ1 + dθ2 = dθ2 + dθ1
Gli spostamenti angolari infinitesimi obbediscono alla proprietà commutativa
dell’algebra vettoriale e infatti sono vettori
26
Di conseguenza, la velocità angolare:
ω(t) = dθ /dt
poiché dθ è un vettore e dt è uno scalare, ω è un vettore (e di conseguenza anche α)
Ma qual è la rappresentazione grafica di questo vettore? Consideriamo per esempio
Un cilindro che ruota attorno al proprio asse in senso antiorario:
ω
Il vettore velocità angolare ω è una freccia lungo la direzione dell’asse di rotazione,
orientata verso l’alto se la rotazione è in senso antiorario e viceversa se è in senso orario,
la cui lunghezza è pari al modulo ω.
27
La cosiddetta regola della mano destra.
Nozione mnemonica: se con la mano destra
si afferra idealmente l’asse di rotazione, in modo che le dita si avvolgano intorno ad esso nel
senso della rotazione, allora il pollice disteso punta nella direzione del vettore
ω
28
Notate che non c’è niente che si muove nella direzione del vettore ω
Il moto avviene nel piano ortogonale ad esso.
ω
29
Simboli comunemente usati:
Se consideriamo un moto rotatorio in due dimensioni, tale cioè che si sviluppi
per esempio sulla pagina del nostro quaderno:
•
Useremo il simbolo
๏ per il caso in cui il vettore emerge dalla pagina
Useremo il simbolo per il caso in cui il vettore punta verso la pagina
30
๏
31
Rotazione con accelerazione angolare costante
Il caso più semplice di un moto rotatorio è quello che avviene con accelerazione costante
In questo caso le equazioni del moto sono del tutto analoghe a quelle lineari (moto traslatorio):
Moto traslatorio
Moto rotatorio
v = v0 + a t
ω = ω0 + α t
x = ½ ( v0 + v ) t
θ = ½ ( ω0 + ω ) t
x = v0 t + ½ a t 2
θ = ω0 t + ½ α t 2
32
Il caso di una particella che si muove di moto circolare:
relazioni fra cinematica lineare e cinematica rotazionale
Abbiamo già studiato il caso di una particella che si muove di moto circolare,
e lo abbiamo fatto nell’ambito della cinematica lineare:
Quando un corpo rigido ruota attorno ad un asse fisso , tutti i suoi punti
compiono una traiettoria circolare. Quindi possiamo trattare il moto di tali
particelle sia usando variabili lineari che usando variabili rotazionali.
33
Consideriamo una particella situata nel punto P di un corpo rigido ad una distanza r
dall’asse di rotazione passante per il punto O. La particella in P si muove
lungo un cerchio di raggio
r mentre il corpo ruota
La particella percorre un arco di lunghezza
y
s mentre
il corpo ruota di un angolo θ e si ha:
s = rθ
P
O
r
θ
Se la posizione iniziale del punto P era lungo l’asse
lo spostamento risulta come indicato in verde
x
34
x
Derivando la reazione s
= rθ
rispetto al tempo e osservando che r è costante, si ha:
𝑑𝑠
𝑑𝜃
= 𝑟
𝑑𝑡
𝑑𝑡
Osserviamo che ds/dt è la velocità lineare v della particella nel punto
e
dθ/dt
è la velocità angolare
P
ω, e quindi risulta:
v= rω
Questa è una relazione fra i moduli dei vettori
ve ω
35
Data la relazione:
v= rω
Derivando rispetto al tempo e ricordando che r è costante, otteniamo:
𝑑v
𝑑ω
= 𝑟
𝑑𝑡
𝑑𝑡
Ma dv/dt è la componente tangenziale della accelerazione della particella (quella
che nel moto circolare uniforme risultava nulla) e
dω/dt
è il modulo della
accelerazione angolare del corpo rotante, quindi possiamo scrivere:
aT = rα
Abbiamo già visto a proposito del moto circolare che l’accelerazione centripeta (che
non è altro che l’accelerazione radiale) è invece data da
v2/r
Quindi
a R = v2/r
= ω2/r
36
Nel caso del moto circolare uniforme, che avevamo già studiato (adottando le grandezze
lineari e non ancora quelle rotazionali) risultava per definizione
aT = 0
Quindi: il moto di una particella lungo una traiettoria circolare si può descrivere sia
usando variabili lineari che usando variabili rotazionali
E poiché un corpo rigido è composto da N particelle, in linea di principio anche il
moto rotatorio delle N particelle di cui si compone un corpo rigido potrebbe essere
descritto da N variabili lineari.
Il problema è appunto che servirebbero N variabili, una per ogni punto, mentre
adottando le variabili rotazionali, queste sono le stesse per ogni punto
ECCO PERCHE’ ABBIAMO INTRODOTTO LE VARABILI ROTAZIONALI
37
Dinamica del moto rotatorio
Abbiamo visto che la relazione fondamentale di tutta la dinamica è la II Legge di Newton:
F = ma
Questa formulazione si è rivelata particolarmente utile per il trattamento della dinamica
delle particelle puntiformi e per il moto traslatorio di corpi, ma è chiaro che per il trattamento
del moto rotatorio dei corpi occorre riformulare questa legge usando variabili rotazionali.
Abbiamo già definito l’analogo rotazionale della accelerazione lineare a e cioè l’accelerazione
angolare
α = d ω /dt .
Dobbiamo adesso definire quali variabili rotazionali sono analoghe a F e
m
38
Consideriamo una barra disposta sul piano x-y e libera di ruotare attorno all’origine O.
Supporremo che il piano è orizzontale, così che non ci sia forza gravitazionale, e che
y
il piano sia privo di attrito:
O
F1
F1
x
Se applichiamo una forza F1 in un punto come in figura, la barra acquisirà una
certa accelerazione angolare
α1
Se però applichiamo la stessa forza F1 in un punto più distante dall’asse di rotazione,
come in figura, la barra acquisirà una certa accelerazione angolare maggiore
39
Questo è un fenomeno che ci è familiare in base ala nostra esperienza quotidiana:
Per aprire una porta facciamo meno fatica se spingiamo in un punto distante dall’asse
dall’asse di rotazione: è per questo che la maniglia è li e non vicino l’asse !
Se dovessimo aprire una porta applicando la forza ad un punto vicino l’asse, dovremmo
applicare una forza molto elevata, e se applicassimo la stessa forza lontano dall’asse, la
porta acquista maggiore accelerazione angolare !
Evidentemente ciò che conta per imprimere una accelerazione angolare non è solo la
forza
E vero che se aumentiamo la forza aumenta l’accelerazione angolare, ma possiamo
aumentare l’accelerazione angolare anche spostando il punto di applicazione della forza
40
Se invece applichiamo una forza F2 come in figura, cioè una forza la cui direzione passa
per l’asse di rotazione, non otterremo alcun moto rotatorio (e neanche traslatorio se la
barra è vincolata al suo asse)
y
O
F2
x
Evidentemente, oltre al punto di applicazione, anche la direzione della forza
è rilevante
nel determinare l’accelerazione angolare ?
41
Se adesso applichiamo una forza F3 come in figura, e scomponiamo la forza nelle sue
componenti
xey
ci renderemo conto che l’unica componente che conta è quella lungo
y
F3
O
x
Questo fatto conferma che, oltre al punto di applicazione, anche la direzione della forza
è rilevante
nel determinare l’accelerazione angolare
42
y
Occorre quindi identificare una grandezza fisica che rappresenti la causa della
accelerazione angolare, e che sia legata alla forza dalle proprietà che abbiamo
appena esaminato.
Questa grandezza sarà il cosiddetto momento della forza.
Ma prima di passare alla definizione del momento della forza, vediamo come
si comporta la massa, e vediamo se non sia necessario definire anche un’altra
grandezza analoga a ciò che è la massa nel caso lineare.
43
Supponiamo che la nostra barra sia costituita di due materiali di massa differente,
per esempio legno e ferro, e applichiamo la nostra forza F come in figura.
y
O
x
F
Otterremo una certa accelerazione angolare a
44
Se però capovolgiamo la barra e applichiamo la stessa forza
F
nel punto come in figura:
y
O
x
F
Otterremo una certa accelerazione angolare a maggiore !
E questo sebbene la massa della barra non sia cambiata!
E sebbene non sia cambiata la forza, né la sua distanza dall’asse di rotazione !!
Ciò che è cambiato è la distribuzione della massa rispetto all’asse di rotazione
45
Quindi: La grandezza analoga, nel moto rotazionale, alla massa nel caso traslatorio,
non è la massa ma una grandezza che potrebbe essere chiamata inerzia rotazionale e
che dipende in qualche modo dalla distribuzione della massa rispetto all’asse di rotazione
Cominciamo quindi a sviluppare in modo più rigoroso questi due concetti:
Momento di una forza
Inerzia rotazionale in funzione della distribuzione della massa
46
Momento di una forza
Definizione: Se una forza
F agisce su un punto P la cui posizione rispetto al riferimento
O è individuata da un vettore r,
il momento della forza rispetto a O è un vettore
definito dalla:
τ=rx F
dove il simbolo
x rappresenta il prodotto vettoriale fra r
e
F
Il modulo di τ è dato dalla relazione:
τ = r F sin θ
dove
θ
è l’angolo fra r e
F
La direzione è ortogonale al piano individuato da
la regola della mano destra
r e F, e il verso segue
47
48
Avevamo accennato durante le prime lezioni all’esistenza del cosiddetto
prodotto vettoriale fra due vettori, ma ci eravamo riservati di definirlo non
appena avessimo trovato una applicazione fisica che lo rendesse comprensibile.
Eccola !
Le dimensioni del momento della forza sono quelle di forza x distanza
E cioè [ M L T−2 L ] [ M L2 T−2 ]
L’unità di misura il nt-metro
49
Energia di rotazione e momento di inerzia
Non c’è dubbio che ciascuna particella di cui si compone un corpo rigido in rotazione
possiede un certa energia cinetica:
Una particella di massa m di un corpo rigido situata ad una distanza r dall’asse di
rotazione del corpo rigido in questione avrà una velocità
v = ω r , dove ω è la velocità angolare del corpo rigido.
ω
r
Pertanto l’energia cinetica di questa particella sarà:
½ m v2 = ½ m ω2r2
50
Se, come stiamo supponendo, il corpo è rigido allora la velocità angolare ω è la stessa
per tutte le particelle di cui si compone, e l’energia cinetica totale
K
sarà la somma delle energie cinetiche di tutte le particelle :
K = ½ m1 ω2 r21 + ½ m2 r22 + ………….. ½ mN ω2 r2N
+ m2 r22 + ………….. mN r2N ) ω2
K = ½ ( m1 r21
K= ½
∑(m r
Il termine
∑(m r
i
i
2
2
i
i
) ω2
) che indichiamo col simbolo I è denominato Momento di Inerzia
del corpo rigido rispetto a quel particolare asse di rotazione
I =
∑(m r
i
2
i
)
51
Va sottolineato che il Momento di Inerzia di un corpo rigido dipende quindi dall’asse,
oltre che dalla forma del corpo e dalla distribuzione delle masse.
Il Momento di Inerzia
I ha dimensioni:
[ M L2 ]
e si misura in:
kg m2
Introducendo il Momento di Inerzia, l’energia cinetica di un corpo rigido in rotazione
Krot
è espressa pertanto dalla:
Krot = ½ I ω2
52
Una interessante analogia:
Moto traslatorio
Moto rotatorio
Energia cinetica
½ m v2
½ I ω2
velocità
v
ω
massa
m
I
Cosi come ω è nel moto rotatorio l’equivalente della velocità v nel moto traslatorio,
I è nel moto rotatorio l’equivalente della massa m nel moto traslatorio.
Occorre però ricordare che mentre m non dipende dalla posizione del corpo, I dipende
dal particolare asse attorno a cui avviene la rotazione
53
Nota bene:
Questa non è una nuova forma di energia, ma è semplicemente la somma delle
energie cinetiche di tutte le particelle di cui si compone il corpo,
scritta semplicemente in una formulazione conveniente
54
Nel caso in cui il corpo rigido non è costituito da un insieme finito di particelle distinte,
ma è costituito da una distribuzione continua di materia, l’operazione di somma che
compare nella formula:
I =
∑(m r
i
2
i
)
diventerà una integrazione: considereremo il corpo costituito da masse infinitesime
dm e considereremo la distanza r
fra tali masse e l’asse di rotazione:
I =
∫
r2dm
dove l’integrale è esteso sull’intero corpo
55
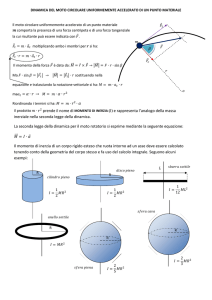
Nel caso di corpi di forma complicata, il
calcolo di questo integrale può essere
difficile, ma nel caso di corpi con una
geometria regolare e l’asse di rotazione
coincidente con l’asse di simmetria, il
calcolo è abbastanza semplice. Ecco di
seguito alcuni esempi:
56
Per la dinamica del moto rotatorio di un corpo rigido si definiranno pertanto una
serie di grandezze perfettamente analoghe a quelle del moto rettilineo di una particella :
Moto rettilineo di una particella
Moto rotatorio di un corpo rigido
Spostamento
x
Spostamento angolare
θ
Velocita
v = dx/dt
Velocità angolare
ω = dθ/dt
Accelerazione
a = dv /dt
Accelerazione angolare
α = dω/dt
Massa
m
Momento di inerzia
I
Forza
F = ma
Momento della forza
τ=Iα
Lavoro
∫ F dx
Lavoro
∫ τ dθ
Energia cinetica
½ m v2
Energia cinetica
½ I ω2
Quantità di moto
mv
Momento angolare
Iω
57
Momento angolare di una particella
Nella dinamica del moto rotatorio, il concetto di momento angolare (o momento
della quantità di moto) ha un ruolo simile a quello che ha la quantità di moto nella
dinamica del moto traslatorio. Vedremo che la definizione e l’applicazione di questo
concetto ci permetterà di ricavare un’altra importante Legge di conservazione.
Consideriamo una particella di massa m e quantità di moto p situata ad una distanza
r dall’origine O di un sistema di assi x-y-z.
Il momento angolare della particella
rispetto al punto O è definito dalla:
L = rxp
Cioè: il prodotto vettoriale di r per
p
58
L
y
p
r
y
z
59
In accordo con la definizione di prodotto vettoriale, il modulo di L è dato da:
L = r p sin θ
La direzione è perpendicolare al piano individuato dai due vettori r e p
Il verso è stabilito dalla consueta regola della mano destra.
Dalla definizione, che è del tutto analoga al momento di una forza, si vede che il
momento angolare
L è il momento della quantità di moto.
60
Adesso passeremo a dimostrare una importante relazione fra questi due momenti,
cioè il momento di una forza e il momento della quantità di moto.
Partiamo dalla II Legge di Newton, scritta nella sua forma più generale:
𝑑(𝑚𝒗)
F=
𝑑𝑡
e consideriamo il prodotto vettoriale di
r per entrambi i membri e cioè:
𝑑(𝑚𝒗)
rxF =rx
𝑑𝑡
che in base alla definizione di momento di una forza diventa:
𝑑(𝑚𝒗)
τ =rx
𝑑𝑡
61
Conserviamo per il momento questa relazione
definizione del momento angolare:
𝑑(𝑚𝒗)
τ =rx
𝑑𝑡
L = rxp
e torniamo alla
e deriviamo questa equazione rispetto al
tempo
𝑑𝐋
𝑑𝑡
=
𝑑
(r x p )
𝑑𝑡
La derivata di un prodotto vettoriale si esegue esattamente con le stesse regole di un
prodotto normale, fatto salvo il fatto che occorre fare attenzione a non invertire l’ordine dei
fattori.
62
Quindi si ha:
𝑑𝐋
𝑑𝑡
=
𝑑
𝑑𝒓
𝑑𝒑
(r x p ) = (
x p ) + (rx
)
𝑑𝑡
𝑑𝑡
𝑑𝑡
Notiamo che dr/dt altro non è che la velocità istantanea v della particella in questione.
Quindi potremo scrivere:
𝑑𝐋
𝑑
= (v x mv ) + ( r x
mv )
𝑑𝑡
𝑑𝑡
ma poiché il prodotto vettoriale di due vettori paralleli risulta nullo, v
x mv = 0
Si ha quindi:
𝑑𝐋
𝑑
= (rx
mv )
𝑑𝑡
𝑑𝑡
63
Confrontando questa equazione
𝑑𝐋
𝑑
= (rx
mv )
𝑑𝑡
𝑑𝑡
con quella che avevamo scritto per il momento della forza
𝑑
τ = (rx
mv )
𝑑𝑡
risulta:
𝑑𝐋
τ =
𝑑𝑡
Cioè: la derivata rispetto al tempo del momento angolare (o momento della quantità di
moto) di particella è uguale al momento delle forze applicate alla particella stessa.
64
Questa equazione:
𝑑𝐋
τ =
𝑑𝑡
è analoga alla equazione che avevamo scritto per il moto traslatorio:
𝑑𝐩
F=
𝑑𝑡
che stabiliva che la derivata rispetto al tempo della quantità di moto di una particella
è uguale alla forza che agisce su di essa, e che stabiliva, e che a implicava che:
dp = F dt Δp =
∫
F(t) dt
(relazione impulso – variazione quantità di moto)
Ci aspettiamo pertanto che risulti anche che:
dL = τ dt ΔL =
∫
τ(t) dt
65
Momento angolare di un sistema di particelle
Il caso trattato riguarda una particella. Nel caso di un sistema di più particelle,
dovremo tenere in conto la somma vettoriale di tutti i momenti angolari di ogni particella
rispetto allo stesso punto di riferimento O .
A variare del tempo, a secondo delle forze (o meglio dei loro momenti) agenti sul sistema,
potrà essere osservata una variazione
dL/dt.
In linea di principio, questa variazione
potrebbe essere imputabile a due cause:
a) Vi sono momenti di forze interne al sistema di particelle
b) Vi sono momenti di forze esterne al sistema di particella
Tuttavia, in base alla III legge di Newton, le forze fra coppie di particelle, non solo sono
eguali e contrarie, ma sono dirette lungo la linea che unisce le particelle e pertanto il
momento risultante è nullo.
66
Possiamo pertanto affermare che:
τest
𝑑𝐋
=
𝑑𝑡
E cioè: la rapidità con cui varia il momento angolare rispetto ad un dato punto è
uguale alla somma dei momenti delle forze esterne che agiscono sul sistema.
Poiché un corpo rigido è un particolare caso di un sistema di particelle (nel caso
specifico le distanze relative delle particelle sono fisse), la relazione dovrà valere
anche per il caso di un corpo rigido.
Avevamo già visto che in un corpo rigido risulta:
τest = I α
dove τ è il momento risultante delle forze esterne, I è il momento di inerzia del
corpo e α è la sua accelerazione angolare.
67
Confrontando la
τest
con la
𝑑𝐋
=
𝑑𝑡
τest = I α
risulta:
𝑑𝐋
=Iα
𝑑𝑡
𝑑𝐋
𝑑𝝎
=I
𝑑𝑡
𝑑𝑡
nel caso in cui I
= costante questa può essere scritta:
𝑑𝐋
𝑑
=
Iω
𝑑𝑡 𝑑𝑡
e cioè:
L=Iω
68
E cioè: il momento angolare di un corpo rigido è il prodotto del suo momento di inerzia
per la sua velocità angolare.
Si noti l’analogia della formula:
L= Iω
con la formula relativa al moto traslatorio:
p=mv
Risulta quindi
𝑑
τ=
Iω
𝑑𝑡
Se I = costante risulta
τ= Iα
69
Quindi, come in dinamica traslatoria si ha
F=ma
In dinamica rotatoria si ha
τ= Iα
E così come la F
=ma
poteva essere formulata nel caso più generale caso di
una massa variabile con la formula:
𝑑
𝑑
F=
(m v) =
p
𝑑𝑡
𝑑𝑡
Per il momento angolare avremo in generale:
𝑑
𝑑
τ=
(Iω) =
L
𝑑𝑡
𝑑𝑡
70
Conservazione del momento angolare
Dalla relazione precedente risulta che se :
τest
𝑑
=0
L=0
𝑑𝑡
Cioè: quando il momento risultate delle forze applicate ad un sistema è nullo, il
momento angolare è costante.
Cioè: il momento angolare di un sistema isolato è costante
QUINDI: in un sistema isolato
I ω = costante
71
Se durante il moto rotatorio cambia la distribuzione delle masse (e quindi cambia I)
cambierà di conseguenza
ω, un fenomeno largamente usato da atleti
e ballerini !!!
72