Il prodotto ∙ 2 prende il nome di MOMENTO DI INERZIA ( ) e

DINAMICA DEL MOTO CIRCOLARE UNIFORMEMENTE ACCELERATO DI UN PUNTO MATERIALE
Il moto circolare uniformemente accelerato di un punto materiale
comporta la presenza di una forza centripeta e di una forza tangenziale
la cui risultante può essere indicata con ⃗ .
⃗
⃗ =
⃗
∙ ⃗ moltiplicando ambo i membri per si ha:
⃗ ∙ =
∙⃗ ∙
⃗
Il momento della forza ⃗ è dato da: ⃗ = ⃗ × ⃗ →
Ma
= ⃗
∙ sin
⃗ =
⃗ = ⃗ ∙ sostituendo nella
→
equazione e tralasciando la notazione vettoriale si ha:
ma
=
∙
→
∙ ∙ sin
=
∙
Riordinando i termini si ha:
=
∙
∙
∙
=
∙
2
∙
2
prende il nome di MOMENTO DI INERZIA ( ) e rappresenta l’analogo della massa
inerziale nella seconda legge della dinamica.
Il prodotto
∙
La seconda legge della dinamica per il moto rotatorio si esprime mediante la seguente equazione:
⃗= ∙ ⃗
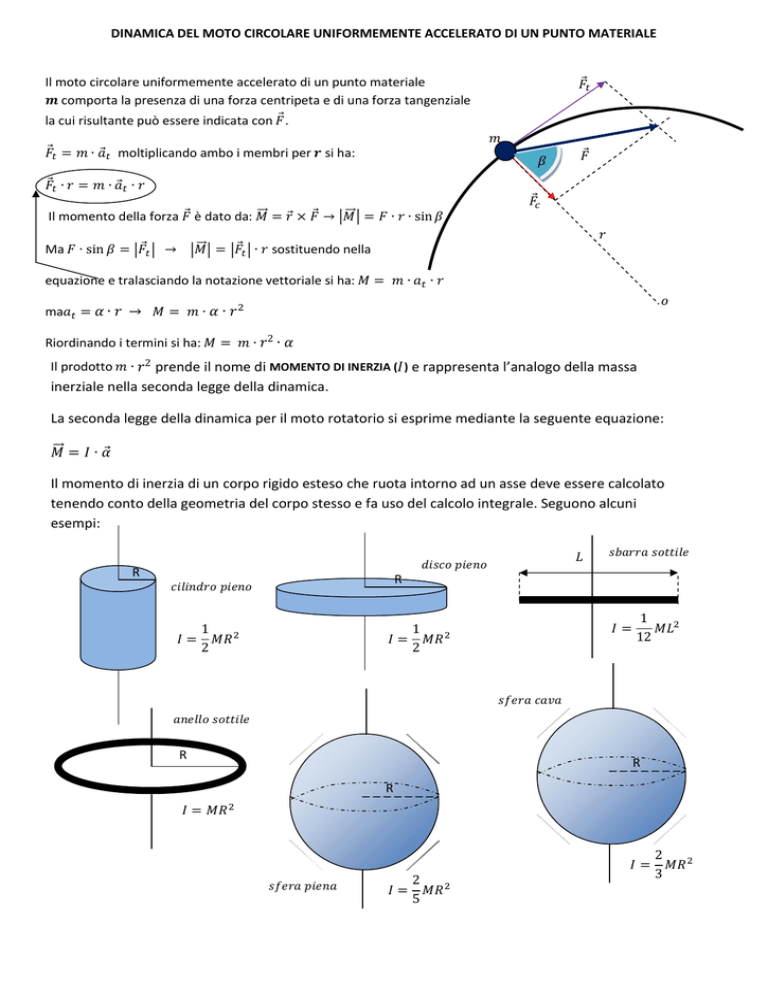
Il momento di inerzia di un corpo rigido esteso che ruota intorno ad un asse deve essere calcolato
tenendo conto della geometria del corpo stesso e fa uso del calcolo integrale. Seguono alcuni
esempi:
R
R
1
=
2
1
=
2
R
=
1
12
R
R
=
=
=
2
5
2
3
La tabella che segue mostra le analogie tra il moto traslatorio e il moto rotatorio.
MOTO TRASLATORIO
MOTO ROTATORIO
⃗=
⃗=
=
⃗=
⃗=
⃗=
⃗=
⃗=
à
⃗=
⃗=
à
à
∆ =
∆ =
=
=
=
−
=
⃗=
⃗= ⃗
∙⃗
Se ⃗ = 0  ⃗ = 0 m.rett.u. ⃗ =
.
∆ = ∆
. ⃗ =
. m.r.u.a.
Se ⃗ =
= + ∆ ∆ = ∆ + ∆
⃗=
⃗ = 0 m.rot.u. ⃗ =
Se
⃗=
Se
=
.
= 0∆⃗ = 0 ⃗ =
= ∆
1
=
2
=∆
. ∆ =
. ⃗ =
+ ∆ ∆ =
⃗=
⃗
⃗∆ = ∆ ⃗
Se ⃗
à
∆
. m.rot.u.a.
∆ + ∆
⃗
⃗∆ = ∆ ⃗
.
Se
⃗
.
= 0  ∆⃗ = 0  ⃗ =
=
1
2
=∆
=
∆
.