LE FRAZIONI EQUIVALENTI
ISTITUTO COMPRENSIVO “GABELLI” PLESSO ALDO
MORO
II D-II E
DOCENTE: SIBILLANO GIUSY
DEFINIZIONE
Due o più frazioni si dicono equivalenti se, pur essendo rappresentate in modo
diverso,
• Rappresentano:
la stessa quantità minore di un intero (se le frazioni sono proprie);
la stessa quantità congruente o multipla di un intero (se le frazioni sono
improprie apparenti);
la stessa quantità maggiore dell’intero (se le frazioni sono improprie non
apparenti);
• Rappresentano lo stesso numero:
decimale limitato o illimitato periodico minore di 1 (se le frazioni sono
proprie);
naturale (se le frazioni sono improprie apparenti);
decimale limitato o illimitato periodico maggiore di 1 (se le frazioni sono
improprie non apparenti);
ESEMPI:
DATA UNA FRAZIONE, QUANTE FRAZIONI
EQUIVALENTI AD ESSA ESISTONO?
• Le frazioni equivalenti ad una frazione data
sono infinite, per cui, si sceglie una frazione
con numeratore e denominatore primi tra loro
(detta frazione ridotta ai minimi termini) come
rappresentante di una classe di equivalenza.
Esempio:
COME TROVARE LE INFINITE FRAZIONI
EQUIVALENTI?
Basta applicare la:
PROPRIETA’ INVARIANTIVA:
Data una frazione, basta moltiplicare o dividere
numeratore e denominatore per uno stesso
numero diverso da 0 per ottenere infinite
frazioni equivalenti a quella data.
LA PROPRIETA’ INVARIANTIVA
SECONDO VOI E’ PRECISA LA DEFINIZIONE DI
SCORSA VOLTA?
DELLA
La risposta è no.
Usando quella definizione , cioè
,inseriremmo infiniti numeri con lo stesso valore
Esempio:
=
Ciò non avrebbe senso!...perchè ripetere numeri
con lo stesso valore?!
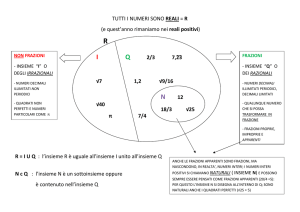
NUOVA DEFINIZIONE DI
E SI LEGGE:
INSIEME DELLE CLASSI DI EQUIVALENZA I CUI RAPPRESENTANTI SONO FRAZIONI CON
NUMERATORE (NUMERO NATURALE) E DENOMINATORE (NUMERO NATURALE
DIVERSO DA 0) PRIMI TRA LORO .