Capitolo_6_Correnti

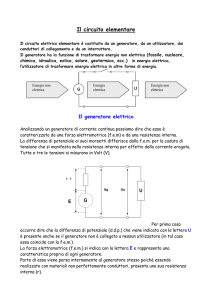
Conduzione elettrica
C1 + +
+
t=0
+
+ V1
+
+ +
C2 - V2
- - -
Nel filo a t = 0:
+ fluisce C1  C2 ;
- fluisce C2  C1
 Corrente elettrica I(t) rapidamente I(t*)= 0
V2 (t*)  V1 (t*)
t*<< 1 s
Chi provoca moto delle cariche nel filo?
nel filo: campo E  V2 (0)  V1 (0) 
 E  dl
 filo
V2 (t*)V1(t*)  0 Efilo(t*)  0
C1 + +
+
+
V1
+
+ I(t)
+
+
C2 - V2
- -
Come mantenere I costante??
Occorre : V2 (t) V1(t) 
E
filo
(t)  dl = costante
 filo
 E filo  costante
Occorre “forza esterna” che continuamente
ritrasferisca: cariche +e C2  C1
cariche -e C1  C2
in modo che:
V2 - V1  d.d.p. = costante
il lavoro per unità di carica fatto da
questa forza esterna è chiamato:
forza elettromotrice (f.e.m.) ?
“Forza” elettromotrice (f.e.m.): sorgente di
energia per mantenere le cariche in moto
Analogia gravitaz.
f=F/m
g
DV=DU/m=gh
g
g
x mantenere sciatori in circolo  sciovia
durante percorso ciclico dello sciatore:
Lf   f  dl  f h = gh
energia (per unità di massa) necessaria per
riportare su lo sciatore (Lf contro forza peso)
g conservativa  Lg  g  dl  0

“Forza” elettromotrice (f.e.m.): sorgente di
energia per mantenere le cariche in moto
quindi I costante
Fine XVIII secolo: cella di Volta
I costante
+
Cu

ddp = o costante
-
Acqua + NaCl Zn
Cariche –e che fluivano nel filo da Zn a Cu
continuamente ripristinate da reazione chimica
 o è la forza elettromotrice (f.e.m.)
Cella di Volta: primo generatore f.e.m.
oggi anche altri generatori f.e.m.:
• celle fotovoltaiche
• dinamo, alternatore, ecc.
• pile a combustibile
• meccanici, ecc..
Corrente elettrica
S
q
v
S’
^
n
q
dS
Definiamo Intensità di corrente elettrica:
IS
dq

dt
la carica che fluisce nell’unità di tempo attraverso
una qualsiasi S del conduttore
U.M.  Ampere (1 A  1 C/s)
S1
I1
S2
I2
Densità di Corrente elettrica
dS
S
J
Vettore J densità di corrente: corrente
attraverso superficie unitaria S’ ^ a v
J || v (A/m2)  I  J  ^
n dS
S

S
A
N v
dl
I  Nvq  n  Adl  v  q

J  nvq
Corrente elettrica
Dalle definizioni, per una superficie chiusa
Schiusa segue:
I Schiusa 
 J  nˆ dS  
Schiusa
dq


   dV    dV
dt
t V
t
V
dal teorema della divergenza:
Φ S ( chiusa ) ( J ) 
 J  nˆ dS
S ( chiusa )
segue:
ovvero:
    J dV
V

J  
t

J 
0
t
equazione di continuità della corrente elettrica
Correnti stazionarie
Stazionarietà: IS1 = IS2
ovvero:   0
t
S’ chiusa
S1
q
v
S2
(I  continua se costante nel tempo)
Conseguenze stazionarietà della corrente:
   J  0 linee di J sono chiuse

ρ
 0  ρ( filo)  costante
t
stessa condizione dell’elettrostatica
 campo elettrico nel filo è conservativo
Conduttore filiforme
d.d.p.V
A
l
I = V/ R
R = R l/A
1° legge di Ohm (solidi)
R resistenza elettrica – ohm (Ù)
2° legge di Ohm
R resistività elettrica (Ù m)
Conduttori
10-8<  R < 10-5 (metalli)
Semiconduttori 10-1<  R < 103 (Si, Ge puri)
Isolanti
107<  R < 1017( vetri, ceram.)
Metalli:  R (T)=  Ro(1+aT): aumenta con T
Semiconduttori puri: diminuisce con T
A
Rappresentazione grafica di R
I
VAB= I R
B
R
Casi più “complicati“: resistenze in serie
I
A
B
C
R1
R2
I= I1 = I2
A
VAB= VAC + VCB = IR1+IR2
Situazione “equivalente“
I
Req= ?
B
Req
VAB= IReq = I (R1+R2)
 Req = R1+R2
Rserie = R1+R2+….Rn Predomina la + grande
I
Resistenze in parallelo
I1
R1
I
B
A
I2
R2
VAB= I1R1=I2R2
I= I1 + I2 1° Legge di Kirchoff (x 1 nodo)
A
Situazione “equivalente“
I
B
VAB =IReq
Req
I= I1 + I2 = VAB / R1+ VAB / R2
I = VAB / Req=VAB ( 1/ R1+1/ R2 )
 1/ Req=1/ R1+1/ R2
1/Rparallelo =1/ R1+1/ R2+….1/ Rn
Predomina la + piccola
R1  R2
Req 
R1  R2
1° Legge di Kirchoff
Definita una superficie chiusa che attraversi un
circuito elettrico, la somma algebrica delle
correnti che attraversano la superficie (con segno
diverso se entranti o uscenti) è ad ogni istante
nulla:
 ik (t )  0

In una formulazione semplificata, in ogni nodo
di un circuito elettrico la somma delle correnti
entranti è uguale alla somma delle correnti
uscenti:
Ie1
Iu1
Ie2
Iu2
 Ie   Iu
Bilancio energetico
I
A
B
VAB= I R
R
la resistenza si scalda
l’ energia fornita dal generatore si dissipa
in calore
Resistenza elettrica: rappresenta effetto
dei processi dissipativi microscopici (urti
elettroni- ioni ) equivalenti a forza di
attrito macroscopica
Conduttore filiforme
d.d.p.V
E
I
resistenza R
Durante dt il campo E fa fluire dq=I dt
il lavoro eseguito da E (generatore) è:
dLgen = V dq= V I dt
Wgen = dLgen/dt = V I
2
V
Wgen  VI  I R 
R
2
effetto Joule
“Forza” elettromotrice (f.e.m.): sorgente
di energia x mantenere cariche in moto
Analogia
f=F/m
g
DV=DU/m=gh
g
g
x mantenere sciatori in circolo  sciovia
durante percorso ciclico dello sciatore:
Lf   f  dl  f h = gh
energia (a unità di massa) necessaria per
riportare su lo sciatore (Lf contro forza peso)
g conservativa  Lg  g  dl  0

“Forza” elettromotrice
(f.e.m.) e circuiti elettrici
Es
d.d.p. = o
E
s
+
A
+
Eem
Es +
+
I
Es
R
(cost.)
-- B
-Es
Es
Es
per mantenere la carica costante sugli elettrodi
occorre un campo (Eem) che faccia lavoro contro
Es per riportare le cariche“indietro”
Generatori di f.e.m.: pila , dinamo,
celle fotovoltaiche, ecc.
“Forza” elettromotrice
(f.e.m.) e circuiti elettrici

d.d.p. = o
+ -
(cost.)
I
I
I
I
I
A
R
I
B
In un generatori di f.e.m. “ideale”:

VA – VB  VR = o  I  o
R
IR = VR =
dq dL
W  I o 

dt dq
o
potenza erogata dal
generatore
“Forza” elettromotrice
(f.e.m.) e circuiti elettrici

d.d.p. = o
+ -
(cost.)
I
I
I
I
A
R2 B
R1
In un generatori di f.e.m. “ideale”:

V A  V B  V R1  V R 2  IR1  IR 2  o
2°Legge di Kirchoff (x 1 maglia)
I
o
R1  R2
2° Legge di Kirchoff
In ogni maglia di un circuito la somma algebrica
delle tensioni (con il segno appropriato in funzione
del verso di percorrenza della maglia stessa) è pari
a zero.
 Vi  0
Generatori di f.e.m. reali
In realtà, in un generatore reale:
o
+
Ri
-
resistenza interna
I
R
I 
VRi
o
VR
da cui:
R  Ri

Ri
o
 IR 
i
“caduta di potenziale”
su Ri
R  Ri
VR  IR 
o R
R  Ri

o
1  Ri / R

o
Generatori di f.e.m. reali
I gen. f.e.m. dissipano energia internamente
+
o
-
Ri
schematizza:
dLint/dt = I2Ri
I
R
Ri resistenza
interna generatore
Wgen = I o = I2 Ri + I2 R
(bilancio energetico)
o = I Ri+I R
2°Legge di Kirchoff (x 1 maglia)
VR= IR=
o - IRi  o
Misura della f.e.m. o
+
o -
Ri
schematizza:
dLint/dt = I2Ri
I
Ri resistenza
interna generatore
R
VR  IR 
o R
R  Ri

o
1  Ri / R

o
per misurare o occorre che R 
,
ovvero I = 0 ( misura a circuito aperto)
Esercizio 6.1
Un generatore ideale di f.e.m. = 12 V e è chiuso sul circuito rappresentato in
figura con i valori R1 = R2 = R3 = 10 W. Calcolare differenza di potenziale fra A e
B.
f.e.m.
R1
A
R2
R3
B
Esercizio 6.2
Un generatore di f.e.m. = 12 V e resistenza interna Ri = 0.2 W è chiuso sul
circuito rappresentato in figura con i valori R1 = R2 = R3 = 10 W. Calcolare la
potenza dissipata su R3.
f.e.m.
Ri
R1
R2
R3
Esercizio 6.3
Un generatore di f.e.m. E0 = 10 V e resistenza interna Ri = 10 W, è
collegato al sistema di tre resistenze, ognuna di valore R = 200 W
come in figura. Calcolare: a) la d.d.p. fra i punti A e B; b) la
potenza dissipata su R2 ; c) la potenza erogata dal generatore.
A
E0
Ri
R1
R2
R3
B
Scarica di un condensatore
C carico con qo
+
Chiudendo S: scorre I(t)
uguale in tutto il circuito
 I stazionaria
VR  VC

t
dq
dt
 
q
RC
q (0)

0
-
VC
S
R
qt
 ItR 
C
dq
ma: I  
dt
q (t )
I
C
VR
dqt
qt
 

dt
RC
 q(t) 
t
t
 ln   

RC
τ
 qo 

 q(t)  q o e
t
τ
τ  RC
τt
q(t)  q o e
con: τ  RC
t
qo  τ
e
dq
I (t) 

dt
τ

I(t)  Io e

t
τ
t
qo  τ
e
RC
t
Vo  τ
e

R
Vo
con: Io 
R

qo
VR (t)  IR 
e
C
t
τ

 VC (t)  Voe
q,I VR ,VC
V0 , I0 , q0
e

t
τ
@ 37%
t
t
t
τ

q(t)  q o e
t
τ
I (t )  Ioe

t
τ
q,I,
e

t
τ
t
Energia totalmente dissipata in R:

U 
 I (t )
o

2
Rdt 

o
2  2t
Vo
e τ dt
R
1

RCVo2 
2R
1
 CVo2 = energia iniziale in C
2

q(t)  q o e
t
τ
I (t )  Ioe

t
τ
q,I,
e

t
τ
t
Energia rimasta in C al tempo t*:

1
1 
2
U  CVC t *  C Vo
2
2 

t 2


τ
e


Carica di un condensatore
Chiudendo T:
scorre I(t)=dq/dt
Vo
C
T
R
q
Vo  VR  VC  VR  IR  Vo 
C
dq
q
R  Vo 
dt
C
q (t )

t

dq

(Vo C  q )
q (0)

0
t
τ
q(t) q f (1 e )
dq
1


(VoC  q)
dt
RC
dt
RC
 ln(
VoC  q(t )
t
) 
(VoC  q(0))
RC
dove: qf  VoC ; τ  RC
q(t)  q f (1  e
q(t)
VC(t) 

C
t

τ
)
t

Vo(1e τ )
t
Vo  τ
e

dq
I (t ) 

dt
R
VR (t)  IR  Voe
q,VC
I,VR

t
τ
(1e )
e
t

t
τ
t
τ
t
Ricapitolando:
Energia fornita generatore


2
o
V
U   Vo I (t ) dt  
e
R
o
o

t
τ
dt  CV
2
o
Energia accumulata in C
U
C
2
q
1 f
1

 CV
2 C
2
2
o
Energia dissipata in R


2
o
V
U R   I (t ) Rdt  
e
R
o
o
2

2t
τ
1
dt  CVo2
2
Esercizio 6.4
Si consideri, nel circuito rappresentato in figura, la carica dei due
condensatori C1 = C2 = 20 μF ad opera del generatore con V0 = 10
V attraverso le due resistenze R1 = R2 = 400 kΩ. Si calcoli: a) la
costante di tempo τ del circuito; b) il valore di VAB(t*) e
dell’energia UC(t*) accumulata nel sistema dei due condensatori al
tempo t* = 4 s.
C2
C1
A
B
V0
R1
R2
Esercizio 6.5
Due condensatori di capacità C1 = 100 mF e C2 = 200mF sono
caricati separatamente a differenze di potenziale rispettivamente V1 =
10 V e V2 = 20 V. I condensatori vengono quindi staccati dai
generatori e collegati in parallelo fra di loro. Il sistema dei due
condensatori in parallelo viene poi fatto scaricare su una resistenza di
valore R = 100 KW. Calcolare la d.d.p. ai capi dei condensatori dopo
t* = 10 s dal collegamento con la resistenza.
C1
V1
C2
V2
Esercizio 6.6
Due condensatori rispettivamente di capacità C1 = 4 mF e C2 = 6 mF
sono inizialmente caricati separatamente alle tensioni V1 = 200 V e
V2 = 350 V. Vengono quindi connessi in parallelo come in figura
attraverso la resistenza R. Determinare: a) le tensioni finali V’1 e
V’2 e b) l’energia dissipata su R dopo un tempo infinito dal
collegamento in parallelo.
Esercizio 6.6
Un condensatore di capacità C = 100 mF viene caricato alla differenza di potenziale
V0 = 100 V e quindi fatto scaricare su una resistenza con valore R = 10 kΩ posta in
parallelo a una barretta fatta di materiale con resistività  = 10 Ωּm di sezione
uniforme S = 0.5 cm2 e lunga L = 10 cm. Si calcolino i valori dell’energia
elettrostatica accumulata nel condensatore al tempo t* = 2 s dopo l’inizio della
scarica.
C
R
