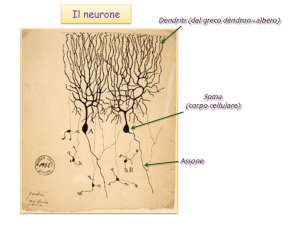
Genesi del Potenziale
di Membrana
In tutte le cellule è possibile misurare una
differenza di potenziale a cavallo del plasmalemma
Forze agenti sugli ioni
• Gradiente di Concentrazione
• Campo Elettrico
Energia chimica
Energia elettrica
è l’energia contenuta in un
gradiente di concentrazione
è l’energia dovuta alle cariche
in un campo elettrico
Cosa accade quando la membrana è permeabile solo ad uno ione?
nessuna differenza di potenziale
elettroneutralità
elettroneutralità
Cosa accade quando la membrana è permeabile solo ad uno ione?
un catione si muove dalla
zona ad alta a quella a
bassa concentrazione
nessuna differenza di potenziale
elettroneutralità
elettroneutralità
Cosa accade quando la membrana è permeabile solo ad uno ione?
Su entrambi i lati le
cariche non sono più
bilanciate
- voltaggio +
eccesso di carica -
eccesso di carica +
Cosa accade quando la membrana è permeabile solo ad uno ione?
l’eccesso di cariche + tende a
respingere i cationi da questo lato
- voltaggio +
eccesso di carica -
eccesso di carica +
Cosa accade quando la membrana è permeabile solo ad uno ione?
viene raggiunto un equilibrio:
la forza dovuta al gradiente di concentrazione
uguaglia
la forza dovuta al gradiente elettrico
- voltaggio +
eccesso di carica -
eccesso di carica +
GENESI DI UN
POTENZIALE D’EQUILIBRIO
0
++-
K+
Na+Cl100 mM
ΔE
K+
K+
K+
++++-
++-
K+Cl100 mM
ΔC
ΔE
++++-
ΔC
ΔE
K+
ΔC
All’equilibrio:
flusso dovuto al gradiente di conentrazione = flusso dovuto al potenziale elettrico
Il potenziale di equilibrio può essere
calcolato dall’Equazione di Nernst
[C ]1
RT
E
ln
zF
[C ]2
R= 8.3 J/mol oK =1.98 cal/mol oK (cost. dei gas)
T = 293 oK (20 oC)
z = +1 (per Na+, K+, H+ etc)
z = -1 (per Cl-)
E
z = +2 (per Ca2+ etc)
F = 96,500 coulomb (costante di Faraday)
1
-
+
+
+
+
K+
-
+
+
+
+
2
K+
[C ]1
58mV Log10
[C ]2
L’equazione di Nernst può essere ricavata in
base a considerazioni puramente teoriche
La variazione di energia libera ΔG, ovvero il lavoro W associati con il trasporto di uno ione
(i) attraverso la membrana possono essere scritti come:
[i ]est
G W Go RT ln
zFE
[i ] int
Dal momento che lo ione i è elettricamente carico, nel computo di ΔG (o di W) vi è sia una
componente chimica RTln([I]est/[I]int) che una componente elettrica zFE.
(Go è la variazione di energia libera standard, dovuta alla composizione molecolare;
notare che in questo caso ΔGo=0, non venendo rotti dei legami nè generato calore)
All’equilibrio ΔG (ovvero W) è zero e quindi:
zFE RT ln
[i ]est
[i ] int
Pertanto il potenziale di equilibrio dello ione i è:
Ei
RT [i ]est
ln
zF [i ] int
Notare che:
[i ]int [i ]est
zF
Ei
e RT
Ovvero, essendo:
qe=carica dell’elettrone=F/N
R=cost. dei gas=kBT
dove:
kB (cost. di Boltzmann)
N (numero di Avogadro: n. particelle/mole)
F (cost. di Faraday:carica di una mole di elettroni)
[i ]int [i ]est e
zq e
Ei
k BT
Distribuzione di Boltzmann
Un esempio pratico
una cellula
Supponendo che la membrana di una
cellula sia permeabile solo al K+,
calcolare il potenziale di membrana
[C ]est
E 58mV Log10
[C ]int
Un altro esempio
una cellula
Supponendo che la membrana di una
cellula sia permeabile solo al Na+,
calcolare il potenziale di membrana
[C ]est
E 58mV Log10
[C ]int
Corso opzionale III anno SB
Percorso Biomolecolare
Tossicologia, Fisiologia e Farmacologia
cellulare-molecolare
UD1 Fisiologia cellulare e molecolare (M. Toselli)
UD2 Farmacologia cellulare e molecolare (D. Curti)
UD3 Tossicologia (O. Pastoris)
6 CFU totali
Equilibrio di Donnan
to
t1
t2
fusso dovuto al gradiente di concentrazione
fusso dovuto al gradiente elettrico
La lunghezza delle frecce indica l’intensità dei flussi
All’equilibrio, applicando
l’equazione di Nernst sarà:
Ovvero:
[ K ]1 [Cl ]2
[ K ]2 [Cl ]1
EK ECl 58Log
[ K ]1
[Cl ]2
58Log
[ K ]2
[Cl ]1
(Equazione di Donnan)
Nota
Come diventa l’equazione di Donnan se è presente uno ione bivalente
come ad es. il Ca2+ oltre ad uno ione monovalente come ad es il Cl-?
All’equilibrio, applicando
[Ca ]1
[Cl ]2
58
Log
58Log
l’equazione di Nernst sarà: ECa ECl
2
[Ca ]2
[Cl ]1
ovvero,
e quindi,
Log
[Ca ]1
[Cl ]2
2Log
[Ca ]2
[Cl ]1
2
[Ca ]1 [Cl ] 2
[Ca ]2 [Cl ]21
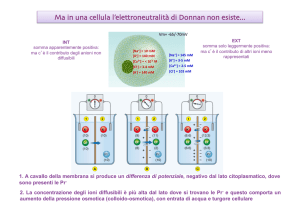
Conseguenze:
Viene prodotta una differenza di potenziale
transmembranaria ΔV stabile nel tempo;
La concentrazione totale degli ioni
diffusibili (K+ e Cl-) è maggiore dal lato
dove si trova lo ione non diffusibile (Pr-):
[K+]2+[Cl-]2>[K+]1+[Cl-]1
Vi è un aumento di pressione osmotica
dal lato dello ione non diffusibile
Problema
Supporre che a cavallo della membrana, che è permeabile a K+ e Clma non a A-, si stabilisca un equilibrio di Donnan e che la
concentrazione all’equilibrio di K+ e Cl- fuori dalla cellula sia quella
indicata in tabella.
fuori (mM)
dentro (mM)
K+
6.7
? (13.3)
Cl-
6.7
? (3.3)
A-
0
10
1) Calcolare le concentrazioni di K+ e Cl- dentro alla
cellula all’equilibrio;
2) Calcolare il potenziale di membrana Vm.
fuori (mM)
dentro (mM)
K+
6.7
? (13.3)
Cl-
6.7
? (3.3)
A-
0
10
Strumenti e conoscenze necessarie alla risoluzione del problema:
[K ]est [Cl ] int
[K ] int [Cl ]est
Equazione di Donnan:
Principio di elettroneutralità delle soluzioni: [K ] int [Cl ] int [ A ]
6.7
[Cl ] int
6.7
[Cl ] int 10
Sistema di 2
equazioni in 2
incognite
[Cl ] int x
x 2 10 x (6.7)2 0
x 3.3
Equazione di Nernst:
Vm EK 58Log
[K ]est
[Cl ] int
ECl 58Log
17mV
[K ] int
[Cl ]est
GENESI DI UN
POTENZIALE DI DIFFUSIONE
Si genera quando la membrana è permeabile in misura diversa alle varie specie ioniche
1
2
1
2
++-
Na+Cl100 mM
K+Cl-
100 mM
t1
Na+
1
K+
++-
t2
Na+
2
+
+
+
+
---
+
+
+
--
K+
pK>pNa
pK>pNa
fK>fNa
fK=fNa
Il suo raggiungimento comporta:
Equilibrio elettrico ma squilibrio elettrochimico
Flusso netto non nullo delle varie specie ioniche
Un potenziale di diffusione non si mantiene indefinitivamente
Confronto tra potenziale d’equilibrio e di diffusione
Potenziale di equilibrio:
Le specie ioniche diffusibili sono all’equilibrio elettrochimico
(vale l’equazione di Nernst)
Il potenziale di membrana coincide con il potenziale di
equilibrio di ciascuna specie ionica diffusibile (Vm=Ei)
Il potenziale di equilibrio si mantiene indefinitamente
Potenziale di diffusione:
Le specie ioniche diffusibili non sono all’equilibrio
elettrochimico (non vale l’equazione di Nernst)
Il potenziale di membrana non coincide con il potenziale di
equilibrio di alcuna delle specie ioniche diffusibili (Vm≠Ei)
Il potenziale di diffusione non si mantiene indefinitamente
Cl
Pr
-
-
+
Na
Riassumendo
Il potenziale di membrana è una conseguenza di una
permanente differenza di concentrazione ionica ai due
capi della membrana
Questa è prodotta da:
• una membrana selettivamente permeabile (potenziale
di diffusione)
• la presenza di specie ioniche non permeanti (equilibrio
di Donnan)
• un trasporto attivo degli ioni Na+ e K+
Quesito del giorno
Consideriamo un ipotetico sistema a due compartimenti separati da una membrana
permeabile al K+ e al Cl-, ma non all’anione A-. La concentrazione iniziale delle varie
specie ioniche e’ la seguente (in mM):
Int
Ext
A- =100
A- = 0
K+ =150
K+ =150
Cl- =50
Cl- =150
1) Quali concentrazioni finali raggiungera’ ciascuna specie
ionica all’equilibrio elettrochimico?
2) Che differenza di potenziale si generera’ ai due capi diella
membrana all’equilibrio elettrochimico?
3) All’equilibrio elettrochimico vi e’ anche equilibrio osmotico?
Se no, in quale direzione si muoveranno le molecole d’acqua?
1) Ricordare la regola di Donnan: [K]Ext / [K]Int =[Cl]Int/[Cl]Ext
2) Per soddisfare il principio di elettroneutralita delle soluzioni, quantita’ uguali di
K+ e Cl- devono spostarsi da Ext a Int
3) L’equazione di Nernst dice che: V = EK = ECl =….
All’inizio:
[Int]
[Ext]
100- (A)+ 50-(Cl) = 150+(K)
150-(Cl)=150+(K)
vale il principio di elettroneutralità delle soluzioni
Il Cl- tende a diffondere da Ext a Int spinto dal grad. di conc., così
pure il K+, lui spinto dal grad. elettrico che si viene a formare.
Ma dato che il principio di elettroneutralità delle soluzioni vale non
solo all’inizio ma anche all’equilibrio elettrochimico,
allora, quantità uguali di Cl- e K+ devono muoversi da Ext a Int.
Quindi sarà:
[K]Ext [Cl]Int
[K]Int [Cl]IExt
150 x 50 x
150 x 150 x
Quindi,
Vm 58Log
x = 30
150 30
50 30
58Log
10.2mV
150 30
150 30