a(t)

MOTI
Meccanica:
branca della fisica che studia il moto dei
corpi e le forze che lo fanno variare
Cinematica:
descrive il moto dei corpi senza fare
riferimento esplicito alle forze che
agiscono su di essi
Dinamica:
è lo studio della relazione esplicita tra le
forze ed il loro effetto sul moto
Per descrivere un moto è necessario specificare la posizione del
corpo in ogni istante. E’ quindi necessario definire un sistema di
coordinate:
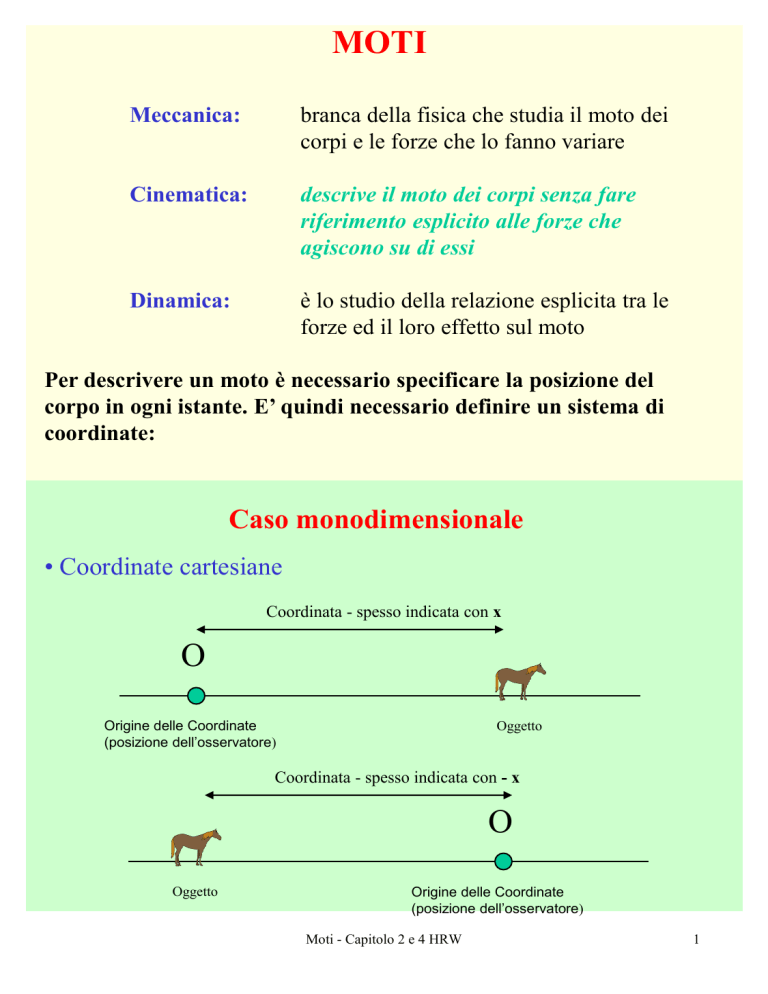
Caso monodimensionale
• Coordinate cartesiane
Coordinata - spesso indicata con x
O
Origine delle Coordinate
(posizione dell’osservatore)
Oggetto
Coordinata - spesso indicata con - x
O
Oggetto
Origine delle Coordinate
(posizione dell’osservatore)
Moti - Capitolo 2 e 4 HRW
1
Caso Bidimensionale
• Coordinate Cartesiane
• Coordinate Polari
• Ascissa x
• Ordinata y
• Distanza Radiale r
• Angolo 
r
y
O

x
O
---> (r, )
---> (x,y)
E’ ovviamente possibile trasformare le coordinate cartesiane in
polari e viceversa
x  r cos 
r  x2  y2
y  r sin(  )
  arctan  
 y
x
Moti - Capitolo 2 e 4 HRW
2
Per descrivere un moto è necessario, una volta specificata la posizione
del corpo, definire lo spostamento, la velocità e l’accelerazione.
Spostamento: lo spostamento di un corpo è il vettore il cui modulo è la distanza fra
la posizione iniziale e la posizione finale del moto misurata lungo la retta che li
congiunge. La direzione è quella della retta che congiunge la posizione iniziale con la
posizione finale. Il verso è quello rivolto dalla posizione iniziale alla posizione finale.
Tanto più la posizione iniziale e la finale distano nel
tempo tanto meno ‘preciso’ risulta essere il vettore
spostamento.
Per definire lo spostamento è necessario aver definito in
precedenza sia l’origine del sistema di coordinate che il
sistema di coordinate da usare. Altrimenti non sapremmo
da dove far partire il vettore posizione.
s  op  op
01
1
0
A mano a mano che si considerano due posizioni sempre più vicine nel tempo il
vettore spostamento diventa sempre più simile ad un segmento della traiettoria.
Portando questo ragionamento al limite è possibile definire il vettore spostamento
infinitesimo ds che descrive lo spostamento tra due posizioni infinitamente vicine
ds
ds dsdsds
ds
Il vettore spostamento infinitesimo
risulta quindi essere un segmentino
della traiettoria.
La traiettoria risulta essere composta
dalla somma di tutti i vettori
spostamento infinitesimo.
Moti - Capitolo 2 e 4 HRW
3
ATTENZIONE
La traiettoria
spazio xyz).
è il percorso del corpo nel piano xy (o nello
Attenzione: lo spostamento s nell’intervallo t0,t può non
coincidere con la traiettoria !
Moti - Capitolo 2 e 4 HRW
4
Equazione Oraria
OP  f (t )
t  tempo
OPx  3t  5
37
OPy    log 3t 
t
s1
sx
sy
s2
t3
s1
t2
t1
t
t2
s2
t1
t
s3
L’equazione oraria permette di determinare le componenti del
vettore posizione del corpo in studio in qualsiasi istante di tempo t
Moti - Capitolo 2 e 4 HRW
5
Il concetto di diagramma orario
è cosa ben diversa dalla traiettoria
Nel diagramma orario l’asse delle x rappresenta il tempo,
quello delle y una coordinata
Un moto mono-dimensionale si rappresenta in un diagramma orario a 2D
Moti - Capitolo 2 e 4 HRW
6
Per descrivere un moto è necessario, una volta specificato lo spostamento,
definire quanto velocemente un corpo si muove
Velocità:
La velocità di un corpo è, per definizione, il rapporto fra lo spazio
percorso (cioè lo spostamento) e l’intervallo di tempo impiegato per
percorrerlo
Poiché ho bisogno del vettore spostamento, anche la velocità
dovrà essere un vettore.
Modulo:
|vettore spostamento| / intervallo di tempo
Direzione: quella del vettore spostamento
Verso:
quella del vettore spostamento
Tanto più la posizione iniziale e la finale distano nel tempo
tanto meno ‘preciso’ risulta essere il vettore velocità
A mano a mano che si considerano due posizioni sempre più vicine nel tempo il vettore
spostamento, e la velocità, diventano sempre più prossimi alla tangente alla traiettoria.
Portando questo ragionamento al limite è possibile definire il vettore velocità istantanea
v(t) che dà la velocità di un punto materiale nell’istante t. La velocità istantanea risulta
essere tangente alla traiettoria
s
s
ds
v  12  vist  lim 12 
t 2 t1 t  t
t 2  t1
dt
2
1
Moti - Capitolo 2 e 4 HRW

m
v 
s
7
Diagramma Orario
ds
vist 
dt
Curva di velocità
Problema svolto 2.2 – pag. 16 – HRW
Moto di una cabina di ascensore
Moti - Capitolo 2 e 4 HRW
8
v
Xc  Xb
Xc  Xb
ds
 vist  lim

tc tb t  t
t c  tb
dt
c
b
In un diagramma orario la velocità istantanea calcolata nel punto generico x
rappresenta il coefficiente angolare della retta tangente la traiettoria nel
punto x
x
Moti - Capitolo 2 e 4 HRW
ds ( x)
v( x) 
dt
9
Per descrivere un moto è anche necessario, una volta specificato lo
spostamento e la velocità, definire quanto velocemente un corpo cambia la
sua velocità
Accelerazione:
L’accelerazione di un corpo è, per definizione, il rapporto fra il vettore
variazione di velocità istantanea e l’intervallo di tempo associato
Poiché ho bisogno del vettore variazione di velocità, anche la
accelerazione dovrà essere un vettore.
Modulo:
|vettore variazione di velocità| / intervallo di tempo
Direzione: … dipende da caso a caso
Verso:
… dipende da caso a caso
Tanto più la velocità iniziale e la finale distano nel tempo tanto
meno ‘preciso’ risulta essere il vettore accelerazione
A mano a mano che si considerano due posizioni sempre più vicine nel tempo è
possibile definire il vettore accelerazione istantanea a(t) che dà la accelerazione di un
punto materiale nell’istante t.
v v
v v
dv
a  2 1  aist  lim 2 1 
t 2 t1 t  t
t2  t1
dt
2
1
a  m2
s
Nota:
Lo spostamento infinitesimo è un segmentino di traiettoria
La velocità istantanea è sempre tangente alla traiettoria
L’accelerazione può avere un orientamento qualsiasi rispetto alla traiettoria
Moti - Capitolo 2 e 4 HRW
10
Analogamente che per lo spostamento….
v  g (t ) 
d f (t )
dt
t  tempo
vx  3
vy 
37 1

2
t
t
Permette di conoscere le componenti della velocità
di un corpo in qualsiasi tempo t
vx
vy
t
t
Un discorso analogo vale per l’accelerazione
Accelerazione, velocità e spostamento sono legate tra loro
da relazioni matematiche
Moti - Capitolo 2 e 4 HRW
11
x  at 2
v  2at
a  2a
Moti - Capitolo 2 e 4 HRW
12
Moti - Capitolo 2 e 4 HRW
13
 x2  x1  dx
• Spostamento infinitesimo ds  s12  
 y2  y1  dy
 z  z  dz
 2 1
• Velocità istantanea
v x
ds 
v(t ) 
 v y
dt 
v z
• Accelerazione istantanea
 ds x  dx
 dt 
dt
 ds

 y  dy


dt

 dt
 ds z  dz

 dt
 dt 
 d 2 sx
 dv x
 2
 dt
 dt2

2
dv  dv y d s  d s y
a

 2  2
dt  dt
dt
 dt2
dv
 z
 d sz

 dt 2
 dt

 v x (t ) dt
 a x (t )dt






s (t )   v(t )dt   v y (t ) dt   a (t ) dt   a y (t )dt


v
(
t
)
dt
a (t )dt


z

  z
 a x (t )dt



v(t )   a (t ) dt   a y (t )dt

a (t )dt

 z
Moti - Capitolo 2 e 4 HRW
14
Composizione dei moti (moto del proiettile)
Un proiettile di massa m viene sparato con velocità v = 25 m/s ad
un angolo  rispetto al suolo. Qual è la traiettoria? Qual è la gittata
del cannone? Quale è la massima altezza raggiunta dal proiettile?
(Trascurare l’attrito).
Quale sarebbe l’angolo che massimizza la gittata ?
Moti - Capitolo 2 e 4 HRW
15
Moto Circolare
Coordinate Polari (1D)
r

v
x  r
θ  spostamento angolare
(rad )
x  spostamento tangenziale
  velocità angolare
vt  velocità tangenziale
dθ

dt
vt 
dx
dt
vt  r 
(rad / s )
aθ  accelleraz ione angolare
d d 2 θ
aθ 
 2 (rad/s 2 )
dt
dt
2
 (t )
 (t )
 (t ) 
2
T (t ) 
( m)
(m/s)
at  accelerazi one tangenziale
dvt d 2 x
at 
 2 (m/s 2 )
dt
dt
at  r a
(s)
( s 1 )
T (t ) 
2r
vt (t )
(s)
 (t ) 
vt (t )
2r
( s 1 )
Nota:
Quando  è costante prende il nome di pulsazione
Moti - Capitolo 2 e 4 HRW
16
Obiettivi generali degli esercizi svolti in aula:
 Saper ricavare velocità ed accelerazione, nota la
legge oraria;
 Saper ricavare il vettore posizione, noto il vettore
velocità o il vettore accelerazione. Quando possibile,
sapere anche calcolare l’equazione della traiettoria
(per esempio: moto del proiettile).
Moti - Capitolo 2 e 4 HRW
17