Nessun titolo diapositiva - e

Termodinamica chimica :
determinare qual è la forza propulsiva delle trasformazioni chimiche
e prevederne la spontaneità.
Tiene conto SOLO delle proprietà macroscopiche della materia (P, T, V)
senza preoccuparsi della sua struttura atomica e molecolare.
Le leggi della Termodinamica sono pertanto sganciate dalle teorie
atomiche.
OBIETTIVI
-Prevedere quali processi chimici e fisici sono possibili
ed in quali condizioni;
-Calcolare quantitativamente le proprietà dello stato di equilibrio
risultante quando si sviluppa un processo
LIMITAZIONI
- Non consente di prevedere la velocità di un processo (cinetica);
- Non spiega perchè le sostanze devono avere certi valori delle proprietà
macroscopiche.
Modelli astratti
per rappresentare sistemi e processi del mondo reale
- condizioni controllate di laboratorio
- impianti di produzione industriale
- sistemi viventi
Sistema: porzione di Universo che costituisce l'oggetto della indagine
Ambiente: tutto il resto dell'Universo
Esempio
Sistema
Ambiente
Sistema
Ambiente
Sistema isolato: non può scambiare né materia né energia con l'ambiente
Vaso di Dewar isolante
Esempio
Sistema
Vuoto
Sistema chiuso: i confini impediscono lo scambio di materia (non di energia)
con l'ambiente
Esempi
+
Pistone
Mobile
Luce e
Calore
–
Pila
Sistema aperto: i confini permettono lo scambio con l'ambiente sia di materia
che di energia
Vapore
Calore
Sistema
Sistema omogeneo :costituito da UNA SOLA FASE (porzione di materia
uniforme in ogni punto sia per composizione chimica che per stato fisico)
Sistema eterogeneo : costituito da PIU' FASI
La porzione rimanente dell’Universo che può scambiare energia (e
materia) con il sistema chiuso (aperto) durante il processo in esame è
l’AMBIENTE
Fornisce le forze esterne che provocano le variazioni delle
proprietà del sistema durante un processo.
SISTEMA + AMBIENTE = UNIVERSO
Stato termodinamico del sistema :
specifica condizione macroscopica nella quale tutte
le sue proprietà macroscopiche (volume, massa, T , P)
sono note, definite (conoscendo alcune variabili) e
mantenute costanti nel tempo
intensive
estensive
Un processo termodinamico modifica
lo stato termodinamico del sistema
reversibile
irreversibile
Intensive: il loro valore NON DIPENDE DALLA MASSA
del sistema
TEMPERATURA, PRESSIONE, DENSITA', ...
Estensive:
il loro valore DIPENDE DALLA MASSA del sistema
MASSA, VOLUME, PESO, ENERGIA, ...
Variabili di stato: lo stato di un sistema è definito quando si
possono assegnare valori definiti a tutte le proprietà fisicamente
misurabili del sistema (variabili), ad es. P, T, V, ... Quelle variabili
il cui valore dipende solo dallo stato del sistema, ma non dal
particolare modo in cui si è giunti a tale stato, si dicono
variabili o funzioni di stato.
Dopo che il sistema è stato preparato stabilendo un insieme
di vincoli nell’ambiente (ad es. T o P costanti),
quando nessuna delle proprietà cambia nel tempo,
il sistema ha raggiunto l’equilibrio.
Termodinamica: scienza delle relazioni tra calore e lavoro
termochimica:
studia la quantità di calore assorbito o
sviluppato nelle reazioni chimiche
ad es. combustione di un carburante
Energia: proprietà della materia
potenziale (capacità) di muoversi
esiste in forme diverse che possono convertire una
nell’altra : termica, luminosa, elettrica, cinetica,…
Energia cinetica: associata ad un oggetto in virtù del suo moto
½ mv2 = Kg m2/s2 = Joule unità estremamente piccola
(P=L/t; watt = 1 J/s
1 watt h = 3600J; 1 Kwatt h= 3.6 x 106 J
caloria=unità di misura dell’Energia (non-SI) usata dai chimici
quantità di calore (energia) richiesta per innalzare la T di 1 g
di H2O di 1°C da 14.5°C a 15.5 °C
1 cal = 4.184 J
Energia potenziale: associata ad un oggetto in virtù della
sua posizione in un campo di forze
Lavoro :
si compie lavoro ogni qualvolta un
mosso/spostato contro una forza contraria
oggetto
viene
L=Fxl
erg = 1 dine x 1cm
joule = 1 N x 1 m
1 J = 107 erg
Eseguendo lavoro su un sistema varia l’Energia del sistema.
Il lavoro meccanico causa ΔEcin o ΔEpot
Lavoro meccanico di espansione :
un gas si espande in un cilindro dotato di stantuffo mobile
passando da Vi a Vf contro una pressione esterna P :
L = F × Δh = P × A × Δh = P × ΔV
L = P × ΔV =
Pascal × m3 = J
1 L atm = 101,325 J
Energia interna U:
contenuto di energia totale
di un sistema.
In un sistema chimico è la somma di vari contributi:
- energia potenziale intermolecolare
-energia cinetica molecolare
-energia chimica immagazzinata dai legami chimici
U : è associata alle forze attrattive e repulsive fra
tutti i nuclei e gli elettroni nel sistema
-può essere cambiata solo variando lo stato del sistema, ad es.
scambiando Lavoro meccanico.
-non è possibile determinarne il valore assoluto, ma solo le
variazioni (ΔU).
Calore o energia termica :
energia che passa in un sistema o fluisce dal sistema in
seguito ad una differenza di T tra il sistema termodinamico e
l’ambiente.
Come il lavoro, anche il calore rappresenta una modalità con la
quale è scambiata energia tra un sistema ed il suo ambiente.
Il calore fluisce da una regione a T1 maggiore (molecole più veloci) ad
una a T2 minore (molecole più lente).
Finchè un sistema ed il suo ambiente sono in contatto termico (cioè non
termicamente isolati)
si ha scambio di energia (calore) tra essi
per mantenere la loro T uguale (equilibrio termico).
Quando T1 = T2 (molecole a stessa vm), il flusso di calore si arresta.
Calorimetro :
per misurare la quantità
di energia trasferita come
calore.
Se una quantità di calore è trasferita
dal sistema al bagno, una parte del
ghiaccio fonde ed il volume della
miscela acqua e ghiaccio diminuisce.
Dalla variazione di volume del
contenuto del calorimetro si
determina la quantità di calore
trasferito.
L’equivalenza di calore e lavoro come mezzi per il trasferimento
dell’Energia fu suggerita da Benjamin Thompson (1798), consigliere
militare del re di Baviera.
Notò che : - la quantità di calore prodotto nel perforare i cannoni
era proporzionale alla quantità di lavoro eseguito:
- il calore non è un “fluido” contenuto nel metallo,
perchè l’operazione poteva andare avanti all’infinito.
J. Mayer e J. Joule dimostrarono (dal 1840) che la T di una
sostanza può essere innalzata sia compiendo su di essa lavoro
sia fornendo calore.
Una pala mossa dalla caduta di un
peso agita l’acqua in un serbatoio.
Così viene eseguito lavoro sull’acqua
e la sua T aumenta.
L’esperimento è effettuato in un contenitore
coibentato in modo da impedire trasferimento
di calore tra sistema ed ambiente.
La caloria quindi non va più considerata
come un’inità indipendente e viene definita
come:
1 cal = 4.184 J
Calore e Lavoro sono energia in transito:
- se ΔE è causata da contatto meccanico del sistema con l’ambiente, è
compiuto LAVORO;
-se è causata da un contatto termico, è trasferito CALORE (finchè non si
realizza l’uguaglianza delle T).
Spesso sia il LAVORO che il CALORE attraversano i confini del sistema
e la variazione di energia interna (ΔU) è la somma dei due contributi.
Primo principio della termodinamica:
ΔU = Q + L
Q e L dipendono dal processo (percorso) che unisce due stati,
ma la loro somma ΔU è indipendente dal percorso, quindi
U è una funzione di stato.
In qualunque processo, il calore ceduto al sistema è rimosso
dall’ambiente :
Q sis = - Qamb
Allo stesso modo, il lavoro compiuto sul sistema è fatto dall’ambiente :
Lsis = - Lamb
Sommando le due relazioni si ottiene:
ΔUsis = - ΔUamb
Pertanto, le variazioni di energia del sistema e dell’ambiente
hanno lo stesso valore, ma segno opposto.
La variazione dell’energia totale dell’universo (sistema +
ambiente) è quindi:
ΔUuniv = ΔUsis + ΔUamb
In qualunque processo l’energia totale dell’universo rimane invariata;
l’energia totale si conserva mentre è scambiata tra sistema ed ambiente.
Il lavoro non è una funzione di stato :
- se il processo è effettuato in modo repentino il lavoro è <
-se il lavoro è effettuato in modo reversibile, il lavoro è
notevolmente >
una trasformazione reversibile fornisce il max lavoro
ottenibile.
si può tornare allo stato iniziale senza che né il sistema né
l’ambiente subiscano modifiche permanenti di entità
apprezzabile
si procede mediante una serie infinita di stati, in ciascuno
dei quali il sistema è in equilibrio
per realizzare una trasformazione reversibile occorre un
tempo infinito
?
?
l1
?
1 kg
1 kg
(1)
(2)
Processo irreversibile
0,998 kg
0,999 kg
(2)
(3)
1 kg
l2
l1
(1)
(2)
Processo irreversibile
1,999
kg
l2
Processo reversibile
2 kg
2 kg



0 kg
(1)
?


l1
l2
?
Processo irreversibile:
procede
in
modo
spontaneo e i valori
delle sue funzioni di
stato differiscono di
quantità finite da un
istante al successivo
della
trasformazione
(naturale).
Qrev > Qirrev
Processi
Processi reversibili
reversibili ed
ed irreversibili
irreversibili
?
Processo reversibile:
procede in modo che
i valori delle sue
funzioni di stato non
differiscano più di un
infinitesimo tra due
istanti successivi della
trasformazione (ideale).
Lrev > Lirrev
1,998
kg
1 kg
l1
l1,001
l1,002
l2
(1)
(2)
(3)
()
Processo reversibile

0 kg
()
Calore
Calore
+Q
Sistema
-Q
Lavoro
Lavoro
-L
Sistema
+L
Energia cinetica
v
E = ½ mv2
Energia potenziale:
di gravità
(a)
(b)
Energia potenziale:
elastica


(a)
(b)
chimica
TNT
(a)
(b)
1 Erg = 10-7 J ; 1 litro x atmosfera = 101,3 J
1 eV = 1,602 • 10-19 J
; 1 caloria = 4,184 J
CICLICHE:
se il sistema torna allo stato iniziale;
ISOTERME:
se avvengono a temperatura costante;
ISOBARE:
se avvengono a pressione costante;
ISOCORE:
se avvengono a volume costante;
ADIABATICHE: se avvengono senza scambio di calore.
Primo Principio della Termodinamica
I° ENUNCIATO:
L'Energia NON si crea NE' si distrugge, ma si TRASFORMA
h
Esperienza di Joule:
Equivalente elettrico
equivalente meccanico della
della caloria
caloria
1 cal = 4,184 J
2° Enunciato: L'energia interna U di un sistema è una
funzione di stato
Sistema Chiuso
Stato I
U2 = U 1 + Q - L
Scambia calore Sistema Chiuso
Stato II
e lavoro con
l'ambiente
;
DU = Q -L
U 2 - U1 = Q - L ;
Processi ciclici
Stato I
UFINALE = UINIZIALE
;
DU = O
;
Q=L
U è una variabile estensiva, di cui si possono misurare
SOLO le variazioni
I° principio della termodinamica: principio di equivalenza
la scomparsa di un certo tipo di energia deve essere
accompagnata dalla comparsa di una equivalente quantità di una
forma diversa di energia
pertanto le varie forme di energia si trasformano una nell’altra
secondo rapporti fissi che vengono valutati mediante le
trasformazioni cicliche (stato iniziale e finale coincidono)
ΔU = Q – L = 0
Q = L
Processi adiabatici
(Q = O)
DU = - L
Processi isocori
(L = O)
DU = Qv
Processi isobari, con solo lavoro
di espansione
L = + PDV
DU = Qp - PDV
;
Qp = DU + PDV
H = U + PV
ENTALPIA
Per una trasformazione isobara DH = DU + PDV
DH = Qp
H è una funzione di stato come U, e come per U se ne misurano le
variazione DH, ma non il valore assoluto, che non è determinabile.
H è variabile ESTENSIVA.
L’energia interna e l’entalpia sono grandezze simmetriche
che si utilizzano in caso di volume costante ΔU = Qv
o pressione costante ΔH = Qp
Si valuti la differenza tra D H e D U per una reazione :
poiché D H = D U + D(PV)
la differenza è racchiusa nel termine D(PV).
Nelle reazioni a cui partecipano solidi e liquidi, DV sono trascurabili,
per cui D (P V) = 0
eDH =DU
Per le reazioni tra gas, P V = n R T
da cui D(P V) = (D n) R
e quindi D H = D U + (D n) R T
Nelle reazioni tra gas vi è differenza tra DH e DU solo quando nel
passaggio da reagenti a prodotti si ha Dn diverso da 0.
E’ possibile misurare la variazione del contenuto energetico di un
sistema a seguito di una trasformazione, ossia il DH, attraverso la
quantità di Qp.
E’ anche possibile calcolare teoricamente tale grandezza e anziché
conoscere il ΔH di una reazione chimica in particolari condizioni,
conviene conoscere il ΔH°, ossia la variazione di entalpia in
condizioni standard (o normale).
La funzione di stato entalpia esprime la quantità di energia che
un sistema può scambiare con l’ambiente.
Dipende da:
- la MASSA di materia del sistema
- CONDIZIONI FISICHE
- STATO di AGGREGAZIONE
- POLIMORFISMO
condizioni standard o di riferimento :
- 1 mole
- 25 °C ; 1 atm
- gas, liquido, solido
-forma cristallina stabile nelle condizioni std (ad es. grafite)
TONALITA’ TERMICA :
calore liberato o assorbito nel corso di una reazione chimica
(spesso P =cost → Qp =ΔH l’entalpia è l’energia trasferita come calore
a P cost)
reazioni ESOTERMICHE : calore liberato (–Qp) ΔH <0
reazioni ENDOTERMICHE : calore assorbito (+Qp) ΔH >0
reazioni TERMONEUTRALI : effetti termici nulli (Qp=ΔH=0)
Agitatore
Termometro
Contenitore
isolante
Contenitore
metallico
Ossigeno gassoso
ad alta pressione
Sostanza da bruciare
Acqua
Bomba d'acciaio
TERMOCHIMICA
Reazioni
Esotermiche che Liberano calore
Endotermiche che Assorbono calore
NH3
+
(g)
HCl(g)
NH3(soluz.) +
2NH3
(g)
NH4Cl(s)
HCl (soluz.)
+
DH < 0
DH > 0
NH4Cl(soluz.)
2HCl(g)
2NH4Cl(s)
DH'
DH''
2DH'
Stato di riferimento: 25°C (298,15°K) 1 atm reattivi e
prodotti nello stato più stabile.
NH3 + HCl(g)
(g)
1 atm, 25°C
NH4Cl(s) DH°
1 atm, 25°C
Entalpia standard di formazione:
H° f
½ H2 + ½ Cl2
HCl(g)
DH° = H°f
(g)
(g)
Entalpia standard di combustione:
CH4 + O2
(g)
(g)
H° c
CO2 + 2H2O(l)
(g)
Entalpia standard di formazione di alcune sostanze
H2(g) = 0
NO(g) = + 21,6 kcal/mole
HI(g) = + 6,2 kcal/mole
O2(g) = 0
S(s) = 0
NH3(g) = - 11.0 kcal/mole
H2O(l) = - 68,3 kcal/mole H2S = - 4,8 kcal/mole
Pb(s) = 0
N2(g) = 0
PbO(s) = - 52,1 kcal/mole
I2(s) = 0
Entalpie di formazione dei
composti, ΔH°f : entalpia
associata alla sintesi di 1
mole di composto a partire
dagli elementi nei relativi
stati std.
Quelle degli elementi sono
nulle per convenzione.
ΔHstd della reazione di
combustione di 1 mole di
composto in eccesso di O2 gas
La tonalità termica
(quantità di calore
sviluppato
o
assorbito a P cost)
di una reazione
chimica
dipende
solo dallo stato
iniziale e finale dei
reagenti
e
dei
prodotti, mentre è
indipendente
dal
numero
dei
processi intermedi
e dall’ordine con
cui
sono
effettuati.
Reattivi DH'
2
DH1
Stato intermedio
DH''2
Prodotti
DH1 = DH'2 +
DH''2
DH°1
C(s) + O2(g)
Stato Iniziale
DH°2
CO(g)
+ ½ O2(g)
CO2(g)
DH°3
DH°1
CO2(g)
CO + ½ O2 DH°2
DH°3
CO2(g)
C(s) + O2(g)
C(s) + O2(g)
CO(g) + ½ O2(g)
A + B
Stato Finale
DH°1 = DH°2 + DH°3
C + D
Secondo la legge di Hess:
DH°r = (H°fC + H°fD ) - (H°fA + H°fB )
(Diretta)
Elementi Componenti
DH°II = H°fA + H°fB
DH°I = H°fC + H°fD
Reattivi A + B
deve essere : DH°I = DH°II + DH°r ;
Prodotti C + D
DH°r
DH°r = DH°I - DH°II
DH°r = (H°fC + H°fD ) - (H°fA + H°fB )
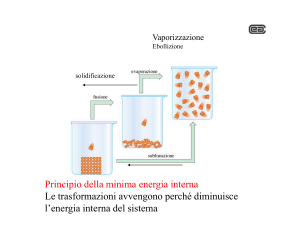
Le trasformazioni spontanee avvengono senza intervento esterno e solo
nella direzione che porta al raggiungimento dell’equilibrio.
Non conosciamo la velocità né le condizioni di reazione
necessarie per raggiungere l’equilibrio (cinetica).
- Molti processi spontanei sono esotermici (ΔH<0) :
ad es. acido + base → sale + acqua (neutralizzazione);
- ma numerosi processi spontanei sono endotermici (ΔH>0) :
ad es. - dissoluzione di NH4NO3 in acqua;
- espansione di un gas nel vuoto;
- fusione del ghiaccio
Pertanto, l’evoluzione del calore (ΔH) non è un criterio
sufficiente a determinare la spontaneità di un processo
In un processo spontaneo,
l’energia va in direzione della massima dispersione
(es. consideriamo un libro ad una certa altezza dal pavimento:
all’inizio l’energia è tutta concentrata nel libro come Epot; dopo la caduta del
grave, l’Etot è la stessa ma è dispersa nell’aria, sul pavimento, nel libro.)
La funzione di stato entropia, S, ci consente di quantizzare
questa dispersione di energia.
L’energia potenziale viene dispersa quando è convertita in energia termica.
La dispersione avviene quando l’energia è trasferita sotto forma di calore
(q).
L’effetto di una certa quantità di energia trasferita come calore (q) sulla
dispersione dipende dalla T (effetto > a basse T) e dal tipo di processo (reversibile
o irreversibile)
DS =
Qrev
T
(Rev)
DS >
Qirr
T
(Irr)
S ha la dimensioni di una energia/°K e si misura in
cal/grado (Unità Entropiche, UE) o Joule/ °K.
E' una variabile estensiva come U e H.
Secondo Principio della Termodinamica
"S è una funzione di Stato"
In un sistema isolato (es. l'Universo) sede di trasformazioni irrev
Q =O
Q
DS >
T
DS > O
"L'entropia dell'Universo tende ad un valore massimo“
Se un sistema isolato è in equilibrio, cioè sede di trasformazioni rev
Q =O
dS =
dQ
T
dQ = TdS =0 (Equilibrio)
"L'entropia dell'Universo è costante“
Se il sistema è sede di trasformazioni irreversibili (spontanee)
dS >
dQ
T
dQ < TdS
Se invece si ha, per una ipotetica trasformazione
dQ
dS <
T
(trasf. inversa spontanea)
Tale trasformazione non è spontanea, ma anzi è spontanea quella
inversa.
S è definita in modo tale che il segno algebrico della sua variazione,
considerando il valore totale di sistema + ambiente, risulti positivo
nella direzione del processo spontaneo.
La variazione di entropia ΔS si calcola come visto nel caso del ΔH:
ΔS = Sf – Si
Ad es. per la fusione del ghiaccio
H2O(s) → H2O(l)
ΔS = (63 - 41) J/K = 22 J/K
nel passaggio di stato Solido → Liquido : S aumenta
dQ = 0
dS =
dS >
dS <
(trasformazione adiabatica)
dQ
T
dQ
T
dQ
T
dS = 0
EQUILIBRIO
dS > 0
SPONTANEITA'
dS < 0
TRASF. INVERSA SPONTANEA
Processo spontaneo (irreversibile): - può avvenire da solo, senza
intervento esterno;
- segue una direzione definita.
Il I° Principio non spiega la direzionalità dei processi spontanei:
l’energia è conservata sia nel processo diretto che inverso e
nulla indica una preferenza per una direzione o l’altra.
PROCESSI FISICI SPONTANEI :
. Il calore fluisce da un corpo caldo ad uno freddo (mai il contrario).
. Un gas espande in una regione a pressione più bassa.
. Un soluto si dissolve in un solvente per formare un sistema
omogeneo.
PROCESSI CHIMICI SPONTANEI :
. una miscela di H2 e O2 brucia (se “accesa”) in modo esplosivo per
dare H2O; non si osserverà mai la decomposizione spontanea di H2O
in H2 e O2;
. 2 Na + Cl2→ 2 NaCl (spontanea)
. 2 Cu + O2 → 2 CuO (spontanea)
Entropia ed Energia sono ben diverse:
L’energia non si crea né si distrugge.
L’entropia si crea/aumenta durante qualsiasi processo spontaneo.
Quando un flusso di calore entra o esce dal sistema,
l’entropia accompagna questo flusso poichè l’energia termica
è dovuta al movimento casuale delle particelle (dispersione).
Il calore tende a rendere più disordinato il sistema verso cui
fluisce.
L. Boltzmann (1844-1906) ha correlato S con W
(n° possibili diverse disposizioni delle molecole in un sistema;
ogni disposizione ha stessa energia)
Lo stato termodinamico di un sistema può essere definito in due
modi:
1.descrizione macroscopica (P, T, V,…)
2.descrizione microscopica (proprietà delle singole particelle)
Devono coincidere poiché la prima riporta proprietà medie di tutti gli
stati microscopici del sistema.
Usando la teoria della probabilità possiamo predire e spiegare il
comportamento dell’insieme molto numeroso di atomi e molecole
che compongono un campione macroscopico di materia.
Espansione libera adiabatica di una mole di gas ideale nel vuoto :
processo spontaneo.
La probabilità che la
molecola si trovi a
sinistra sarà uguale a ½.
Direzione di un processo
spontaneo:
confronto tra la probabilità
di trovare tutte le molecole
nel lato sinistro con quella
di trovare le molecole
uniformemente distribuite
sui due lati.
In un gas formato da 4 molecole,
la probabilità che si trovino tutte
a sinistra è :
1×1×1×1= 1
2 2 2 2 16
Per N molecole, la probabilità è
1
2
6.023×1023
( )
talmente bassa da poterla
considerare nulla.
Quindi l’interpretazione statistica molecolare spiega che un gas si espande per riempire
tutto il volume disponibile perchè questa configurazione è molto più probabile di quella
in cui tutte le molecole si trovano nel lato sinistro.
Nulla impedisce la compressione spontanea di un gas,
ma l’evento è talmente improbabile da non essere mai stato osservato.
La spontaneità in Natura deriva dal comportamento casuale e statistico di
un enorme numero di molecole.
La direzionalità di un cambiamento spontaneo è una conseguenza delle
tantissime molecole presenti nei sistemi macroscopici trattati dalla
termodinamica.
Funzione di stato entropia S :
aumenta quando il processo è spontaneo.
Rimuovendo i vincoli, le molecole si muovono per
esplorare il range dei moti possibili, che ora è aumentato.
Si trova il numero di stati microscopici (microstati, W)
disponibili per le molecole :
tiene conto di tutte le possibili combinazioni delle posizioni
e delle quantità di moto disponibili per le N molecole.
Interpretazione microscopica (TERMODINAMICA STATISTICA):
l’entropia è una misura del numero di stati microscopici con
cui si può descrivere un determinato stato macroscopico
S = k ln W
W= numero dei microstati disponibili alle molecole;
k = R / N , costante di Boltzmann (1.38 × 10-23 J/K)
Quando un sistema aumenta il suo disordine significa che è aumentato
il n° di possibili disposizioni molecolari per quel sistema.
Un aumento del caos molecolare comporta un aumento di entropia.
1
I seguenti processi sono accompagnati da aumento di S :
. frammentazione di una molecola grande;
. aumento del numero di moli di gas;
. fusione di un solido;
. evaporazione di un liquido;
. mescolamento di due sostanze;
. discoglimento di una sostanza nell’altra.
I seguenti processi sono accompagnati da diminuzione di S :
. associazione di piccole molecole in molecole più grandi;
. condensazione di un gas;
. reazione di un gas per formare un solido o un liquido;
. congelamento di un liquido;
. cristallizzazione di una sostanza disciolta in un solvente;
. reazioni in soluzione per formare un precipitato.
Il fatto che in alcuni processi S diminuisce non è in contrasto
con il II° Principio della Termodinamica :
a differenza dell’Universo (dove S è costante o aumenta),
in un sistema S può diminuire.
Ciò implica che nell’ambiente S debba crescere in misura uguale
(processo rev) o maggiore (processo irrev).
Allo zero assoluto (0 K) ciascuna particella di un solido
cristallino puro e perfetto occupa posizioni precise e fisse nel
reticolo cristallino.
Poichè è assente qualsiasi tipo di disordine ed i moti termici si
annullano, il numero di microstati disponibili ad una sostanza a
0 K è pari ad 1 (uno)
(W = 1, poichè esiste solo una disposizione possibile per le
molecole) e l’entropia assoluta si annulla
S = k ln 1 = 0
E’ possibile quindi conoscere il valore assoluto dell’entropia.
Terzo Principio della Termodinamica
In un solido cristallino perfetto l'entropia si annulla
a °K (zero assoluto)
(p = cost = 1 atm)
S
cal/°k
per mole
0°K
T1
273°K
(0°C)
a 25°C e 1 atm si ottiene S°
(entropia assoluta normale)
373°K T
(100°C)
T (°K)
SOLIDO:
dQ2
dQ3
dQ1
… fino a 273°K
;dS2 =
;dS3 =
dS1 =
T2
T3
T1
QF
= 1438/273 = 5.27 UE/mole
A 273°K, fusione DSF =
TF
LIQUIDO:
dQ'
dQ''
dQ'''…
;
;
dS'=
dS'' =
dS''' =
T'
T''
T'''
… fino a 373°K
QE
A 373°K, ebollizione DSE =
TE
VAPORE:
dSI =
dQI
TI
; dSII =
273°K
S(T)
 dQ QF
+
=
TF
T
0
dQII
TII
; dSIII
373°K
dQIII …ecc
=
TIII
 dQ QE
+ 
+
TE
T
273°K
T
 dQ
+
T
373°K
Sulla base del III° principio è possibile determinare
il valore assoluto di S di un certo sistema e non solo
le sue variazioni, DS. Ciò a differenza di U e di H,
di cui si misurano solo le variazioni
Sostanza
S (cal/mol,
Sostanza
S (cal/mole
grado)
H2O (l)
Hg (l)
CCl4 (l)
He(g)
O2 (g)
16,70
18,70
51,20
30,15
48,00
grado)
C (diamante)
C (grafite)
B (s)
Fe(s)
NH4Cl(s)
0,59
1.36
1,62
6,50
22,70
L'entropia cresce con la complessità molecolare:
He < Xe < O2 < Cl2 < CH4 < C2H6 < C4H10
Inoltre, per una stessa sostanza
S cresce
Solido
Liquido
Gas
S decresce
Una molecola che si spezza in due molecole più piccole.
Aumento di moli gassose.
ΔS° = S°(prodotti) - S°(reagenti)
Calcolare la variazione di entropia std ΔS° per le seguenti reazione :
CaCO3(s) → CaO (s) + CO2(g)
S°= 92.9 J mol-1 K-1
S°= 213.74 J mol-1 K-1
S°= 39.75 J mol-1 K-1
ΔS° = (39.75 + 213.74) – 92.9 = +160.6 J mol-1 K-1
L’entropia è la prima funzione termodinamica in grado di fornire
indicazioni sulla spontaneità di una trasformazione chimica.
Il II° Principio della Termodinamica implica che :
-per un processo rev (non spontaneo), Δ S=0
-per un processo irrev (spontaneo), Δ S>0
Tuttavia
qui si fa riferimento all’Universo, mentre noi siamo interessati al
sistema dove avviene la reazione chimica.
Di norma le reazioni avvengono a T e P costanti
- a P cost il calore scambiato è ΔH = Qp
- a T cost il calore scambiato non può venire totalmente trasformato in
altre forme di energia.
Il calore può essere scomposto in due parti:
. una parte libera di trasformarsi in altre forme di energia;
. un’altra parte necessaria a mantenere il sistema alla temperatura
stabilita e quindi non utilizzabile per la conversione in altre forme di
energia.
entalpia = energia libera + energia inutilizzabile
H = G + TS
L’entalpia H di un sistema è tutta energia utilizzabile (H = G)
solo a T = 0 K quando S = 0
G = H - TS
H = U + PV
e poiché
G = U + PV
- TS
Per una trasformazione
ISOTERMA (T = Cost.) : DG = DH - TDS
Equazione di Gibbs-Helmholtz
G
è una variabile estensiva
è una funzione di stato
se ne possono misurare solo le variazioni DG,
non il valore assoluto
Per i processi isotermi ed isobari serve come:
-
Criterio di spontaneità e di equilibrio
-
Misura del massimo LAVORO UTILE
Per una trasformazione in un sistema
chiuso a P, T costanti:
1. DH = Q
Sistema
2. DG = DH - TDS
Chiuso
Se il sistema è in equilibrio (cioè è sede di
trasformazioni reversibili) si deve avere:
Q
Termostato
 Q = TDS
DS =
T
Sostituendo in (2) DG = Q - TDS = 0
Condizione di equilibrio (P, T = cost): DG = O
Se la trasformazione è irreversibile, cioè spontanea:
Q
DS >
 Q < TDS
T
DG = DH - TDS = Q - TDS < 0
Condizione di spontaneità (P,T = cost) DG < 0
G
Trasformazione
spontanea Equilibrio
Varie condizioni di spontaneità
DG = DH - TDS < 0
I - DH < 0
DS > 0
II - DH < 0
DS < 0
ma DH > TDS
III - DH > 0
DS > 0
ma DH < TDS
I
I
II
U
II
Q
U
Ghiaccio
Q
1 mole ghiaccio
Ghiaccio
Acqua
1 mole acqua liquida
Spontanea a t > O°
Spontanea a t < O°
Acqua
Fusione: processo
endotermico
Occorre considerare DS insieme a DH
Fattore Energetico
Ogni sistema tende a raggiungere il
minimo contenuto di energia
Fattore Entropico
Ogni sistema tende a raggiungere il
massimo contenuto di entropia
Ciò spiega perché nei sistemi isolati (in cui il contenuto di energia deve restare
costante) l'unico criterio di spontaneità di un processo si basa sull'aumento di S.
I Caso
DS > O
DH < O
Esempio:
SH
H2
+
Cl2
HCl
In un sistema isolato (DH=O)
una trasformazione è spontanea
se DS > 0, cioè se cresce l'entropia
II Caso
DS > O
DH = O
Se un processo avviene con
diminuzione di energia e con
aumento di entropia, esso
è spontaneo
Concordanza dei fattori energetico
ed entropico
Calore
S
Solo fattore entropico
Esempio:
Dissoluzione dello
zucchero in acqua
III Caso
Contrasto tra il fattore energetico e quello entropico
DS > O, DH > 0 (a)
DS < O, DH < 0 (b)
Esempio:
(a) FUSIONE del GHIACCIO
(b) SOLIDIFICAZIONE DELL'ACQUA
TEMPERATURA
DECIDE LA
TEMPERATURA
K
DS
DH
O(s)
HH22O
(s)
Fusione
Fusione
O(l)
HH22O
(l)
Fusione di 1 mole di H2O(s) (1 atm): DH = +1438 cal/mole
(Processo endotermico) DH > 0
Fusione di 1 mole di H2O(s) (1 atm): DS = 5,27 cal/°K
(Processo con aumento di entropia) DS > 0
All'equilibrio deve essere:
DG = DH - TeqDS = 0
DH = TeqDS
DG
DH + 1438 cal/mole
=
= 273°K
DS + 5,27 cal/°K,
mole Sopra Teq la fusione è
Teq=
+
O
-
Spontanea
solidificazione

273°
Spontanea
fusione
Teq
DS
DH
spontanea.
Sotto Teq è spontaneo il
processo opposto
(solidificazione)
T A Teq (0°C) il sistema
è in equilibrio
Scala della
TEMPERATURA ASSOLUTA
Lu = Lavoro - Lavoro di espansione = L - PDV
DG = DH - TDS = DU + PDV - TDS (1)
Q
(a) Trasformazione REVERSIBILE DS =
; Q = TDS
T
Sostituendo in (1):
DG = DU + PDV - Q;
DU = Q - L
DG = Q - L + PDV - Q = -(L - PDV) = - Lu
Lu = - DG
Q
(b) Trasformazioni Irreversibile DS >
; Q < TDS
T
Lu < - DG
Energie libere standard di Formazione
Riferite a 25°C ed 1 atm
a) Elementi nella loro forma stabile a 25°C, 1 atm
G°f
= 0
b) Composti: il valore G°f corrisponde a DG° della reazione
Elementi
1 mole di Composto
(Stato Standard)
(Stato Standard)
H2 (gas, 25°C, 1 atm) + ½ O2 (gas, 25°C, 1 atm)
H2O (liq., 25°C, 1 atm)
DG° = G°f (H2O)
(1)
G = U + PV - TS
dG = dU + PdV + VdP - TdS - SdT
dQ
Per una trasformazione reversibile: dS =
; Q = TdS
T
Per il primo principio: dU = dQ - dL
Se vi è solo lavoro di espansione: dL = PdV
dU = dQ - PdV
Sostituendo in (1):
dG = (dQ - PdV)+ PdV + VdP - dQ - SdT
Semplificando:
dG = VdP - SdT
Se T = cost., dT = 0 per cui
(dG)T=cost = VdP
G
dG
= V; ovvero:
=V
P
dP T=cost
Dalla stessa relazione:
dG = VdP - SdT
se si mantiene P costante, dP = 0 per cui
dG = - SdT
dG = - S,
G
ovvero:
=-S
dT
T
P=cost
E considerando DG:
dDG
dT
= - DS
P = cost
G° è caratteristica
della sostanza
Ad una data temperatura assoluta, T,
G = G° + RT ln a
Energia libera allo stato di
riferimento della Temperatura T
Attività
(concentrazione ideale)
(Nello stato di riferimento, a = 1)
GAS
Stato di riferimento a T : P = 1 atm (gas ideale)
gas reali:
a=f • P
Attività
Coefficiente di attività
Una mole di gas ha, a T, energia libera
G = G° + RT ln f • P
SOLIDI
Per i solidi puri, a = 1,00, per cui G = G°
LIQUIDI
Per i liquidi puri, a = 1,00, per cui G = G°
SOLUZIONI
Per le soluzioni IDEALI
a=c
Per le soluzioni NON IDEALI
a=f•c
Coefficiente di attività
concentrazione
EQUILIBRI TRA LE FASI
SISTEMI AD UN COMPONENTE
singola sostanza pura che può esistere in diversi stati di aggregazione
Fusione
Solidificazione
Evaporazione
LIQUIDO
Condensazione
Sublimazione
SOLIDO
GAS
Brinazione
Pesi per regolare la
pressione
Pistone mobile
Termometro
Cilindro di vetro
1 Mole di acqua
Q
Q
Sorgente calda o fredda
t
°C
100° 0° -
P = 1 atm
Solido
Solido
Liquido
+
+
Liquido
Liquido
QF
Vapore
Vapore
QE
Q (Calore)
calore latente di fusione, QF = - calore latente di solidificazione, QSOLID
calore latente di evaporazione, QE = - calore latente di condensazione, QC
a P = cost, QF = ΔHF
QSOLIF = ΔHS
Gli equilibri tra le fasi dipendono dalla P :
la curva di riscaldamento di H2O a P= 1 torr è diversa da quella a P= 1 atm
P = 0,01 torr
T
(°C)
O°C
Solido
Solido + Vapore
Vapore
QS
P = 100 atm (76.000 torr)
(Calorie)
Q
T
(°C)
Vapore
312°C
O°C
Solido
Solido
+
Liquido
QF
Liquido
Liquido
+
Vapore
QE
Q
(Calorie)
DIAGRAMMA DI STATO
pressione
temperature di equilibrio tra le fasi
curva AO:
B
C
equilibrio solido-vapore
(come varia la P del vapore in equilibrio
pressione
L
con il solido al variare della T)
curva OB:
S
equilibrio solido-liquido
(come varia la T fusione del solido con
la P)
V
O
curva OC:
A
equilibrio liquido-vapore
(come varia la T ebollizione del liquido
con la P)
T
temperature di equilibrio tra le fasi
P
La curva che descrive l’equilibrio LIQUIDO
VAPORE
si interrompe al punto critico (Tc, Pc).
In queste condizioni la sostanza è detta
FLUIDO SUPERCRITICO
- è un gas con una P tanto elevata da avere la densità di un
liquido;
- è un liquido con una viscosità simile a quella di un gas.
E’ possibile determinare l’andamento delle curve di
equilibrio tra le due fasi in base alle relazioni della
termodinamica?
Considerando una mole di liquido in equilibrio con una mole di gas a P, T costanti,
deve essere :
G =G
L
V
Alterando di un infinitesimo dT la temperatura T e di un infinitesimo dP la pressione
P in modo tale che il sistema resti in equilibrio, si avrà:
GL + dGL = GV + dGV
dGL = dGV
dGV = VvdP - SVdT
dGL = VLdP - SLdT
VVdP - SVdT = VLdP - SLdT
(VV - VL)dP = (SV - SL)dT = DSdT
QE
DS =
QE = Calore latente di evaporazione
T
QE
dP
dT
(VV - VL)dP = QE
=
T
dT
(VV - VL)T
dP
QE > 0, perciò
> 0 (La tensione di vapore cresce con T)
dT
Trascurando VL rispetto a VV, ed assumendo valida la legge dei gas ideali per il
vapore: VV = RT/P
QE P
QE
QE
dP
=
=
= RT .
RT2
T
dT
VVT
P
1
dT
dP
Q
QE
forma differenziale
d
(lnP)
=
d
= E
;
2
P
T
T
R
R
QE
- QE
forma integrata P = cost. e RT
lnP =
+ cost
RT
lnP
P
Acqua
Alcool Etilico
Acqua
Alcool
Etilico
1
T
T
Equilibrio gas - solido
QS
dP = QS dT
ln P = + cost
2
RT
R
T
dT
QS = Calore latente di sublimazione
Equilibrio liquido- solido
dP
QF
=
dT
(VL - VS) T
QF, calore latente di fusione, > 0
Caso 1°
VL > VS
dP
dT
, allora
dT > 0
dP
> 0,
La temperatura di fusione CRESCE con la pressione
dP
dP
VL < VS
, allora
< 0,
<0
dT
dT
La temperatura di fusione DECRESCE con la pressione
Caso 2°
P
Caso 1°
Quasi tutte le sostanze
Caso 2°
Poche sostanze (H2O)
P
L
L
S
V
S
T
V
T
Principio di Le Chatelier o dell’equilibrio mobile
Quando si applica una modifica/spinta esterna ad un sistema in equilibrio,
esso reagirà in modo da opporsi alla variazione apportata, per
minimizzarne gli effetti (Henri Le Châtelier, 1884).
Il principio di Le Chatelier consente di prevedere in modo estremamente
semplice la direzione in cui evolve un sistema inizialmente all'equilibrio
in seguito ad una data perturbazione.
Equilibrio fisico liquido-vapore
diminuendo il volume del recipiente a T costante
si osserverà uno spostamento del sistema verso lo stato liquido
(condensazione del vapore) che è lo stato che occupa il minor
volume.
In tal modo il sistema all’equilibrio reagisce in modo da annullare,
per quanto possibile, la perturbazione esterna (aumento della P).
Un altro modo per perturbare un sistema all’equilibrio consiste
nel variare la sua T.
Ricordiamo che :
- reazioni endotermiche avvengono con acquisto di calore
dall’ambiente (ΔH>0);
- reazioni esotermiche avvengono
con perdita di calore, cioè cedono calore all’ambiente (ΔH<0).
L’aumento di T di una miscela all’equilibrio mediante riscaldamento
fa sì che la reazione si sviluppi in modo tale da consumare parte del
calore addizionato.
PERTANTO:
- in una reazione endotermica l’equilibrio si sposta da sinistra
verso destra (favoriti i prodotti: Keq aumenta con aumento di T) ;
- in una reazione esotermica da destra a sinistra
(favoriti i reagenti: Keq diminuisce con aumento di T).
La maggior parte delle reazioni di dissoluzione di composti ionici
è endotermica (ΔH>0) :
per il principio di Le Chatelier,
le solubilità in tali casi crescono con l’aumento della T.
Nelle dissoluzioni esotermiche (ad es. caso di CaSO4) si osserva un
comportamento opposto: le solubilità decrescono con l’aumento
della T.
pres def VI -5.ppt
760
H2O (l)
H2O (s)
soluzione
Dtcr = abbassamento del punto di
fusione
Sostanza Kcr
Acqua = 1,86°C/mole
Benzene = 5,12° C/mole
Canfora = 40° C/mole
Dteb = innalzamento del punto di
ebollizzione
Dtcr = Kcr m Dtcr temperatura Dteb Dteb = Keb m
p = pressione
osmotica
membrana
H2O
Soluz.
diluita
EVAPORAZIONE
H2O
Soluz.
diluita
OSMOSI
pres def VI - 6.ppt
SISTEMI A DUE COMPONENTI
P (T)
Riportando sulle
ordinate P
(a T = cost) si ha
un diagramma
ISOTERMO
A
Variabili: P, T, composizione
T (P)
Riportando sulle
ordinate T
(a P = cost) si ha
un diagramma
ISOBARO
B
0,75 moli B
0,25 moli A
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
XB
1,0 0,9 0,8 0,7 0,6 0,5 0,4 0,3 0,2 0,1 0
XA
P
P°A
P
T = Cost.
LEGGI DI RAOULT:
PA = P°A XA
PB = P°B XB
Ptot
Ptot = PA + PB
A
P°B
PA
PB
B
pres def VI - 7.ppt
(B) VAPORE
DISTILLAZIONE FRAZIONATA
T
(P cost)
TA
VAPORE
LIQUIDO
VAPORE
TB
LIQUIDO
A
(A) LIQUIDO
XB
B
- Quando A e B sono in soluzione alla composizione azeotropica Xc,
essi non possono essere separati uno dall’altro mediante distillazione.
- La miscela azeotropica bolle come un composto puro ad una T cost
senza intervallo di ebollizione.
TA
TA
V
V
TB
78,5°C
L
L
A
XB
C
XC
B
H2O
XC H O
2
6
C6H6O
Non sempre due liquidi sono totalmente miscibili, ma solo parzialmente
(P = cost)
a
(P = cost)
b
1
2
3
T'c
Tc
T1
T1
A
2 fasi liquide
X1
XB
X2
2 fasi liquide
T''c
B
A
lacuna di solubilità
X1
X2
B
XB
Tc = temperatura critica di solubilità
A T >Tc il sistema è omogeneo a qualunque composizione
A T1<Tc il sistema è omogeneo solo se la sua composizione è esterna alla curva
pres def VI - 8.ppt
Soluto che si ripartisce tra due liquidi tra loro
non miscibili. Si distribuisce in entrambi a seconda
della solubilità in ciascuno di essi
Liquido 1
Liquido 2
C1
C2
= K (Costante di partizione)
Componenti = 3
Fasi
= 2
V = C + 2 - F = 5 - 2 = 3
Se si fissano P, T, C1, deve essere fissa C2
Il valore di K è costante a P, t costanti
P
Gas
Soluzione
T = Cost
Applicando al gas disciolto la legge di Raoult
1
PB = P°BXB; XB =
PB
P°B
"La frazione molare del gas nella soluzione è
proporzionale alla pressione parziale del gas in
equilibrio con la soluzione"
gB
In soluzione diluita:
nB
nB
MB
~
XB =
=
= Cost. gB
nA + nB
nA
nA
XB
gB =
= Cost.' • PB
Cost.
Il peso del gas che si scioglie in un dato volume di solvente è
proporzionale alla pressione del gas.