Diapositiva 1

Il Campo elettrico
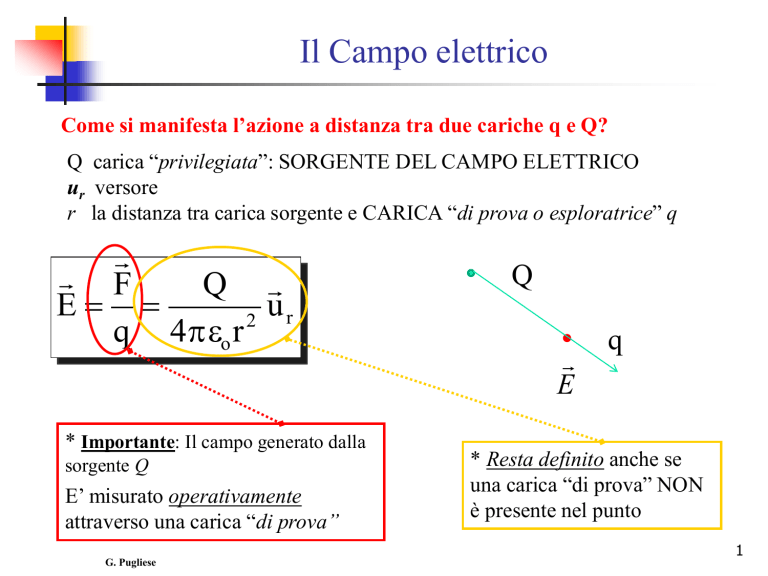
Come si manifesta l’azione a distanza tra due cariche q e Q?
Q carica “privilegiata”: SORGENTE DEL CAMPO ELETTRICO
ur versore
r la distanza tra carica sorgente e CARICA “di prova o esploratrice” q

 F
Q 
E 
ur
2
q 4o r
* Importante: Il campo generato dalla
sorgente Q
E’ misurato operativamente
attraverso una carica “di prova”
G. Pugliese
Q

E
q
* Resta definito anche se
una carica “di prova” NON
è presente nel punto
1
Linee di forza del campo elettrico
Sono una rappresentazione del campo


Sono le linee tangenti ad E(P) in ogni punto P(x,y,z) dello spazio
il numero di linee di forza per unità di area che attraversano una
superficie perpendicolare alle linee stesse è proporzionale
all’intensità del campo.
Convenzione sul
verso ….
• E(P) generato da carica q puntiforme
 Linee di forza radiali
G. Pugliese
2
Il campo elettrico di più cariche puntiformi
E’ la forza agente su una carica “di prova” q...
...per via di una data distribuzione di n cariche “privilegiate” Qi
(n = 3)


  

 F1  F2  F3
F
E

q
q
(n = 2, Q1 = Q2 = +q)
• Si è applicato il principio di sovrapposizione degli effetti
G. Pugliese
3
Esempio di calcolo del Campo Elettrico
Tre cariche positive eguali q1=q2=q3 sono fisse nei vertici di un triangolo equilatero di lato
l. Calcolare la forza elettrica agente su ognuna delle cariche e il campo elettrostatico nel
centro del triangolo.
y
Calcoliamo il campo E in P3 somma del campo prodotto da q1 e q2:
E1  E2 
1
q
40 l 2
La forza che agisce su q3:
E
E2
E  E1 y  E2 y 


F  q3 E 
1
2q cos 30
1 q 3

40
l2
40 l 2
q2 3 
uy
2
40 l
1
E1
x
P3
P1
P2
Analogamente su P1 e P2.
Nel centro C, equidistante dai vertici, i moduli dei campi generati dalle tre cariche eguali sono uguali.
G. Pugliese
4
Campo di una distribuzione continua di carica
Il campo E nel punto P si ottiene:
• Scomponendo la distribuzione di carica di densità volumetrica (oppure
superficiale o lineare) uniforme r  dq/dV in volumetti dV s opp. l  cui
corrisponde una carica dq = r dV

dE 
dq 
ur
2
40 r
• Applicando il principio di sovrapposizione


E ( P)   dE 
G. Pugliese
dV 
r ur
2

4o Q r
1
5
Esempi





Campo elettrico di un anello uniformemente carico
Campo elettrico di un disco sottile
Campo elettrico di una lastra piana indefinitamente
estesa
Campo elettrico prodotta da un doppio strato di piani
paralleli
Campo elettrico prodotto da una sbarretta carica
G. Pugliese
6
Applicazione
Tubo catodico (televisore, monitor, oscilloscopi….)
G. Pugliese, corso di Fisica Generale
7
Deflessione di una carica in un campo uniforme
• Campo elettrico uniforme come analizzatore di energia
• Moto tra le lastre cariche
 RETT. UNIFORME lungo X
x = v0t  t = x/v0
 UNIF. ACCELERATO lungo Y
y = Fel/m  vy(t) = (Fel/m)t

a  arctan[vy(B) / v0] = arctan[(q s a)/0 m v02]
Fel=qE = q s/0
(m, q)
G. Pugliese, corso di Fisica-2nda parte
Facoltà di Ingegneria, Foggia
8