Presentazione di PowerPoint

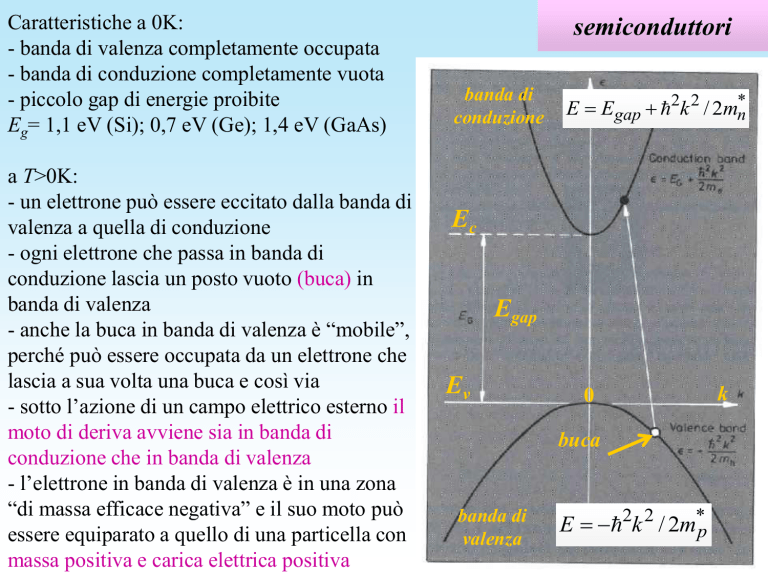
Caratteristiche a 0K:
- banda di valenza completamente occupata
- banda di conduzione completamente vuota
- piccolo gap di energie proibite
Eg= 1,1 eV (Si); 0,7 eV (Ge); 1,4 eV (GaAs)
a T>0K:
- un elettrone può essere eccitato dalla banda di
valenza a quella di conduzione
- ogni elettrone che passa in banda di
conduzione lascia un posto vuoto (buca) in
banda di valenza
- anche la buca in banda di valenza è “mobile”,
perché può essere occupata da un elettrone che
lascia a sua volta una buca e così via
- sotto l’azione di un campo elettrico esterno il
moto di deriva avviene sia in banda di
conduzione che in banda di valenza
- l’elettrone in banda di valenza è in una zona
“di massa efficace negativa” e il suo moto può
essere equiparato a quello di una particella con
massa positiva e carica elettrica positiva
semiconduttori
banda di
conduzione
E  Egap  2k 2 / 2mn*
Ec
Egap
Ev
0
buca
banda di
valenza
E  2k 2 / 2m*p
k
conducibilità elettrica nei semiconduttori
heavy
hole
light
hole
due contributi alla conducibilità:
  ne n pe p
masse efficaci piccole
diverse fra
“elettrone” e “buca”
  e / m
*
contributo degli elettroni
in banda di conduzione
contributo delle buche
in banda di valenza
conducibilità elettrica
nei semiconduttori
semiconduttore intrinseco: n=p
Calcolo di n e di p:

n

g ( E ) f F ( E , T )dE 
Ec
8
3 
2me
( E  Ec )dE
( E  E F ) / k BT
h3
e
1
Ec



3
8 2me3 E F / k BT
8

2
m
 E / k BT
e
3 / 2 E F / k BT
x

e
e
(
E

E
)
dE

(
k
T
)
e
e
x dx
c
B
3
3
h
h
E
0


c
 me k BT 
n  2

2 
 2 
3/ 2
e  ( Ec  E F ) / k B T
 mh k BT 
p  2

2 
 2 
3
legge dell’azione di massa
3/ 2
e  ( E F  Ev ) / k B T
 me mh k BT   E gap / k BT
 e
np  4


2 2


Calcolo del livello di Fermi per il
semiconduttore intrinseco
Livello di
Fermi
- ni = pi
- si assume me mh=m*
3/ 2
 m*k BT
n  2
 2 2





m k T 
n  2 e B 
 2 2 
3/ 2
e
 E gap / 2 k BT
Egap
EF
e  ( Ec  E F ) / k B T
dal rapporto: Ec-EF = Egap/2
EF = Ec - Egap/2
Stima di ni a 300K:
 m*c 2k BT 

ni  2
 2 (c)2 



16
 10 m

3/ 2
 0,2  0,5  106  3  10 2 (eV )2 
 E gap / 2k BT

e
 2
7
2


6  (2  10 eVm)


 2 3 / 2 18
e
3/ 2
e
1.1 / 2310 2
 1016 m 3
- da confrontarsi con  1029m-3 per i conduttori
- inoltre dipendenza esponenziale dalla temperatura
“drogaggio”
livello del
donatore
donatore
drogaggio tipo “n”
con un atomo
pentavalente (fosforo):
il donatore introduce
un livello energetico
Ed molto popolato
poco sotto il fondo
della banda di
conduzione Ec
accettore
livello
dell’accettore
drogaggio tipo “p”
con un atomo
trivalente (Al):
l’accettore introduce
un livello energetico
Ea molto popolato
poco sopra la cima
della banda di
valenza Ev
conducibilità elettrica
in un semiconduttore
drogato n
EF
“n”
livello del
donatore
con un drogaggio di tipo “n”
- il livello di Fermi viene a posizionarsi a metà
fra il livello Ed del donatore e il fondo della
banda di conduzione;
- gli elettroni introdotti dal donatore hanno
altissima probabilità di passare alla banda di
conduzione, per cui la densità numerica n
degli elettroni nella banda di conduzione
cresce moltissimo e diventa praticamente
eguale a nd
- per la legge dell’azione di massa, i portatori
della banda di valenza si riducono in modo
inversamente proporzionale: nd p = ni2
Tipici drogaggi
drogaggio debole:
Natomi donatori 10-8 Natomi semicond
drogaggio forte:
Natomi donatori 10-6 Natomi semicond
la conducibilità è dovuta praticamente
solo alla densità nd dei donatori
(portatori di maggioranza)
 n  nd ee
conducibilità elettrica
in un semiconduttore
drogato p
“p”
livello
dell’accettore
EF
con un drogaggio di tipo “p”
- il livello di Fermi viene a posizionarsi a metà
fra il livello Ea dell’accettore e la cima della
banda di valenza;
- le buche introdotte dall’accettore hanno
altissima probabilità di essere occupate da
elettroni della cima della banda di valenza, che
lasciano a loro volta delle buche nella banda
di valenza per cui la densità numerica p delle
buche cresce moltissimo e diventa
praticamente eguale a naccettori
- per la legge dell’azione di massa, i portatori
della banda di valenza si riducono in modo
inversamente proporzionale: n naccettori = ni2
con un drogaggio di tipo “p”, la
conducibilità è dovuta praticamente solo
alla densità na degli accettori (portatori
di maggioranza)
 p  naeh
zona “estrinseca”:
tutti i portatori di
maggioranza sono in
banda di conduzione,
la resistenza elettrica
cresce linearmente
con T perché cala la
mobilità
R (unità
arbitrarie)
resistenza elettrica in
semiconduttori debolmente drogati
zona “intrinseca”: i
portatori “intriseci”
cominciano a passare
con crescente
probabilità in banda
di conduzione, la
resistenza elettrica
diminuisce
esponenzialmente con
T perché cresce la
densità n di portatori
 (pn)
la giunzione diodo
 (np)
lato drogato n
lato drogato p
Ec
p
V=0
- i livelli di Fermi si allineano
- la densità di elettroni con E>Ecp è la
stessa nei due lati della giunzione essendo
proporzionale a exp-(Ecp-EF)/kBT
Ecn
Ev
p
Evn
- il flusso di cariche  (pn) dal lato “p”
verso il lato “n” è uguale al flusso (np)
in senso opposto
- la densità di corrente è nulla
zona di
“svuotamento”
il diodo
 (pn)
 (np)
V>0 (bias positivo)
Ec
p
Ecn
EFn
EF
Ep v
p
Evn
zona di
“svuotamento”
- si riduce la differenza (Ecp - Ecn) fra i
due livelli base della banda di conduzione;
i livelli di Fermi non sono più allineati, il
livello EFn dal lato n è più alto
- la densità di elettroni con E>Ecp è
maggiore nel lato n della giunzione che
nel lato p: infatti nel lato n è
proporzionale a exp-(Ecp-EFn)/kBT, mentre
nel lato p è rimasta allo stesso valore che
aveva in assenza di bias, proporzionale a
exp-(Ecp-EFp)/kBT
- il flusso di cariche  (np) dal lato “n”
verso il lato “p” è maggiore del flusso
 (pn) in senso opposto
- c’è una densità netta di corrente da p a n
il diodo
 (pn)
V<0 (bias negativo)
 (np)
Ec
p
EF
Ecn
Ep v
EFn
p
- cresce la differenza (Ecp - Ecn) fra i due
livelli base della banda di conduzione; i
livelli di Fermi non sono più allineati, il
livello EFn dal lato n è più basso
- la densità di elettroni con E>Ecp è
minore nel lato n della giunzione che nel
lato p: infatti nel lato n è proporzionale a
exp-(Ecp-EFn)/kBT, mentre nel lato p è
rimasta allo stesso valore che aveva in
assenza di bias, cioè proporzionale a
exp-(Ecp-EFp)/kBT
- il flusso di cariche (np) dal lato “n”
verso il lato “p” è minore del flusso
 (pn) in senso opposto
Evn
zona di
“svuotamento”
- c’è una debolissima densità di corrente
da n verso p
La caratteristica del diodo
Calcolo del flusso di elettroni:
o   ( p  n)  Ae
   (n  p)  Ae
( Ecp  EFp ) / k BT
( Ecp  EFn ) / k BT
Calcolo della densità di corrente:
J  C (  o )  Co (eeV / k BT  1)
Caratteristica del diodo:
J  J o (e eV / k BT  1)
 Ae
( Ecp  EFp eV ) / k BT
 oeeV / k BT