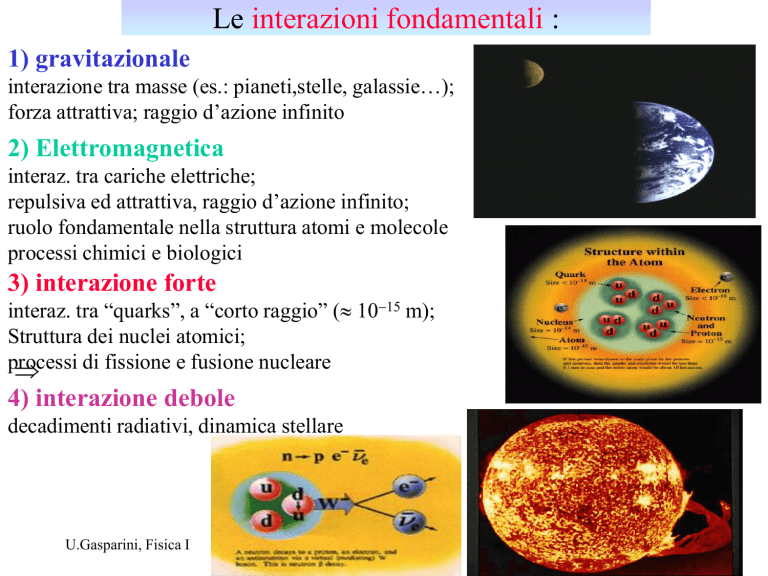
Le interazioni fondamentali :
1) gravitazionale
interazione tra masse (es.: pianeti,stelle, galassie…);
forza attrattiva; raggio d’azione infinito
2) Elettromagnetica
interaz. tra cariche elettriche;
repulsiva ed attrattiva, raggio d’azione infinito;
ruolo fondamentale nella struttura atomi e molecole
processi chimici e biologici
3) interazione forte
interaz. tra “quarks”, a “corto raggio” (-5 m);
Struttura dei nuclei atomici;
processi
di fissione e fusione nucleare
4) interazione debole
decadimenti radiativi, dinamica stellare
U.Gasparini, Fisica I
1
Principio d’inerzia
“Dinamica” : studia le relazioni tra il moto dei corpi, descritto dalle quantità
cinematiche (velocità, accelerazioni), e le “forze” (interazioni tra corpi) che lo
condizionano determinando le “variazioni dello stato di moto”
Il moto in “assenza di forze” (condizione sperimentale non realizzabile:
teoricamente, quella di un corpo infinitamente lontano da ogni altro corpo) o
in assenza di forze non equilibrate è regolato dal “principio di inerzia”
(o prima legge della dinamica, dovuta a Galileo Galilei) :
un corpo sul quale non agiscono forze, ovvero sul quale agiscono
forze che si equilibrano, persevera nel suo stato di quiete o
di moto, ossia non varia la sua velocità v
risultato di un procedimento di osservazione sperimentale
e di “astrazione”, intesa come estrapolazione dei risultati
ottenuti in una situazione reale ad una situazione ideale
di totale assenza di forze non equilibrate (ad es., attriti)
il principio d’inerzia soppianta le leggi aristoteliche del moto che associavano,
erroneamente, le forze alle velocità piuttosto che alle loro variazioni
(accelerazioni) 2
U.Gasparini, Fisica I
Intensità di una forza
“Definizione operativa” di una grandezza fisica :
definire un procedimento ripetibile di misura,
attraverso cui associare un numero alla grandezza in questione
Intensità di una “forza” applicata ad un corpo :
misurata da un “dinamometro”, strumento opportunamente tarato;
l’operazione di “taratura del dinamometro” va considerata come parte
integrante della definizione operativa della grandezza fisica “forza”.
Schematicamente:
oggetto deformabile che risponde
in maniera riproducibile ad una
sollecitazione di
trazione e/o
compressione
1 “unità di
massa” m
(arbitraria)
U.Gasparini, Fisica I
1 “unità
di forza”
( convenzionalmente :
per m 1 kg (unità di massa nel S.I.)
1 “unità di forza” 9,8 “Newton”)
unità di misura della
forza nel S.I .
…. ecc.
2 “unità di forza”
2m
3
Forze ed accelerazioni
Esperimenti sull’effetto dell’applicazione di una forza sul moto dei corpi :
1 “Newton”
a
Il corpo di massa m=1kg
subisce un’accelerazione
F
a = 1 m/s2
m= 1 kg
2 “Newton”
a
F
4 “Newton”
a
F
a = 4 m/s2
1 Newton
a
m= 2 kg
a = 2 m/s2
F
2N
a
a
U.Gasparini, Fisica I
a = 0.5 m/s2
F
4N
a = 1 m/s2
F
a = 2 m/s2
4
Forze e cambiamenti di direzione
Inoltre:
a = v2 / r = 1 m/s2
1N
v
m=1 kg
r = 1m
v= 1 m/s
a =v2 /r = 4 m/s2
m
v
4N
r
v= 2 m/s
U.Gasparini, Fisica I
5
Carattere “vettoriale” della forza e 2a legge di Newton
Forze applicate separatamente:
F=4N
m=1 kg
/2
a=4m/s2
F=3 N
a=3m/s2
Forze applicate contemporaneamente:
F
a=5m/s2
F
L’insieme delle osservazioni sperimentali sopra schematicamente riportate si
riassume nella seguente relazione vettoriale:
2a
legge della dinamica ( legge di Newton ) :
“massa inerziale”
F ma
U.Gasparini, Fisica I
6
risultante delle forze agenti sul corpo di massa m
“Quantità di moto”:
m
p m v
v
dv (t )
dmv (t )
F ma m
dt
dt
dp(t )
F
dt
Esempi:
formulazione più generale
della 2a legge della dinamica,
valida anche per situazioni
in cui m costante
i ) meccanica classica: razzo (sistema con massa variabile del combustibile)
ii) meccanica relativistica ( v @ c=3 108 m/s, velocità della luce)
“massa di riposo”
m0
m( v )
U.Gasparini, Fisica I
v2
1c2
(caratteristica intrinseca
del corpo)
7
Impulso di una forza
“Impulso” di una forza F(t) in un dato intervallo di tempo ( t1, t2 ) :
t2
J (t1 , t 2 ) F (t )dt
[J]=Ns
t1
Forze che in tempi molto brevi (infinitesimi) esercitano un impulso finito:
t 0
lim J ( ) lim
F ( t ) dt 0
0
0
t0
(ossia l’intensità della forza tende all’infinito nel tempo molto
breve considerato) si dicono “forze impulsive”.
J (ti , t
Teorema dell’impulso:
f
) p p f - pi
infatti, integrando la 2a legge di Newton:
tf
ti
U.Gasparini, Fisica I
F (t )dt
tf
ti
pf
dp(t )
dt dp p
dt
J (ti , t f )
pi
8
“Forza peso”:
E’ la forza di attrazione gravitazionale cui è soggetto un corpo a causa della Terra
Fp mg
Fp kmg
“massa gravitazionale”
Sperimentalmente, si osserva che sotto l’azione della sola forza peso,
tutti i corpi si muovono con la stessa accelerazione a = 9,8 m/s2 g :
“massa inerziale”
Fp kmg mi a mi g
legge di Newton
mg
indipendente
dalla massa
mi
g mi
k
la massa gravitazionale è proporzionale
alla massa inerziale
la costante k dipende unicamente dall’unità di misura convenzionalmente scelta
per mi , mg
mi mg
Si può porre :
Fp mg
U.Gasparini, Fisica I
(ossia k g)
9
Reazioni vincolari
La presenza di “vincoli” che limitano le possibilità di movimento di un corpo
determina lo sviluppo di forze dette “reazioni vincolari”, dipendenti dalle
altre forze agenti sul corpo (es., forza peso) e dal moto che il corpo
è vincolato a compiere
F
m
Esempi:
i ) reazione vincolare di un piano d’appoggio orizzontale
esercitata su un corpo in quiete
R mg F ma 0
F -mg
risultante delle forze
agenti sul corpo
y
ii ) reazione vincolare di un piano inclinato “liscio”
(privo d’attrito capace di sviluppare reazioni
unicamente normali alla sua superficie)
mg F ma
U.Gasparini, Fisica I
a 0
Fx 0
F y mg cos J
mg
F
J
mg
ay 0
a
a x g sin J
10
ay 0
x
Forza d’attrito statico
Descrizione fenomenologica della forza d’attrito:
i ) forza d’attrito statico:
y
F
mg
F
F
x
R ma 0
Fx 0
F y mg
attr
F
0
mg
F x - F F attr
F y mg N
attr
F
-F
Si verifica sperimentalmente:
S
F attr FMax
s N
U.Gasparini, Fisica I
“reazione
normale”
forza di
“attrito statico”
“coefficiente di attrito
statico”, caratteristico 11
delle due superfici a contatto
Equilibrio statico su un piano inclinato “scabro”
y
F
mg
F -mg
R mg F ma 0
J
x
F x - mg sin J F attr
F y mg cosJ N
S
F attr mg sin J FMax
s N s mg cosJ
tan J s
U.Gasparini, Fisica I
condizione per l’equilibrio statico
su un piano scabro con coefficiente
d’attrito statico s
12
Forza d’attrito dinamico
y
F x F attr
v
F
F y mg N
x
F attr
mg
D N
“coefficiente di attrito dinamico”,
indipendente dalla velocità
Esempio:
moto lungo un piano inclinato scabro:
y
F
mg
a
J
ma mg F
Legge di Newton:
ma mg sin J - D mg cos J
0 - mg cos J F y
Legge del moto:
x
a g (sin J - D cosJ )
v (t ) v0 at
x ( t ) x0 v0 t
1
at 2
2












