m-1

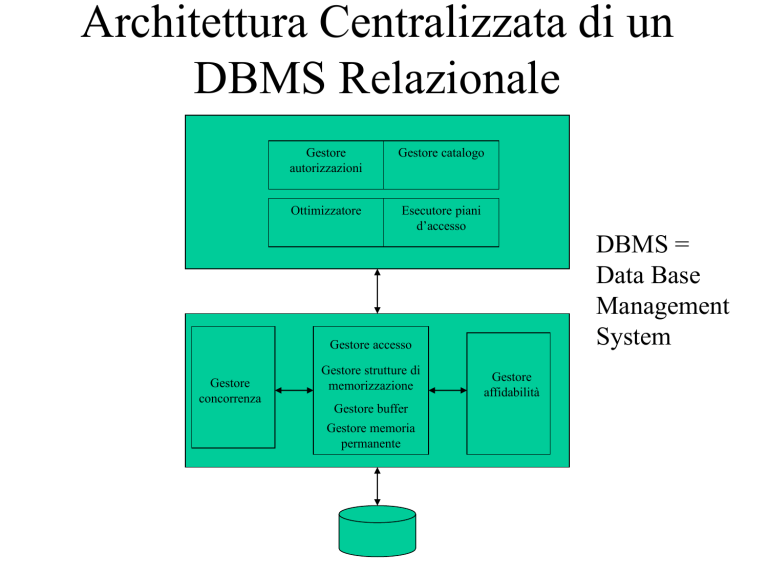
Architettura Centralizzata di un
DBMS Relazionale
Gestore
autorizzazioni
Gestore catalogo
Ottimizzatore
Esecutore piani
d’accesso
DBMS =
Data Base
Management
System
Gestore accesso
Gestore
concorrenza
Gestore strutture di
memorizzazione
Gestore buffer
Gestore memoria
permanente
Gestore
affidabilità
Gestore di buffer e interazione con il SO
gestore
buffer
buffer pool
memoria temporanea
tabella pag. residenti:
<id_pag, posiz. buffer>
- pincount
- dirty/nondirty
- pag. fisica
pagina fisica
memoria
permanente
• scrittura di una pagina da memoria temp. a permanente:
 per sostituzione, quando si deve fare spazio nel buffer ad una nuova pagina
richiesta da qualche applicativo
 per gestire in modo sicuro le modifiche fatte da una transazione o la sua fine, cioè
per via di commit o end_transaction
• modifica di pagina:
 fatta direttamente sulle pagine del buffer_pool dalle componenti del sgbd di
livello superiore rispetto al buffer mgr
 la componente che ha eseguito la modifica chiede al buffer mgr di aggiornare la
proprietá dirty/nondirty della pagina modificata
• rilascio di una pagina, per fine applicativo o transazione
 provoca il decremento del pincount
• richiesta di una pagina
 se la pagina si trova nel buffer pool il buffer_mgr incrementa il pincount di quella
pagina e restituisce alla componente che ha richiesta la pagina il riferimento a
questa nel pool
 altrimenti il buffer_mgr sostituisce una pagina residente nel buffer pool:
tra le pagine con pincount=0 sceglie$ una pagina da eliminare, naturalmente
scrivendola prima in mem. permanente se è dirty;

segnala errore se non ci sono celle con pincount a 0;
scrive nella cella di buffer pool: la pagina fisica richiesta, il pincount a 0 e la
proprietá dirty a false


aggiorna la tabella delle pagine residenti con la coppia
<cella_scelta, Id_pagina_fisica>
 incrementa il pincount di quella pagina e restituisce alla componente che ha
richiesta la pagina il riferimento a questa nel pool
$:
scelta guidata da una strategia di sostituzione (al limite LRU, sperimentalmente la
migliore in caso di accessi concorrenti)
Gruppo Basidati e Sistemi:
Gestore
della memoria
permanente
•le
pagine dovrebbero
essere una
struttura dati
valida per la riorganizzazione di insiemi di record
è la componente di un sgbd che si occupa del trasferimento
• le pagine costituiscono anche l’astrazione che la
dei dati persistenti dal buffer in memoria temporanea alla
base dati fornisce sui dispositivi di memorizzazione
memoria permanente e viceversa
fisica
“riveste” la memoria fisica permanente con una astrazione
secondo la quale:
• la memoria permanente è un insieme di bd
• una base dati è un insieme di file
• un file è un insieme di blocchi, o pagine fisiche, numerati
progressivamente e di lunghezza prefissata in cui viene
memorizzata una collezione di record (tabella o indice)
• un file logico può essere realizzato come un file fisico o parte
di un file fisico
Tempo di accesso ai dati su disco
Tempo medio trasferimento di un blocco da memoria permanente
a temporanea:
(ts + tr + tb) ms
per k blocchi contigui: (ts + tr + k * tb) ms
ts: seek time o tempo di posizionamento delle testine di lettura sul cilindro
richiesto del disco (tra 5 e 10 ms); parametro che incide di piú
tr: rotation latency o tempo di latenza è il tempo di attesa per avere un blocco
sotto la testina di lettura già posizionata sulla traccia
tb: tempo di trasferimento di un blocco
Due livelli di memoria, memoria perm. e memoria temp. sono la soluzione piú comune
per applicazioni bd; si hanno anche applicazioni ad uno o tre livelli di memoria.
un livello: tutta la base dati è gestita in memoria centrale.
Struttura interna delle pagine
intestazione o header di pagina
contiene
quantità di spazio libero
riferimento all’inizio dello spazio utilizzab.
riferimento prossima pag. libera del file
vettore di indirizzamento (possibile)
contiene
offset ai record nella pagina
Struttura interna delle pagine
riferimento ad un record o RID
• diretto
j
header
Pid, offset_in_pg
k
record
• indiretto, ad es. tramite vettore di indirizzamento
interno alla pagina
Pid, j
riferimento al record
• diretto: va bene per collezioni di dati statici
• indiretto, tramite vettore di indirizzamento: va bene per
collezioni di dati volatili o se la memoria è gestita con
spostamento dei record nelle pagine (ad esempio per
mantenere ordinamento)
Strutture per organizzare la memorizzazione di
collezioni di record in memoria permanente:
• sequenziale oppure seriale (a heap file) : i dati sono
memorizzati in pagine consecutive e ordinati secondo una
chiave/ non ordinati
• per chiave con metodo procedurale: i dati sono memorizzati
in pagine consecutive e ordinati secondo una chiave (hash)
• per chiave con strutture ad albero: i dati sono memorizzati
in strutture indice o directory + dati; è la più usata;
• per attributi non chiave: per la ricerca di un sottoinsieme di
record in base al valore di un attributo non identificatore
• per dati multidimensionali: quando i dati sono vettori che
rappresentano oggetti geometrici, immagini (GIS, CAD… )
Memorizzazione di collezioni di record in memoria
permanente
per chiave con strutture ad albero: dati memorizzati in
forma tabellare in insiemi di coppie (chiave, rid)
Per accedere velocemente ad un valore di chiave si ha:
<struttura a indice o directory , dati>
Non si possono usare alberi binari bilanciati come per la memoria
temporanea perché:
1. se non si fa attenzione al modo in cui i nodi dell’albero sono
memorizzati nelle pagine della memoria permanente la ricerca di un
elemento dell’indice puó richiedere un grande numero di accessi alla
memoria permanente;
2. per indici volatili il bilanciamento dell’albero in memoria permanente
è troppo costoso
la ricerca di un elemento dell’indice puó richiedere un grande
numero di accessi alla memoria permanente;
ESEMPIO
un indice di 1 milione di elementi richiede una media di 20 accessi
log2 1.000.000 ~ 20
se invece mettiamo nella stessa pagna opportunamente piú nodi di
un albero riduciamo gli accessi: nell’esempio sopra supponiamo di
avere 100 nodi di sottoalbero per pagina fisica
log100 1.000.000 = 3
punto 1: i nodi di un albero binario devono essere memorizzati
opportunamente nelle pagine della memoria permanente
albero binario impaginato
punto 2: il bilanciamento deve essere risolto “localmente”
dall’albero binario impaginato al B-albero
autori: Bayer e McCreight, 1972
Strutture a B-tree: albero con nodi a piú vie
sono le strutture di memorizzazione dei dati in memoria permanente
più comuni nei sgbd relazionali
• ESEMPIO: sottoalbero di un B-albero di ordine (numero massimo nodi figli) 5
..
46
..
..
..
..
50
..
55
..
60
..
65
..
..
66
..
..
79
..
..
68
..
..
71
..
..
74
..
78
..
Definizione di B-tree:
• ogni nodo interno ha la struttura seguente
[p0(k1,r1),p1,...(kj,rj),pj]
– ri è un riferimento al record di chiave ki
– pi è un puntatore ad un nodo figlio
• ogni nodo foglia ha la struttura seguente
[\(k1,r1),\,...(kj,rj),\]
• le chiavi ki in ogni nodo sono ordinate
• ogni nodo non foglia con j chiavi ha j+1 figli
• tutte le chiavi nel sottoalbero la cui radice è
puntata da pi sono comprese strettamente tra ki e
ki+1
Definizione di B-tree di ordine m (cont)
• la radice ha
0 <= nodi figli <= m
1 <=nro chiavi <= m-1
• ogni nodo interno ha
m/2nro_figli <= m
m/2-1nro_chiavi <= m-1
• tutte le foglie si trovano allo stesso livello
Ogni nodo di albero binario si fa coincidere con una
pagina del file in cui è memorizzato l’albero:
nodo = pagina
Ricerca in B-tree
• Cerca nel nodo la prima chiave ki tale che
– k=ki
– ki>k, seguire il puntatore pi-1
• Oppure, seguire l’ultimo puntatore pj del
nodo
Numero massimo di nodi in un B-albero di ordine m,
altezza h e nodi riempiti al massimo quindi con m
figli:
livello 1: 1
livello 2: m
livello 3: m * m
livello 4: m2 * m
……..
livello i: mi-1
………….
livello h: mh-1
Sh-1i0mi (mh –1)/(m-1)
Numero minimo di nodi in un B-albero di ordine m
altezza h e nodi riempiti al minimo, quindi con m
figli:
livello 1: 1
livello 2: 2
livello 3: 2 * m/2
livello 4: 2 * m/2 * m/2
……..
livello i: 2 ( m/2 )i-2
………….
livello h: 2 ( m/2 )h-2
1+2*Sh-2i0(m/2)i 1+2(((m/2)h-1 –1)/(m/2-1))
Numero di nodi:
1+2(((m/2)h-1 –1)/(m/2-1))<= Nnodi <=(mh –1)/(m-1)
Numero minimo di chiavi per un B-albero:
radice +[1+2(((m/2)h-1 –1)/(m/2-1)) –1] * (m/2 – 1) =
= 2(((m/2)h-1 –1)/(m/2-1)) * (m/2 – 1) + radice =
= 2((m/2)h-1 –1) + radice = 2(m/2)h-1 –2 +1
Numero massimo di chiavi per un B-albero:
(mh –1)/(m-1) (m-1) = mh –1
2(m/2)h-1 –1 <= Nchiavi <= mh –1
Complessità della Ricerca
in B-albero di altezza h e numero di chiavi inserite N
2(m/2)h-1 –1 <= N <= mh –1
2(m/2)h-1 <= N + 1 <= mh
 logm(N+1) <= h
 2(m/2)h-1 <= N + 1 da cui: (m/2)h-1 <= (N + 1)/2
h-1 <= logm/2 ((N+1)/2) e h <= 1 + logm/2 ((N+1)/2)
 logm(N+1) <= h <= 1 + logm/2 ((N+1)/2)
• se N è grande l’altezza h del B-albero si approssima
a logmN
• quindi il costo Cr della ricerca di una chiave
nell’albero è compreso tra 1 e h
Altezza max e min di un B-albero in funzione della
dimensione delle pagine: chiavi 10 bytes e rid 4 bytes
1000 1000
Dim
100k 100k
10k
H
h
max min
10k
H
h
max min
1M
H
h
max min
1M
H
max
pag
m
h
min
512
28
2,1
3,4
2,7
4,2
3,5
5,1
4,1
6,0
1024 56
1,7
2,9
2,3
3,6
2,9
4,3
3,9
4,9
2048 113
1,5
2,5
2,0
3,1
2,4
3,7
2,9
4,3
4096 227
1,3
2,3
1,7
2,8
2,4
3,3
2,6
3,8
Ricerca per intervallo
di tutti i record con chiave k:
v1 <= k <= v2
Cric-int = h * (v2 – v1) / (kmax – kmin )* N
(v2 – v1) / (kmax – kmin )* N è il numero di chiavi
nell’intervallo v1 - v2 nell’ipotesi di chiave numerica e
distribuzione uniforme dei valori
caso migliore per ricerca chiave successiva: quando
non si ha bisogno di nuovi accessi perchè la pagina
che la contiene è già in memoria
caso peggiore: quando si cerca la chiave seguente una
chiave in radice perché sarà in una foglia quindi si
devono compiere h-1 nuovi accessi al disco
Inserimento in B-tree di una chiave
• verifica se la chiave da inserire non è giá
presente: la ricerca termina ad un nodo foglia in
cui verrà fatto l’inserimento
• se il nodo non è completo cioè contiene meno di
m-1 chiavi allora vi si può inserire ancora una
chiave e riferimento al record
Inserimento e nodo saturo
• se la foglia è satura o completa cioè contiene m-1
chiavi, si esegue lo splitting del nodo:
– si crea un altro nodo in cui si memorizzano le chiavi >
della chiave di valore mediano oppure di posto
mediano nella sequenza (chiavi del nodo e chiave da
inserire) togliendole dal nodo originario
– la chiave di valore mediano si inserisce
ricorsivamente nel nodo padre, o meglio si inserisce
…..p’(kc,rkc) p”….
e se il padre è completo si esegue la suddivisione
(splitting) del padre e così via fino alla radice.
Inserimento in B-tree: splitting
inserisco la chiave 70
( 68+ 70+ 71+ 74+ 78 = 361) media= 72,2
..
46
..
..
..
..
..
50
..
55
..
..
60
68
..
..
65
70
66
..
..
71
..
79
..
..
..
..
..
..
..
74
..
78
..
..
..
Cancellazione da un B-tree della
chiave k
algoritmo:
P0. la chiave k da cancellare sia nel nodo n;
P1. se n è una foglia, si cancella k da n e si va a P3
P2. se n NON è una foglia si sostituisce k in n cercando tra le
chiavi ordinate dell’albero la chiave maggiore tra le minori o
quella minore tra le maggiori;
tale chiave sostitutiva di k è in una foglia, per costruzione
dell’albero, e quindi le va applicato il punto P1.
P3. controllo numero chiavi in n (foglia o nodo interno):
se m/2 -1  numero chiavi <= m-1
allora fine cancellaz.
altrimenti bisogna P4)concatenare o P5) bilanciare
Cancellazione in B-tree
cancellazione della chiave 60
46
..
..
50
..
55
..
..
60
68
..
..
65
71
..
..
..
..
66
78
..
..
..
74
..
..
..
79
..
..
..
Concatenazione processo opposto allo splitting
perché unisce due nodi in un solo nodo
num. chiavi in n = (m+1)/2 –2
Cerco un nodo q adiacente ad n nell’albero tale che
num. chiavi in q = (m+1)/2 –1
(m+1)/2 –2 + (m+1)/2 –1 = m+1-3 +1 = m - 1
“chiave tra” i due nodi nel nodo padre
Concatenazione
nodo padre: [… (kj-1, rj-1) pj-1 (kj,rj) pj (kj+1, rj+1) pj+1…]
nodo-1 da conc: [p0(k1, r1) p1 … pe-1 (ke, re) pe]
nodo-2 da conc:
[p’0(ke+1, re+1) … ]
pj-1 e pj sono puntatori ai nodi 1 e 2
i nodi 1 e 2 sono concatenati in
[p0(k1, r1) p1 … pe-1 (ke, re) pe (kj,rj) p’0(ke+1, re+1) … ]
e nel nodo padre: [… (kj-1, rj-1) pj-1 (kj+1, rj+1) pj+1…]
Cancellazione in B-tree: concatenazione
B-tree di ordine 5 per cui: 2 <=num. chiavi<=5
voglio cancellare la chiave 68
46
..
..
..
..
..
..
50
..
55
..
..
60
66
..
63
65
66
..
..
68
..
..
..
..
..
..
70
..
..
74
..
..
78
70
65
..
79
..
..
..
..
79
..
74
..
78
..
..
..
..
..
..
Cancellazione in B-tree: bilanciamento
Dati due nodi adiacenti in un B-albero bilanciamento vuol dire
ridistribuire le chiavi tra i due nodi in modo da bilanciare i nodi
medesimi:
! Ridistribuire chiavi vuol dire cambiare la chiave di “spartimento”
nel nodo padre
Cancellazione in B-tree: bilanciamento
se devo cancellare la chiave 70
..
..
..
50
50
..
..
55
55
..
..
60
..
..
..
68
70
..
..
..
..
..
..
..
65
65
..
..
68
..
71
60
..
..
..
79
71
..
..
72
..
..
..
..
..
..
..
73
..
74
..
78
..
Dalla sequenza: 50, 55, 60, 65, 68, 70 ho la sequenza: 50, 55, 60, 65, 68 distribuita:
nodo padre: 60
nodo-figlio-1: 50, 55
nodo-figlio-2: 65, 68
Struttura di un B-albero
dipende dall’ordine con cui si caricano le chiavi
e si parla di densitá di riempimento di un indice
Esercizio: costruire il B-albero di ordine m= 5, numero massimo figli,
relativo alle due sequenze di chiavi
1) 10, 15, 30, 27, 35, 40, 45, 37, 20, 50, 55, 46, 71, 66, 74, 85, 90, 79,
78, 95, 25, 81, 68, 60, 65
2) 10, 15, 20, 25, 27, 30, 35, 37, 40, 45, 46, 50, 55, 60, 65, 66, 68, 71,
74, 78, 79, 81, 85, 90, 95
Per chiavi ordinate, sequenza 2, si ottiene un B-albero con foglie di
(m+1)/2 chiavi tranne l’ultima:
in caso di caricamento di una sequenza ordinata si preferisce una
strategia di trattamento del nodo saturo a bilanciamento del fratello
a sinistra del nodo saturo fino a quando anche questo non sia saturo.
Indici e sgbd
la definizione di una chiave primaria al momento di una create table
genera automaticamente un indice B+-albero che serve a controllare la
unicitá dei valori della chiave;
la dichiarazione di una chiave esterna non crea automaticamente un
indice
Valutazione prestazioni o costi delle operazioni
ipotesi: in memoria centrale abbiamo un buffer capace di contenere
h+1 nodi, l’indice;
costo: funzione del numero di nodi da leggere e da scrivere per
operazione
B*-tree
• è una variante dei B-tree che mette tutte le
coppie (kj,rj) nei nodi foglia: nei nodi interni
rimangono le chiavi che dirigono la
navigazione sull’albero
• i nodi foglia sono poi legati in una lista
bidirezionale
• Esiste un’ulteriore variante nota con il nome
di B+-tree che differisce per i nodi interni dal
B*-tree
Esempio di B*-tree
..
25
..
..
35
..
..
..
..
..
20
..
30
..
..
25
..
40
35
..
46
..
..
..
..
50
46
..
65
..
55
..
60
..
..
..
..
..
..
..
..
..
..
65
68
..
78
..
..
..
..
..
..
..
71
80
..
..
74
85
..
..
78
90
..
..
..
Numero di Foglie in B*- tree
• Nfoglie= ((Lkey+Lrid)*Nrec)/ (Dpag * ln2),
dove Dpag*ln2 è una stima del riempimento
medio di una pagina relativa ai B*-tree, Lkey
e Lrid rispettivamente la lunghezza di una
chiave e di un riferimento in byte.
B-tree e Pagine Dati
30
..
30...
..
35
..
40
..
45
..
30
..
40…
40…
45...
30...
..
35...
Di ordinamento
(cluster)
35
..
40
..
45
..
35...
45...
Non di ordinamento
Vantaggi di
*
+
B,B ,B -tree
• Principalmente, permettono di ottimizzare le
ricerche su predicati del tipo v<X<w o range
queries
• Devono però verificarsi due condizioni, altrimenti i
costi legati all’aggiornamento del B-tree non si
giustificano:
– la ricerca non deve essere troppo estesa
– il B-tree deve usare come chiave la stessa usata per
l’ordinamento delle pagine nel file
• L’indice può essere relativo a gruppi di attributi
ovvero a chiavi complesse
Scelta dell’Organizzazione
• L’organizzazione dipende dal sgbd
• Una volta nota l’organizzazione è
necessario analizzare i suoi elementi per
poter ottenere una base dati realmente
efficiente
• L’efficienza deve generalmente essere
valutata sulla base delle applicazioni utente
che accedono alla base dati