trasparenze ppt

Le trasformazioni
•
Consideriamo un sistema termodinamico in equilibrio
– Per esempio una certa quantità di gas contenuto in un cilindro dotato di pistone
mobile
•
Pgas  Pest 
Mg
A
Supponiamo ora di alterare improvvisamente uno degli equilibri
– Quello meccanico
•
•
Il pistone sotto l’azione della pressione interna non più bilanciata da quella
esterna si metterà in moto
La presenza di attriti tra pistone e cilindro può far variare la temperatura
localmente
L’aumento della temperatura può innescare reazioni chimiche
•
L’aver alterato uno degli equilibri,
•
– porta il sistema ad evolvere attraverso stati di non equilibrio
•
(la pressione è diversa da punto a punto e sicuramente diversa da quella esterna, lo
stesso vale per la temperatura)
– verso un nuovo stato di equilibrio
•
•
Si è verificato un cambiamento di stato
Il sistema ha subito una trasformazione
G.M. - Informatica B-Automazione 2002/03
Rappresentazione di una trasformazione
nel piano PV
•
•
•
In una trasformazione che procede per stati di non equilibrio termodinamico
Siamo in grado di conoscere coordinate termodinamiche solo nello stato di
partenza (iniziale) e nello stato di arrivo (finale)
Solo questi due stati possono essere rappresentati nel diagramma PV
P
•
•
la trasformazione non può essere
rappresentata nel diagramma PV,
Negli stati intermedi non è nota la
pressione.
i
Pi
f
Pf
Vi
Vf
V
G.M. - Informatica B-Automazione 2002/03
Pgas  Pest 
Le trasformazioni quasi statiche
•
Mg
A
Una trasformazione come quella descritta nella trasparenza precedente non è
descrivibile in termodinamica
– Non passa per stati di equilibrio termodinamico!!
– Questo vuol dire che non possiamo farci dei conti sopra.
•
Dobbiamo costruirci delle trasformazioni ideali nelle quali il sistema passa
attraverso stati di equilibrio termodinamico (o comunque stati vicinissimi ad
uno stato di equilibrio termodinamico)
– Solo così potremo descrivere la trasformazione
– Ed eventualmente fare dei conti
•
Per esempio, se suddividiamo la massa M poggiata sul
pistone in tanti piccoli pesetti,
–
e togliamo un pesetto alla volta, ci saremo allontanati molto
poco dallo stato di equilibrio iniziale
– aspettiamo ora il tempo necessario perché l’equilibrio
comunque si ripristini, e poi togliamo un secondo pesetto.
– Così facendo potremo portare il sistema dallo stesso stato
iniziale allo stesso stato finale della trasformazione precedente
– Ma in questo caso durante tutta la trasformazione siamo passati
attraverso stati di equilibrio o stati molto prossimi a stati di
equilibrio, e quindi confondibili con essi.
Pi V i
Pi -P
V i +V
G.M. - Informatica B-Automazione 2002/03
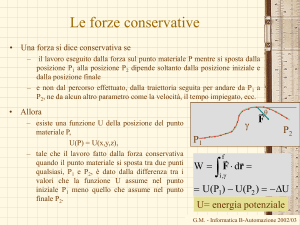
Trasformazioni reversibili
•
•
•
Trasformazione quasistatica
È una trasformazione in cui il sistema passa per stati di equilibrio
termodinamica o stati così prossimi ad uno di equilibrio termodinamico da
poter essere confusi con stati di equilibrio.
Una trasformazione quasi statica è una trasformazione ideale
Pi V i
– Richiede un tempo molto grande di esecuzione
•
Se non sono presenti effetti dissipativi,
– Lavoro effettuato da forze non conservative (forze di attrito dinamico)
– Passaggi di corrente all’interno di resistori
•
Pi -P
V i +V
Allora la trasformazione può essere percorsa all’indietro.
– Consideriamo la trasformazione quasi statica che abbiamo descritto
– Supponiamo di aver già tolto un certo numero di pesetti
– Anziché continuare a togliere i pesetti dal pistone, possiamo rimetterli ad uno ad
uno sul pistone.
– Quando li avremo rimessi tutti avremo riportato il sistema nello stato da cui
eravamo partiti
– Abbiamo cioè percorso la trasformazione all’indietro.
•
La trasformazione si dirà reversibile.
– Una trasformazione per essere reversibile deve essere quasistatica e non devono
essere presenti effetti dissipativi.
G.M. - Informatica B-Automazione 2002/03
Rappresentazione di una trasformazione
reversibile nel piano PV
•
•
•
•
In una trasformazione reversibile tutti gli stati intermedi sono di equilibrio
termodinamico
Quindi siamo in grado di conoscere le coordinate termodinamiche in tutti gli
stati intermedi
Possiamo rappresentare una trasformazione reversibile nel piano PV, mediante
una linea continua che connette lo stato iniziale con quello finale
Una trasformazione reversibile può essere suddivisa in tratti infinitesimi
P
i
Pi
Pf P
f
Vi
V
Vf
V
G.M. - Informatica B-Automazione 2002/03
Trasformazioni causate da una differenza
di temperatura
•
•
Abbiamo già accennato al fatto che alcune trasformazioni
sono causate dalla mancanza di equilibrio termico
Se la temperatura dell’ambiente esterno è diversa da quella
del sistema
– Il sistema e l’ambiente esterno interagiscono fino a
raggiungere un valore comune di temperatura (generalmente
quella dell’ambiente esterno)
– Possiamo immaginare che l’interazione è avvenuta attraverso
lo scambio di qualcosa che chiameremo calore, senza meglio
precisare cosa sia (per il momento).
– Vedremo in seguito che il calore altro non è che l’energia
scambiata tra sistema e ambiente circostante a causa della
differenza di temperatura
G.M. - Informatica B-Automazione 2002/03
La calorimetria
•
Prima che attraverso il lavoro di Joule si riuscisse a stabilire l’equivalenza tra
il calore e il lavoro meccanico,
– E quindi identificare il calore come una forma di energia
•
•
Molto pragmaticamente, i fisici avevano dato una definizione operativa del
calore.
Questa definizione parte dalla osservazione che molti sistemi termodinamici
variano la loro temperatura quando acquistano o cedono del calore.
•
•
•
Dato un sistema termodinamico a cui viene ceduto una quantità di calore Q
e subisce una variazione di temperatura T
Q
C
Si definisce capacità termica il rapporto
T
•
•
•
Naturalmente questa è la Capacità media nell’intervallo di temperatura T.
La Capacità termica è una funzione della temperatura.
Se si vuole determinare la capacità termica ad una particolare temperatura
Q
dQ
bisogna effettuare il passaggio al limite
C  lim T 0

T dT
•
Per tutti gli effetti pratici la capacità termica può essere considerata costante
per variazioni di temperatura limitate intorno alla temperatura
G.M. -ambiente.
Informatica B-Automazione 2002/03
Il calore specifico
•
•
•
•
Il calore specifico è la capacità termica riferita all’unità di massa
Consideriamo il sistema termodinamico di massa m
1 Q
A cui viene somministrato il calore Q
c
m T
Subisce una variazione di temperatura T
•
•
Il calore specifico è anche uguale alla capacità termica diviso per la massa.
Questa definizione è l’equazione fondamentale per definire il campione di
calore: la caloria
Il calore somministrato al corpo, invertendo la definizione di calore specifico
è dato da:
Q  mcT
•
•
definizione della caloria
– Si sceglie una particolare sostanza: l’acqua e le si assegna arbitrariamente calore
specifico 1
– Si prende l’unità di massa di questa sostanza: 1g
– Si prende una variazione unitaria di temperatura
•
La caloria è dunque la quantità di calore che riesce a far aumentare la
temperatura di un grammo di acqua da 14.5 °C a 15.5 °C alla pressione
atmosferica.
–
L’acqua dunque ha un calore specifico di 1 cal/(g°C) alla pressione atmosferica e a 15°C.
G.M. - Informatica B-Automazione 2002/03
Tabella dei calori specifici
•
•
Anche i calori specifici come la capacità termica dipendono dalla temperatura
Comunque per piccole variazione della temperatura nell’intorno della
temperatura ambiente possono essere considerati costanti.
•
Il calore specifico dell'acqua
diminuisce tra zero e 35°C
poi cresce nuovamente;
vale 1.007 cal/g°C a 0°C e a
100 °C
.998 cal/g°C intorno a 35 °C.
varia di molto poco tra 0°C e
100°C, si può considerare
costante.
I calori specifici, dipendono
anche
dal
tipo
di
trasformazione con cui viene
ceduto il calore.
Per i solidi ed i liquidi è facile
effettuare trasformazioni a
pressione costante (pressione
atmosferica).
Per i gas vengono forniti due
valori (diversi), a pressione e a
volume costante.
•
•
•
•
•
•
•
C m olare 
1 Q
n T
G.M. - Informatica B-Automazione 2002/03
La misura del calore -il calorimetro
•
•
•
Per la misura del calore si può usare un strumento come
quello illustrato in figura
È costituito da una certa quantità di liquido, per es.
acqua, in un recipiente il tutto circondato da pareti
adiabatiche, per evitare scambi di calore con l’esterno.
Completano lo strumento
Termometro
Agitatore
– Un agitatore per far si che la temperatura diventi uniforme
nel più breve lasso di tempo
– E un termometro che misura la temperatura del liquido.
•
•
•
è necessario conoscere la capacità termica Ctotale del
liquido, recipiente, agitatore e termometro
Si misura la temperatura prima, Ti, e dopo Tf, il
trasferimento di calore
Q  C totale
Il calore scambiato sarà dato da:
Tf  Ti 
G.M. - Informatica B-Automazione 2002/03
•
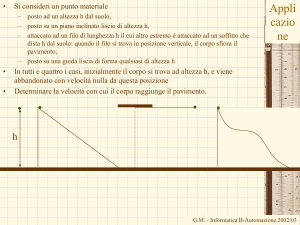
Calcolate il calore specifico di un metallo dai seguenti dati. Un contenitore fatto
di questo metallo ha una massa di 3.6kg e contiene 14 kg di acqua. Un pezzo di
1.8kg di metallo inizialmente alla temperatura di 180°C viene immerso
nell’acqua.
Il contenitore e l’acqua inizialmente hanno una temperatura di 16 °C e la
temperatura finale di tutto il sistema è 18°C.
•
•
•
•
Applic
azione
Dalla tabella dei calori specifici ricaviamo che quello
dell’acqua vale
cacqua=4190 J/ kgK
Osserviamo che il calore ceduto dal pezzo di metallo è stato tutto acquisito
dall’acqua e dal contenitore.
Il calore ceduto dal pezzo di metallo vale
•
Qc  cmTmetallo
•
Il calore acquisito dall’acqua e dal contenitore vale:
Qa  cacqua m acqua Tacqua  cm con tenito reTacqua
c acqua m acqua Tacqua  cm con tenito reTacqua  mcTmetallo
c 
cacqua m acqua Tacqua
mTmetallo  m con ten ito reTacqua

4190  14  2
117320

 412J / kgK
1.8  162  3.6  2 284.4
G.M. - Informatica B-Automazione 2002/03
Il serbatoio di calore o termostato
•
•
•
•
Con questo nome indicheremo un sistema termodinamico tale che
Può assorbire o cedere quantità anche rilevanti di calore senza che la sua
temperatura vari apprezzabilmente
Dalla definizione di capacità termica appare che un tale sistema deve avere
una capacità termica molto elevata
Q
Q Q
C 
T  
O equivalentemente una massa molto grande
T
C mc
T  0 se C  m  
•
Serbatoi di calore naturali sono gli oceani e l’atmosfera
G.M. - Informatica B-Automazione 2002/03
Trasformazioni con trasferimento di
calore ma senza aumento di temperatura
•
•
Cambiamenti di fase
Somministrando calore al sistema
– La temperatura non varia
– Varia invece la quantità di sostanza che ha cambiato fase
Q=LFm fusione
Q=Lvm evaporazione
G.M. - Informatica B-Automazione 2002/03
•
Un thermos isolato contiene 130 g di caffè caldo, alla temperatura di 80° C.
Per raffreddare il caffè aggiungete all’interno del thermos un cubetto di ghiaccio
di massa 12g tolto da una cella frigorifera alla temperatura di -10°C. Di quanti
gradi si sarà raffreddato il caffè dopo che il ghiaccio si è fuso e si sarà raggiunta
la condizione di equilibrio finale? Trattate il caffè come se fosse acqua pura e
trascurate gli scambi termici con l’ambiente circostante.
•
•
Dalla tabella dei calori specifici e da quello dei calori
latenti ricaviamo:
cacqua=4190 J/ kgK, cghiaccio=2220J/kgK, Lf=333kJ/kg
•
Il ghiaccio subirà le seguenti trasformazioni
Applic
azione
– Riscaldamento da -10°C a 0°C
Q1=mghiacciocghiaccio (Tf=0°C-Ticghiaccio)=266.4J
– Fusione a 0°C
Q2=mghiaccioLf=3996J
– Riscaldamento da 0°C alla temperatura finale Q3=mghiacciocacqua (Tf-T0°)
•
Il caffè, invece, subirà la seguente trasformazione
– Raffreddamento da 80°C alla temperatura finale Q4=mcaffècacqua (Tf-Ticaffè) (<0)
Q1  Q2  Q3  Q 4
Tf 
Q1  Q2  mghiaccioc acqua Tf  T0C   mcaffècacqua Tf  Ticaffè
m caffèc acqua Ticaffè  m ghiacciocacqua T0C  Q1  Q2
m caffèc acqua  m ghiaccioc acqua
3
130  10  4190  80  0  266.4J  3996J

 66C
3
3
G.M.
- Informatica B-Automazione 2002/03
130  10  4190  12  10  4190
Trasferimento del
calore:conduzione
•
Trasmesso dalla struttura cristallina
P
•
Q
T
 kA
t
L
k coefficiente di conducibilità termica
T2
T1
A
L
G.M. - Informatica B-Automazione 2002/03
Trasferimento del calore: convezione
•
•
Si viene a stabilire un moto, detto
convettivo, attraverso il quale le
parti di fluido più calde vengono
continuamente sostituite da parti di
fluido più fredde.
Le parti di fluido riscaldate dalla
sorgente di calore allontanandosi da
essa trasportano il calore verso la
sorgente fredda e quindi trasportano
il calore dalla sorgente più calda a
quella più fredda.
G.M. - Informatica B-Automazione 2002/03
Trasferimento del calore: irraggiamento
•
•
Non è necessario che ci sia materia tra la sorgente calda e
quella fredda.
Il trasferimento di calore avviene attraverso l’emissione e
l’assorbimento di onde elettromagnetiche
2
P= s e AT4
•
•
•
•
•
s vale 5.6x10-8 Wm-2 k-4 ed è la costante di Stefan-Boltzmann,
e è il potere emissivo della sorgente ed è un numero compreso
tra 0 e 1 che dipende dalla natura della sorgente,
A è l’area della superficie che emette la radiazione
T la sua temperatura (in kelvin).
Il potere emissivo e assume il valore limite 1 nel caso in cui la
superficie emittente è assimilabile ad un corpo nero.
1
Pass= s e ATamb4
G.M. - Informatica B-Automazione 2002/03
Una barra cilindrica di rame lunga 1.2 m e con sezione di area 4.8 cm2 è isolata
per impedire perdite di calore attraverso la sua superficie laterale. Le estremità
vengono mantenute ad una differenza di temperatura di 100°C ponendo una
estremità in una miscela di acqua e ghiaccio e l’altra in acqua bollente e vapore
Trovate quanto calore viene trasmesso nell’unità di tempo lungo la sbarra
Quanto ghiaccio si fonde nell’unità di tempo all’estremità fredda
•
•
•
•
•
Applic
azione
Dalla tabella delle conducibilità termiche e dei calori
latenti ricaviamo
krame=401W/ mK, Lf=333kJ/kg
P
Q
T
W
2 2 100 C
 kA
 401
4.8 10 m
 16.0W
t
L
mK
1.2m
Q
J
16.0
m L f
1 Q
16.0 3 kg
3 kg
s




10
 0.048  10
J
3
t
t L f t 333  10
333
s
s
kg
G.M. - Informatica B-Automazione 2002/03
Espansione isoterma reversibile
•
•
•
•
•
•
•
Per realizzare una espansione isoterma in maniera reversibile di
un certa quantità di gas contenuta in un cilindro chiusa da un
pistone mobile
Togliendo un pesetto, la pressione esterna diventa un po’ più
bassa,
il gas si espande, il suo volume diventa un po’ più grande,
durante l’espansione il gas si raffredda un poco,
assorbe pertanto un po’ di calore dal termostato per tornare alla
temperatura costante T
In tutto questo processo, se il pesetto rimosso è piccolo, il gas si
trova o in uno stato di equilibrio o in uno stato molto vicino ad
uno di equilibrio che può approssimato con uno stato di
equilibrio
Se non ci sono attriti la trasformazione può essere percorsa anche
al contrario
– Anziché togliere i pesetti, si rimettono ad uno ad uno sul pistone
Pi V i

Pi -P
V i +V

P
i
Stati di equilibrio
termodinamico
f
Stati che differiscono da uno stato
equilibrio termodinamico per un
infinitesimo
V
G.M. - Informatica B-Automazione 2002/03
Riscaldamento di un sistema
termodinamico
•
i
Per portare un sistema termodinamico
– Nella figura è illustrato il caso di una certa quantità di gas contenuto
in volume costante
•
•
•
•
Dalla temperatura Ti alla temperatura Tf, con Tf>Ti
Basterà far interagire il sistema termodinamico , il gas, attraverso
una parete conduttrice, con un termostato a temperatura Tf e
attendere un certo tempo perché il gas si porti nello stato di
equilibrio finale.
Questa trasformazione non è reversibile, perché durante tutta la
trasformazione non c’è equilibrio termico tra il sistema
termodinamico, il gas, e l’ambiente esterno, il serbatoio di calore a
temperatura Tf
Per realizzarla in maniera reversibile bisogna procurarsi un numero
molto grande di serbatoi di calore con temperatura compresa tra Ti
e Tf, in modo che la differenza di temperatura tra due serbatoi
successivi sia molto bassa.
Q
f
G.M. - Informatica B-Automazione 2002/03
Riscaldamento reversibile di un sistema
termodinamico
•
i
•
•
i
i
Q
 i+dT
•
•
•
Partendo dalla temperatura Ti, si mette a contatto il
serbatoio a temperatura Ti+dT, si aspetta che sia fluito il
calore
dQ=nCV dT
così il gas si porta alla temperatura Ti+ dT
Si mette in contatto il successivo termostato, si aspetta che
il calore sia fluito dal serbatoio al gas che raggiunge la
temperatura del secondo serbatoio
E così via
Il sistema si trova sempre in equilibrio o in stati molto
prossimi ad uno stato di equilibrio
Naturalmente si può ripercorre all’indietro.
f
Q
f
 nC dT  nC  dT 
v
i
v
i
 nC vTi  nC v Tf  Ti   nC v T
f
…………….
G.M. - Informatica B-Automazione 2002/03