Document

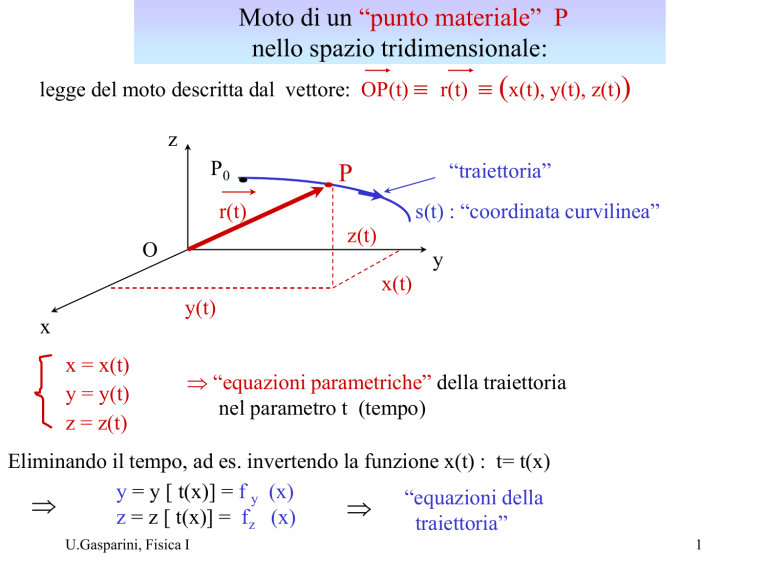
Moto di un “punto materiale” P
nello spazio tridimensionale:
legge del moto descritta dal vettore: OP(t) r(t) (x(t), y(t), z(t))
z
P0
“traiettoria”
P
s(t) : “coordinata curvilinea”
r(t)
z(t)
O
y
x(t)
y(t)
x
x = x(t)
y = y(t)
z = z(t)
 “equazioni parametriche” della traiettoria
nel parametro t (tempo)
Eliminando il tempo, ad es. invertendo la funzione x(t) : t= t(x)
y = y [ t(x)] = f y (x)
“equazioni della


z = z [ t(x)] = fz (x)
traiettoria”
U.Gasparini, Fisica I
1
Vettore velocità :




dr
(
t
)
r
(
t


t
)

r
(
t
)

r

v (t ) 
 lim
 lim
dt
t
t 0
t 0 t
r(t)
r
r (t+ t)
O
La velocità é un vettore tangente alla traiettoria :
P(t + t)
s(t)
r
dr
P(t)
r  dr = ds uT
t  0
versore tangente



dr
ds 
v (t ) 

uT  v (t )uT
dt
dt
U.Gasparini, Fisica I
2
velocità scalare
Componenti cartesiane del vettore velocità

 dx(t ) dy (t ) dz (t ) 
v  (v x , v y , v z )  
,
,

dt
dt
dt






d
(
x
(
t
)
u

y
(
t
)
u

z
(
t
)
u
 dr (t )
x
y
z)
Infatti:
v


dt
dt



dx(t )  dy (t )  dz (t ) 

ux 
uy 
u z  v x (t )u x  v y (t )u y  v z (t )u z
dt
dt
dt
Se è nota la funzione (vettoriale) velocità, la legge del moto r(t) si ottiene per
integrazione :
t
 
dr  v (t )dt 



r  r ( t )  r ( to ) 


dr 


v ( t ' ) dt '
to
t
v
x ( t )  x ( to ) 



r ( t )  r ( to ) 
t


v ( t ' ) dt '

( t ' ) dt '
y
( t ' ) dt '
to
t
y ( t )  y ( to ) 
to
U.Gasparini, Fisica I
x
v
to
t
z ( t )  z ( to ) 
v
to
z
( t ' )3dt '
Vettore accelerazione

2

dv ( t )
d r (t )
a (t ) 

dt
dt 2
L’accelerazione ha una componente tangente ed una componente normale
alla traiettoria :



dv (t )
d [v (t )uT (t )]
a (t ) 


aT
dt
dt

dv (t ) 
duT (t )
a

uT  v (t )
dt
dt
(raggio di
v (t ) 
aN
uN
curvatura)

C
“centro di
a = aT uT + aN uN
curvatura”
dv (t )
a
(
t
)

accelerazione tangente :
T
dt
accelerazione normale : a N (t ) 
U.Gasparini, Fisica I
v 2 (t )

4
Accelerazione normale
df
uT (t+dt)
uT (t)
ds = df
df
Il modulo del versore u T è costante:
2


d (uT )  2uT  duT  0
p/2
uT (t)
Il modulo del vettore d u T
è uguale a d F= ds / 
uT (t+dt)
In definitiva:
U.Gasparini, Fisica I
il vettore d u T
è normale al versore uT
ds

duT = d f uN
df


duT uT

duT
df 
1 ds 
v (t ) 

uN 
u 
u
dt
dt
 dt N
5 N
Componenti cartesiane dell’ accelerazione
 d 2 x (t ) d 2 y (t ) d 2 z(t ) 


a  (a x , a y , a z )  
,
,
2
2
2
dt
dt
 dt

Infatti:




 dv (t ) d (v x (t )u x  v y (t )u y  v z (t )uz )
a


dt
dt
dv x (t )  dv y (t )  dv z (t ) 

ux 
uy 
uz 
dt
dt
dt
d  dx (t )  
d  dy (t )  
d  dz (t )  
 
 ux   
 uy   
 uz 





dt dt
dt dt
dt dt 
d 2 x (t )  d 2 y (t )  d 2 z (t ) 

ux 
uy 
uz 
2
2
2
dt
dt
dt



 a x ( t ) u x  a y ( t ) u y  a z ( t ) uz
U.Gasparini, Fisica I
6
coordinata curvilinea
s(t)=R (t)
Esempio: moto circolare uniforme
velocità con modulo costante:
y
traiettoria
v 
ds(t )
d (t )
 R
 R
dt
dt
v(t) = R u (t)T

uT  (  sin  ,cos )
s(t)=R (t)

uN 
 (  cos  , sin  )
(t)
x (t )  R cos (t )
y (t )  R sin  (t )


 
P
R
O
“velocità angolare”:
d (t )
dt
 (t )   0  t
x

dx ( t )
d
v x (t ) 
  R sin  ( t )
  R sin  ( t )
dt
dt
dy ( t )
d
v y (t ) 
 R cos ( t )
 R cos (t )
dt
dt

v (t )  (v x (t ), v y (t ))  R (  sin  (t ), cos (t ))



v (t )  RuT (t )  vuT (t )
U.Gasparini, Fisica I

uT
7
Moto circolare uniforme (II)
v(t) = R u (t)T

uN 
(  cos , sin  )
O
(t)

uT  (  sin  , cos )
P
R
s(t)
v x (t )   R sin  (t )
x
v y (t )  R cos  (t )
dv x ( t )
d
  R cos  ( t )
  R 2 cos  ( t )
dt
dt
dv y ( t )
d
a y (t ) 
  R sin  ( t )
  R 2 sin  ( t )
dt
dt
a x (t ) 

a ( t )  ( a x ( t ), a y ( t ))  R 2 (  cos  ( t ), sin  ( t ))
U.Gasparini, Fisica I

v2 
2 
a (t )  R u N (t ) 
u N (t )
R

uN
8
Integrazione della velocità
Invertendo la relazione che definisce l’accelerazione e integrando :


dv  a (t )dt




 v  v ( t )  v ( to ) 


dv 
t


a ( t ' ) dt '
to
t
v x ( t )  v x ( to ) 


v ( t )  v ( to ) 
t

to

a ( t ' ) dt '
a
x
( t ' ) dt '
to
t
 v y ( t )  v y ( to )   a y ( t ' ) dt '
to
t
v z ( t )  v z ( to ) 
a
z
( t ' ) dt '
to
U.Gasparini, Fisica I
9
Moto con accelerazione costante:
moto di un “grave”
a = g , vettore costante


v (t )  v0 
t




gdt '  v0  g (t  t 0 )
t0
t
t


t0
t0






r (t )  r0  v (t ' )dt '  r0  [ v0  g (t ' t 0 )]dt '
1 



r (t )  r0  v0 (t  t 0 ) 
g (t  t 0 ) 2
2
v0
traiettoria
r0
g
Il moto avviene nel piano individuato dai vettori g e v0
U.Gasparini, Fisica I
10
Equazioni parametriche della traiettoria

g  (0, g ,0)

v0  (v0 x , v0 y ,0)

r0  ( x0 , y0 , z0 )
Con opportuna scelta degli assi:
x (t )  x0  v0 x t
posto t0 = 0 :



1  2
r (t )  r0  v0 t 
gt
2
y ( t )  y0  v0 y t 

z ( t )  z0
x(t)

“equazioni parametriche “
della traiettoria
x0
t
y(t)
yM
v y (t M )  v y 0  gt M  0
tM 

v y0
g
y M  y (t M )  y0  v0 y t M 
y0
z(t)
z0
1 2
gt
2
t
M
 y0 
t
v02y
g
v 02y
1

g
2
g2

t
1
gt 2
M 
2
y M  y0 
v02y
2g
Equazione della traiettoria
Equazioni parametriche equazione della traiettoria
x  x (t )
t  t ( x)
y  y(t ( x))  y( x)
y  y (t )

Scelta opportunamente l’origine degli assi
x ( t )  v0 x t
x0  0
t  x / v0 x
1
y (t )  y0  v0 y t  gt 2
2
“traiettoria” :
y ( x )  y0  v0 y

y ( x )  y0  tgx 
x
1  x 

g

v0 x
2  v0 x 
g
2
2v 0
cos2 
2
x2
y( x)
v0
angolo iniziale del vettore v0:

U.Gasparini, Fisica I
tg  v0 y / v0 x
“gittata”
xG
x
12
Gittata nel moto di un grave
Per
y0  0
y ( xG )  0.

“gittata” :


y( x) 
x
v0 x


g
 v0 y 
x
2
v


0x


g
v

x
 0y
G   0.
2
v


0x
x G  2v 0 x v 0 y
2
2v 0
cos  sin 
/ g 
g
Fissato il modulo di v0 , la gittata è funzione dell’inclinazione iniziale  ;
gittata massima :
dxG ( )
 0
d
sin 2   cos2   0
xG ( )
d (sin  cos  )
 0
d

p
4
v 02
2g
0.
U.Gasparini, Fisica I
p
p
4
2
13

Moto circolare: vettore velocità angolare 



v   r
z
p/ 2
O
v
r
y
P
(t)
x

 
d ( t )
dt
è  al piano del moto, con verso definito dalla “regola della mano destra”
Infatti:


  r  r sin
U.Gasparini, Fisica I
p
2
 r  v 
ds(t )
d (t )
r
dt
dt

 
d (t )
dt
14
Vettore accelerazione angolare 

d ( t )
 
dt

Accelerazione:

 



 dr


dv (t )
d (  r )
d
a 


 r  
dt
dt
dt
dt

 

 

a    r    (  r )

aT
moto accelerato

aN



aT    r

r



v  r





a N    (  r )



v  r

aT
moto decelerato

Componenti polari della velocità
y

ur
P
r(t)

ur2  1 costante
v

u


r(t+dt)
d

2


du
2ur  dur  0
 r 
ur dur


dur  du

ur ( t  dt )

ur (t )
x
O


r (t )  r (t )ur (t )

d 
u
dt


dur ( t )

dr ( t )
dr ( t ) 
v (t ) 

ur  r ( t )
dt
dt
dt


dr (t ) 
d (t ) 
v (t ) 
ur  r (t )
u
dt
dt

vr

v
“velocità radiale”
d (t ) 
 dr (t )

v (t )  

dt
, r (t )
dt
“velocità trasversa”
 dx (t ) dy (t ) 
,
  


 dt
dt 
U.Gasparini, Fisica I
componenti polari
16
componenti cartesiane
Componenti polari dell’ accelerazione

dv
(t )
d  dr 
d  


a 

u r
u  

dt
dt  dt r
dt


d 2r 
dr dur
dr d 
d 2 
d du

ur 

u  r
u  r
dt dt
dt dt
dt
dt
dt 2
dt 2

d 
u
dt
 
 2

d 
ur
dt
dr d 
u
dt dt
2
 d 2r
 dr d
d 2  
 d   

 u
 
a 
ur   2
r
 dt 2  r 

2


dt
dt 
 dt dt



ar
“accelerazione radiale”
In un moto circolare ( r = costante) :
 d
ar  r 
 dt
d 2
a  r
dt 2



2
 r 2  a N
 r
d
 r  a T
dt

a
“accelerazione trasversa”


uT  u


u N  ur
Composizione dei moti
1) moto circolare uniforme:
sovrapposizione di due moti armonici sfasati di p/2
e di uguale pulsazione lungo due assi ortogonali
x (t )  R cost  R sin(t  p / 2)
equazioni parametriche

y (t )  R sin(t )
della traiettoria
x(t)
t
y(t)
T/2
y
T
t
la pulsazione del moto
armonico è la velocità
angolare del moto
circolare
t=T/4
t=T/2
(t)=  t
R
U.Gasparini, Fisica I
t=0.
x
18
Esempi di composizione dei moti
2) moto di una “cicloide”
composizione di un moto circolare uniforme di raggio R
con velocità angolare  e di un moto traslatorio con
velocità v = R nel piano del moto circolare
x (t )  R sin t  Rt
equazioni parametriche
y (t )  R cos t  R
della traiettoria
y
C
moto del punto periferico
di una ruota in moto con
velocità costante
P
v = R
x
3) moto “elicoidale”
composizione di un moto circolare e di un moto traslatorio
con velocità v perpendicolare al piano del moto circolare
x ( t )  R sin t
z
y ( t )  R cos t
z(t )  v z t
y
U.Gasparini, Fisica I
x
19