Presentazione di PowerPoint - I@PhT

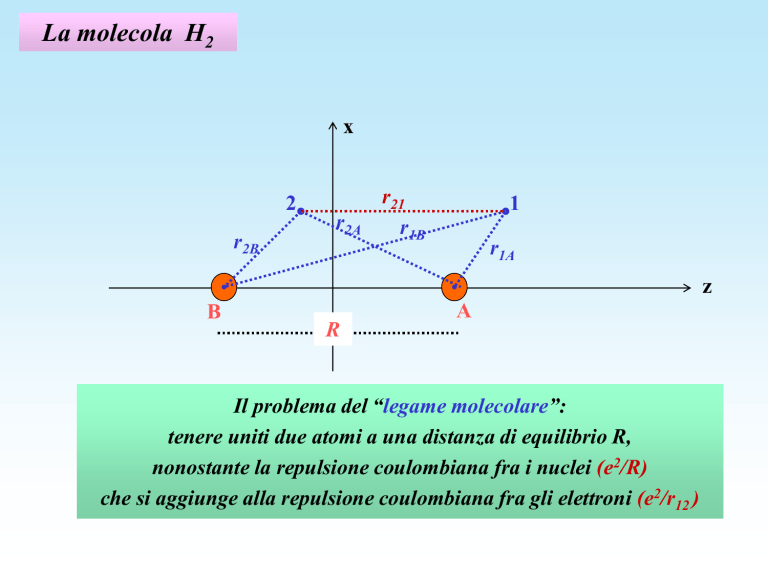
La molecola H2
x
2
r2B
r2A
r21
r1B
1
r1A
z
B
R
A
Il problema del “legame molecolare”:
tenere uniti due atomi a una distanza di equilibrio R,
nonostante la repulsione coulombiana fra i nuclei (e2/R)
che si aggiunge alla repulsione coulombiana fra gli elettroni (e2/r12 )
come si misurano
le dimensioni di una molecola
sorgente
R
un fenomeno analogo:
le “riflessioni” dei colori sul CD
i2
occhio
li3
la differenza fra i cammini
d2
d12= li2 - li1 + ld2- ld1
interferenza costruttiva per
d12= 
k
ld4
li4
ld2
ld3
li1
h
li2
ld1
a2
d34= li4 - li3 + ld4- ld3
interferenza costruttiva per
d34= 
a2+p
a4
A
a4+p
metodo della “somma sui cammini” di Feynman: contribuiscono tutti i cammini che non sono “proibiti”
(“QED, la strana teoria della luce”- per una versione didattica si veda http://www.iapht.unito.it/qm)
l i 2 li1 

h 2  a 22  h 2  a 2  p 2
calcolo del passo p fra i solchi
h 2  a 22  h 2  a 22  2a 2 p
sorgente

a 2 p 

l i 2  l i 2 1 
 sen  i 2 p
2 

li 2 

l d 2 l d1   sen  d 2 p
occhio
inserendo i dati della figura
per il blu (  450 nm): k
d12= li2 - li1 + ld2- ld1
 p |sen i2- sen d2|  0.3 p
i4  50o
i2  20o
d2  45o
d2 
ld4
li3
15o
li4
ld2
ld3
h
li2
ld1
per il rosso (  650 nm):
d34= li4 - li3 + ld4- ld3
a2
 p |sen i4 - sen d4|  0.4 p
a2+p
a4
p  1,2 m
li1
A
a4+p
nel caso della molecola ...
d12= l2 - l1  R sen 2
l3
interferenza costruttiva per
d12=   R sen 2
l4
R
sorgente
RÅ

l1
l2
  Å

raggi X
2
rivelatore

l3
l4
l’3
l’4
R
l’2
l2
l1
l’1
tipico apparato
sperimentale
sorgente di
raggi X
campione da
esaminare
rivelatore
altre configurazioni
- asse della molecola non perpendicolare al fascio
d1
l1 = l + d1

l2 = l
R
l
l
d1 = R sin

fasci di elettroni o di neutroni
- energia cinetica di un elettrone con lunghezza d’onda  10-10 m :
2
1
 2c 
Ekin 



2
2
2



2mc
2mc
2mc
( pc )2
7
( ck )2
2
 12.56  10 eVm 
1
2




10
eV
10

 106 eV
10
m


- per un neutrone Ekin  2000 volte di meno  50 meV (energie “termiche”)
x
La molecola H2
2
r2B
r2
r12
r2A
1
r1B
r1
r1A
z
B
R
A
Hamiltoniana:
   
p2A
pB2
e2 p12
p22 e2 e2 e2 e2 e2
H ( r1, r2 , RA, RB ) 

 






2 M N 2 M N R 2me 2me r12 r1A r1B r2 A r2 B
termini che dipendono
solo dalle coordinate
dei nuclei
termini che dipendono
solo dalle coordinate
degli elettroni
termini che “mescolano” le
coordinate degli elettroni e
quelle dei nuclei
Equazione di Schrödinger:
La molecola H2
   
   
   
H ( r1, r2 , R A , RB ) ( r1, r2 , R A , RB )  E ( r1, r2 , R A , RB )
Approssimazione di Born-Oppenheimer:
data la grossa differenza fra la massa dell’elettrone e quella dei nuclei, è lecito
trascurare la variazione delle posizioni dei nuclei nella soluzione del moto degli
elettroni e risolvere l’equazione con una funzione d’onda prodotto della
funzione d’onda nucleare per una funzione d’onda elettronica con i nuclei
fermi a una distanza R.
funzione d’onda
R interviene come
funzione d’onda
elettronica con i nuclei
parametro e non come
nucleare
a distanza fissa R
variabile.
 
 
 
 
 ( r1, r2 , R A , RB )   R ( r1, r2 )  ( R A , RB )
energia degli elettroni con
i nuclei fissi a una
distanza R (non
necessariamente uguale a
quella di equilibrio)
 
   
R  
H ( r1, r2 , RA , RB )  H el ( r1, r2 )  H nucl ( RA , RB )
 
 
R  
R
H el ( r1, r2 )  R ( r1, r2 )  Eel  R ( r1, r2 )
x
molecola ione-idrogeno
rB
2
2
2

p
e
e
H elR (r ) 
 
2me rA rB
B
potenziale coulombiano
repulsione fra i
due nuclei
20
10
0
energia (eV)
-10
-20
-30
elettrone-nuclei
-40
-50
-60
-70
-80
-8
-7
-6
-5
-4
-3
-2
-1
0
1
z (angstrom)
2
R
3
4
5
6
7
8
r rA
A
z
La funzione d’onda molecolare |g> è scritta come
sovrapposizione lineare di funzioni d’onda che risolvono
l’equazione di Schroedinger per l’atomo isolato:
funzioni
funzione
d’onda


1
d’onda
g 
1s(rA )  1s(rB )
atomiche
2
molecolare
Metodo LCAO:
Linear
Combination
of
Atomic
Orbitals
2
 p 2 e2 e2 



e

 1s ( rA )  E1s 1s ( rA ) 


1s ( rA )
 2m rA rB 
rB


 p 2 e2 e2 



e2




1s ( rB )  E1s 1s( rB ) 
1s( rB )
 2m rA rB 
rA


2
2
 p 2 e2 e2  





e
e

   1s( rA )  1s( rB )  E1s 1s( rA )  1s( rB ) 
1s( rA ) 
1s( rB )
 2m rA rB 
rB
rA


termine di
energia atomica
termini che si aggiungono
grazie all’attrazione da
parte “dell’altro nucleo”
1   x 2  y 2 ( z  z A )2 / ao
 x 2  y 2 ( z  z B ) 2 / ao 
1s 
e

 g (r ) 
e


2

tutte le funzioni sono mostrate
per valori
1s - sigma
geradefissi, diversi da 0, di x e y
5
x
1sg(z)
4
rB
funzione d'onda
4
1s(z-zA)
1s(z-zB)
3
B
R
r rA
A
3
2
molecola ioneidrogeno:
funzione d’onda
“gerade”
2
1
1
0
-7
-6
-5
-4
-3
-2
-1 0 1
2
z (angstrom)
3
4
5
6
7
z
H 
 g | H | g
energia della
funzione d’onda “gerade”
 g | g

 p 2 e2 e2


1
 g H  g  1s( rA )  1s( rB )
  1s( rA )  1s( rB )
2
2m rA rB
 p 2 e2 e2






1s( rA )
  1s( rA )  1s( rB )  E1s 1s( rA ) 1s( rA )  1s( rB )  1s( rA )
2m rA rB


e2
1s( rA )  1s( rA )
rB

e2
1s( rB )
rA
 p 2 e2 e2





 e2

 e2

1s( rB )
  1s( rA )  1s( rB )  E1s 1s( rB ) 1s( rA )  1s( rB )  1s( rB )
1s( rA )  1s( rB )
1s( rB )
2m rA rB
rB
rA

 p 2 e2 e2






1s(rA )  1s(rB )
  1s(rA )  1s(rB )  E1s 1s(rA )  1s (rB ) 1s (rA )  1s(rB )
2m rA rB
energia
coulombiana
2
  e2
e



  1s (rA ) 1s (rA )  1s(rB ) 1s(rB )
rB
rA





energia di
risonanza
2
  e2
e



 2 1s(rA ) 1s(rB )  1s(rA ) 1s(rB )
rB
rA





energia della funzione d’onda “gerade”
termini coulombiani
C
 g H  g  E1s  g  g
1 
 e2

 e2

  1s (rA )
1s (rA )  1s (rB )
1s (rB )
2
rB
rA
2
2

e
e




  1s (rB )
1s (rA )  1s (rA )
1s (rB )
rB
rA





x
rB
Q
B
termini di “risonanza”
 e2

C  1s( rA )
1s( rA ) 
rA
 e
 e2 

Q  1s(rB ) 1s(rA )   e
rB
R
e2
 2 x 2  y 2  ( z  z A ) 2 / ao
2
2
x  y  ( z  zB )

x 2  y 2  ( z  z A ) 2  x 2  y 2  ( z  z B ) 2 / ao




2
r rA
A
z
dx dy dz
e2
x 2  y 2  ( z  zB )2
dx dy dz
energia della funzione d’onda “gerade”
Normalizzazione della
funzione d’onda:
termini di “sovrapposizione”




1
 g  g  1s( rA )  1s( rB ) 1s( rA )  1s( rB )
S
2








1
1
  1s( rA ) 1s( rA )  1s( rB ) 1s( rB )    1s( rA ) 1s( r B)  1s( rB ) 1s( rA )
2
2

1


S  1s( rB ) 1s( rA ) 

<g| g> = 1 + S
 x 2  y 2  ( z  z A ) 2  x 2  y 2  ( z  z B ) 2  / ao

e 
dx dy dz
H
g

g H g
g g
C Q
 E1s 
1 S
da ricordare che tutti i termini (C, Q, S) sono determinati
per un certo valore della distanza interatomica R
molecola ione-idrogeno: energia della
funzione d’onda “gerade”
1sg(r)= (1s(rA)+1s(rB))/2
x
energie
10
rB
repulsione fra i
nuclei
8
somma
6
energia (eV)
4
B
0
z
R
distanza di
equilibrio,
Ro1,06 Å
2
r rA
A
livello energetico dell’atomo
isolato (R = infinito)
-2
attrazione
coulombiana da parte
alla distanza di equilibrio:
dell’altro nucleo
-4
-6
-8
energia di risonanza
H
-10
0,0
1,0
2,0
3,0
distanza fra nuclei (angstrom)
4,0
5,0
g
e2

 E1s  2,8 eV
Ro
“legame
molecolare”
1su(r)= 1/2 (1s(rA)-1s(rB))

1   x 2  y 2 ( z  z A )2 / ao
 x 2  y 2 ( z  z B )2 / ao 
e

1s u ( r ) 
e


2

x
1s - sigma ungerade
rB
8
6
1s(rA)
B
Rint
4
funzione d'onda
r rA
A
1su(r)
2
0
-2
molecola
ioneidrogeno:
funzione
d’onda
“ungerade”
-1s(rB)
-4
-6
-8
-4
-3
-2
-1
0
1
z (angstrom)
2
3
4
z
molecola ione-idrogeno: energia della
funzione d’onda “ungerade”
1su(r)= 1/2 (1s(rA)-1s(rB))
energie
x
50
rB
40
B
energia (eV)
30
repulsione fra i
nuclei
somma
0
z
Rint
20
10
r rA
A
energia di
risonanza
attrazione da parte
dell’altro nucleo
-10
-20
0,0
1,0
2,0
3,0
distanza fra nuclei (angstrom)
4,0
H
<u| u> = 1 - S
u H u
C Q

 E1s 
u u
1 S
5,0
u
1s - sigma gerade
“orbitali” molecolari
 -1s
5
4
funzione d'onda
4
3
3
2
2
1
1
0
-7
-6
-5
-4
-3
-2
-1
0
1
z (angstrom)
2
3
4
1s - sigma ungerade
8
6
funzione d'onda
4
2
0
-2
-4
-6
-8
-4
-3
-2
-1
0
1
z (angstrom)
2
3
4
5
6
7
x
r12
2
r2B
r2
La molecola H2
r2A
1
r1B
r1A
r1
z
B
A
R
2
2
2
2
2
2
2
p
p
e
e
e
e
e
p
p
e 2e
e
e
e
H  1





H  2m 2



m r
r r
r 
r
 m


r2 A r2 B r12
 ( r2
, r )   ( r )2
 m
( r )  r
1
A
 / 2 r1B
2
1
1 2
2
2
g 1
2
2
2
2
2
1A
1B
2A
2B
12
g 2
1 2
1 2
funzione d’onda:
- antisimmetrica nello scambio delle funzioni di spin
dei due elettroni,
- simmetrica nello scambio delle funzioni spaziali


 


 ( r1, r2 )   g ( r1 ) g ( r2 ) 12  12 / 2
x La molecola H
2
p12 p22 e2 e2 e2
e2 e2
H






2m 2m r1A r1B r2 A r2 B r12
H
(o )
(o )
Hm

H
,1
m,2
p12 e2 e2
(o )
H m,1 


2m r1A r1B
H m(o,1)
H m(o,)2
g
g
;
2
r2B
2
e

r12
p22 e2
e2
(o )
H m,2 


2m r2 A r2 B
B
r2
r12
r2A
1
r1B
r1A
r1
R
z
A


(o)
  g(r1 ) H m,1  g(r1 )


(o)
  g(r2 ) H m, 2  g(r2 )
2




e
(o )
(o )
H g  H m,1  H m,2   g( r1) g( r2 )
 g( r1) g( r2 )
r12
g
g
alla distanza di equilibrio
Ro  0,7 Å
H
g
e2

 2 E1s  4,7 eV
Ro
“legame molecolare”
primi livelli energetici
di molecole biatomiche
energia
orbitale molecolare
orbitale dell’atomo 1
2s
orbitale dell’atomo 2
(2)
2s u
2s
(2)
(2)
(2)
(molteplicità)
(2)
1s
(2)
(2)
2s
g
1s u
1s
g
(molteplicità)
1s
(2)
le molecole biatomiche
dall’idrogeno al berillio
legante
antilegante
l’energia di dissociazione è la
somma dell’energia elettronica,
della repulsione fra i nuclei e
dell’energia “zero vibrazionale”
2pz
“orbitali” atomici 2pz
0,15
funzione d'onda
0,10
0,05
0,00
-0,05

0
2 pz ( r )  R21 ( r )Y1 ( , )
-0,10
-0,15
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2
z (angstrom)
3
4
5
6
7
8
 Cre
 r / ao
 Cze r / ao
cos
“orbitali” molecolari  2pz
2pz - sigma gerade
0
g 2pz (r)
0

 g 2 pz ( r ) 
0
C ' [( z  z A )e rA / ao  ( z  zB )e rB / ao ]
0
0
0
2pz - sigma ungerade
0
0
0
u 2pz (r)
2pz (rA)
-2pz (rB)
0
0
0
-7
-6
-5
-4
-3
-2
-1 0
1
2
z (angstrom)
funzione d'onda
funzione d'onda
0

 u 2 pz ( r ) 
C ' [( z  z A )e
0
3
0
4
5
6
7
2pz (rB)
0
0
2pz (rA)
0
 rA / ao
 ( z  z B )e
0
 rB / ao
0
-7
-6
u 2pz (r)
]
-5
-4
-3
-2
-1 0
1
2
z (angstrom)
3
4
5
6
7
“orbitali”
molecolari
 -2pz
2pz - sigma gerade
0
g 2pz (r)
0
0
funzione d'onda
0
0
0
0
0
0
0
0
-7
-6
-5
-4
-3
-2
-1
0
1
z (angstrom)
2
3
4
5
6
2pz - sigma ungerade
0
u 2pz (r)
0
funzione d'onda
0
0
0
0
0
0
0
-7
-6
-5
-4
-3
-2
-1
0
1
z (angstrom)
2
3
4
5
6
7
7
“orbitali” atomici 2px

2 p ( r )  R21
( r )Y11( ,  )  Cre r / ao sen  ei
2px

2 p ( r )  R21 ( r )Y11( ,  )  Cre r / ao sen  e i
0,25

1
2 p ( r )  2 p ( r )   C ' xe r / ao
2 px (r ) 
2
0,20
X
0,15
funzione d'onda
andamento0,10a x>0
0,05
0,00
-0,05
-0,10
-0,15
-0,20
-0,25
andamento
a x<0
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2
z (angstrom)

2 p ( r )  R21 (r )Y11( , )  Cre r / ao sen  ei
3
4
5
6
7
8

2 p ( r )  R21 ( r )Y11( , )  Cre r / ao sen  ei



1
2 p (r )  2 p (r )  C' xer / ao
2 px ( r ) 
2
“orbitali” molecolari  2px

 u 2 px (r ) 
 rA / ao
 rB / ao
C
'
[
x
e

x
e
]
2px - pigreco ungerade
0.3
0.2
funzione d'onda
0.2
andamenti a x>0
0.1
0.1
2px (rA)
2px (rB)
0.0
2p xu(r)
-0.1
-0.1
-0.2
-0.2
andamenti a x<0
-0.3
-8 -7 -6
-5 -4 -3 -2 -1 0 1 2
z (angstrom)
3
4
5
6
7
8
“orbitali” molecolari  2px
2px - pigreco ungerade
0
0
0
funzione d'onda
0
0
andamento a x>0
0
0
0
0
0
0
-8
-7
-6
-5
-4
-3
andamento a x<0
-2
-1 0 1 2
z (angstrom)
3

 u 2 px (r ) 
C ' [ x e  rA / ao  x e  rB / ao ]
4
5
6
7
8
“orbitali” molecolari  g 2px
2px - pigreco gerade
0
0
0
funzione d'onda
0
0
andamento a x>0
0
0
0
0
0
andamento
a x<0
0
-8
-7 -6
-5
-4 -3
-2 -1 0 1 2
z (angstrom)
3
4

 g 2 px (r ) 
C'[ x e
 rA / ao
xe
 rB / ao
]
5
6
7
8
orbitale molecolare
energia
(2)
(4)
2p
(6)
(2)
Livelli
energetici
di molecole
biatomiche
2pzu
2p±
g
2pz
2p
(6)
g
(4)
2p±u
orbitale dell’atomo 1
2s
orbitale dell’atomo 2
(2)
2s u
2s
(2)
(2)
(2)
(2)
1s
(2)
(2)
2s
g
1s u
1s
g
1s
(2)
(molteplicità)
legante
legante
antilegante
molecole
biatomiche
molecole biatomiche
eteronucleari: legame ionico
attrazione fra gli ioni
repulsione fra i nuclei
e gli elettroni interni
2
e
b
E p  
R R9
nel punto di equilibrio Ro:
dE p
e
2
9b
 2  10  0
dR R
R
b
e
2
Ro8
9
2
energia nel punto di minimo:
8e
Em  
9 Ro
e 2 e 2 Ro8
E p  
R 9R 9
per Na Cl, Em -5,12 eV
(togliendo 1,42 eV di
ionizzazione si ottiene
 -3,7 eV)
molecole biatomiche
eteronucleari
energia di dissociazione:
possibili meccanismi
radiazione:
2 πc 1260 eV  nm


E
E
esempio: per O2 , E 5 eV,   240 nm
per N2 , E 7 eV,   170 nm
N2 e O2 sono “trasparenti” all’UV
UV A 380 nm > > 320 nm
UV B 320 nm > > 280 nm
UV C 280 nm > > 180 nm
UV C
UV oltre C
eccitazione non radiativa
(urti fra molecole):
distribuzione di Boltzmann:
energia di dissociazione:
possibili meccanismi
N E  Eo  e Eo / k BT
probabilità relativa di due sistemi di energie E1 ed E2:
es: N2 + O2
 2 NO
(kB= costante
di Boltzmann
 10-4 eV K-1)
P  e  ( E1  E2 ) / k BT
Ediss, N2 = -7,4 eV; Ediss, O2 = -5,1 eV
Ediss, NO = -5,3 eV; E1-E2  2 eV
a 300 K, kBT  0,03 eV  P  e-2/0,03  10-30
a 1500 K (motore Diesel), kBT  0,15 eV  P  e-2/0,15  10-6
da 1g di N2  qualche g di NO!