Nessun titolo diapositiva

•
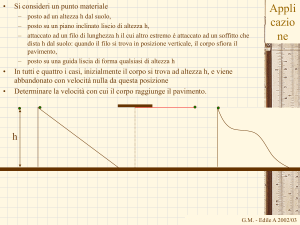
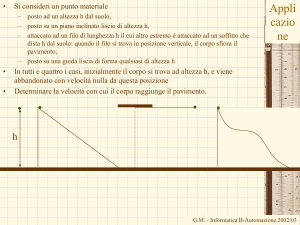
Si consideri un punto materiale
–
–
–
–
•
•
posto ad un altezza h dal suolo,
posto su un piano inclinato liscio di altezza h,
attaccato ad un filo di lunghezza h il cui altro estremo è attaccato ad un soffitto che dista h dal suolo: quando il
filo si trova in posizione verticale, il corpo sfiora il pavimento,
posto su una guida liscia di forma qualsiasi di altezza h
In tutti e quattro i casi, inizialmente il corpo si trova ad altezza h, e viene abbandonato con velocità
nulla da questa posizione
Determinare la velocità con cui il corpo raggiunge il pavimento.
Appli
cazio
ne
h
G.M. - Edile A 2002/03
•
Nel primo caso
– Agisce solo la forza peso (che è conservativa)
– Posso applicare la conservazione dell’energia
h
Appli
cazio
ne
DEm = 0 Þ Emi = Emf
EKi + EPi = EKf + EPf
EKi = 0
EPi = mgh
EKf = 12 mv 2f
EPf = 0
Abbiamo scelto il pavimento come
punto di riferimento ed assegnato
al pavimento energia potenziale
nulla
0 + mgh = 12 mv f + 0
2
v f = 2gh
L’energia potenziale iniziale viene
trasformata in energia cinetica
G.M. - Edile A 2002/03
•
Nel secondo caso agiscono
–
–
•
•
Appli
cazio
ne
Sia la forza peso, che è conservativa,
E la reazione vincolare del piano inclinato,
Solo la componente normale, perché per ipotesi il piano è liscio
Possiamo applicare la relazione lavoro energia:
DEm = Wnc Þ Wnc = WN
N
h
La normale è perpendicolare allo
spostamento: quindi il suo lavoro è nullo
P
DEm = Wnc = 0 Þ Emi = Emf
Si ritorna la caso precedente
0 + mgh = 12 mv2f + 0
EKi + EPi = EKf + EPf
EKi = 0
EPi = mgh
EKf = 12 mv 2f
v f = 2gh
EPf = 0
La velocità finale è la stessa del caso precedente
G.M. - Edile A 2002/03
•
–
–
•
Appli
cazio
ne
Nel terzo caso agiscono
Sia la forza peso, che è conservativa,
E la tensione nella corda.
Possiamo applicare la relazione lavoro energia:
h
T
DEm = Wnc Þ Wnc = WT
dWT = T× dr = 0
dr
perchè T ^ dr
P
Il lavoro infinitesimo fatto dalla tensione
DEm = Wnc = 0 Þ Emi = Emf
T è nullo, ma anche il lavoro complessivo
Si ritorna la caso precedente
0 + mgh = 12 mv2f + 0
EKi + EPi = EKf + EPf
v f = 2gh
EKi = 0
EPi = mgh
EKf = 12 mv 2f
EPf = 0
La velocità finale è la stessa del caso precedente
G.M. - Edile A 2002/03
•
Nell’ultimo caso agiscono
–
–
•
•
Appli
cazio
ne
Sia la forza peso, che è conservativa,
E la reazione vincolare della guida,
Solo la componente normale, perché per ipotesi la guida è liscia
Possiamo applicare la relazione lavoro energia:
DEm = Wnc Þ Wnc = WN
dWN = N× dr = 0
N
h
perchè N ^ dr
dr
P
Il lavoro infinitesimo fatto dalla Normale
N è nullo, ma anche il lavoro complessivo
DEm = Wnc = 0 Þ Emi = Emf
EKi + EPi = EKf + EPf
Si ritorna la caso precedente
0 + mgh = 12 mv2f + 0
v f = 2gh
EKi = 0
EPi = mgh
EKf = 12 mv 2f
EPf = 0
Conclusione: la velocità finale è sempre la
stessa in tutti e quattro i casi esaminati.
G.M. - Edile A 2002/03
•
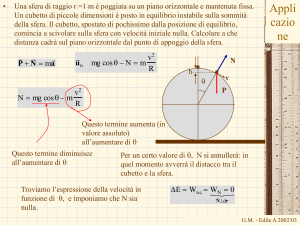
Una sfera di raggio r =1 m è poggiata su un piano orizzontale e mantenuta fissa.
Un cubetto di piccole dimensioni è posto in equilibrio instabile sulla sommità
della sfera. Il cubetto, spostato di pochissimo dalla posizione di equilibrio,
comincia a scivolare sulla sfera con velocità iniziale nulla. Calcolare a che
distanza cadrà sul piano orizzontale dal punto di appoggio della sfera.
P + N = ma
un
v2
mgcosq - N = m
R
Appli
cazio
ne
N
h
q
v
P
v2
N = mgcosq - m
R
Questo termine aumenta (in
valore assoluto)
all’aumentare di q
Questo termine diminuisce
all’aumentare di q
Per un certo valore di q, N si annullerà: in
quel momento avverrà il distacco tra il
cubetto e la sfera.
Troviamo l’espressione della velocità in
funzione di q, e imponiamo che N sia
nulla.
DEm = Wnc = WN = 0
N^dr
G.M. - Edile A 2002/03
Emf = Emi
EKf + EPf = EKi + EPi
1
2
mv2f - mgh = 0 + 0
Poniamo l’energia potenziale uguale a zero
quando il cubetto si trova alla sommità della
sfera.
h = R (1- cosq )
y
h
q
v 2 (q ) = 2gR (1- cosq )
Appli
cazio
ne
N
v
P
2gR (1- cosq )
N = mgcosq - m
= mg (3cosq - 2)
R
x
La normale N si annullerà quando
(3cosqd - 2) = 0
ossia cosq d =
Il distacco avverrà nel punto:
2
3
senq d = 1- cos2 q d = 1- 94 =
5
R = .74m
3
5
yd = R + R cosq d = R = 1.67m
3
5
9
=
5
3
xd = Rsen q d =
G.M. - Edile A 2002/03
Appli
cazio
ne
La velocità al momento del distacco
æ 2ö 2
2
v (q ) = 2gR (1- cosq ) = 2gR ç1- ÷ = gR Þ vd =
gR
è 3ø 3
3
2
Le cui componenti x e y valgono
vxd = vd cosq d =
y
h
2 2
gR = 1.70 ms
3 3
q
N
v
P
5 2
vyd = -vd senq d = gR = -1.90 ms
3 3
Il moto dopo il distacco avverrà sotto la
sola azione della forza peso (moto del
proiettile)
P = ma
x : 0 = max
y : - mg = may
L’istante in cui il cubetto impatta
al suolo si ottiene imponendo y=0.
t1 = 0.42s
t1 = -0.81s
x = xd + vxd t
y = yd + vyd t - 12 gt 2
x
Facendo ripartire il cronometro
nel momento del distacco.
yd + vyd t - 12 gt 2 = 0 t =
-vyd ± v 2yd + 2gyd
-g
x = xd + vxd t =.74 +1.70 ´.42 =1.45m
G.M. - Edile A 2002/03
•
Un blocchetto di massa m può scorrere lungo una pista, priva di attrito, a spirale
mostrata in figura.
Da quale altezza sopra il punto più basso si dovrebbe lasciar cadere il blocchetto
(con velocità iniziale nulla), per far si che riesca a fare un il giro completo del
“ricciolo”?
Quanto vale la forza complessiva agente sul blocchetto quando passa per il
punto Q della figura?
P + N = ma
un
Appli
cazio
ne
v2
mg cosq + N = m
R
v2
N = m - mgcosq
R
Affinché ci sia il contatto occorre che N sia sempre
maggiore di zero
Il punto più delicato è la sommità del ricciolo in
quanto in quella posizione
• v è minima
• Mentre il secondo termine diventa in modulo uguale a
mg
Occorre quindi imporre che N sia al massimo nulla al
vertice del ricciolo: imporre cioè che, in quella
posizione, la forza centripeta sia fornita dalla sola
forza peso
q
N
P
G.M. - Edile A 2002/03
•
Appli
cazio
ne
La velocità alla sommità del ricciolo deve quindi essere almeno:
v2
N = 0 Þ 0 = m - mg
R
Þ v 2 = gR
Imponendo la relazione lavoro-energia tra il punto di partenza, ad altezza h e la
sommità del ricciolo, si ottiene
DEm = Wnc = WN = 0
Emf = Emi
N^dr
EKf + EPf = EKi + EPi
1
2
mv2f + mg2R = 0 + mgh
v 2f = 2g ( h - 2R)
Tenendo conto del limite minimo su v, si ottiene:
gR = 2g ( h - 2R)
La velocità in Q:
R
5
+ 2R = R
2
2
5
2
1
mv
+
mgR
=
0
+
mg
R
Q
2
2
N
Þ h=
vQ2 = 5gR - 2gR = 3gR
P
P = mg
R=P=N
v2
3gR
N =m =m
= 3mg
R
R
G.M. - Edile A 2002/03
•
Due bambini stanno facendo una gara a chi riesce a centrare una scatoletta sul
pavimento con una biglia sparata da una pistola a molla, montata su un tavolo
orizzontale. Come si vede dalla figura, il bersaglio è piazzato a 2.20 m in
orizzontale dal bordo del tavolo. Orazio comprime la molla di 1.10 cm, ma il suo
tiro risulta corto di 27 cm.
Di quanto deve comprimerla Giustina per fare centro? Ignorate gli attriti.
Appli
cazio
ne
La biglia una volta rilasciata dalla molla
ed abbandonato il tavolo si muove sotto
l’azione della sola forza peso (moto del
proiettile).
Se si comincia a contare il tempo nel
momento in cui la biglia abbandona il
tavolo, le condizioni iniziali sono
xo=0,
yo=h
vxo=?
vyo=0
vxo è la velocità con cui la biglia
abbandona la molla
La legge oraria sarà:
x = vox t
1
y = h - gt 2
2
Indichiamo con Dt l’intervallo di
tempo impiegato per cadere.
Il percorso orizzontale effettuato
sarà:
d1 = vox1Dt
G.M. - Edile A 2002/03
•
Dato che il primo lancio è corto, occorre aumentare la velocità vxo affinchè la
biglia colpisca il bersaglio:
d2 = vox 2 Dt
•
Dividendo membro a membro si ottiene:
d2 vox 2
=
d1 vox1
Þ vox 2 = vox1
Appli
cazio
ne
d2
d1
La velocità vxo1 è la velocità acquistata
dalla biglia er una compressione di 1,1 cm
della molla. Quale deve essere la
compressione della molla per ottenere la
velocità vxo2 che ci consentirà di colpire il
bersaglio?
Determiniamo la relazione tra
compressione e velocità orizzontale della
biglia.
Durante l’espansione della molla, la biglia
è sottoposta alla forza elastica, alla forza
peso e alla Normale.
Le ultime due forze compiono lavoro
nullo, la forza elastica è conservativa.
Si conserva l’energia meccanca
totale
DEm = Wnc = 0
1 2 1 2
2
kx1 = mvxo1
x12 vxo1
d12
2
2
= 2 = 2
2
x2 vxo2 d2
1 2 1 2
kx2 = mvxo2
2
2
d
2.20
x2 = x1 2 =1.1cm
=1.25cm
d1
2.20 - 27.0 G.M. - Edile A 2002/03
•
Tarzan, che pesa 688 N, salta da una roccia appeso ad una provvidenziale liana
lunga 18 m (vedi figura). Dall’alto della roccia al punto più basso della sua
oscillazione cala di 3.2 m. La liana è soggetta a rompersi se la tensione supera
950 N.
Determinare se la fune si romperà
Se sì, determinare l’angolo rispetto alla verticale a cui avviene la rottura
Se no, determinare il suo valore massimo.
Appli
cazio
ne
G.M. - Edile A 2002/03
•
Appli
cazio
ne
Un blocco di legno da 0.520 kg è saldamente attaccato ad una leggerissima
molla orizzontale (k=180 N/m), ed è appoggiato su un tavolo orizzontale come
mostrato in figura.
Il blocco viene spostato in maniera da comprimere la molla di 5.0 cm e quindi
rilasciato con velocità nulla. Si osserva che il blocco supera la posizione di
equilibrio di 2.3 cm prima di fermarsi per poi tornare indietro. Determinare il
coefficiente di attrito tra il tavolo ed il blocco di legno.
sappiamo che DEm = Wnc
Emf - Emi = Wnc
i rappresenta la posizione di partenza = -0.05 m
f rappresenta la posizione di arrivo = +0.023 m
EKf + EPf - EKi - EPi = Wnc
=0
k
m
O
=0
Wnc è il lavoro fatto dalla forza di attrito dinamico
Wnc =
x1
òF
ad
· dr = -md mg(x1 - xo )
xo
G.M. - Edile A 2002/03
•
Appli
cazio
ne
Un blocco di legno da 0.520 kg è saldamente attaccato ad una leggerissima
molla orizzontale (k=180 N/m), ed è appoggiato su un tavolo orizzontale come
mostrato in figura.
Il blocco viene spostato in maniera da comprimere la molla di 5.0 cm e quindi
rilasciato con velocità nulla. Si osserva che il blocco supera la posizione di
equilibrio di 2.3 cm prima di fermarsi per poi tornare indietro. Determinare il
coefficiente di attrito tra il tavolo ed il blocco di legno.
k
m
O
1
1
EKf + kx12 - EKi - kxo2 = -m d mg ( x1 - xo )
2
2
=0
=0
md = =
k ( x12 - xo2 )
2mg ( x1 - xo )
=-
k
180
x1 + xo ) = ( 0.023+ (-0.05)) =
(
2mg
2 * 0, 520 * 9,81
180
0.027 = 0, 48
2 * 0, 520 * 9,81
G.M. - Edile A 2002/03
•
Le due masse mostrate in figura inizialmente sono poste ciascuna a 1.80 m dal
suolo e la carrucola, priva di massa e di attrito, è a 4.80 m dal suolo. Qual è
l’altezza massima raggiunta dal corpo più leggero una volta che il sistema viene
lasciato libero di muoversi?
Appli
cazio
ne
4,80 m
2,2 kg
3,2 kg
1,80 m
G.M. - Edile A 2002/03
•
•
•
Un pattinatore di massa m = 52 kg sta ruotando su una circonferenza di raggio
r=20 m ad una velocità di 3 m/s. Egli si mantiene su questa traiettoria reggendo
una fune attaccata mediante un cuscinetto privo di attrito ad un palo posto al
centro del cerchio.
Calcolare la tensione T esercitata dalla fune.
Il ghiaccio su cui egli pattina può essere considerato privo di attrito, ma per una
parte del moto attraversa una pozza sabbiosa di lunghezza 48 cm dove il
coefficiente di attrito è m = 0.10. Quanto vale la velocità subito dopo aver
attraversato la pozza sabbiosa? Quanto deve valere la tensione nella fune
affinché continui a percorrere la stessa traiettoria dopo aver attraversato la pozza
sabbiosa?
Vista dall’alto
Appli
cazio
ne
Vista laterale
G.M. - Edile A 2002/03
•
•
•
Appli
cazio
ne
Un pattinatore di massa m = 52 kg sta ruotando su una circonferenza di raggio
r=20 m ad una velocità di 3 m/s. Egli si mantiene su questa traiettoria reggendo
una fune attaccata mediante un cuscinetto privo di attrito ad un palo posto al
centro del cerchio.
Calcolare la tensione T esercitata dalla fune.
Il ghiaccio su cui egli pattina può essere considerato privo di attrito, ma per una
parte del moto attraversa una pozza sabbiosa di lunghezza 48 cm dove il
coefficiente di attrito è m = 0.10. Quanto vale la velocità subito dopo aver
attraversato la pozza sabbiosa? Quanto deve valere la tensione nella fune
affinché continui a percorrere la stessa traiettoria dopo aver attraversato la pozza
sabbiosa?
Le forse agenti
Fuori della pozza T + P + N = ma
T
nella direzione centripeta
v2
32
u n : T = man = m = 52 * = 23, 4N
r
20
Vista dall’alto
Fad
Vista laterale
N
P
G.M. - Edile A 2002/03
•
•
•
Un pattinatore di massa m = 52 kg sta ruotando su una circonferenza di raggio
r=20 m ad una velocità di 3 m/s. Egli si mantiene su questa traiettoria reggendo
una fune attaccata mediante un cuscinetto privo di attrito ad un palo posto al
centro del cerchio.
Calcolare la tensione T esercitata dalla fune.
Il ghiaccio su cui egli pattina può essere considerato privo di attrito, ma per una
parte del moto attraversa una pozza sabbiosa di lunghezza 48 cm dove il
coefficiente di attrito è m = 0.10. Quanto vale la velocità subito dopo aver
attraversato la pozza sabbiosa? Quanto deve valere la tensione nella fune
affinché continui a percorrere la stessa traiettoria dopo aver attraversato la pozza
sabbiosa?
Appli
cazio
ne
Possiamo determinare la velocità dopo la pozza
sabbiosa applicando il teorema delle forze vive.
DEK = WRisultante = WP +WN +WT +WFad
=0
La forza peso, la
normale, la tensione
fanno lavoro nullo
perché sempre
perpendicolari allo
spostamento.
=0
=0
1 2 1 2
mv f - mvi = WFad = -m d N = -m d mg
2
2
mg
T
N
v 2f = vi2 - 2m d g = 32 - 2 * 0.10 * 9,81* 0, 48 = 9 - 0, 94 = 8, 06 m 2
Vista dall’alto
s
Vista laterale P
Fad
v f = 8, 04 = 2,83 m
s
2
G.M. - Edile A 2002/03
Il diagramma dell’energia
L’energia meccanica
totale
dell’oscillatore armonico
La normale N e la forza
peso non fanno lavoro
1 2
EP = kx
2
K<0
K<0
Punti di inversione del moto
Felx dx = -dEP Felx = -
dEP
dx
Punto di equilibrio stabile
N
Fel
P
G.M. - Edile A 2002/03
La determinazione della forza
dall’energia potenziale
•
•
Nota l’espressione dell’energia potenziale possiamo determinare la forza
(direzione verso ed intensità)
Superfici equipotenziali
– Sono il luogo dei punti in cui l’energia potenziale assume lo stesso valore
• Forza peso: piani orizzontali (h=cost)
• Forza elastica: piani perpendicolari all’asse x (x=cost)
• Forza di gravitazione universale e forza di Coulomb: superfici sferiche con centro
nell’origine della forza.
•
La forza è perpendicolare alle superfici equipotenziale
– Consideriamo un qualsiasi spostamento infinitesimo su una superficie
equipotenziale (dr tangente alla superficie).
– Poiché la superficie è equipotenziale dU=0
dEP = -dW = -F × dr = 0 Þ F ^ dr
G.M. - Edile A 2002/03
La determinazione della forza
dall’energia potenziale
• Per uno spostamento che avviene lungo l’asse x:
dEP
dEP = -dW = -Fx dx Þ Fx = dx
• Per uno spostamento che avviene lungo l’asse y:
dEP
dEP = -dW = -Fy dy Þ Fy = dy
• Per uno spostamento che avviene lungo l’asse z:
dEP
dEP = -dW = -Fz dz Þ Fz = dz
F = -gradEP = -
dEP
dE
dE
u x - P uy - P uz
dx
dy
dz
Conoscere l’energia
potenziale in tutti i punti
dello spazio è equivalente
a conoscere la forza in
tutti i punti dello spazio.
La descrizione attraverso
l’energia potenziale è più
conveniente perché è
necessario conoscre un
solo valore per ciascun
punto dello spazio
anziché tre (le tre
componenti della forza)
G.M. - Edile A 2002/03
Il diagramma dell’energia
EP
Punti di equilibrio instabile
EP
Punti di equilibrio stabile
equilibrio indifferente
dEP
dx
G.M. - Edile A 2002/03
Fx = -
Il digramma dell’energia
EP
• Se l’energia meccanica totale è nulla il
punto materiale può trovarsi solo in x2
• Se l’energia meccanica ha un valore
pari ad 1 J, punto materiale oscillerà
all’intorno del punto x2, oppure sarà
fermo nel punto x4.
• Se l’energia meccanica ha un valore di 2 J, potrà oscillare all’intorno del punto x2,
oppure intorno al punto x4 (tratti marrone nella figura) a seconda della sua
posizione iniziale. Non c’è alcuna possibilità che il punto laterale possa superare
la barriera di potenziale (il valore dell’energia potenziale in x3) per passare da una
parte all’altra di x3.
• Se l’energia meccanica ha un valore leggermente maggiore di 3 J, potrà muoversi
in tutto l’intervallo rappresentato dal segmento rosa.
• Se l’energia meccanica ha un valore di 5 J, c’è un solo punto di inversione e il
punto materiale potrà allontanarsi fino a più infinito.
• Per valori dell’energia meccanica superiori alla linea 6, punto materiale può
trovarsi in qualunque posizione tra meno infinito e più infinito.
G.M. - Edile A 2002/03
Il teorema dell’impulso
• Consideriamo un punto materiale in moto rettilineo sotto
l’azione di una forza F costante
O
• xo punto di partenza
• x punto di arrivo
• L’accelerazione (costante)
• Le equazioni del moto
x = xo + vxot + 12 ax t 2
vx = vxo + ax t
x
x
xo F
Dx = x - xo
Dt = t - to = t - 0
spostamento
Tempo impiegato
F
ax =
m
mvx - mvxo = max t Þ
pxf - pxf = F ( t - 0)
ß
Dpx = FDt
G.M. - Edile-Architettura 2004/05
Generalizzazione del teorema
dell’impulso
• Dalla seconda legge della dinamica
•
Dove F è la risultante delle forze agenti sulla particella
dp = Fdt
• Per ogni intervallo infinitesimo dt
•
dp
=F
dt
Sommando su tutti gli intervalli infinitesimi (integrando tra
zero r t)
ò
t
0
dp =
ò
t
0
F dt Þ Dp =
ò
t
0
F dt
• Se la forza F è costante (modulo, direzione e verso)
• La forza F media in Dt
Dp
Fm =
=
Dt
ò
t
0
Dp = F ò dt = FDt
t
0
F dt
Dt
G.M. - Edile-Architettura 2004/05
Il prodotto vettoriale
•
Dati i vettori a e b , si definisce prodotto vettoriale
il vettore c così individuato:
– Il modulo del vettore c è dato da:
a´b
c = absen f
dove l’angolo f è l’angolo minore di 180° compreso tra i due
vettori
– La direzione è perpendicolare al piano individuato dai vettori a e b.
– Il verso è determinato con la regola della mano destra:
• I formulazione:
– Si dispone il pollice della mano destra lungo il primo vettore
– Si dispone l’indice della mano destra secondo il secondo vettore
– Il verso del medio individua il verso del prodotto vettoriale
• II formulazione
– Si chiude a pugno la mano destra mantenendo sollevato il pollice
– Si dispone la mano destra in maniera che le dita chiuse a pugno indichino il verso
in cui bisogna far ruotare il primo vettore per sovrapporlo al secondo percorrendo
l’angolo f minore di 180°
– Il verso del pollice individua il verso del prodotto vettoriale.
G.M. - Edile-Architettura 2004/05
Proprietà del prodotto vettoriale
•
Il prodotto vettoriale non è commutativo:
•
Infatti:
•
Interpretazione geometrica del prodotto vettoriale
a ´ b = -b ´ a
•
Il modulo del prodotto
vettoriale è uguale all’area
del parallelogramma formato
con u due vettori.
•
Vettori paralleli o antiparalleli
h = b sin q
b
q
a
a´b ¹ b´a
Area = ah = absinq = a ´ b
hanno un prodotto
vettoriale nullo
G.M. - Edile-Architettura 2004/05
Ulteriori proprietà del prodotto vettoriale
• Prodotto vettoriale
attraverso le componenti
cartesiane: u x u y u z
uy
uz
ux
ay
az
bx
by
bz
=
= u x ( ay bz - by az ) - u y ( ax bz - bx az ) + u z ( ax by - bx ay )
ux ´ ux = 0 ux ´ uy = uz
u x ´ u z = -u y
u y ´ u y = 0 u y ´ uz = u x
u y ´ u x = -u z
uz ´ uz = 0 uz ´ u x = u y
u z ´ u y = -u x
(
a ´ b = ax
)
a´ b+c = a´b+a´c
Proprietà distributiva
G.M. - Edile-Architettura 2004/05
Il momento di un vettore
•
Dato un vettore V qualsiasi ed il punto O, che in questa occasione si chiama
“polo”, si definisce momento del vettore V rispetto
quantità:
MO = r ´ V
y
V
q
al polo O la
r posizione rispetto ad O del punto
di applicazione del vettore V.
MO=rVsenq =V(rsenq) =bV
Il modulo del momento, MO, è uguale al
r
O
q
b=r senq
x
È importante l’ordine!
Prima r poi V!
modulo del vettore V per il braccio del
vettore V rispetto al polo O
• Il braccio è la distanza della retta di
azione del vettore V dal polo O
• Spostando il vettore V sulla sua retta di
azione il momento resta invariato.
G.M. - Edile-Architettura 2004/05
Momento della quantità di moto
o momento angolare
y
•
p
Data la particella di massa m,
– la cui posizione è individuata, al tempo t, dal
vettore posizione r,
– che al tempo t si muove con velocità v
– E quindi possiede una quantità di moto p=mv
q
•
r
Si definisce momento della quantità di moto
della particella rispetto al polo O, la grandezza:
b = r senq
x
O
O
Il modulo vale:
Le dimensioni:
O
= r´p
= rmvsenq = rmvq
[ O ] = [ r ] [ m] [ v] [senq ] = éëLMLT -1 ùû = éëML2T -1ùû
Le unità di misura:
kgm2s-1
G.M. - Edile-Architettura 2004/05
Momento della forza
– Data la particella di massa m,
y
• la cui posizione è individuata, al tempo
t, dal vettore posizione r,
• che al tempo t subisce l’azione della
forza F
q
F
b
O
– Si definisce momento della forza F
rispetto al polo O, la grandezza:
r
x
MO = r ´ F
MO = rFsenq = bF
Il modulo vale:
b = r senq = r sen(180° - q)
Le dimensioni:
[
] [
-2
2 -2
M
=
[
r
]
[
F
]
[
sen
q
]
=
LMLT
=
ML
T
[ O]
]
Le unità di misura:
kgm2s-2
Da non confondere con il lavoro che ha le stesse dimensioni
(il lavoro è uno scalare, il momento della forza un vettore: sono
due grandezze completamente diverse)
G.M. - Edile-Architettura 2004/05
Relazione tra il momento della quantità
di moto ed il momento della forza
•
Durante il moto di una particella, sia la sua posizione r che la sua velocità
cambiano con il tempo,
– È lecito aspettarsi che anche il momento della quantità di moto della particella
rispetto al polo O vari con il tempo.
– Valutiamo a quanto è uguale la sua variazione (calcoliamo la derivata):
d O d ( r ´ p) dr
dp
=
= ´p+r´
dt
dt
dt
dt
dr
´ p = v ´ p = v ´ mv
dt
•
Attenzione a non cambiare il posto dei vettori, il prodotto vettoriale non
commuta.
•
Il primo termine è nullo: i due vettori sono paralleli
d O
dp
= r´
= r ´ F = MO
dt
dt
•
La variazione del momento della quantità di moto della particella rispetto al polo O è
uguale al momento della forza applicata valutato rispetto allo stesso polo!
(è una diretta conseguenza della II legge di Newton)
G.M. - Edile-Architettura 2004/05
Forze centrali
•
Si definisce forza centrale una forza agente in una certa regione dello spazio
con le seguenti proprietà:
– per qualunque posizione del punto materiale P che subisce la forza,
– la direzione della forza agente su P passa sempre per un punto fisso dello spazio,
detto centro della forza centrale,
– e il suo modulo è funzione soltanto della distanza del punto materiale P dal centro
stesso.
•
Esempio di forza centrale: la forza di gravitazione universale.
mM
mM r
u
=
-G
r
r2
r2 r
1 q1q2
• Anche la forza di Coulomb è
F=
ur
2
4peo r
centrale
F = -G
•
Così come la forza elastica
y
F
P
r
F = -kx i
O=S
•
x
Le forze centrali sono conservative
G.M. - Edile-Architettura 2004/05
Moto di un punto materiale sotto
l’azione di una forza centrale
•
Il momento di una forza centrale valutato rispetto al centro
della forza è nullo
y
– La forza ed il vettore posizione sono paralleli o anti paralleli
d o
= Mo
dt
•
d o
=0 Þ
dt
o = costan te
Il momento della quantità di moto rispetto al centro della forza
deve rimanere costante
– in direzione
• Il moto è un moto piano
r
F
v
x
O
y
v ( t + Dt )
– Verso
• La traiettoria viene percorsa sempre nello stesso verso: orario o
antiorario
r(t + Dt)
r(t)
– Modulo
• La velocità areale è costante: il segmento che connette il centro della
forza con il punto materiale spazza aree uguali in tempi uguali .
v(t)
O
x
G.M. - Edile-Architettura 2004/05
La velocità areale
•
y
Consideriamo l’intervallo di tempo Dt
– L’area spazzata nell’intervallo Dt è quella evidenziata in figura
– Approssimativamente uguale all’area del triangolo di lati r(t),
v ( t + Dt )
r(t + Dt)
r(t+Dt), Dr.
– L’eguaglianza approssimata diventa precisa per Dt che tende a
zero.
1
DA
=
2 r(t)h
– L’area del triangolo vale:
h
v(t)
Dr
f vq
r(t)
O
vr
x
1
dA
DA
h
2 r(t)h
1
La velocità areale:
= lim Dt® 0
= lim Dt ®0
= 2 r(t)lim Dt ®0
dt
Dt
Dt
Dt
Ma: h = r ( t + Dt ) senDq
Pertanto:
h
senDq
Dq
lim Dt®0 = lim Dt®0 r ( t + Dt ) lim Dt®0
= r ( t ) lim Dt®0
= r (t )w (t )
Dt
Dt
Dt
dA 1 2
= 2 r w = 12 rvq
dt
Il modulo del momento della quantità di moto rispetto al centro della
forza vale:
e quindi: dA = 1 O
O = rmvsen f
2
dt
m
e quindi
Nel caso di forze centrali, poiché il modulo del momento della quantità di
moto è costante, allora la velocità areale è costante
G.M. - Edile-Architettura 2004/05
La velocità areale
•
Se indichiamo con Dq l’angolo formato tra i vettori posizione
y
all’istante t e t+Dt
h
r(t + Dt)sen( Dq )
v q = lim Dt ® 0 = lim Dt ®0
=
Dt
Dt
Dq
= r(t)lim Dt ®0
= rw
Dt
Il momento angolare:
Perielio
Più veloce
v ( t + Dt )
r(t + Dt)
O
h
Dq r(t)
q
v(t)
Dr
f vq
vr
x
2
=
rmvsen
q
=
mrv
=
mrr
w
=
mr
w
O
q
Afelio
Più lento
b2
e = 1- 2
a
G.M. - Edile-Architettura 2004/05
Le leggi di Keplero
•
Le orbite dei pianeti sono delle ellissi. Il sole occupa uno dei fuochi.
•
Il segmento che congiunge il pianeta con il sole, spazza aree uguali in tempi
uguali: in altre parole la velocità areale (l'area spazzata nell'unità di tempo), è
costante.
•
Il quadrato del tempo di rivoluzione (T2), è proporzionale al cubo del semiasse
maggiore dell'ellisse (a3). La costante di proporzionalità è la stessa per tutti i
pianeti del sistema solare.
•
•
L’ipotesi che la forza di gravitazione universale sia una forza centrale
insieme con quella che un sistema di riferimento legato al sole possa essere
considerato inerziale
giustifica le prime due leggi di Keplero ( in realtà la prima solo parzialmente)
•
G.M. - Edile-Architettura 2004/05
Verifica della III legge di Keplero
• Faremo la verifica supponendo che le orbite dei pianeti
siano circolari anziché ellittiche.
– L’eccentricità per la terra è 0.0167
– a è il semiasse maggiore
– b quello minore
•
•
•
b2
e = 1- 2
a
Se la traiettoria è circolare il moto è uniforme (la velocità areale deve essere
costante)
Il pianeta è soggetto ad un’accelerazione centripeta
Quindi la forza di gravitazione universale si comporterà da forza centripeta:
mM
mv 2
FG = G 2 = ma n =
r
r
G.M. - Edile-Architettura 2004/05
Verifica della III legge di Keplero
2pr
T=
v
Ma la velocità è legata al periodo dalla relazione:
2
æ 2pr ö
m
è T ø
mM mv 2
m4p2r 2 m4p 2 r
G 2 =
=
=
=
2
r
r
r
rT
T2
mM m4p2 r
G 2 =
r
T2
4p2 3
Þ T =
r
GM
2
Che appunto verifica la III legge di Keplero
G.M. - Edile-Architettura 2004/05
L’energia potenziale della forza di gravitazione
universale - la velocità di fuga
• La forza di gravitazione
universale è conservativa
U
E>0
E=0
U(r) = -G
GmMT
RT
r
mM
r
• La velocità di fuga dalla terra:
U=-
ro
E=
E<0
1 2 GmMT
mv 2
RT
• Per la fuga dalla terra, E>=0:
1 2 GmMT
2GMT
mv f = 0 Þ vf =
2
RT
RT
mg =
GmM T
R2T
Þ v f = 2gR T = 2 *9.81* 6.37 *106 = 125.0 *106 = 11.2 *103 m s
G.M. - Edile-Architettura 2004/05