Diapositiva 1 - Dipartimento di Ingegneria Industriale

Università degli studi di Padova
Dipartimento di Ingegneria Industriale
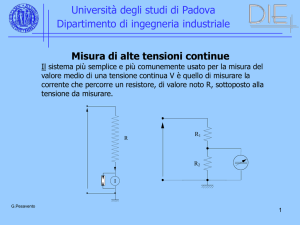
C
Rc
Rc
Rf
C
Rc
Rc
Rf
R'
C
Rc
E
G.Pesavento
Rf
1
Università degli studi di Padova
Dipartimento di Ingegneria Industriale
CONVERTITORE D’IMMAGINE
• Ottica d’ingresso
• Fotocatodo
• Griglia con funzione di otturatore
• Lenti elettrostatiche
• Sistema di deflessione del fascio
• Fosforo
• Funzionamento “ frame” e “streak”
G.Pesavento
2
Università degli studi di Padova
Dipartimento di Ingegneria Industriale
PARAMETRI PARASSITI
• Componenti e circuito hanno induttanze non
trascurabili
• La L dei componenti dipende dalle modalità
realizzative (connessioni armature dei condensatori e
struttura delle resistenze – tipologia di avvolgimento)
• Per resistori L/R minimo circa 10 ns
• L condensatori si può trovare misurando la f di
risonanza.
G.Pesavento
3
Università degli studi di Padova
Dipartimento di Ingegneria Industriale
L'induttanza L, di una spira di perimetro l, formata da un
conduttore di diametro d, con l » d, , può essere
calcolata con l'espressione
 4l

L  0, 2  l   ln  K 
 d

dove l e d sono espresse in metri e L in µH; k è una
costante che dipende dalla forma della spira e che
mediamente, in prima approssimazione, si può porre
eguale a 2,5.
G.Pesavento
4
Università degli studi di Padova
Dipartimento di Ingegneria Industriale
Si possono avere delle oscillazioni sul fronte qualora la
Rf non sia sufficiente a smorzarle.
Generalmente per contenere le oscillazioni entro il 5%
basta una
1
L


Rf
Rc
2
Cs
con Cs serie di C1 e C2 e, di fatto, circa eguale a C2.
Tenuto conto che la durata del fronte determina il
prodotto RfC2, si vede che l'induttanza può
condizionare la realizzazione di fronti troppo brevi in
quanto Rf non può essere ridotta oltre certi limiti.
G.Pesavento
5
Università degli studi di Padova
Dipartimento di Ingegneria Industriale
Capacità di una linea verso terra di diametro d
all’altezza h
2πl
C  ε
4h
ln
d
Orizzontale
G.Pesavento
2πl
C  ε
1,15l
ln
d
Verticale
6
Università degli studi di Padova
Dipartimento di Ingegneria Industriale
SG
C1
Rf
Re
L
Cc
Rc
Lc
C2
Circuito per ridurre l’ampiezza delle oscillazioni
G.Pesavento
7
Università degli studi di Padova
Dipartimento di Ingegneria Industriale
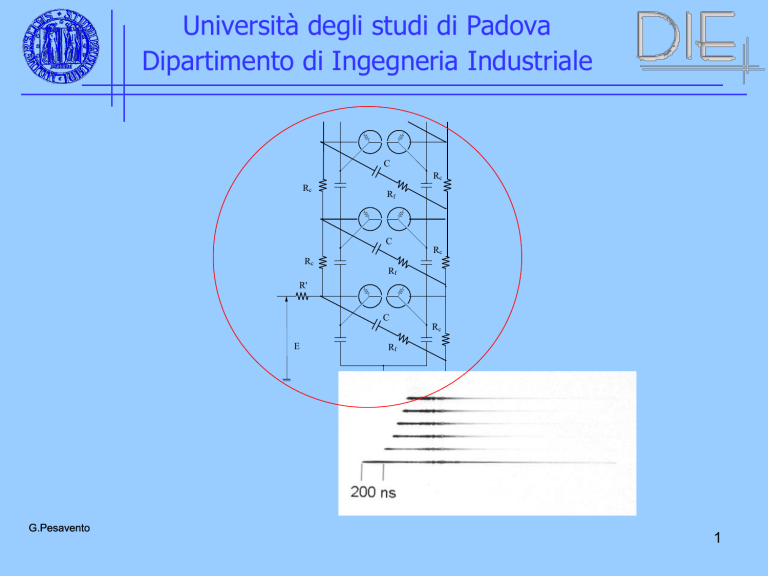
9000 pF
12 Ω
700 Ω
300 Ω
700 Ω
300 Ω
700 Ω
300 Ω
9000 pF
CT=500 pF
RT=216 Ω
18 stadi
12 Ω
9000 pF
12 Ω
9000 pF
12 Ω
MD


TG
C2
Schema di chopper per 3600 kV
G.Pesavento
8
Università degli studi di Padova
Dipartimento di Ingegneria Industriale
G.Pesavento
9
Università degli studi di Padova
Dipartimento di Ingegneria Industriale
IMPULSI OSCILLANTI
• Usati di solito per prove sul posto
• Denominati
OLI (Oscillating Lightning Impulses)
f = 15 – 500 kHz
oppure OSI (Oscillating Switching Impulses) con
f = 1 – 15 kHz.
G.Pesavento
10
Università degli studi di Padova
Dipartimento di ingegneria elettrica
G.Pesavento
11
Università degli studi di Padova
Dipartimento di ingegneria Industriale
L’andamento della tensione, trascurando le resistenze
di coda è del tipo

t 
z
C1 
2
2
v(t)= V 0
sin ω nt 1-z  
1-exp(- )  cos ω nt 1-z +
2
T 
C1+C 2 
1-z
 

T=
2L
R
ωn 
1
LC s

R
z=
2


Cs
L
Nella realtà, l’andamento sarà oscillante intorno
all’esponenziale della coda dettato da queste.
G.Pesavento
12
Università degli studi di Padova
Dipartimento di Ingegneria Industriale
Il rendimento in tensione è funzione di z e vale :
-πz 
C1 
η=
)
1+exp(
2
C1+C 2 
1-z 
Il rendimento è maggiore di 1 e quindi
l’impianto da trasportare è più piccolo e più
leggero
G.Pesavento
13
Università degli studi di Padova
Dipartimento di Ingegneria Industriale
G.Pesavento
14
Università degli studi di Padova
Dipartimento di Ingegneria Industriale
G.Pesavento
15